本博客主要分为两部分:
1、PINN模型论文解读
2、PINN模型相关总结
第一部分:PINN模型论文解读
一、摘要
基于物理信息的神经网络(Physics-informed Neural Network, 简称PINN),是一类用于解决有监督学习任务的神经网络,同时尊重由一般非线性偏微分方程描述的任何给定的物理规律。
原理:它不仅能够像传统神经网络一样学习到训练数据样本的分布规律,而且能够学习到数学方程描述的物理定律。
优势:与纯数据驱动的神经网络学习相比,PINN在训练过程中施加了物理信息约束,因而能用更少的数据样本学习到更具泛化能力的模型。
缺陷:PINN的缺点是较难处理高维数据,低维可以处理,因为所需训练数据随着方程维度的增加而呈现指数增加,故这一点很大地限制了PINN求解高维方程;PINN模型的求解速度其实是很慢的,作为“没有免费午餐”定理的一个方面,作为一种“通用方法”,与为特定偏微分方程设计的传统数值格式相比,PINN在近似偏微分方程数值解的精度和速度方面仍然处于劣势。
问题分类: 文章分为两部分, 第一部分写的是 Data-driven solutions of nonlinear partial differential equations, 就是在讲怎么解 PDEs(Partial Differential Equations), 第二部分写的是 Data-driven discovery of nonlinear partial differential equations, 就是在讲怎样解PDE的反问题 (带参数的PDE,参数需要在解的过程中求解出来)。
问题求解算法模型:根据问题的数据类型不同,设计了两种不同的问题求解算法模型,即连续时间和离散时间模型。
实验验证分析:本文对 第一部分 Data-driven solutions of nonlinear partial differential equations 选取两个方程(数据类型为连续时间和离散时间)进行PINN模型验证分析;对 第二部分 Data-driven discovery of nonlinear partial differential equations 也选取两个方程(数据类型为连续时间和离散时间)进行PINN模型验证分析
全文组织结构:
二、解决的问题
1、监督学习是机器学习中的一个大类, 很多分类问题,回归问题都可以用它来解决。 那么, 从求解PDE的角度来看, 监督学习能发挥什么样的作用呢? (如何逼近一个函数(算子)一直以来便是数学中的难题。 数学家们发展了很多工具来逼近函数, 如插值理论,框架, 谱方法 , 有限元等。 从逼近论的角度来看, 神经网络(Neural Networks)便可以看做一个非线性函数逼近器。 我们期望输出一个数据, 通过神经网络输出的值可以反应出输入数据的好坏, 有效性等, 从而有助于我们理解问题。 假设我们限制神经网络输出的值是一维的, 那么对于 binary classfication 来说, 我们可以把大于 0 的分为一类, 小于 0 的分为另一类。但是对于一个PDE来说, 我们如何来判断输入数据的好坏呢? )
2、机器学习的最新研究在众多科学学科中有了革命性的成果,但在复杂物理、生物或者工程领域中常常因为训练数据采集难度高,限制了机器学习在这些领域的发展,如何在较小训练集的情况下能够达到较高的预测精度呢?(在很多实际的工程问题中,我们经常会碰到很多预测问题,而当这些预测问题与时间和空间相关时,他们往往会与偏微分方程(PDE)相关,比如台风预报、河流流速流量预测等等。一般来说,主流的求解偏微分方程问题的手段大多采用有限元法。有限元法的基本思想是借助离散化的方法,通过将大问题进行分解,转化成可以简单求解的小问题。那么这种方法有什么缺陷呢?最明显的一个缺陷是,这个方法需要进行离散化,通过将问题区域网格化来进行求解。但是在很多实际的问题中,区域往往并非是规则的、易分的几何区域,此时网格很难生成,基于网格的方法也无法取得很好的效果。除此缺陷外,传统的求解方法还存在着噪声对解的准确性影响很大、高维问题难以求解、由已知的稀疏的观测解很难反推原问题等等。而最近机器学习等数据驱动的方法被证明在解决一些预测问题上有着比较好的效果,我们可以不需要任何物理先验知识,仅仅通过大量的数据去对结果进行预测。这个预测过程自然也绕开了偏微分方程。但是,数据驱动方法也有问题,那就是很多情况下我们无法获得足量且优质的数据。对于有些工程问题,我们进行实验获取数据的成本太高,不足以支撑我们一遍遍进行实验直到获得足够的数据;而在一些工程实践中,我们的设备精度不够,无法支撑我们获得质量足够好的数据。那么一个很自然的想法出现了——能不能将我们已知的一些物理知识和数据驱动的方法相结合呢?)
三、所提算法模型
1、算法模型总览:
模型而所谓的物理神经网络,其实就是把物理方程作为限制加入神经网络中使训练的结果满足物理规律,而这个所谓的限制是怎么实现的?其实就是通过把物理方程的迭代前后的差值加到神经网络的损失函数里面去,让物理方程也“参与”到了训练过程。这样,神经网络在训练迭代时候优化的不仅仅的网络自己的损失函数,还有物理方程每次迭代的差,使得最后训练出来的结果就满足物理规律了。
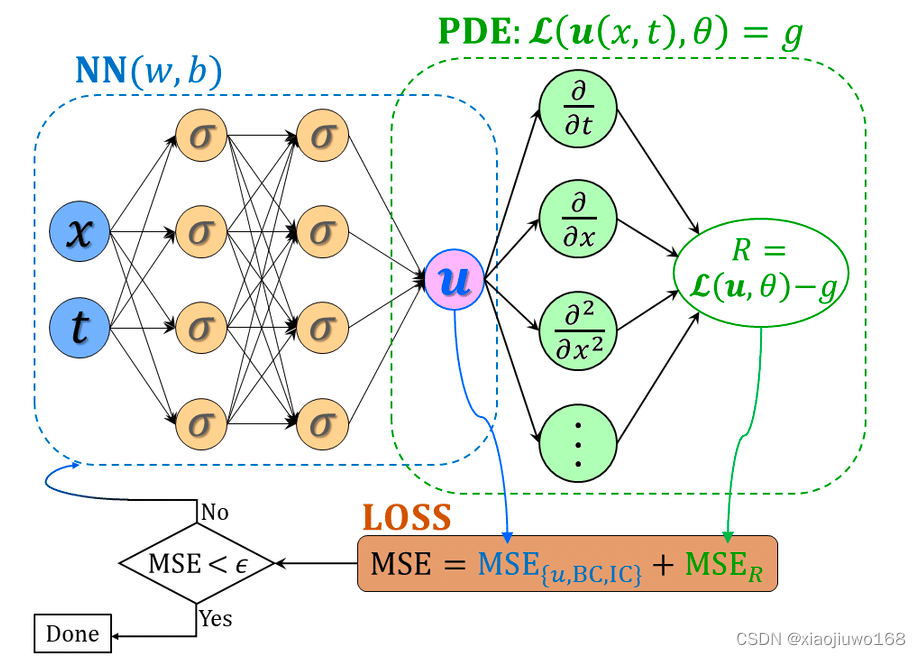
2、算法模型图解:
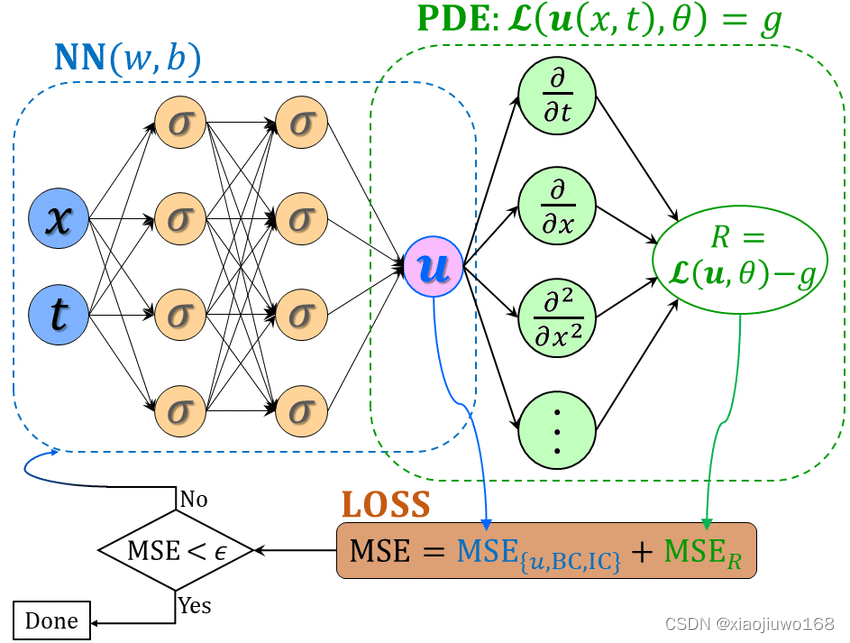
图中:MSE代表均方误差(loss约束的一种),MSE_{u,BC,IC}代表数据的拟合情况,能够像传统神经网络一样学习到训练数据样本的分布规律;MSE_R代表方程的拟合情况,能够学习到数学方程描述的物理定律。(其中u,BC,IC 分别代表微分方程的解、边界条件限制、初始条件限制)
微分方程模型:给定一个非线性PDE :
用一个具体的例子(Burgers方程,其中参数λ是已知的,故可以在具体的方程中,对应的问题是 Data-driven solutions of nonlinear partial differential equations, 就是在讲怎么解 PDEs(Partial Differential Equations))来说明。
主要的想法和步骤:
step1、初始化方程及边界条件: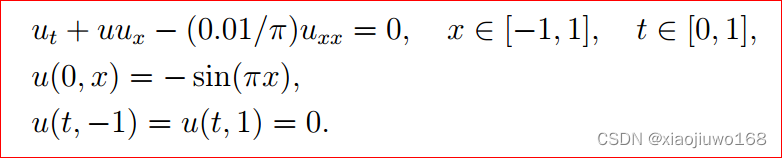
step2、利用 Neural Networks 来逼近 。
定义损失函数为: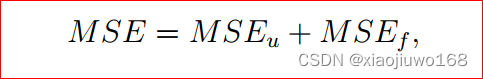
其中: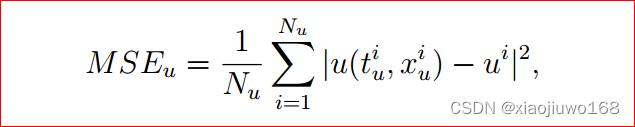
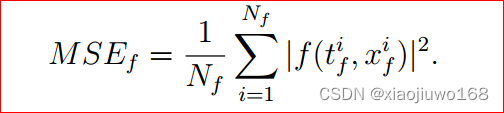
我们来分析一下损失函数。 如果神经网络能很好地求解出PDE的解, 那么对于来自初边值的任一个点, 其值MSEu趋于零;对于内部的配置点, 因为很好地拟合了微分方程, MSEf趋于零,也就是说, 损失函数的值为 0 时, 我们便可以说在训练集上每个点都有神经网络的值趋于真实值 。
这样便问题便转化为如何优化损失函数。利用神经网络的反向传播机制和L-BFGS便可以求解。
想必看这个具体的例子,应该比较能够理解其原理,没错,就是这么简单就实现了!!下面来归纳这两种模型的通用解法:
3、算法模型两类通用解法:
问题明确为:
1、Data-driven solutions of partial differential equations:参数λ已知的时候,如何求的未知的解u(x,t)
2、 Data-driven discovery of partial differential equations:参数λ 未知的时候,如何求解u(x,t)的同时确定参数λ
针对这两个问题,下面两种通用求解算法模型依据数据类型的不同均可进行处理。
3.1 连续时间模型

其实这里照着 算法模型图解 讲解部分的理解来看,已经非常清晰明了,不再进行进一步的阐述,主要在下面介绍离散时间模型的例子。
3.2 离散时间模型


到第二个离散时间模型的例子,大家可以会很疑惑,如何像连续时间模型一样构建Loss,即MSE=MSE_{u,BC,IC}+MSE_R,其实很好理解的,具体来说,之前连续时间模型的输出是一个u,而离散时间模型的输出在上面已经提到了,是一个多输出的神经网络拟合,并且构成了物理信息神经网络,有多个方程。因此,它的MSE=MSE_{u,BC,IC}(多个输出的u,像连续时间模型一样进行求和即可)+MSE_R(多个R,像连续时间模型一样进行求和即可)。
四、实验验证
1、问题明确为:Data-driven solutions of partial differential equations:参数λ已知的时候,如何求的未知的解u(x,t)
1.1 连续时间模型:
选取代表性的方程Schrodinger equation:
结果展示: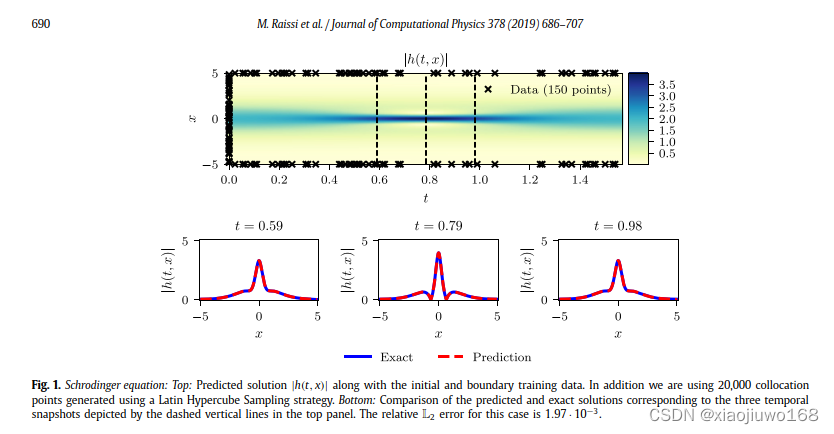
1.2 离散时间模型:
选取代表性的方程Allen-Cahnequation:

结果展示:
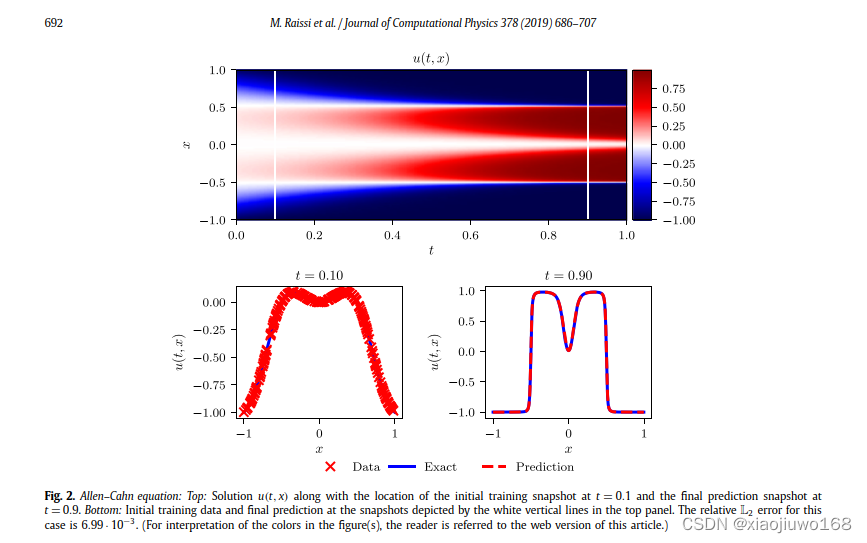
2、问题明确为:Data-driven discovery of partial differential equations:参数λ 未知的时候,如何求解u(x,t)的同时确定参数λ
2.1 连续时间模型:
选取代表性的方程Navier–Stokes equation:
结果展示: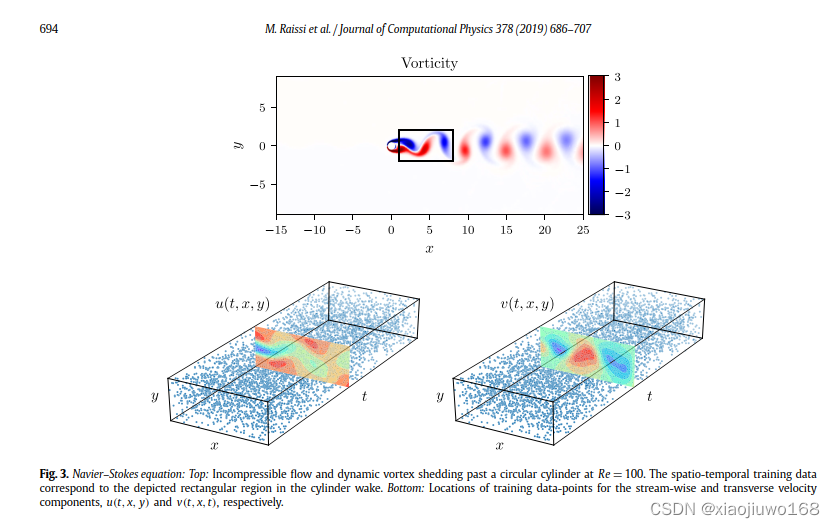
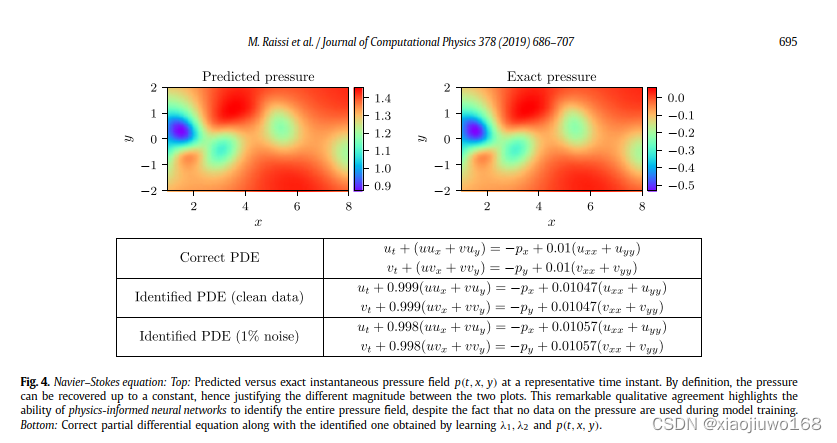
2.2 离散时间模型:
选取代表性的方程 Korteweg–de Vries equation:
结果展示: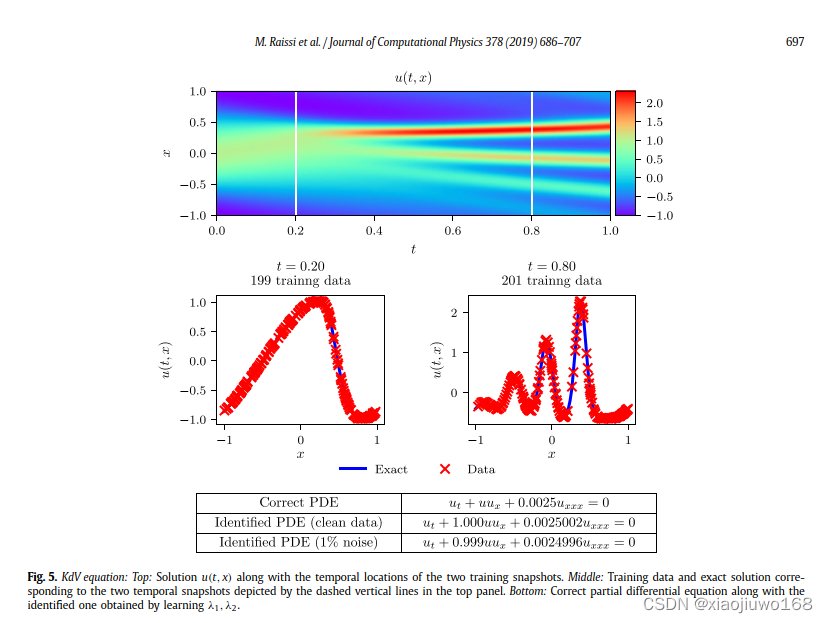
五、总结
详细内容参考原文,这篇文章的关键是:
Why?
PINN:物理信息神经网络是在神经网络通用近似理论的基础上,通过加入偏导数等算子给数值模拟加上了物理约束,从而使得整个网络具有模拟物理规则的作用。关键点在于:通用近似理论 + 物理信息的传递(导数算子+残差构建)+NN的自动微分(AD)
How?
怎么构建网络去优化?简单的全连接神经网络甚至已经能很好地进行通用近似了!!!
What?
用PINN可以做什么?解偏微分方程,在各种不同的领域中都有涉及。物理方面,其中的波动方程、程函方程、格林函数等等都是有待攻克的领域,当然也已经有很多人有了很多的发现,但是基于前人研究也会有更多的见解。
第二部分:PINN模型相关总结
完善第二部分PINN的相关总结 …,正在进行时。
参考文献:
1、方程自己解(1)——物理信息神经网络(PINN)
2、物理神经网络(PINN)解读
3、基本模型 PINNs : Physics Informed Neural Networks
4、当神经网络遇上物理: PINNs原理解析
5、内嵌物理知识神经网络(PINN)是个坑吗?
版权归原作者 xiaojiuwo168 所有, 如有侵权,请联系我们删除。