数据结构（初阶）—— 排序算法（上）

前言

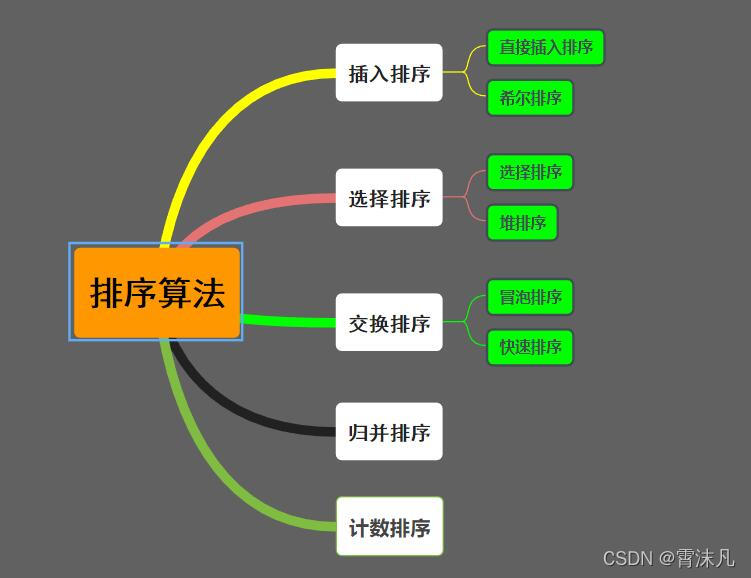
   ** 排序在我们日常生活中很常见，如：打扑克牌、商品的销量、价格、好评度等都需要用到排序；排序目的在于让我们跟容易对事物一目了然；所以掌握好排序也是非常有必要的；接下来我们介绍排序算法的前两个：插入排序和选择排序；**

一、直接插入排序

**什么是直接插入排序？ **

** 相信大家都完过扑克牌，摸得一手好牌（如果全是炸弹^-^）牌堪比人上人呀；我们从开始摸第一张牌起其后摸得所有牌，都需要插入到相应的位置，让自己手中的牌按升序或降序的排列方式组合起来；**

1.动图演示

对于一个随机组合的数组[ 6, 2, 10, 3, 9, 4, 8, 5, 1, 7 ] ,我们如何利用直接插入排序，将其排列成升序或降序的排列方式呢？

看过了动图，那么如何操作实现呢？

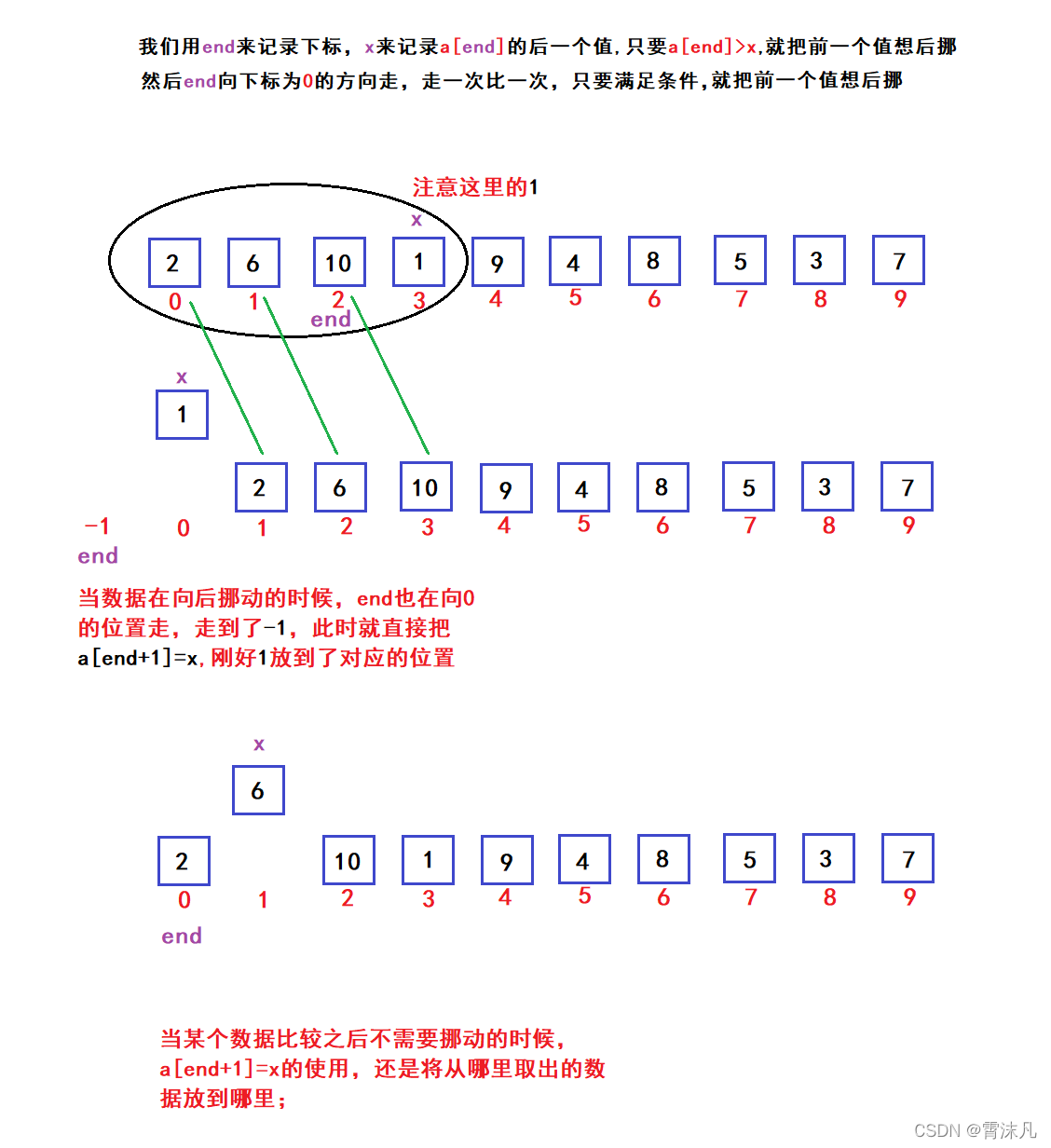
2.代码实现

// 插入排序
void InsertSort(int* a, int n)
{
    assert(a);
    for (int i = 0; i < n - 1; i++)
    {
        //将x插入【0，end】有序区间
        int end = i;
        int x = a[end + 1];
        while (end >= 0)
        {
            if (a[end] > x)
            {
                a[end + 1] = a[end];//将前一个数向后挪动
                --end;
            }
            else
            {
                break;
            }
        }
        a[end + 1] = x;
    }
}

二、希尔排序

    **希尔排序，顾名思义就是有一个叫希尔的大佬想出的排序算法；也被称为"****缩小增量排序****"它的本质还是插入排序，是在直接插入排序算法的基础上进行改进；他是如何一步一步改进的呢？**

1.希尔大佬来告诉你他是怎么想的？

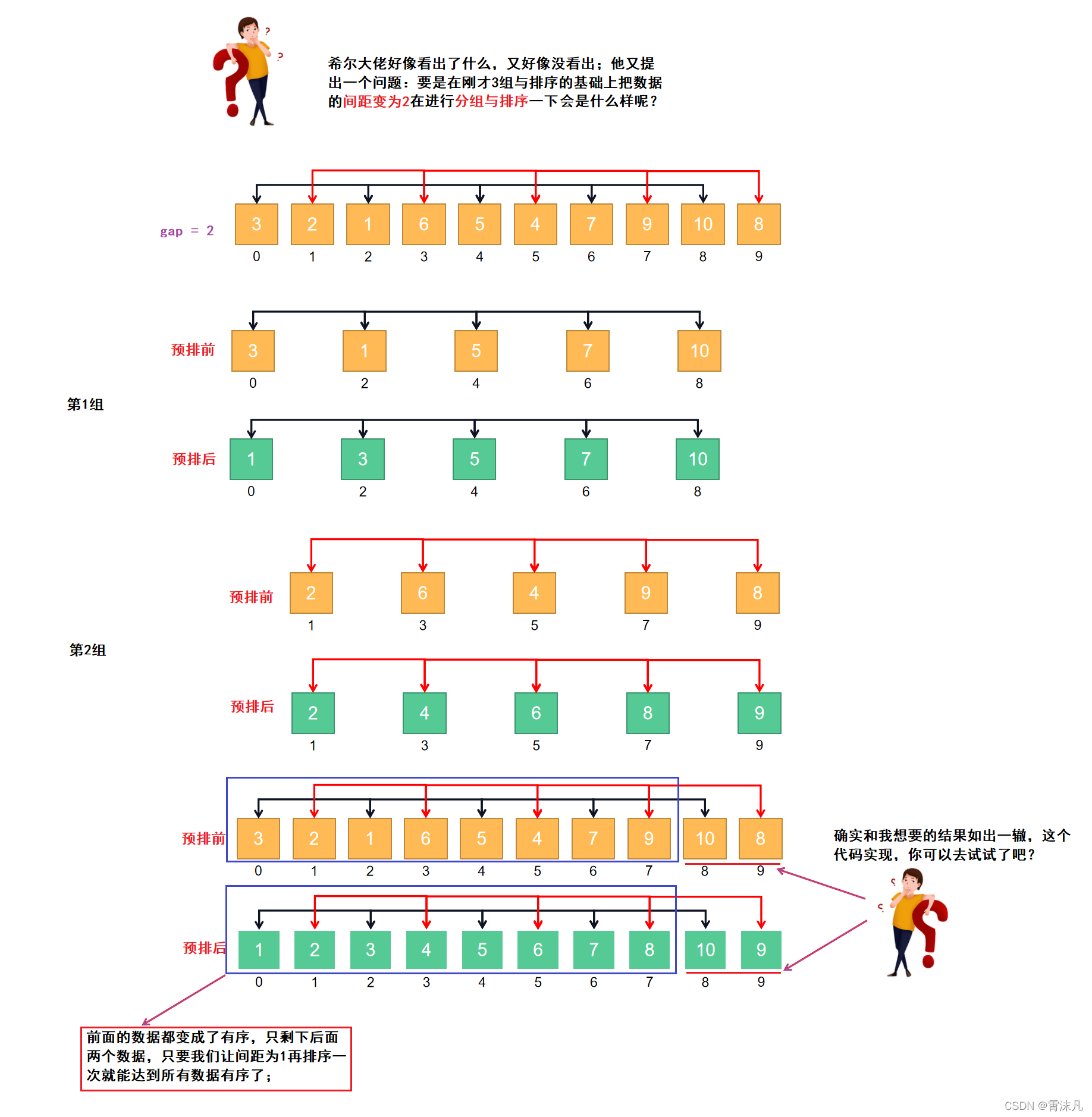
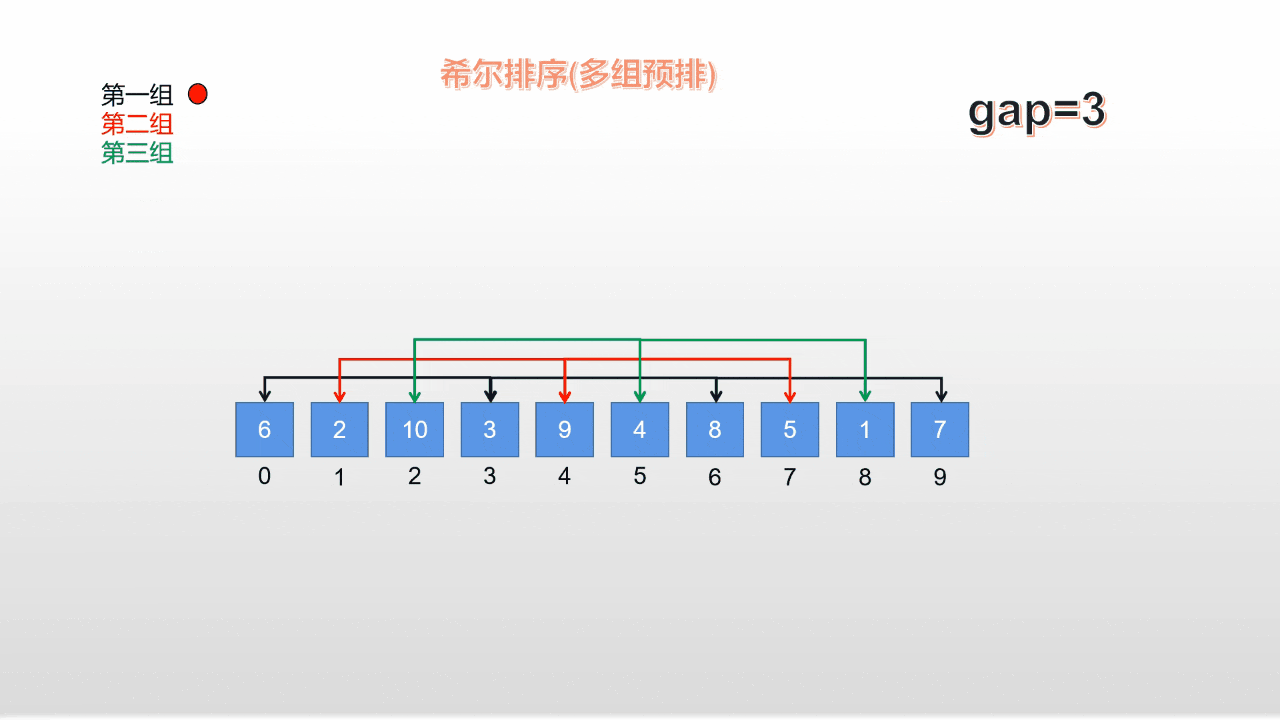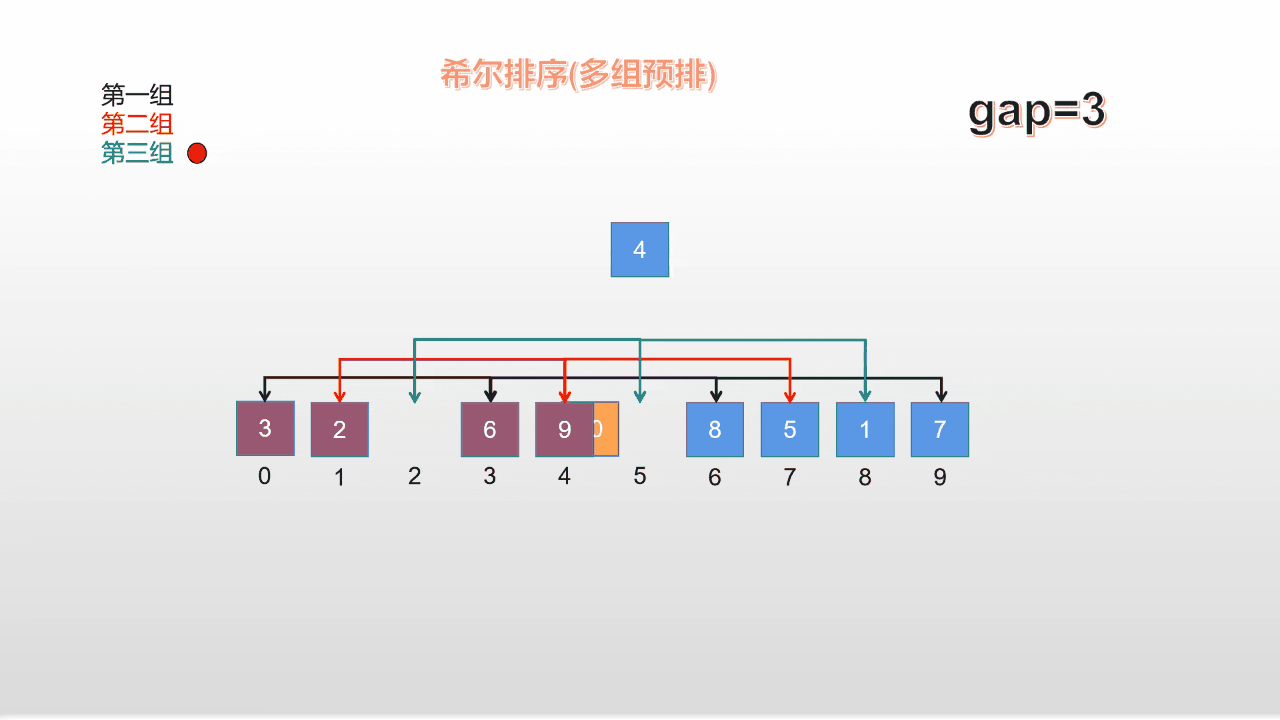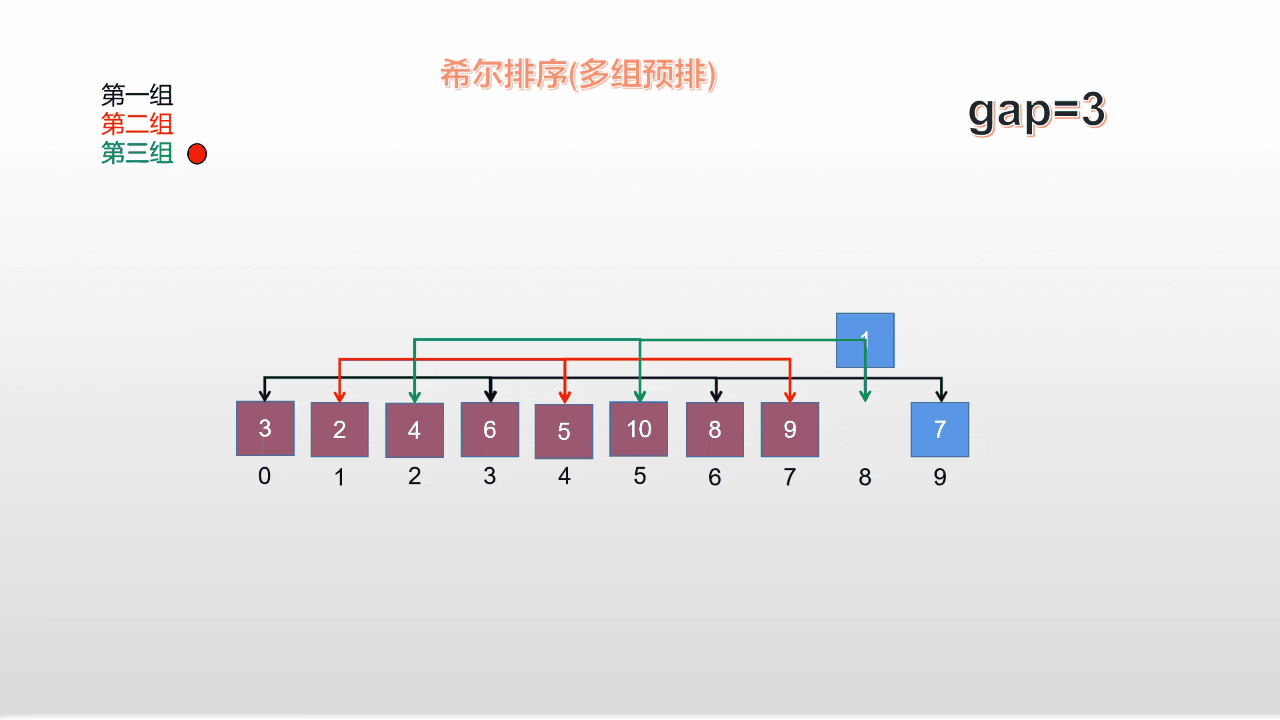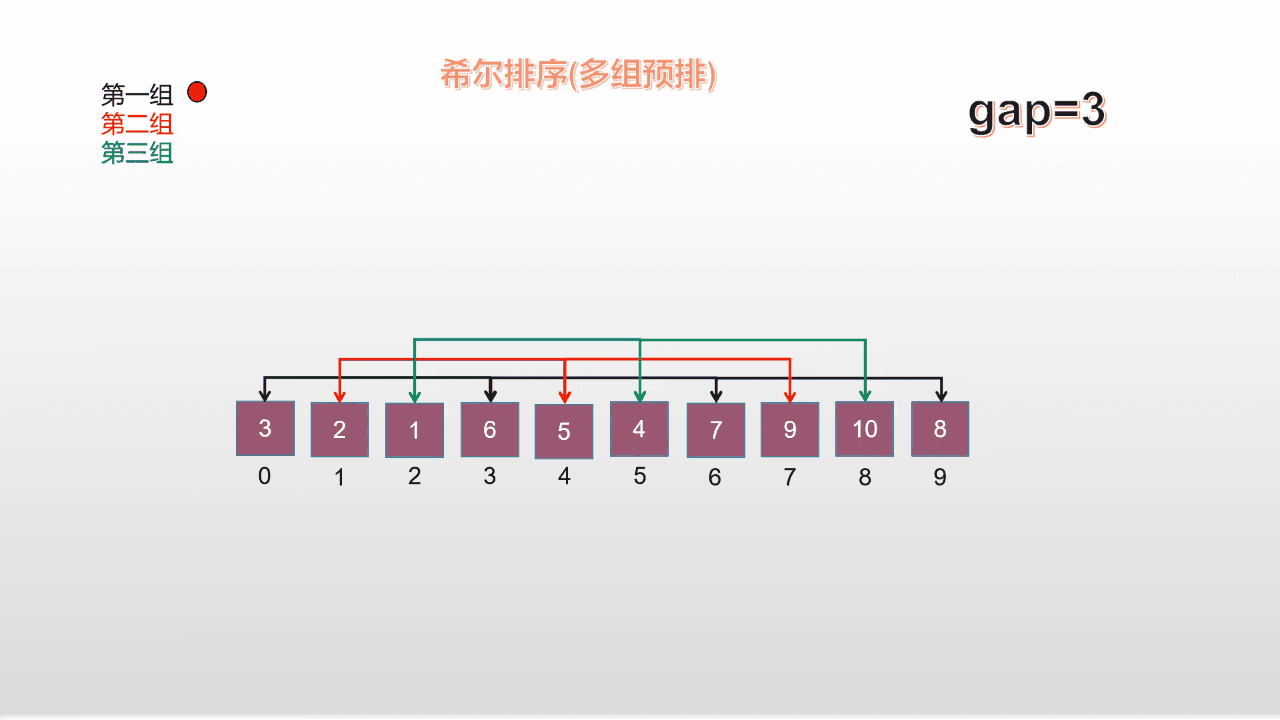
2.如何实现单趟的分组预排（含动态演示）

*我们以间距（gap*）为3为例；来对这10个数据进行第一组的与排序； **

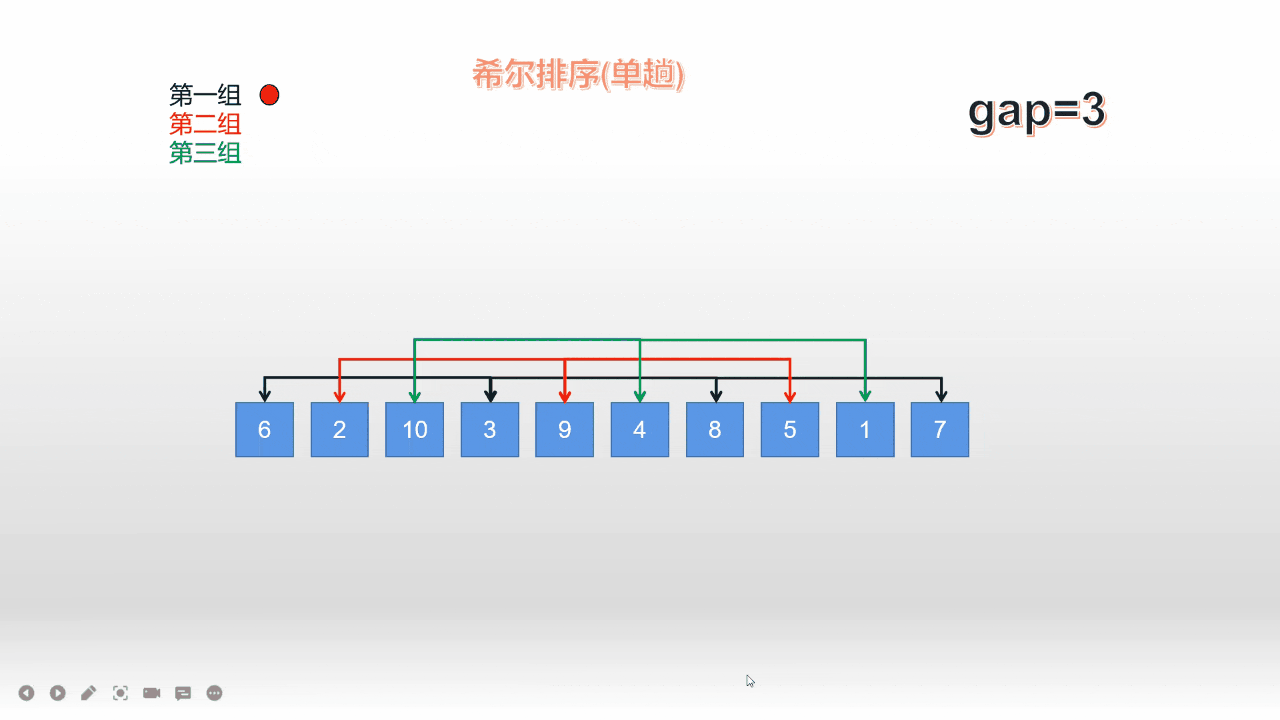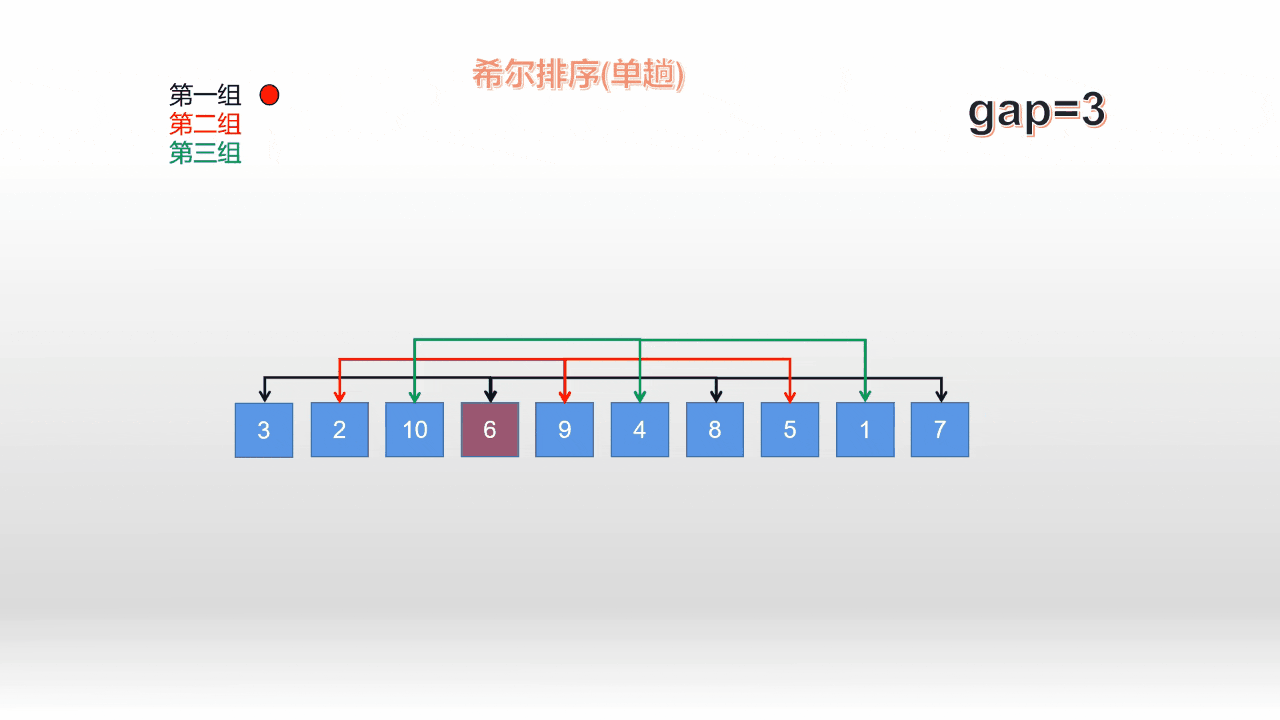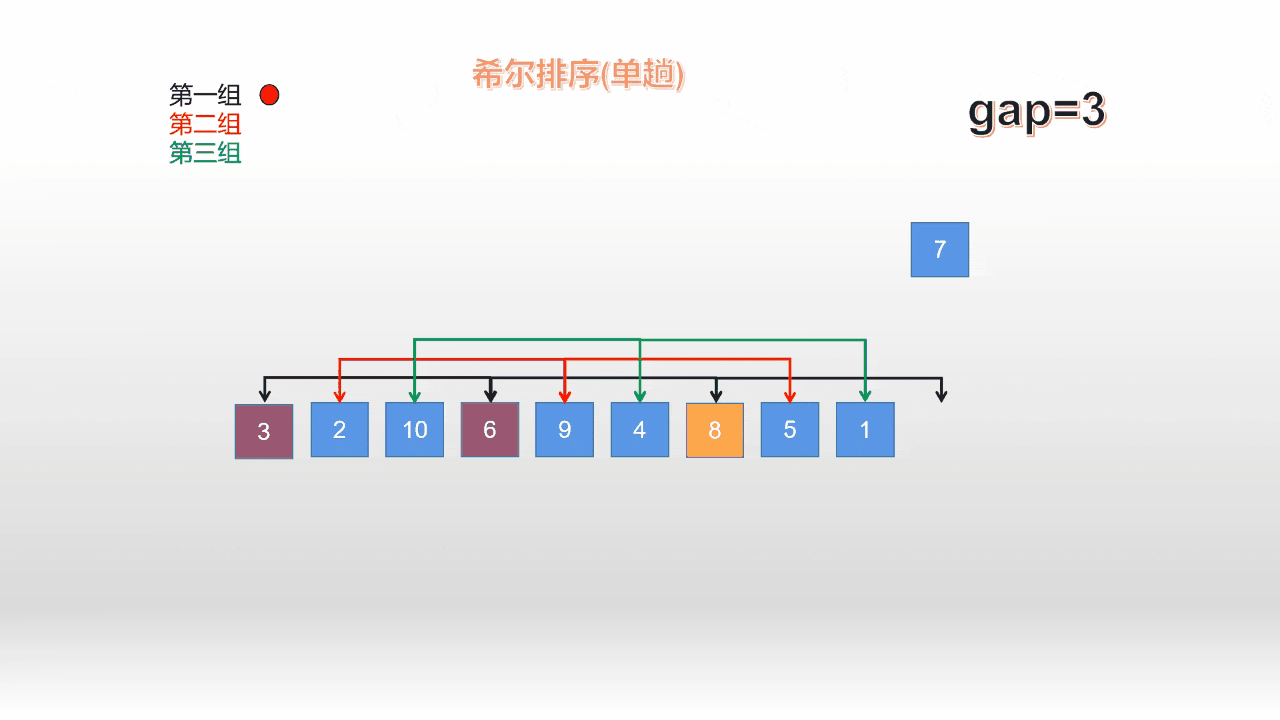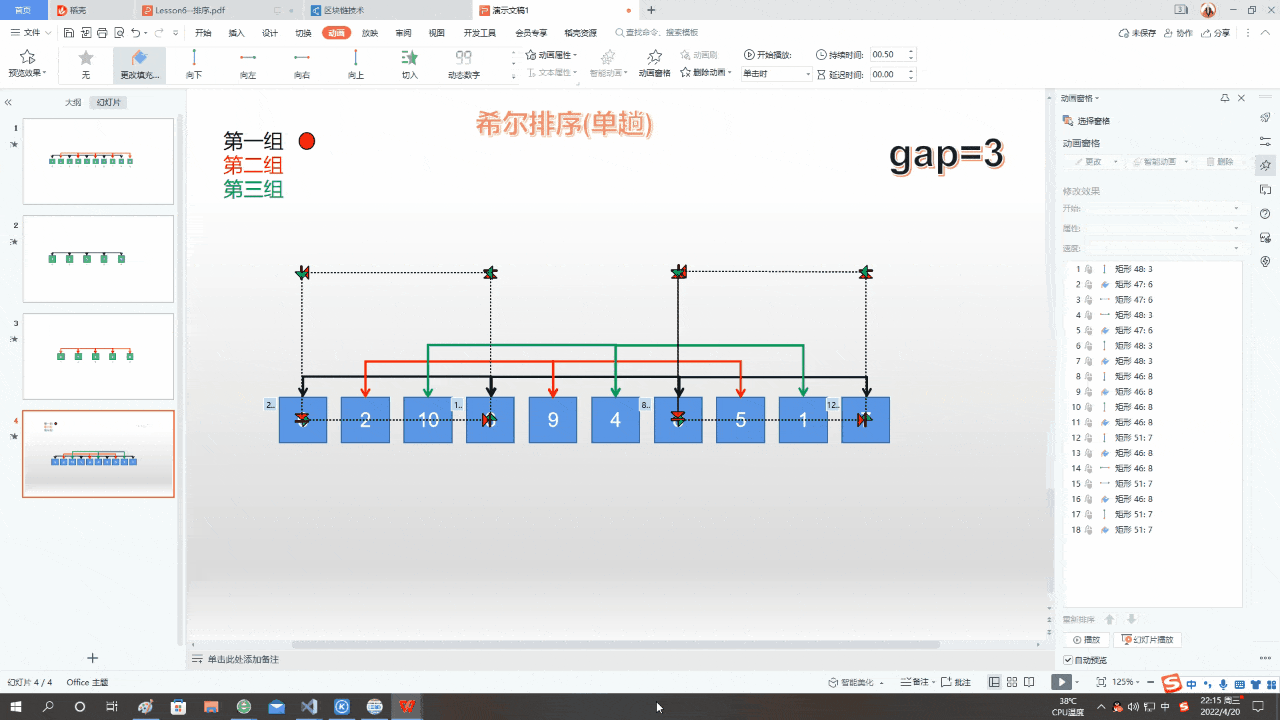
从上面的动图可以看出，本质思想还是直接插入；

void ShellSort(int* a, int n)
{ 
int gap = 3;
    for (int i = 0; i < n - gap; i+=gap)
    {
        int end = i;
        int x = a[end + gap];
        while (end >= 0)
        {
            if (a[end] > x)
            {
                a[end + gap] = a[end];
                end -= gap;
            }
            else
            {
                break;
            }
        }
        a[end + gap] = x;
    }
}

3. 多组预排序的方法（含动态演示）

方法1：

在单趟与排序的基础上外面套一层循环，一共gap组，那就循环gap次；

动图演示：

方法2：

在方法1的基础上做了一些改进，它不再是先排完第一组再排第二组，再排第三组；它让三组同时开始预排；

**动图演示： **

上述两种方法都是不错的，方法2并没有质的提升，但是在量上略微提升了一些；

代码实现

// 希尔排序
void ShellSort(int* a, int n)
{ 
    //多组一锅炖1
    int gap = 3;
    for (int j = 0; j < gap; j++)
    {
        for (int i = 0; i < n - gap; i+=gap)
        {
            int end = i;
            int x = a[end + gap];
            while (end >= 0)
            {
                if (a[end] > x)
                {
                    a[end + gap] = a[end];
                    end -= gap;
                }
                else
                {
                    break;
                }
            }
            a[end + gap] = x;
        }
    }
    //多组一锅炖2
    int gap = 3;
    for (int i = 0; i < n - gap; ++i)
    {
        int end = i;
        int x = a[end + gap];
        while (end >= 0)
        {
            if (a[end] < x)
            {
                a[end + gap] = a[end];
                end -= gap;
            }
            else
            {
                break;
            }
        }
        a[end + gap] = x;
    }
}

4. 希尔排序实现

    **从本段第一点的介绍，希尔大佬提出先将数组以间距为3分为3组数据进行预排，再以间距为2将数组分为2组进行预排；最后再以间距为1（即直接插入排序）进行最后的一次排序；达到升序或降序的排列组合；** 

// 希尔排序
void ShellSort(int* a, int n)
{
    int gap = n;
    while (gap > 1)
    {
        //gap = gap / 2;
        gap = gap / 3 + 1;
        for (int i = 0; i < n - gap; i++)
        {
            int end = i;
            int x = a[end + gap];
            while (end >= 0)
            {
                if (a[end] > x)
                {
                    a[end + gap] = a[end];
                    end -= gap;
                }
                else
                {
                    break;
                }
            }
            a[end + gap] = x;
        }
    }
}

阅读本段至此，我们可以发现一些问题？

1.gap越大，预排越快，预排后越不接近有序；

** **间距越大，意味着越小的数字能够很快的跳的前面来，越大的数字能很快的跳到后面去；虽然预排比较快，但是整体看不出来有序；
2.gap越小，预排越慢，预排后越接近有序；

** **** 间距越小，意味着它每部分的数据都接近于有序，整体相对有序，但是预排相对比较慢；**
3.gap == 1 ，就是直接插入排序；

** **当间距在发生变化时，不断进行预排，每次都在向有序靠近，知道最后间距变化为1时，就能将整个数组排列完成；

一般gap是如何确定呢？

** 起初，希尔大佬认为gap=n/2、gap=gap/2直到gap=1；后来Knuth提出取gap=gap/3+1.还有人认为取奇数为好，也有人提出取gap互质为好。无论哪一种主张都没有得到证明；小伙伴就可以以 gap=gap/2 或 gap=gap/3+1 来取；需要强调的是 gap=gap/3+1**

这里为什么需要加1呢？当有N个数据时且N为偶数时，除到最后是，gap就为0了，我们需要最后一次达到gap=1，去进行直接插入排序，所以这里加1的目的就在于此；

三、选择排序

思路1：

** 每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的 数据元素排完 。**

//选择排序1
void SelectSort(int* a, int n)
{
    int begin = 0;
    while (begin < n - 1)
    {
        int min = begin;
        for (int i = begin; i <= n - 1; i++)
        {
            if (a[i] < a[min])
            {
                min = i;//找最小值的下标
            }
        }
        Swap(&a[begin], &a[min]);
        ++begin;
    }
}

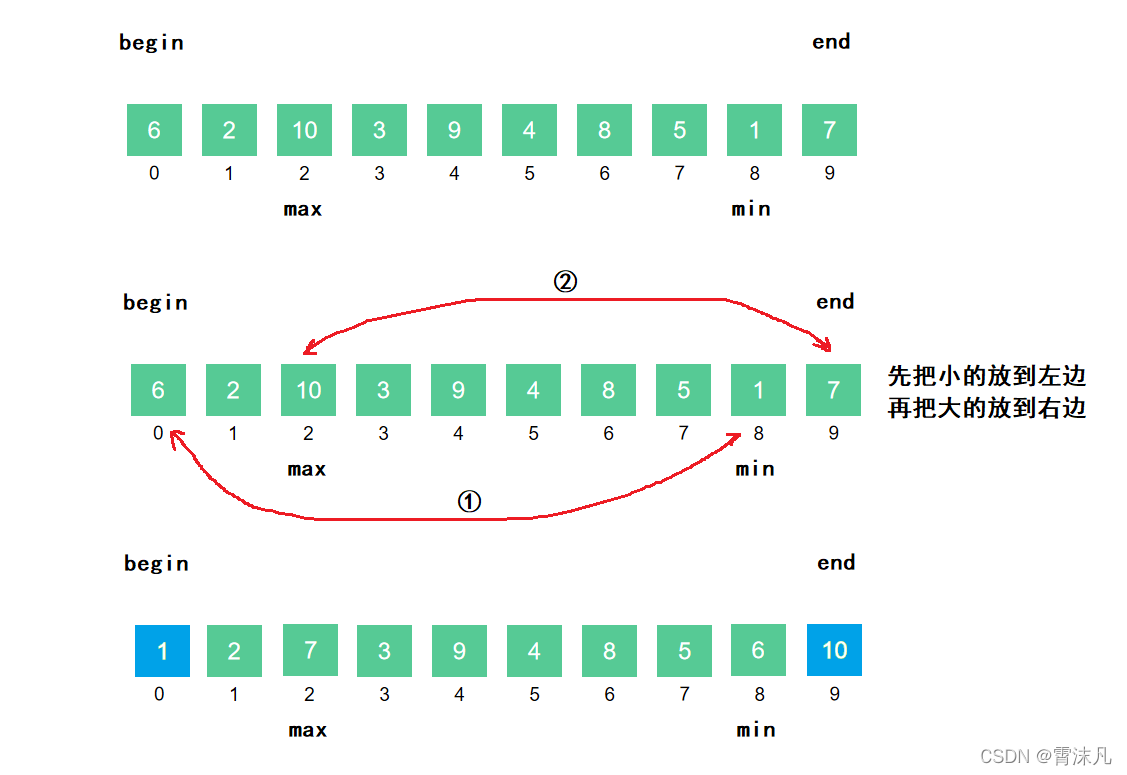
思路2：

** 思路1是每次选一个较小数（以升序为例）放到左边，直到全部排序完成；思路二的思想就是一次选两个数，小的放左边，大的放右边；**

** 注意点：**

如何解决呢？

此时最大值被换走了，我们可以修正一下max和min的位置；

// 选择排序2
void Swap(int* px, int* py)
{
    int tmp = *px;
    *px = *py;
    *py = tmp;
}
void SelectSort(int* a, int n)
{
    int begin = 0, end = n - 1;
    while (begin < end)
    {
        int mini = begin, maxi = begin;
        for (int i = begin; i <= end; i++)
        {
            if (a[i] < a[mini])
            {
                mini = i;//找最小值的下标
            }
            if (a[i] > a[maxi])
            {
                maxi = i;//找最大值的下标
            }
        }
        Swap(&a[begin], &a[mini]);
        //begin == maxi时，最大值被换走了，修正一下maxi的位置
        if (begin == maxi)
        {
            maxi = mini;
        }
        Swap(&a[end], &a[maxi]);
        ++begin;
        --end;
    }
}

四、堆排序

** 堆排序(Heapsort)是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆，排降序建小堆。**

向下调整算法：

堆排序：

如果对堆的应用还不清楚的小伙伴可以去看这里：

链接：https://blog.csdn.net/sjsjnsjnn/article/details/124201028?spm=1001.2014.3001.5501

//向下调整函数（大堆（升序）用大于，小堆（降序）用小于）
void AdjustDown(int* a, int n, int parent)
{
    assert(a);
    int child = parent * 2 + 1;
    while (child < n)
    {
        //选出左右孩子中小的那个
        if (child + 1 < n && a[child + 1] > a[child])
        {
            ++child;
        }

        //如果小的孩子小于父亲，则交换，并继续向下调整
        if (a[child] > a[parent])
        {
            Swap(&a[child], &a[parent]);
            parent = child;
            child = parent * 2 + 1;
        }
        else
        {
            break;
        }
    }
}

// 堆排序
void HeapSort(int* a, int n)
{
    //倒着建堆
    for (int i = (n - 1 - 1) / 2; i >= 0; --i)
    {
        AdjustDown(a, n, i);
    }
    //O(N*logN)
    int end = n - 1;
    while (end > 0)
    {
        Swap(&a[0], &a[end]);
        AdjustDown(a, end, 0);
        --end;
    }
}