机器学习（吴恩达）

定义：计算机程序从经验E中学习，解决某一任务T，进行某一性能度量P，通过P测定在T上的表现因经验E而提高，以跳棋游戏为例，经验E就是程序与自己下几万次跳棋，任务T就是玩跳棋，性能度量P就是与新对手玩跳棋时赢的概率。

目前有各种不同类型的学习算法，主流的是监督学习和无监督学习。监督学习就是个我们会教计算机做某件事情，无监督学习就是我们让计算机自己学习。

监督学习：我们给算法一个数据集，其中包含了正确答案，算法的目的就是给出更多的正确答案。用多组基础特征来预测我们需要的数据。实际上我们可能要处理无穷多的特征，因为你们计算机的内存可能要溢出，我们有一个灵巧的数学技巧来允许我们处理无穷多的基础特征，SVM，PCA等等。

无监督学习：我们仅仅被告知有一个数据集，无监督学习包含两个不同的簇，也就是分类，无监督学习可以把这些数据分成两个不同的簇，这就是聚类算法。当然，聚类仅仅是无监督学习的一种。你给算法大量的数据集，要求它找出数据的类型结构。

回归问题是预测一个连续值的输出，分类问题是预测离散值输出。

以线性回归为例，我们要得到的就是预测函数和实际值之间的误差平方和最小值也就是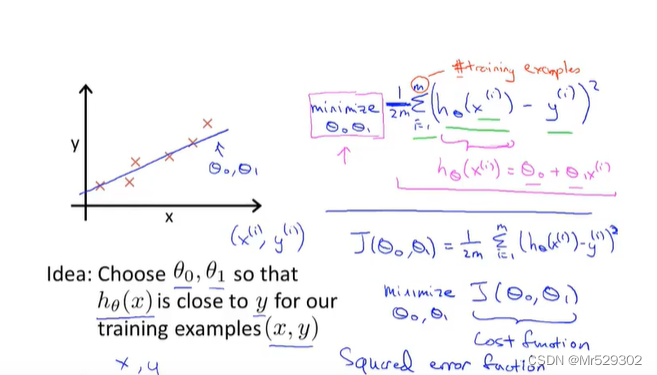

也称代价函数

而我们的目标就是要获得目标函数的最小值。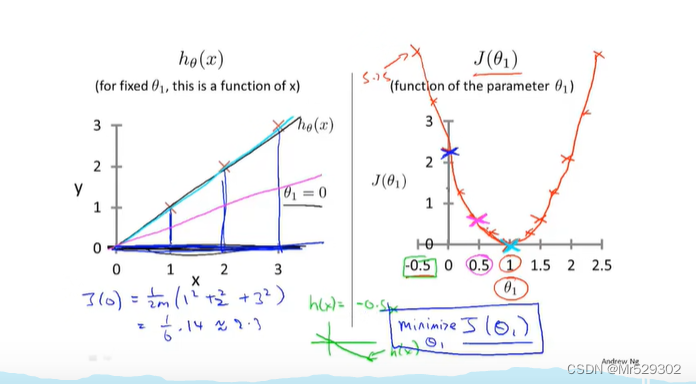

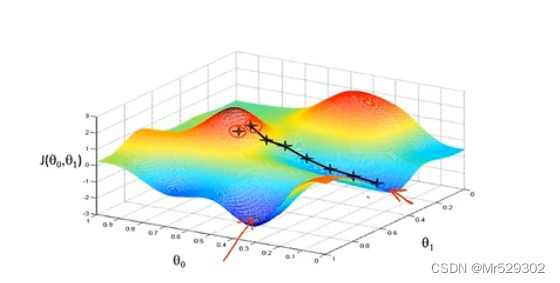
我们在上一章已经定义了可视化函数J，我们所要找的目标就是让可视化函数J达到最小值，那么我们要用什么样的方法呢

这里我们采用梯度下降法，这是一种常见的算法，他不仅仅可以用在线性回归上，还可以用在其他函数上。

1.赋予初始值（一般是0，0）

2.不停改变使J变小，搜寻下降速度最快的方向

3.直到我们找到最小值的局部收敛点，当然不一样的初始值他的局部收敛点也不一样。

这里的被成为一个学习率的数字，它用来控制梯度下降的时候我们迈出多大的步子，如果它的值很大，梯度下降就很迅速，如果很小，那么我们的速度就很慢。学习速率永远是一个正数。

在这个公式中，你需要同时更新两参数，

下面我们用一个更直观的例子来解释梯度下降法，以二维平面为例。

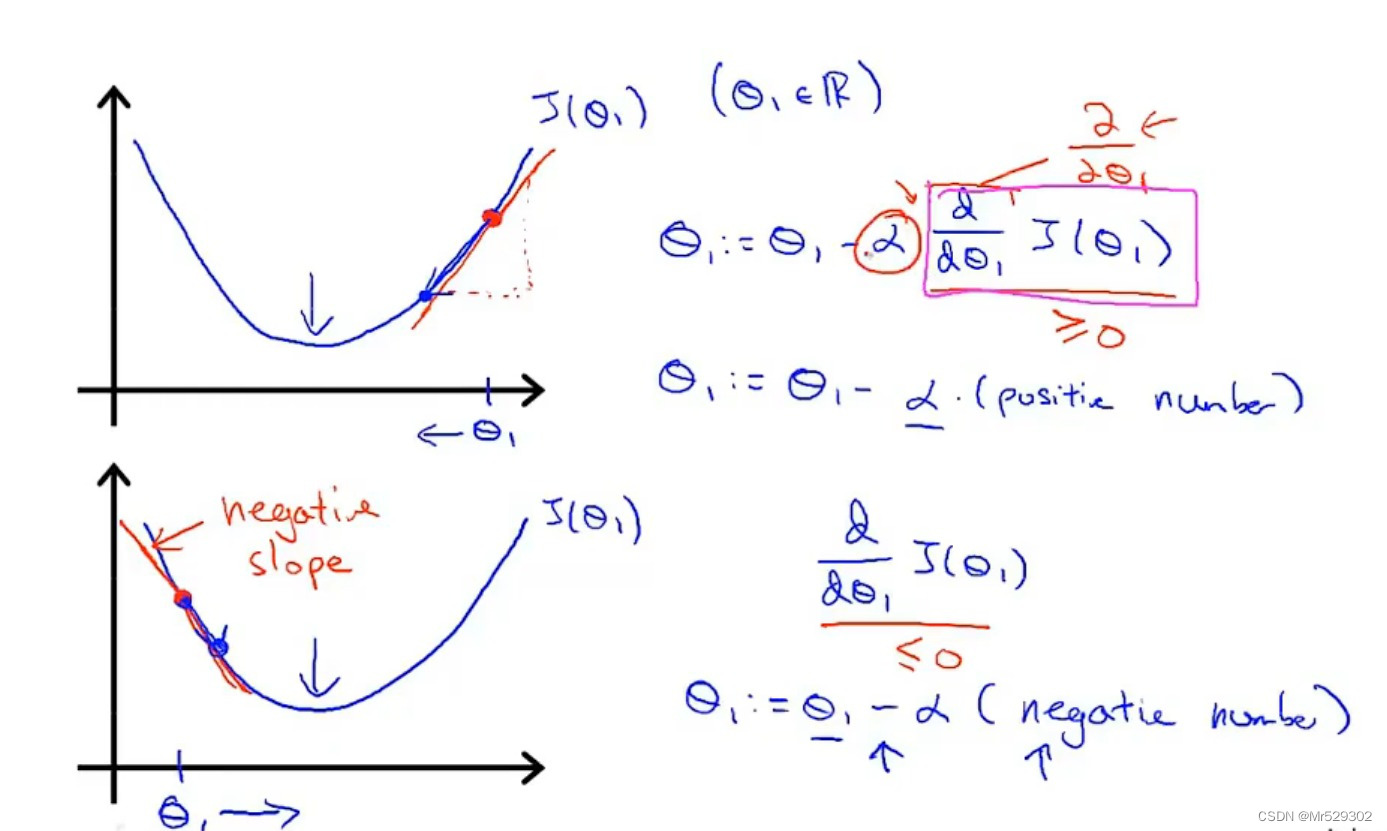
可以看到，不管是在左边还是右边，你都可以看到它会往最小值靠近。 而学习速率的选取很重要，如果太小了，那么说明它的步伐太慢，要很久才能达到最终目标，反过来，太大的话说明什么？说明它的步伐太大，可能会越过最终目标，进而离目标越来越远，导致无法收敛或发散。

这个梯度下降法有一个特点就是只能得到局部最优解，而无法得到全局最优解。

之前我们所用预测的函数值只有一个变量，也就是单特征，接下来我们要用到多特征来预测目标函数

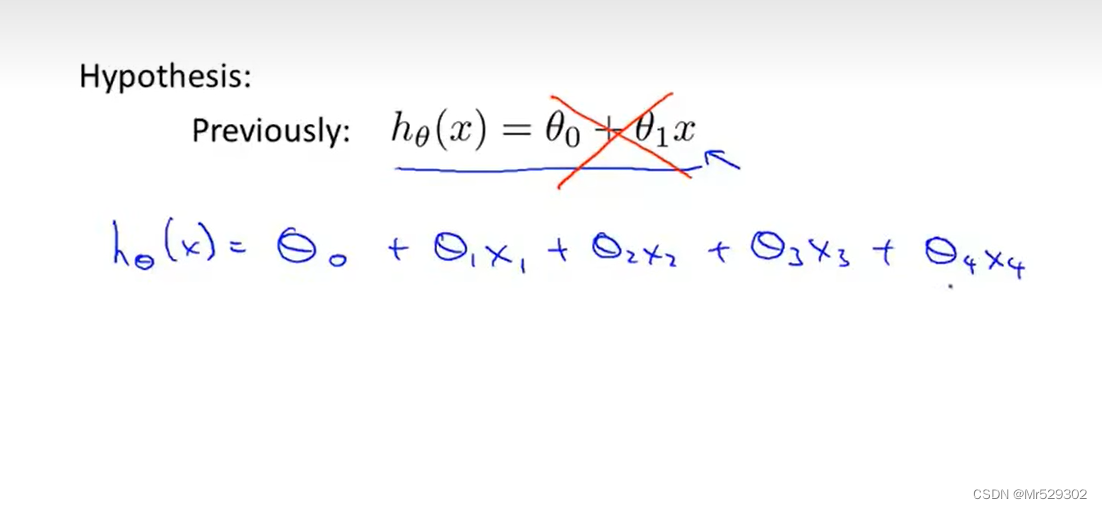
我们的线性回归问题就应该扩充到四个变量这里来

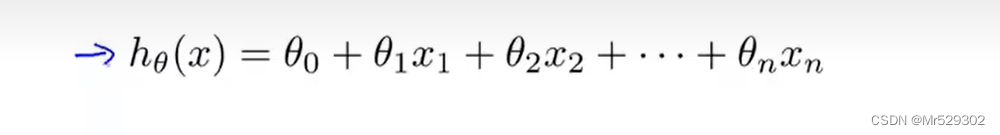
这就是所谓的多元线性回归，后面一般会跟一个X_0且设置为1为了匹配上向量，让两个可以互为向量做乘法

值得注意的是，如果你的特征取值很接近，以两个为例，那么它收敛的速度非常快，很快能取到局部最优解。反过来，如果他们取值相差过大，一个在1000到2000取值，一个在0到5取值，那么他们的收敛会非常慢

针对以上这种情况，我们就要对数据进行预处理，常用的手段有均值化，归一化等等，目的就是让不同特征的取值接近。

指的是这个特征的平均值，而值的是这个特征的范围，即最大值减去最小值。

通过使用这个方法，你可以让梯度下降的速度更快，迭代的次数更少，提高计算效率。不同的问题，他们的迭代次数也不是一样的。另外，并不是每一次迭代都会下降，有可能出现上升下降循环反复的情况。

**接下来，我们学习多项式回归。 **

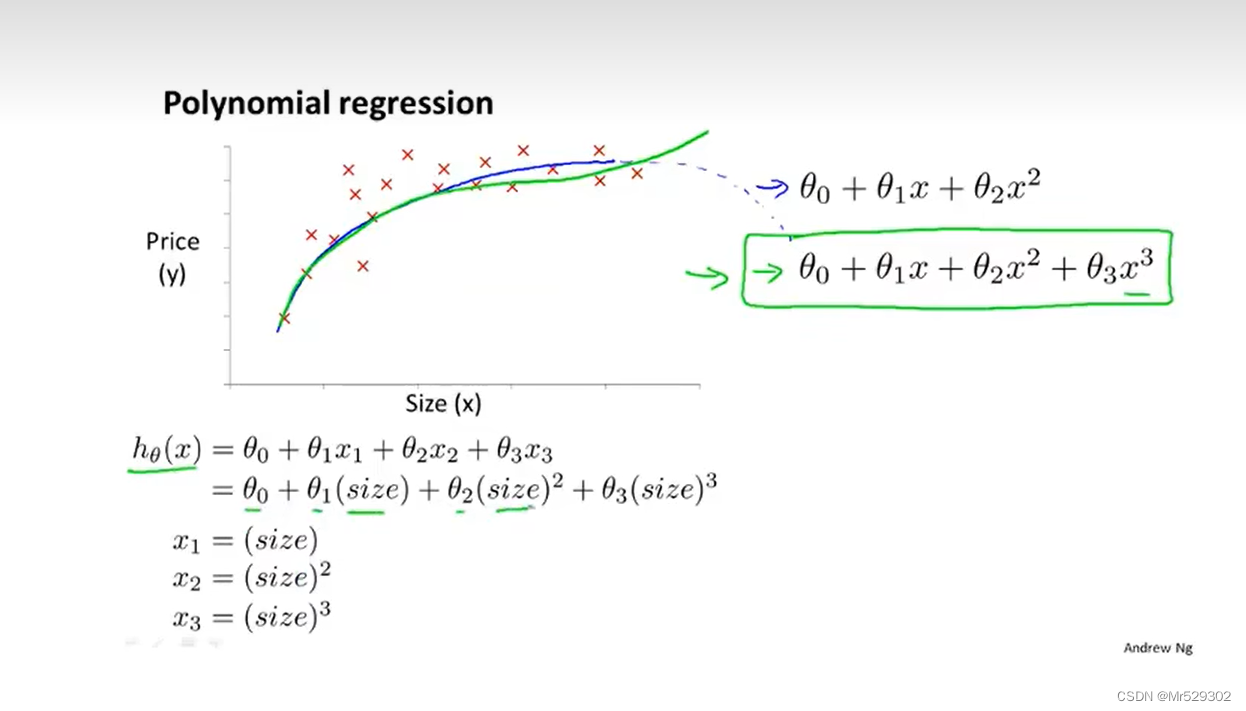
同样的，使用梯度下降法来迭代，接下来的正规方程只需要一次就可以得到结果。

以四个样本的普通训练集为例

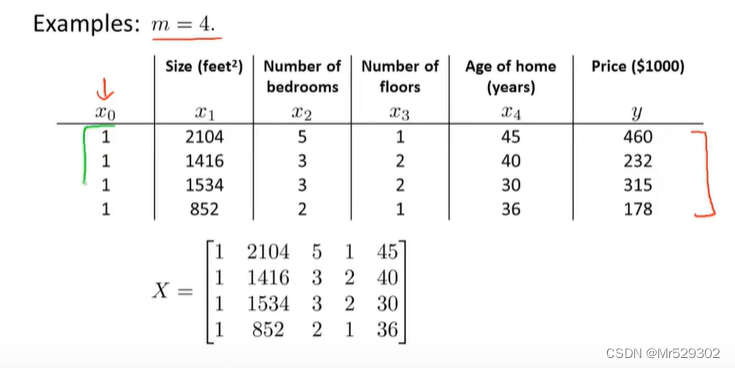
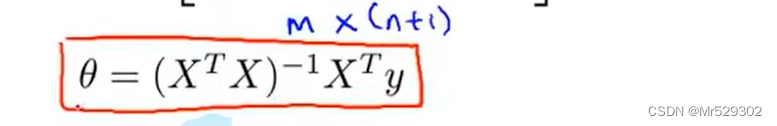
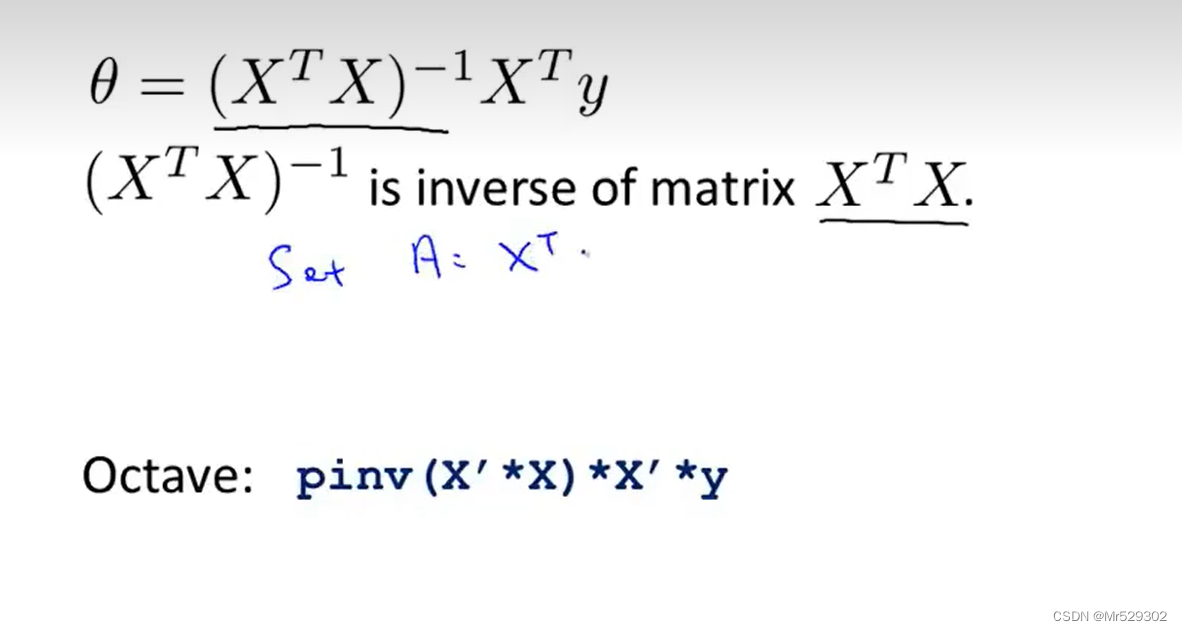
如果这样做，那么你就不需要进行特征缩放。

当然，我们知道，在计算逆矩阵的时候，通常以矩阵维度的三次方增长，当然，而逆矩阵那一项是n*n的维度，因此代价会相当之大。下面是两个方法的对比。

当不可逆时，也称奇异矩阵或退化矩阵。

包含了多余的特征，即有两个特征线性相关时候即不可逆。

** 我们一般不用线性回归来做分类问题**

我们接下来学习Logistic回归算法，他是一种分类算法，他的输出值介于0和1之间

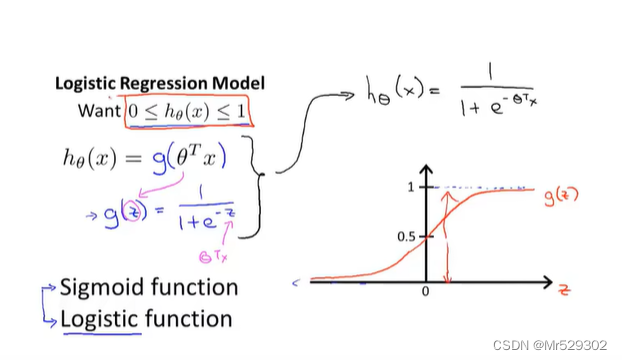
下面我们来学习决策边界，它可以帮助我们来理解假设函数在干什么？

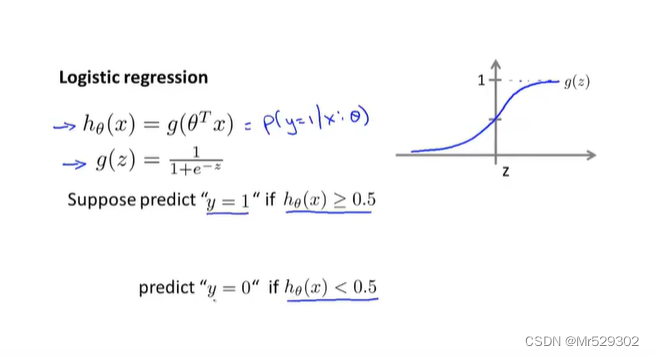
其中g为sigmod函数

其中这条线为决策边界。它将平面分成了两个部分 ，决策边界是假设函数的一个属性。

我们要用训练集数据来拟合，主要问题是如何避免代价函数使非凸函数 。所谓代价函数，就是用来衡量预测输出和真实值的偏差程度。

接下来我们就需要最小化代价函数，为什么要选择这样的代价函数，这是从统计函数中出来的，因为它的凸函数因此可以使用梯度下降找到局部收敛的点。

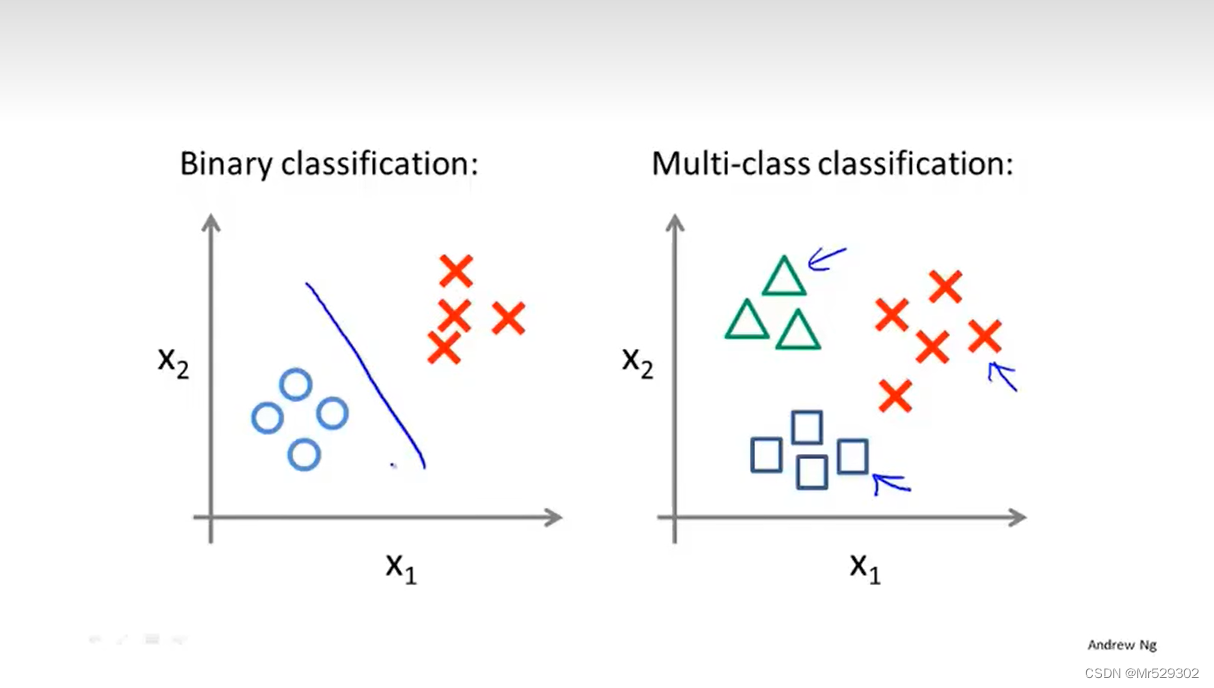
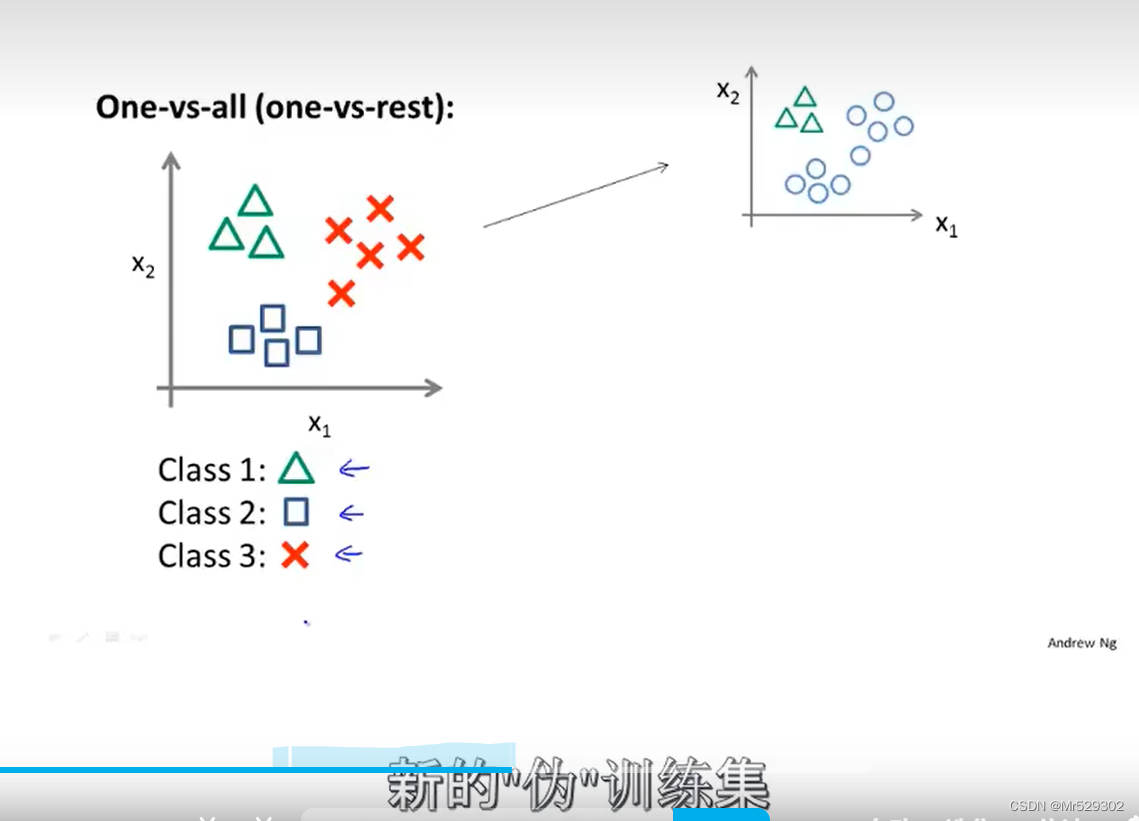
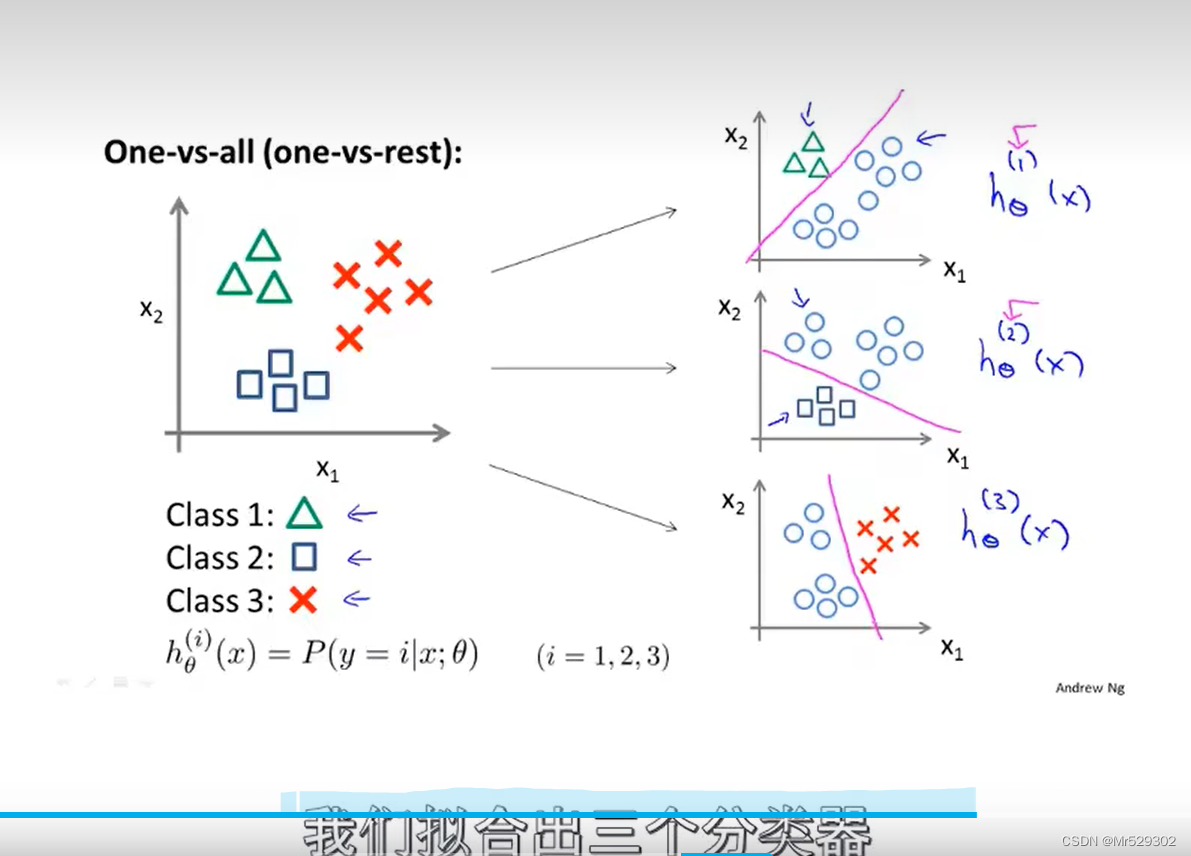
接下来我们学习如何使用Logistic回归来解决多分类问题。