Pytorch(二) —— 激活函数、损失函数及其梯度
1.激活函数
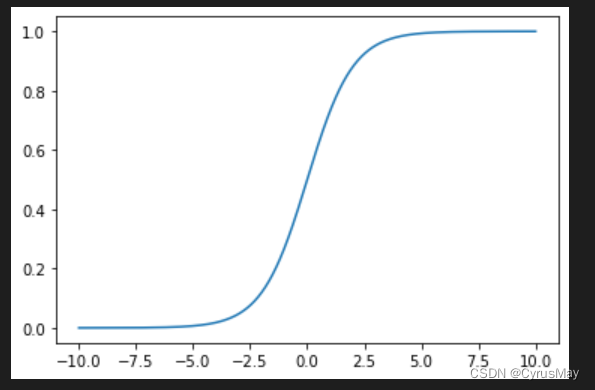
1.1 Sigmoid / Logistic
δ
(
x
)
=
1
1
+
e
−
x
δ
′
(
x
)
=
δ
(
1
−
δ
)
\delta(x)=\frac{1}{1+e^{-x}}\\\delta'(x)=\delta(1-\delta)
δ(x)=1+e−x1δ′(x)=δ(1−δ)
import matplotlib.pyplot as plt
import torch.nn.functional asF
x = torch.linspace(-10,10,1000)
y =F.sigmoid(x)
plt.plot(x,y)
plt.show()
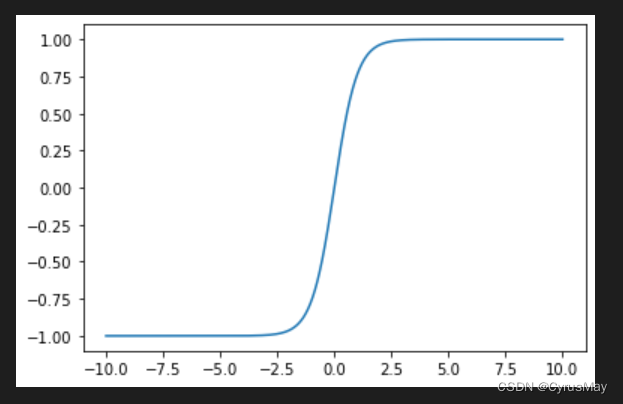
1.2 Tanh
t
a
n
h
(
x
)
=
e
x
−
e
−
x
e
x
+
e
−
x
∂
t
a
n
h
(
x
)
∂
x
=
1
−
t
a
n
h
2
(
x
)
tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}\\\frac{\partial tanh(x)}{\partial x}=1-tanh^2(x)
tanh(x)=ex+e−xex−e−x∂x∂tanh(x)=1−tanh2(x)
import matplotlib.pyplot as plt
import torch.nn.functional asF
x = torch.linspace(-10,10,1000)
y =F.tanh(x)
plt.plot(x,y)
plt.show()
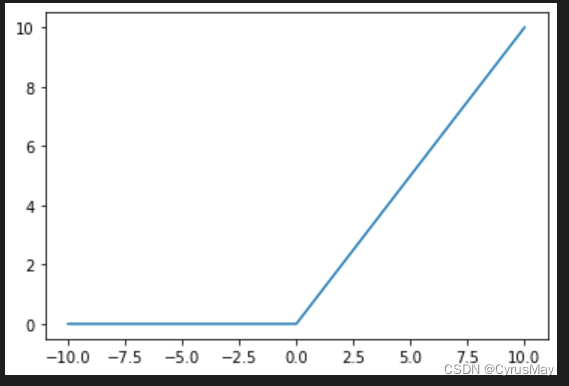
1.3 ReLU
f
(
x
)
=
m
a
x
(
0
,
x
)
f(x)=max(0,x)
f(x)=max(0,x)
import matplotlib.pyplot as plt
import torch.nn.functional asF
x = torch.linspace(-10,10,1000)
y =F.relu(x)
plt.plot(x,y)
plt.show()
1.4 Softmax
p
i
=
e
a
i
∑
k
=
1
N
e
a
k
∂
p
i
∂
a
j
=
{
p
i
(
1
−
p
j
)
i
=
j
−
p
i
p
j
i
≠
j
p_i=\frac{e^{a_i}}{\sum_{k=1}^N{e^{a_k}}}\\ \frac{\partial p_i}{\partial a_j}=\left\{ \begin{array}{lc} p_i(1-p_j) & i=j \\ -p_ip_j&i\neq j\\ \end{array} \right.
pi=∑k=1Neakeai∂aj∂pi={pi(1−pj)−pipji=ji=j
import torch.nn.functional asF
logits = torch.rand(10)
prob =F.softmax(logits,dim=0)print(prob)
tensor([0.1024, 0.0617, 0.1133, 0.1544, 0.1184, 0.0735, 0.0590, 0.1036, 0.0861,
0.1275])
2.损失函数
2.1 MSE
import torch.nn.functional asF
x = torch.rand(100,64)
w = torch.rand(64,1)
y = torch.rand(100,1)
mse =F.mse_loss(y,x@w)print(mse)
tensor(238.5115)
2.2 CorssEntorpy
import torch.nn.functional asF
x = torch.rand(100,64)
w = torch.rand(64,10)
y = torch.randint(0,9,[100])
entropy =F.cross_entropy(x@w,y)print(entropy)
tensor(3.6413)
3. 求导和反向传播
3.1 求导
- Tensor.requires_grad_()
- torch.autograd.grad()
import torch.nn.functional asFimport torch
x = torch.rand(100,64)
w = torch.rand(64,1)
y = torch.rand(100,1)
w.requires_grad_()
mse =F.mse_loss(x@w,y)
grads = torch.autograd.grad(mse,[w])print(grads[0].shape)
torch.Size([64, 1])
3.2 反向传播
- Tensor.backward()
import torch.nn.functional asFimport torch
x = torch.rand(100,64)
w = torch.rand(64,10)
w.requires_grad_()
y = torch.randint(0,9,[100,])
entropy =F.cross_entropy(x@w,y)
entropy.backward()
w.grad.shape
torch.Size([64, 10])
by CyrusMay 2022 06 28
人生 只是 须臾的刹那
人间 只是 天地的夹缝
——————五月天(因为你 所以我)——————
本文转载自: https://blog.csdn.net/Cyrus_May/article/details/125500584
版权归原作者 CyrusMay 所有, 如有侵权,请联系我们删除。
版权归原作者 CyrusMay 所有, 如有侵权,请联系我们删除。