黏菌算法（Slime Mould Algorithm，SMA）

文章目录

1 算法思想

黏菌算法由李世民等人发表于2020年，模拟了黏菌觅食过程中的行为和形态变化。

黏菌在有丝分裂后形成的变形体成熟之后，进入营养生长时期，会形成网状型态，且依照食物、水与氧气等所需养分改变其表面积。在黏菌算法中，黏菌会根据当前位置的客观条件（适应度函数优劣），决定每个个体所在位置的权重，然后个体会根据权重决定新的位置在哪。

当黏菌接近食物源时，生物振荡器会通过静脉产生传播波，来增加细胞质流量。食物浓度越高，生物振荡器产生的传播波越强，细胞质流动越快。黏菌算法就是通过模拟黏菌这种捕食行为来实现智能寻优功能的。

借鉴黏菌的生物行为，可以抽象出三个规则：

1. 接近食物： 黏菌通过空气中的气味接近食物，黏菌接近食物时呈圆形与扇形结构运动。
2. 包围食物： 黏菌静脉接触的食物浓度越高，生物振荡器产生的传播波越强，细胞质流动越快。
3. 抓取食物： 黏菌在食物浓度低时更慢地接近食物，找到优质食物时更快地接近食物。

2 算法步骤

1. 设置参数，初始化种群，计算适应度值；
2. 更新黏菌权重W、参数a、参数b： W = { 1 + r × l o g ( b F − S ( i ) b F − w F + 1 ) , i f 该 个 体 的 适 应 度 值 排 在 群 体 前 一 半 1 − r × l o g ( b F − S ( i ) b F − w F + 1 ) , e l s e 在 后 一 半 W=\left{ \begin{aligned} 1+r×log(\frac{bF-S(i)}{bF-wF}+1) , & if 该个体的适应度值排在群体前一半 \ 1-r×log(\frac{bF-S(i)}{bF-wF}+1) , & else 在后一半 \end{aligned} \right. W=⎩⎪⎪⎨⎪⎪⎧​1+r×log(bF−wFbF−S(i)​+1),1−r×log(bF−wFbF−S(i)​+1),​if该个体的适应度值排在群体前一半else在后一半​ （下面有参数说明表） 公式解读：前一半较优部分个体的权重取值较大，在[1,1.3]内；较差的后一半取值在[0.7,1]内，越差的个体权重越接近0.7。取log的作用就是减缓了W的变化率。 a = a r c t a n h ( b ) b = 1 − t T a=arctanh(b) \ b=1-\frac{t}{T} a=arctanh(b)b=1−Tt​ b的变化是一条线性递减的简单直线，a的变化如下图：
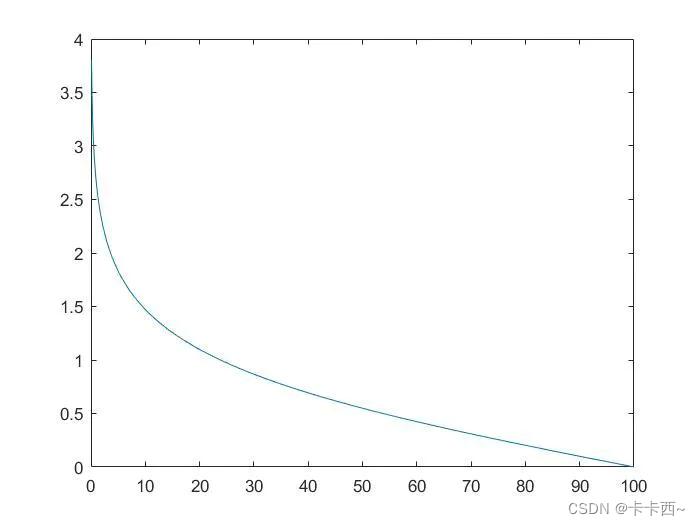
3. 更新个体位置 X ( t + 1 ) X(t+1) X(t+1)，分三种情况： X ( t + 1 ) = { r × ( u b − l b ) + l b , r < z X b ( t ) + v b ( W × X A ( t ) − X B ( t ) ) , z ≤ r < p v c × X ( t ) , p ≤ r X(t+1)=\left{ \begin{aligned} &r×(ub-lb)+lb, & r<z \ &X_b(t)+vb(W×X_A(t)-X_B(t)), & z \le r<p \ &vc×X(t), & p \le r \end{aligned} \right. X(t+1)=⎩⎪⎨⎪⎧​​r×(ub−lb)+lb,Xb​(t)+vb(W×XA​(t)−XB​(t)),vc×X(t),​r<zz≤r<pp≤r​ （下面有参数说明表） 若r<z，按第一个子公式更新位置；否则更新 p , v b , v c p,vb,vc p,vb,vc，并比较r和p，p的计算如下： p = t a n h ( ∣ S ( i ) − D F ∣ ) , i = 1 , 2 , . . . , N v b = [ − a , a ] ， v c = [ − b , b ] p=tanh(|S(i)-DF|),i=1,2,...,N \ vb = [-a,a]，vc= [-b,b] p=tanh(∣S(i)−DF∣),i=1,2,...,Nvb=[−a,a]，vc=[−b,b] p的变化如下图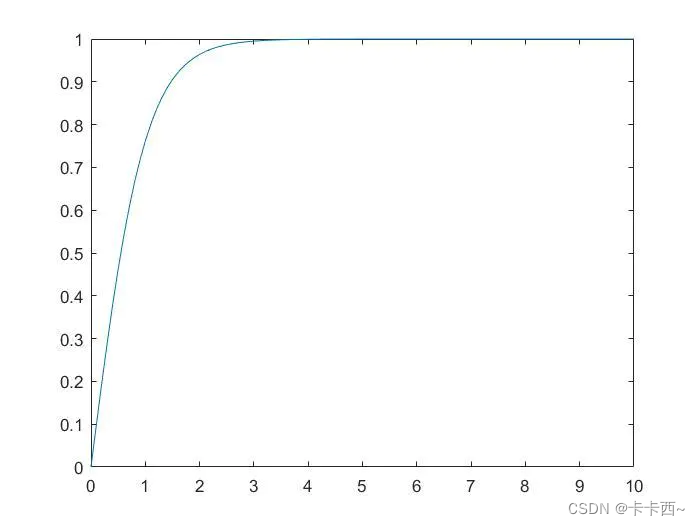： 若r<p，按第二个子公式更新位置；否则，按第三个子公式更新位置。

更新个体位置这一步模拟了黏菌的生物行为：利用生物振荡器产生的传播波改变静脉中的细胞质流动速度。
算法是这样模拟的：通过vb，vc，W来模拟静脉宽度的变化和振荡器振荡频率变化，当食物浓度低时，慢慢接近食物，扩大全局搜索能力，当找到优质食物时，迅速接近食物，加强局部搜索能力。
公式解读：第一个子公式获取的是全局随机位置，类似于GA中的变异操作；第二个是在当前最优位置的附近搜索，类似于局部搜索；第三个没看懂，好像会让个体最优值能收敛到0，当最优解不为0时效果不好。

1. 计算适应度值，更新全局最优解；
2. 判断是否满足结束条件，若不满足，返回步骤2。

参数说明表：
符号含义符号含义W黏菌重量a，p一个参数r随机数[0,1]S(i)第i个黏菌个体的适应度值bF当前迭代中最优适应度值wF当前迭代中最差适应度值t当前迭代次数T最大迭代次数vb随机数[-a,a]vc随机数[-b,b]DF所有迭代中的最优适应度值N黏菌的种群规模ub搜索空间的上界lb搜索空间的下界

       X
      
      
       (
      
      
       t
      
      
       )
      
     
     
      X(t)
     
    
   X(t)第t次迭代时黏菌的位置
   
    
     
      
       
        X
       
       
        b
       
      
      
       (
      
      
       t
      
      
       )
      
     
     
      X_b(t)
     
    
   Xb​(t)第t次迭代时的最佳位置
   
    
     
      
       
        X
       
       
        A
       
      
      
       (
      
      
       t
      
      
       )
      
      
       ,
      
      
       
        X
       
       
        B
       
      
      
       (
      
      
       t
      
      
       )
      
     
     
      X_A(t),X_B(t)
     
    
   XA​(t),XB​(t)第t次迭代时随机选择的两个黏菌个体z随机分布的黏菌个体占总体的比例

3 求函数最值（Python实现）

求解下列函数的最小值：

     f
    
    
     (
    
    
     
      x
     
     
      1
     
    
    
     ,
    
    
     
      x
     
     
      2
     
    
    
     )
    
    
     =
    
    
     
      x
     
     
      1
     
     
      2
     
    
    
     +
    
    
     
      x
     
     
      2
     
     
      2
     
    
   
   
     f(x_1,x_2)=x_1^2+x_2^2 
   
  
 f(x1​,x2​)=x12​+x22​

标准答案是0，函数长这个样子：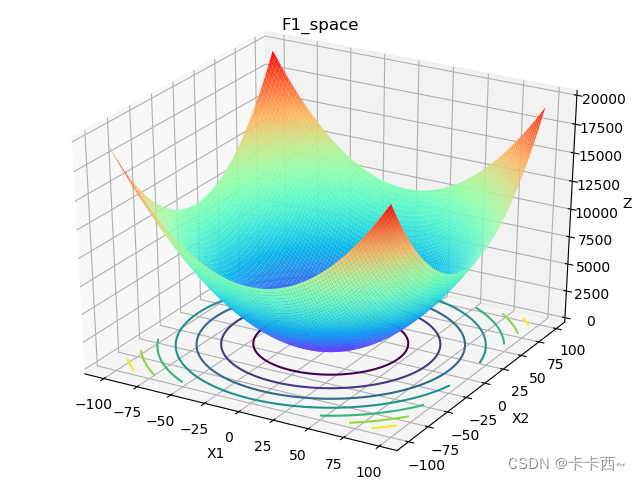

主函数：

import numpy as np
from matplotlib import pyplot as plt
import SMA

'''适应度函数'''deffun(X):
    Results = np.sum(X **2)return Results

'''主函数 '''# 设置参数
pop =30# 种群数量
MaxIter =500# 最大迭代次数
dim =2# 维度
lb =-10* np.ones(dim)# 下边界
ub =10* np.ones(dim)# 上边界# 调用SMA算法
GbestScore, GbestPositon, Curve = SMA.SMA(pop, dim, lb, ub, MaxIter, fun)print('最优适应度值：', GbestScore)print('最优解[x1,x2]：', GbestPositon)# 绘制适应度曲线
plt.figure(1)
plt.plot(Curve,'r-', linewidth=2)
plt.xlabel('Iteration', fontsize='medium')
plt.ylabel("Fitness", fontsize='medium')
plt.grid()
plt.title('SMA', fontsize='large')
plt.show()

SMA.py：

import numpy as np
import copy as copy

'''黏菌优化算法''''''

Args:
    pop: 种群数量
    dim: 个体维度
    lb: 下边界，维度[1,dim]
    ub: 上边界，维度[1,dim]
    MaxIter: 最大迭代次数
    fun: 适应度函数接口

Returns:
    GbestScore: 最优解对应的适应度值
    GbestPositon: 最优解
    Curve: 画迭代曲线用的
    
'''defSMA(pop, dim, lb, ub, MaxIter, fun):# 1.设置参数，初始化种群，并计算适应度值# 设置参数
    z =0.03# 一个参数，更新个体位置时用，表示随机分布的黏菌个体占总体的比例
    Curve = np.zeros([MaxIter,1])# 画迭代图用
    W = np.zeros([pop, dim])# 黏菌权重# 初始化种群
    X = initialization(pop, ub, lb, dim)# 计算适应度值
    fitness = CaculateFitness(X, fun)# 计算适应度值
    fitness, sortIndex = SortFitness(fitness)# 对适应度值排序
    X = SortPosition(X, sortIndex)# 种群排序
    GbestScore = copy.copy(fitness[0])
    GbestPositon = copy.copy(X[0,:])for t inrange(MaxIter):
        worstFitness = fitness[-1]
        bestFitness = fitness[0]
        S = bestFitness - worstFitness +10E-8# 当前最优与最差适应度的差值，算权重W用，10E-8为极小值，避免分母为0；# 2.更新权重W和参数a、参数b# 权重Wfor i inrange(pop):if i < pop /2:# 适应度值排前一半的W计算
                W[i,:]=1+ np.random.random([1, dim])* np.log10((bestFitness - fitness[i])/(S)+1+10E-8)else:# 适应度值排后一半的W计算
                W[i,:]=1- np.random.random([1, dim])* np.log10((bestFitness - fitness[i])/(S)+1+10E-8)# 参数b
        b =1-(t / MaxIter)# 参数aif b !=-1and b !=1:
            a = np.math.atanh(b)else:
            a =1# 3.位置更新，分三种情况for i inrange(pop):# 3.1如果r<z，按第一个子公式更新位置if np.random.random()< z:
                X[i,:]=(ub.T - lb.T)* np.random.random([1, dim])+ lb.T
            # 否则，更新参数p，vb，vc，继续判断else:
                p = np.tanh(abs(fitness[i]- GbestScore))
                vb =2* a * np.random.random([1, dim])- a
                vc =2* b * np.random.random([1, dim])- b
                for j inrange(dim):
                    r = np.random.random()
                    A = np.random.randint(pop)# 随机选择两个黏菌个体
                    B = np.random.randint(pop)# 3.2如果r<p，按第二个子公式更新位置if r < p:
                        X[i, j]= GbestPositon[j]+ vb[0, j]*(W[i, j]* X[A, j]- X[B, j])# 3.3按第三个子公式更新位置else:
                        X[i, j]= vc[0, j]* X[i, j]

        X = BorderCheck(X, ub, lb, pop, dim)# 边界检查
        fitness = CaculateFitness(X, fun)# 计算适应度值
        fitness, sortIndex = SortFitness(fitness)# 对适应度值排序，得到排好序的适应度值和对应的索引
        X = SortPosition(X, sortIndex)# 根据排好序的索引对种群排序if(fitness[0]<= GbestScore):# 更新全局最优
            GbestScore = copy.copy(fitness[0])
            GbestPositon = copy.copy(X[0,:])
        Curve[t]= GbestScore

    return GbestScore, GbestPositon, Curve

运行结果：
最优适应度值： [6.28823104e-226]
最优解： [[-1.77578646e-113 1.77054045e-113]]
可以看到答案非常接近最优适应度值0。

4 算法进阶

集思广益：

1. W、vc、vb等参数的设置可以使个体在任意角度形成搜索向量，即在任意方向上搜索解空间，使算法具有找到最优解的可能性。
2. 文中对于帮助算法及时跳出局部最优值并没有做出很多的工作。
3. CEC2017效果一般。
4. CEC2014前几个函数效果很好，比别的算法可以优于几十个数量级，观察了一下这几个函数的最优值都是0，猜测可能和那个位置更新公式刻意逼近0有关。
5. CEC2014剩余函数效果一般，说明探索能力和跳出局部最优能力有待改善。
6. 黏菌算法没有贪心步骤，无论新位置好不好，个体都移动到新位置。

直接改进SMA

文献改进策略Shimin Li, Huiling Chen, Mingjing Wang, Ali Asghar Heidari,Seyedali Mirjalili.Slime mould algorithm: A new method for stochastic optimization,Future Generation Computer Systems,2020(111),300-323原论文网站改进了p的更新公式，位置更新公式的第三个子公式郭雨鑫,刘升,张磊,黄倩.精英反向与二次插值改进的黏菌算法[J].计算机应用研究,2021,38(12):3651-3656.精英反向学习，二次插值刘宇凇,刘升.无迹西格玛点引导的拟反向黏菌算法及其工程应用[J/OL].计算机应用研究:1-9[2022-10-17].布朗运动，莱维飞行机制Improved slime mould algorithm with elitist strategy and its application to structural optimization with natural frequency constraints,IEEE精英替换策略Dispersed foraging slime mould algorithm: Continuous and binary variants for global optimization and wrapper-based feature selection分散觅食策略Multilevel threshold image segmentation with diffusion association slime mould algorithm and Renyi’s entropy for chronic obstructive pulmonary disease扩散机制DM，关联策略AS张启明. 面向云计算任务调度的混合智能算法的研究[D].桂林理工大学,2022.Logistic混沌映射，差分进化A novel version of slime mould algorithm for global optimization and real world engineering problems: Enhanced slime mould algorithm.sigmoid代替arctanh

融合别的智能优化算法来改进SMA

文献融合的智能优化算法任丽莉,王志军,闫冬梅.结合黏菌觅食行为的改进多元宇宙算法[J].吉林大学学报(工学版),2021,51(06):2190-2197.多元宇宙算法MVO贾鹤鸣,刘宇翔,刘庆鑫,王爽,郑荣.融合随机反向学习的黏菌与算术混合优化算法[J].计算机科学与探索,2022,16(05):1182-1192.算术优化算法AOA刘成汉,何庆.改进交叉算子的自适应人工蜂群黏菌算法[J/OL].小型微型计算机系统:1-8[2022-10-17]. // An efficient multilevel thresholding image segmentation method based on the slime mould algorithm with bee foraging mechanism: A real case with lupus nephritis images人工蜂群ABC郑旸,龙英文,吉明明,顾嘉城.融合螺旋黏菌算法的混沌麻雀搜索算法与应用[J/OL].计算机工程与应用:1-11[2022-10-17].麻雀搜索SSA翟青海,谢晓兰.混合云环境下考虑工作流的任务调度策略[J].桂林理工大学学报,2021,41(04):891-896.粒子群PSO刘磊. 基于群智能优化的多阈值图像分割方法研究及应用[D].长春师范大学,2022. // 张启明. 面向云计算任务调度的混合智能算法的研究[D].桂林理工大学,2022. // Performance optimization of differential evolution with slime mould algorithm for multilevel breast cancer image segmentation差分进化A novel version of slime mould algorithm for global optimization and real world engineering problems: Enhanced slime mould algorithm.正余弦算法SCAGradient-based optimizer improved by Slime Mould Algorithm for global optimization and feature selection for diverse computation problems基于梯度的优化算法An entropy minimization based multilevel colour thresholding technique for analysis of breast thermograms using equilibrium slime mould algorithm平衡算法EOHSMA_WOA: A hybrid novel Slime mould algorithm with whale optimization algorithm for tackling the image segmentation problem of chest X-ray images鲸鱼优化算法LSMA-TLBO: A hybrid SMA-TLBO algorithm with lévy flight based mutation for numerical optimization and engineering design problems教与学TLBOTowards augmented kernel extreme learning models for bankruptcy prediction: Algorithmic behavior and comprehensive analysis果蝇算法FOA

SMA及其改进的应用

文献应用高铖铖,陈锡程,张瑞,宋秋月,易东,伍亚舟.三种新型智能算法在疫情预警模型中的应用——基于百度搜索指数的COVID-19疫情预警[J].计算机工程与应用,2021,57(08):256-263.最小二乘支持向量机LSSVM，百度搜索指数疫情预警模型田中大,潘信澎.小波消噪和优化支持向量机的网络流量预测[J/OL].北京邮电大学学报:1-7[2022-10-17].DOI:10.13190/j.jbupt.2021-146. // 唐雄. 基于改进黏菌优化算法的入侵检测研究[D].广西民族大学,2021.支持向量机，网络流量预测模型，入侵检测臧传涛,刘冉冉,颜海彬.基于SMA-LSTM的轴承剩余寿命预测方法[J].江苏理工学院学报,2022,28(02):110-120.LSTM，轴承剩余使用寿命预测王鑫禄,刘大有,刘思含,王征,张丽伟,董飒.基于黏菌算法的蛋白质多序列比对[J/OL].吉林大学学报(工学版):1-11[2022-10-17].预测蛋白质结构A fast community detection algorithm based on coot bird metaheuristic optimizer in social networks社区检测CDOptimization of MLP neural network for modeling flow boiling performance of Al2O3/water nanofluids in a horizontal tube多层感知机MLP，人工神经网络ANN，反向传播算法BPGradient-based optimizer improved by Slime Mould Algorithm for global optimization and feature selection for diverse computation problems特征选择Towards augmented kernel extreme learning models for bankruptcy prediction: Algorithmic behavior and comprehensive analysisKELM分类器，破产预测韦鸳叶. 启发式黏菌优化算法及应用研究[D].广西民族大学,2022.无线传感器覆盖优化，无功功率优化调度，无人机动态目标搜索Implementing modified swarm intelligence algorithm based on Slime moulds for path planning and obstacle avoidance problem in mobile robots自主移动机器人AMR，路径规划与避障问题A Decomposition based Multi-Objective Heat Transfer Search algorithm for structure optimization多目标问题翟青海,谢晓兰.混合云环境下考虑工作流的任务调度策略[J].桂林理工大学学报,2021,41(04):891-896. // 张启明. 面向云计算任务调度的混合智能算法的研究[D].桂林理工大学,2022.云计算工作流调度，任务调度

参考书籍：范旭，《Python智能优化算法——从原理到代码实现与应用》第一版，电子工业出版社。