⭐️前面的话⭐️
本篇文章带大家认识Java集合——Stack,Stack就是栈的意思,是一种数据结构,又叫先进后出表,本文首先会介绍数据结构《栈》,了解清楚栈的特点与性质,然后会根据栈的性质简单来模拟栈以及集合框架Stack类常见方法的使用。
Tips:数据结构——链表,在博主的历史文章中介绍过并通过Java和C语言都实现模拟过,所以对链表不再多赘述,集合框架中LinkedList类底层就是使用双链表实现的,因此在Java中可以使用LinkedList对象来使用链表,如果对链表不了解,可以去博主数据结构与算法专栏了解。
📒博客主页:未见花闻的博客主页
🎉欢迎关注🔎点赞👍收藏⭐️留言📝
📌本文由未见花闻原创,CSDN首发!
📆首发时间:🌴2022年1月20日🌴
✉️坚持和努力一定能换来诗与远方!
💭参考书籍:📚《Java核心技术》,📚《Java编程思想》,📚《Effective Java》
💬参考在线编程网站:🌐牛客网🌐力扣
博主的码云gitee,平常博主写的程序代码都在里面。
博主的github,平常博主写的程序代码都在里面。
🙏作者水平很有限,如果发现错误,一定要及时告知作者哦!感谢感谢!
📌导航小助手📌

题外话:在正式开始之前,我们先来看一看集合框架,画上√的表示博主已经介绍完毕了,可以翻看JavaSE系列专栏进行寻找,画上⭐️表示本文所介绍的内容。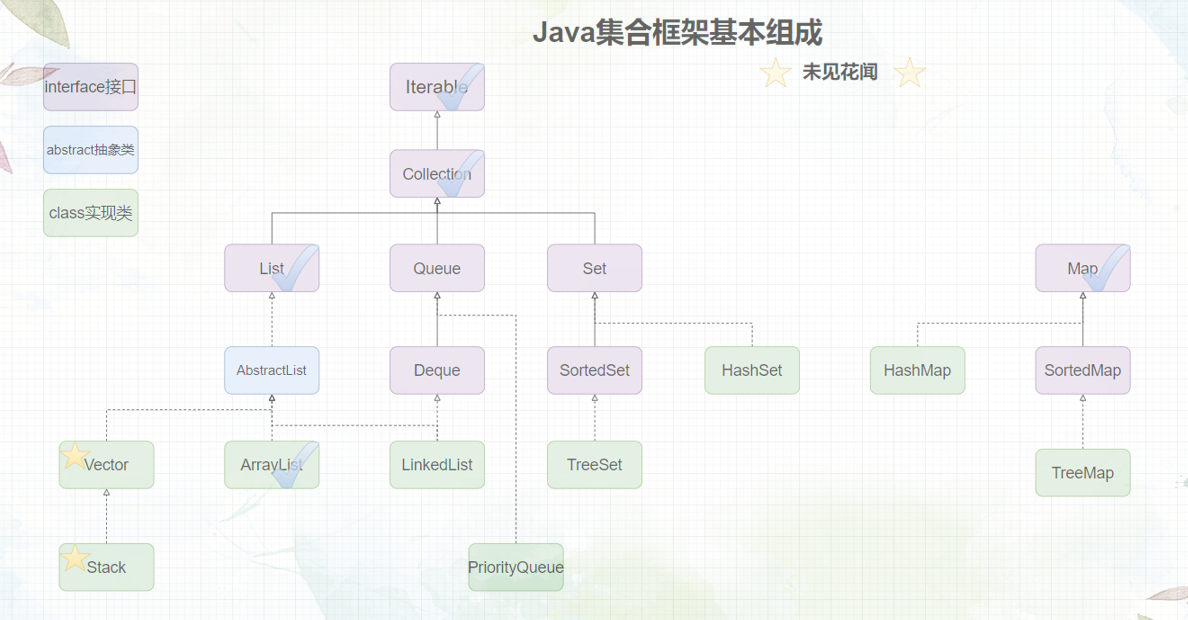
1.栈
1.1栈的特点
栈是一种组织数据的方式,栈内的元素有先进后出的特点,因此也叫做先进后出表,由此我们能够得到栈的概念:栈是一种只能在一端进行插入或删除操作的线性表。栈常常由顺序表或双链表实现,Java的Stack类底层就是由顺序表实现的,当然LinledList底层是一个双链表,由此LinkedList也可以当做栈来使用。
如果你现在对于栈还不能理解,你可以想象栈就是一个“死胡同”,只能一端进或者出。
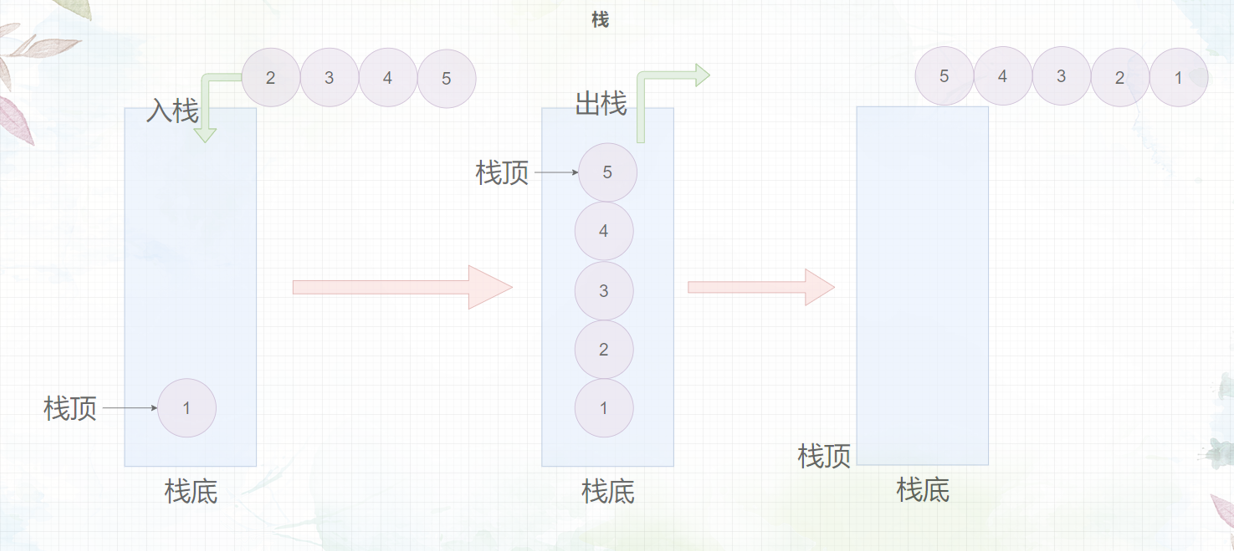
栈的几个术语:
允许进行插入、删除操作的一端称为栈顶;栈的另一端称为栈底。
当栈中没有数据元素时,称为空栈。
栈的插入操作通常称为进栈或入栈(压栈)。
栈的删除操作通常称为退栈或出栈。
1.2栈的常见应用
1.2.1验证栈的压入、弹出序列
给你入栈序列,判断不可能的出栈序列,见例题:
选项A: a,b,c依次入栈,c出栈,d入栈,d出栈,b,a依次出栈,出栈序列为c,d,b,a,所以选项A的出栈序列是可能的。
选项B: a,b,c,d依次入栈,d,c,b,a依次出栈,出栈序列为d,c,b,a,所以选项B的出栈序列是可能的。
选项C: a入栈,a出栈,b,c依次入栈,c出栈,d入栈,d出栈,b出栈,出栈序列为a,c,d,b所以选项C的出栈序列是可能的。
选项D: a,b,c,d依次入栈,d出栈,后一个出栈元素不可能是a,所以选项D的出栈序列是不可能的。
举一反三,看下面一道题:
p
3
p_3
p3的取值除了不能取到3其他的值均有可能,因此
p
3
p_3
p3取值个数为
n
−
1
n-1
n−1。
1.2.2前,中,后缀表达式
我们常用的数学加减乘除运算表达式都是中缀表达式,比如
1
+
1
+
6
∗
8
1+1+6*8
1+1+6∗8,将中缀表达式按运算顺序打上不同的的括号对,分别将运算符移到对应括号最右边,再将所有括号擦除,就能得到**后缀表达式**,同理将运算符移到到对应括号最左边就是**前缀表达式**。

2.Stack
2.1Stack类的使用
2.1.1Stack类与Vector类
Stack类的继承实现关系图如下,不妨把它称作Stack的家谱吧: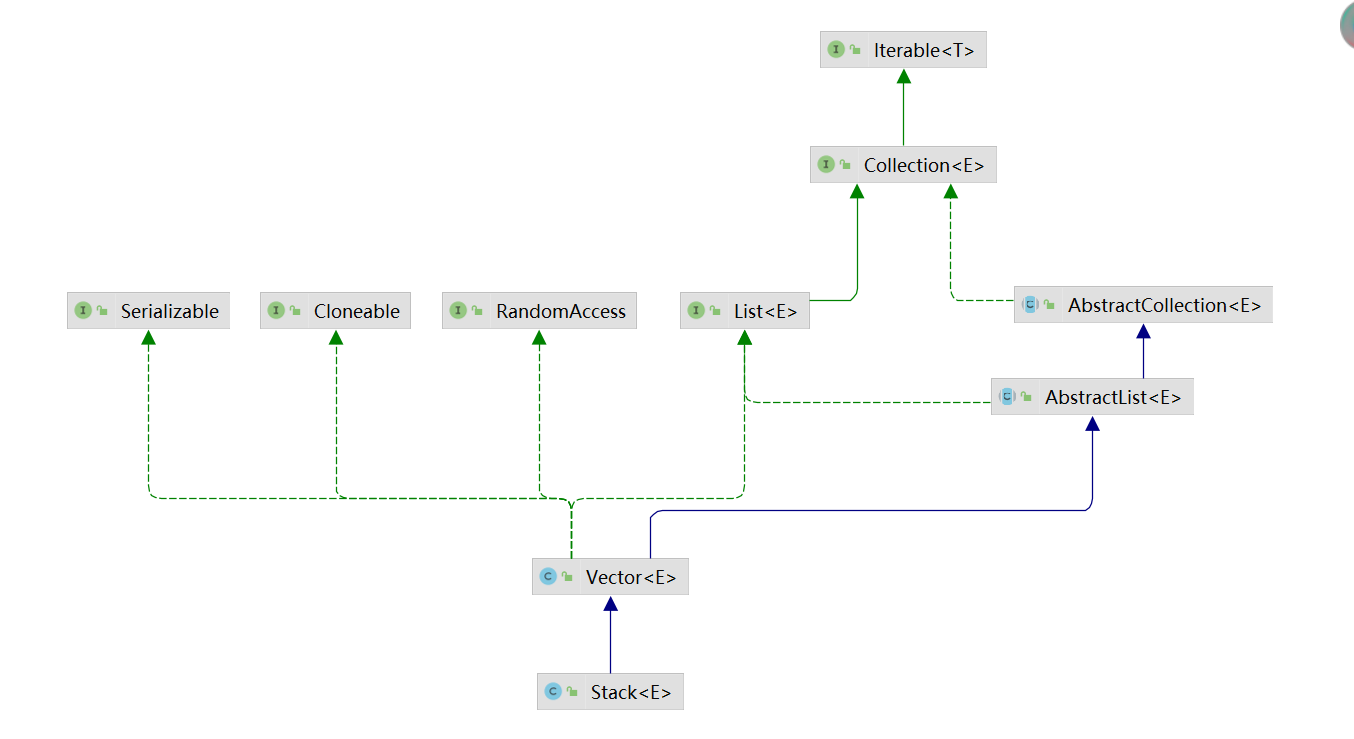
我们发现Stack支持序列化,克隆,随机访问,for-each循环遍历,Collection,List接口,Vector都可以引用Stack对象.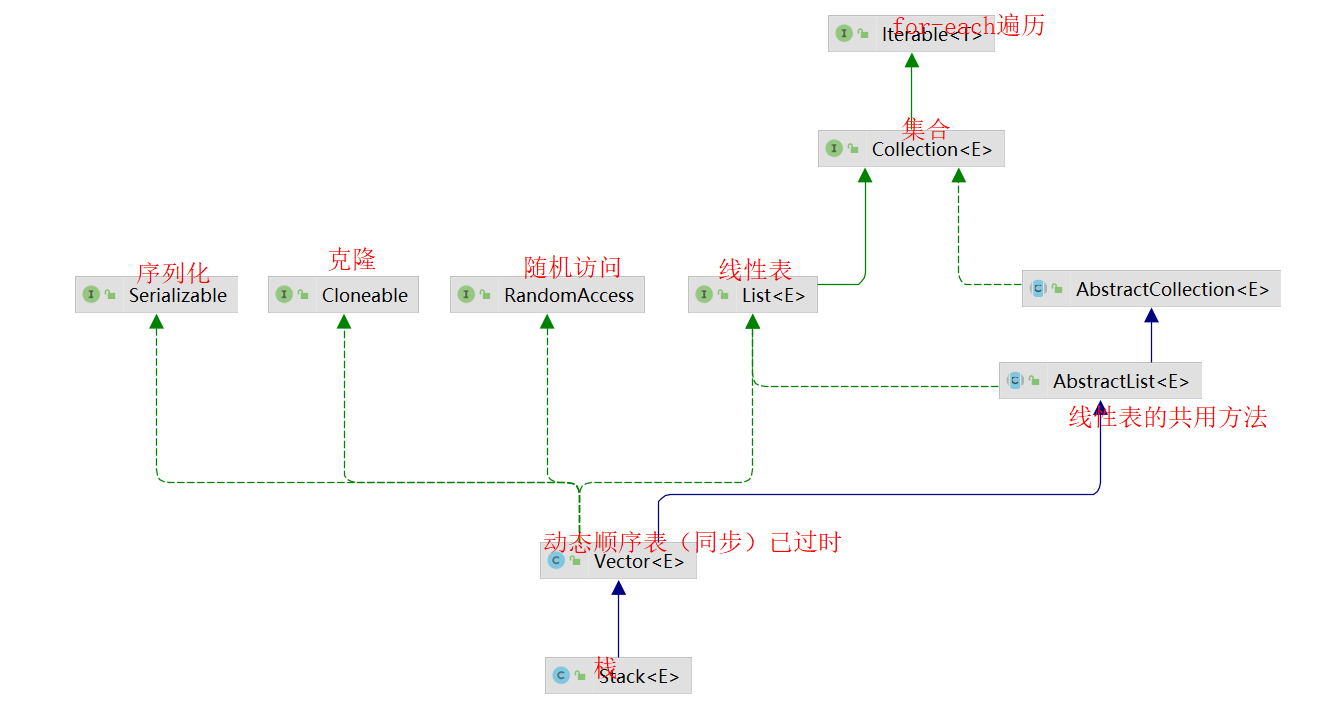
Vector与ArrayList基本是一致的,不同的是Vector是线程安全的,会在可能出现线程安全的方法前面加上
synchronized
关键字。
对于Vector类,是线程安全的动态数组,但是性能较差,可以说Vector已经过时了,不常用了,取而代之的是性能更强的CopyOnWriteArrayList。所以本文着重介绍Stack类,Vector类不多阐述。
因为Vector是线程安全的,那它的子类Stack自然也是线程安全的。
Vector & ArrayList & CopyOnWriteArrayList 三者的区别:
这三个集合类都继承List接口,都是动态的顺序表,其不同点如下:
- ArrayList是线程不安全的;
- Vector是比较古老的线程安全的,但性能不行;
- CopyOnWriteArrayList在兼顾了线程安全的同时,又提高了并发性,性能比Vector有不少提高。
2.1.2常用方法
方法类型作用public Stack()构造方法新建一个Stack对象public E push(E item)普通方法入栈public synchronized E pop()普通方法出栈public synchronized E peek()普通方法获取栈顶元素public boolean empty()普通方法判断栈是否为空栈public synchronized E peek()普通方法基于栈顶位置(索引为1,索引自栈顶向栈底递增)查找对象o,如果找到返回索引值,否则返回-1
这些方法的使用结合后文的题目进行演示。
2.2Stack简单模拟实现
栈的基本结构:数组(泛型)+ 栈顶指针
publicclassMyStack<E>{privateE[] elem;//栈空间privateint top;//栈顶索引}
入栈push+出栈pop+判断栈是否为空empty+获取栈顶元素peek+toString方法:
publicclassMyStack<E>{privateE[] elem;privateint top;publicMyStack(){this.elem =(E[])newObject[10];this.top =0;}publicvoidpush(E e){if(top ==this.elem.length){this.elem =Arrays.copyOf(this.elem,2*this.elem.length);}this.elem[this.top]= e;
top++;}publicEpeek(){if(this.top <=0){thrownewStackOverflowError("栈为空!");}returnthis.elem[this.top -1];}publicEpop(){if(this.top <=0){thrownewStackOverflowError("栈为空!");}this.top--;returnthis.elem[this.top];}publicbooleanempty(){returnthis.top <=0;}@OverridepublicStringtoString(){if(this.top <=0){return"[]";}StringBuilder stringBuilder =newStringBuilder("[");for(int i =0; i <this.top -1; i++){
stringBuilder.append(this.elem[i]);
stringBuilder.append(",");}
stringBuilder.append(this.elem[this.top -1]);
stringBuilder.append("]");return stringBuilder.toString();}}
测试代码:
publicclassTest{publicstaticvoidmain(String[] args){MyStack<Integer> stack1 =newMyStack<>();MyStack<String> stack2 =newMyStack<>();//push test
stack1.push(1);
stack1.push(2);
stack1.push(3);System.out.println(stack1.toString());
stack2.push("虎年");
stack2.push("大吉");System.out.println(stack2.toString());//peek testSystem.out.println(stack1.peek());System.out.println(stack2.peek());//pop test empty testSystem.out.println(stack1.pop());System.out.println(stack1.pop());System.out.println(stack1.pop());System.out.println(stack1.empty());System.out.println(stack2.pop());System.out.println(stack2.pop());System.out.println(stack2.empty());}}
运行结果:
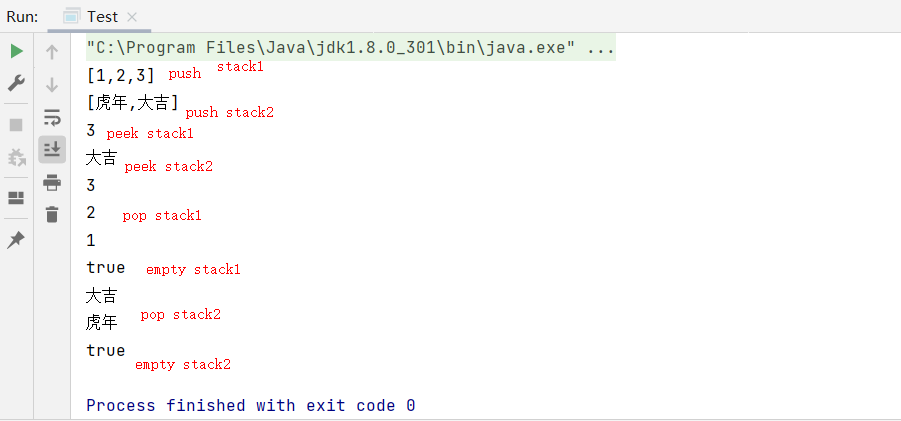
2.3使用Stack解决问题
2.3.1验证栈的出入序列
在前面1.2.1已经介绍了给定一个入栈序列,判断一个序列是否可能是出栈序列的问题,在这里我们来尝试使用编程来解决它!
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如,序列 {1,2,3,4,5} 是某栈的压栈序列,序列 {4,5,3,2,1} 是该压栈序列对应的一个弹出序列,但 {4,3,5,1,2},就不可能是该压栈序列的弹出序列。
示例:
输入:pushed =[1,2,3,4,5], popped =[4,5,3,2,1]
输出:true
解释:我们可以按以下顺序执行:
push(1),push(2),push(3),push(4),pop()->4,push(5),pop()->5,pop()->3,pop()->2,pop()->1
输入:pushed =[1,2,3,4,5], popped =[4,3,5,1,2]
输出:false
解释:1 不能在 2 之前弹出
提示:
0
<
=
p
u
s
h
e
d
.
l
e
n
g
t
h
=
=
p
o
p
p
e
d
.
l
e
n
g
t
h
<
=
1000
0 <= pushed.length == popped.length <= 1000
0<=pushed.length==popped.length<=1000
0
<
=
p
u
s
h
e
d
[
i
]
,
p
o
p
p
e
d
[
i
]
<
1000
0 <= pushed[i], popped[i] < 1000
0<=pushed[i],popped[i]<1000
pushed 是 popped 的入栈排列。
💡解题思路:
我们可以对入栈序列数组进行遍历,每次都将里面的元素入栈,然后依次按顺序将出栈序列数组中的元素与栈顶元素比较,如果相等就出栈,并比较下一个出栈数组元素与下一次栈顶元素是否相等,相等就出栈,以此类推直到不相等为止,最终栈为空栈,则出栈序列是可能的。
例如:
p
u
s
h
e
d
=
[
1
,
2
,
3
,
4
,
5
]
,
p
o
p
p
e
d
=
[
4
,
5
,
3
,
2
,
1
]
pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
pushed=[1,2,3,4,5],popped=[4,5,3,2,1]
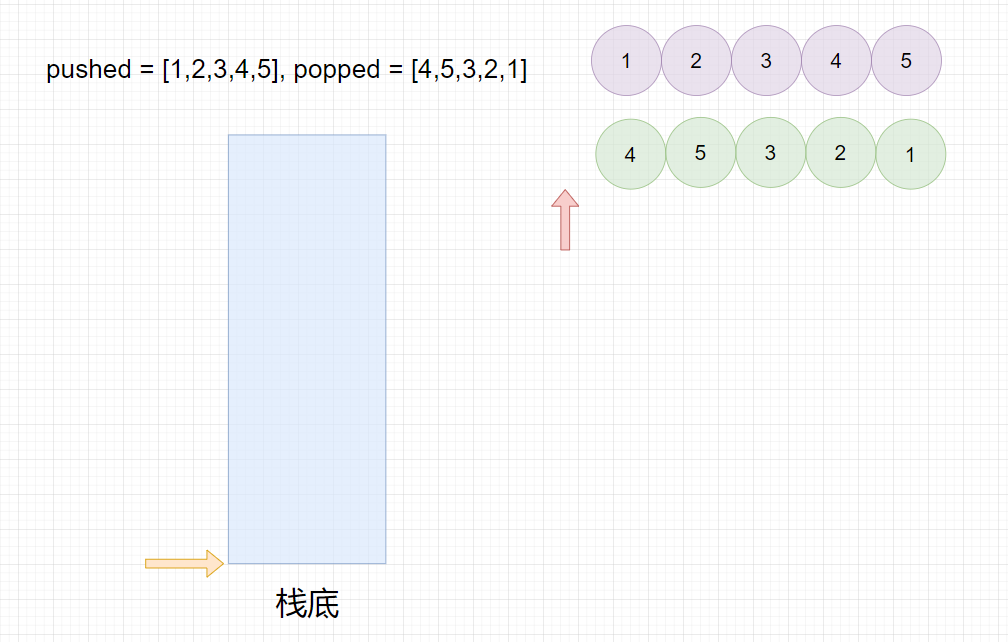
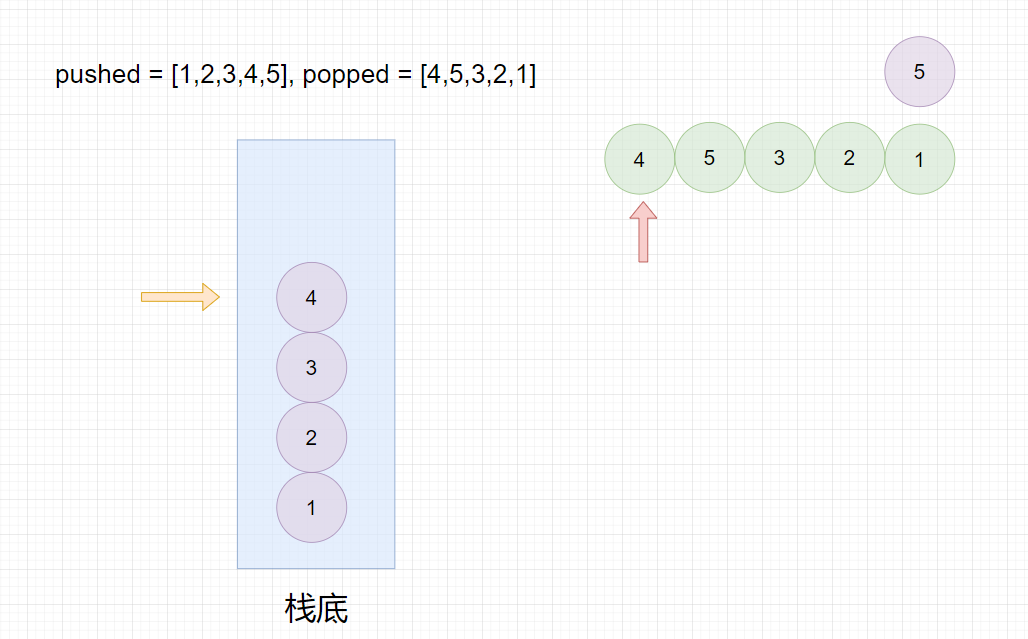
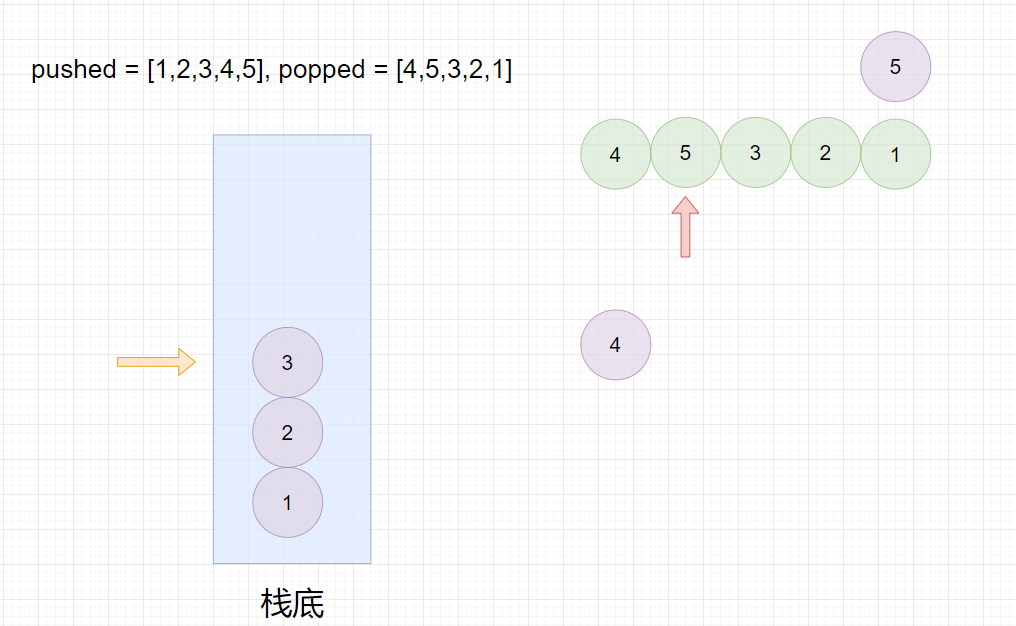
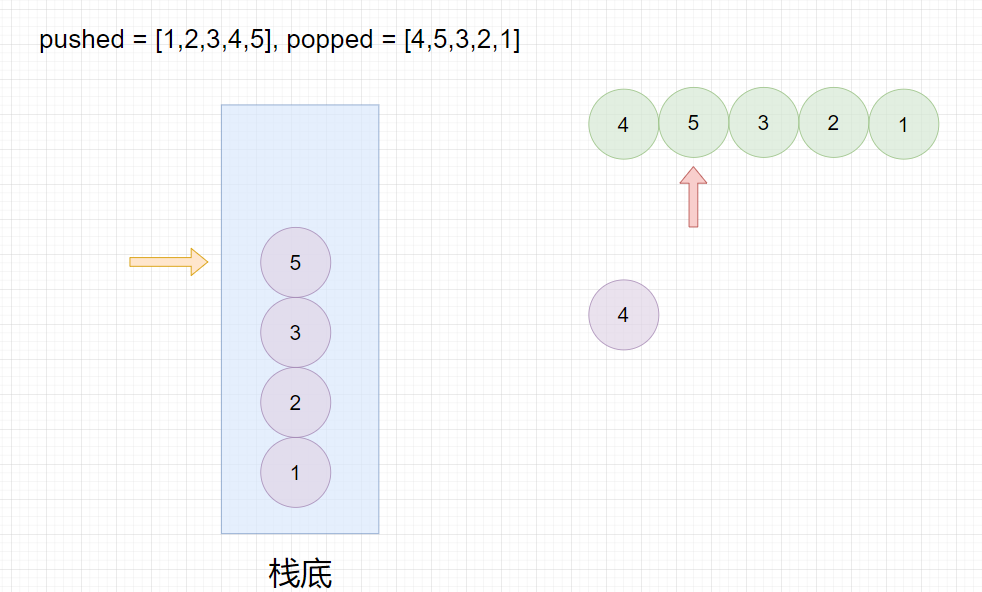
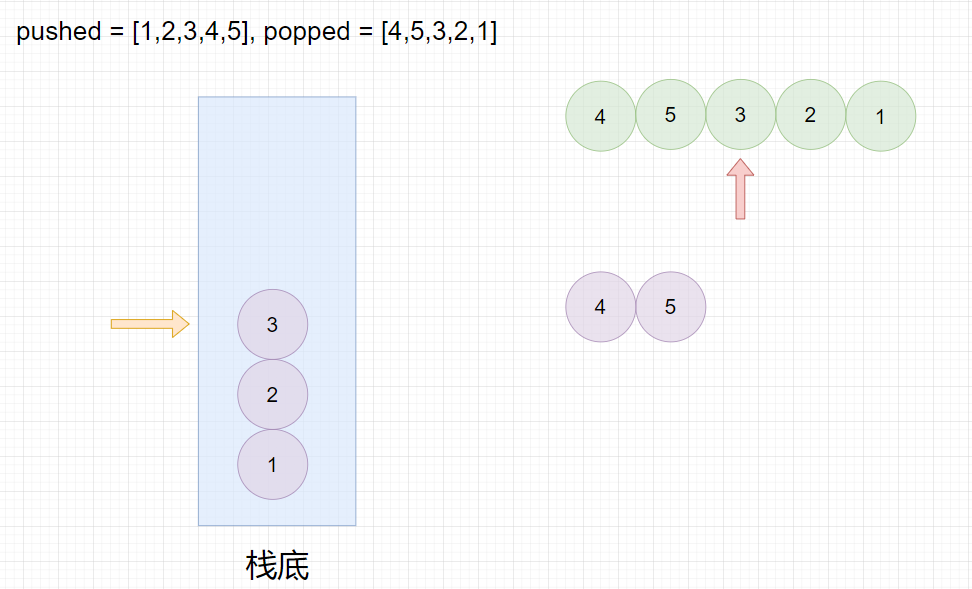
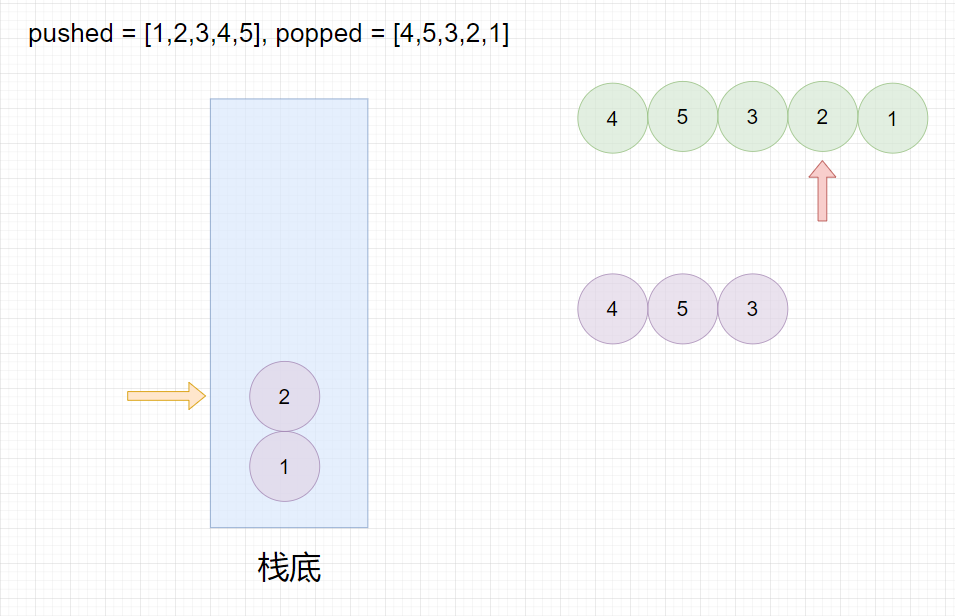
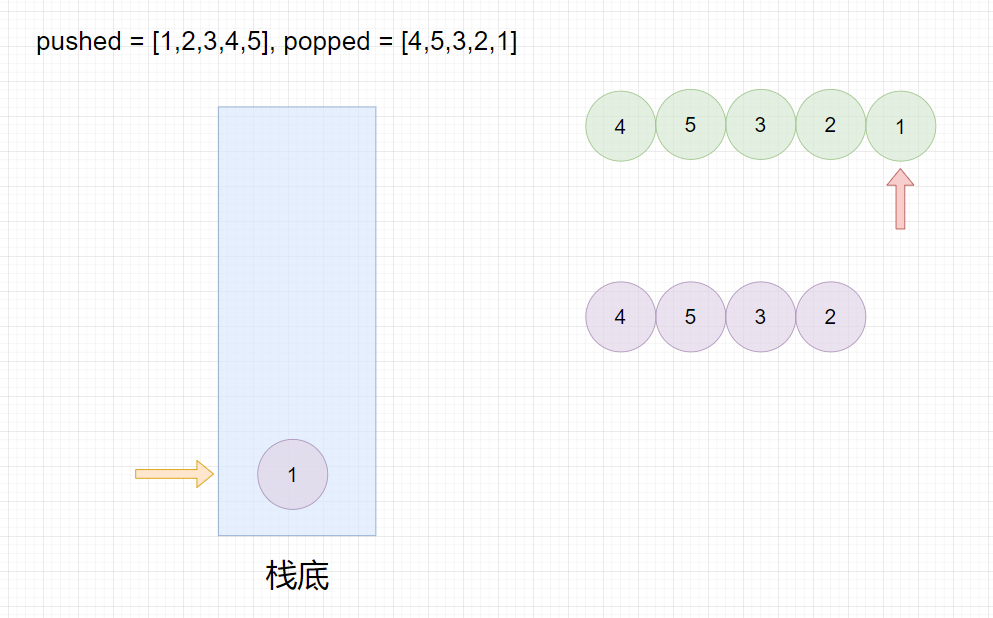
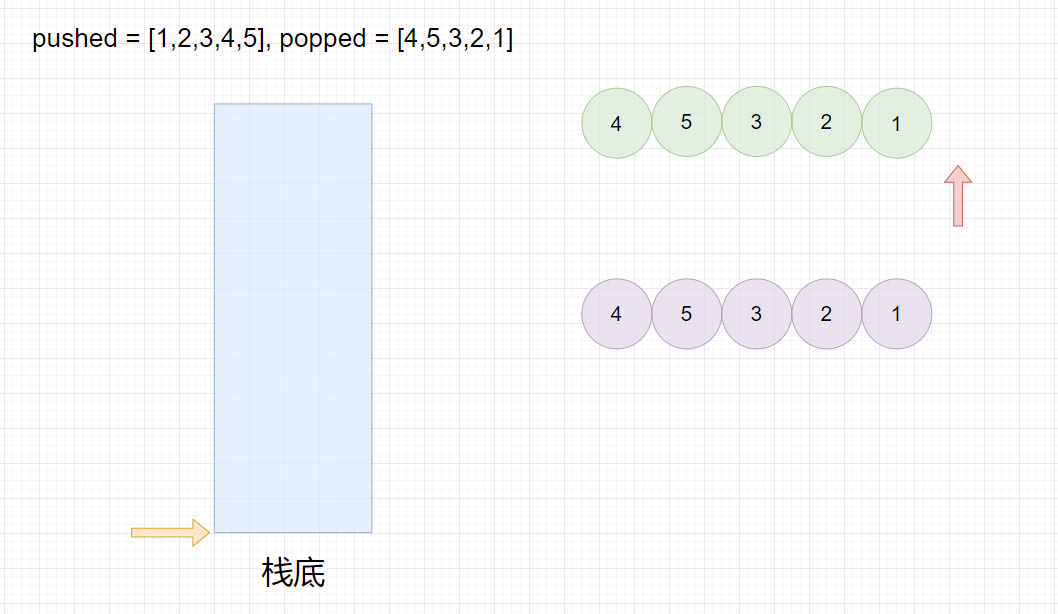
最终栈为空,所以返回
true
。
🔑源代码:
classSolution{publicbooleanvalidateStackSequences(int[] pushed,int[] popped){Stack<Integer> stack =newStack<>();int j =0;for(int i =0; i < pushed.length; i++){
stack.push(pushed[i]);while(!stack.empty()&& stack.peek()== popped[j]){
stack.pop();
j++;}}return stack.empty();}}
在线练习链接:
1.946. 验证栈序列
2.剑指 Offer 31. 栈的压入、弹出序列
2.3.2逆波兰表达式
还能记得文章前面介绍的前中后缀表达式吗?逆波兰表达式就是后缀表达式,我们来尝试一下使用编程进行后缀表达式求值。
根据 逆波兰表示法,求表达式的值。
有效的算符包括 +、-、*、/ 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。
说明:
整数除法只保留整数部分。
给定逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
示例 1:
输入:tokens =["2","1","+","3","*"]
输出:9
解释:该算式转化为常见的中缀算术表达式为:((2+1)*3)=9
示例 2:
输入:tokens =["4","13","5","/","+"]
输出:6
解释:该算式转化为常见的中缀算术表达式为:(4+(13/5))=6
示例 3:
输入:tokens =["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出:22
解释:
该算式转化为常见的中缀算术表达式为:
((10*(6/((9+3)*-11)))+17)+5=((10*(6/(12*-11)))+17)+5=((10*(6/-132))+17)+5=((10*0)+17)+5=(0+17)+5=17+5=22
提示:
1
<
=
t
o
k
e
n
s
.
l
e
n
g
t
h
<
=
104
1 <= tokens.length <= 104
1<=tokens.length<=104
tokens[i]
要么是一个算符("+"、"-"、"*" 或 “/”),要么是一个在范围
[-200, 200]
内的整数
逆波兰表达式:
逆波兰表达式是一种后缀表达式,所谓后缀就是指算符写在后面。
平常使用的算式则是一种中缀表达式,如
(
1
+
2
)
∗
(
3
+
4
)
( 1 + 2 ) * ( 3 + 4 )
(1+2)∗(3+4) 。
该算式的逆波兰表达式写法为
(
(
12
+
)
(
34
+
)
∗
)
( ( 1 2 + ) ( 3 4 + ) * )
((12+)(34+)∗) 。
逆波兰表达式主要有以下两个优点:
去掉括号后表达式无歧义,上式即便写成
12
+
34
+
∗
1 2 + 3 4 + *
12+34+∗ 也可以依据次序计算出正确结果。
💡解题思路:
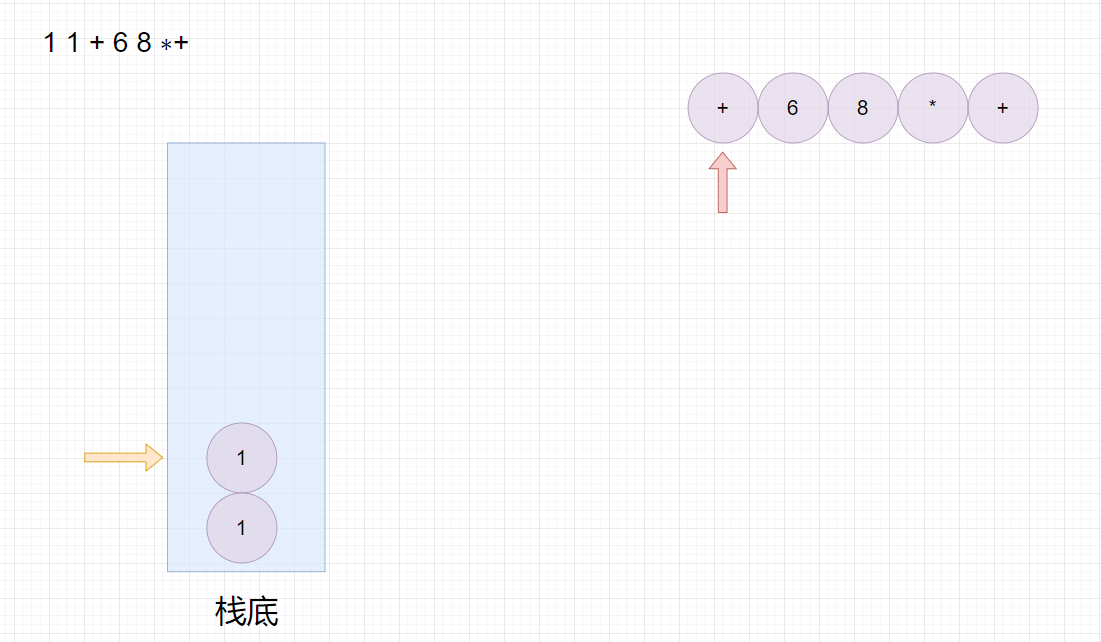
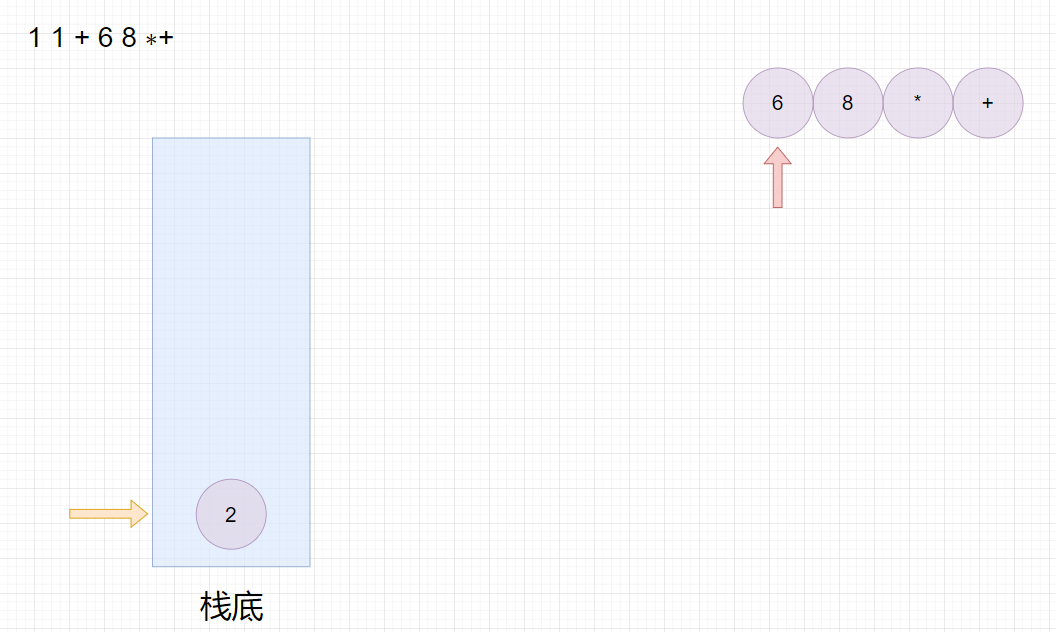
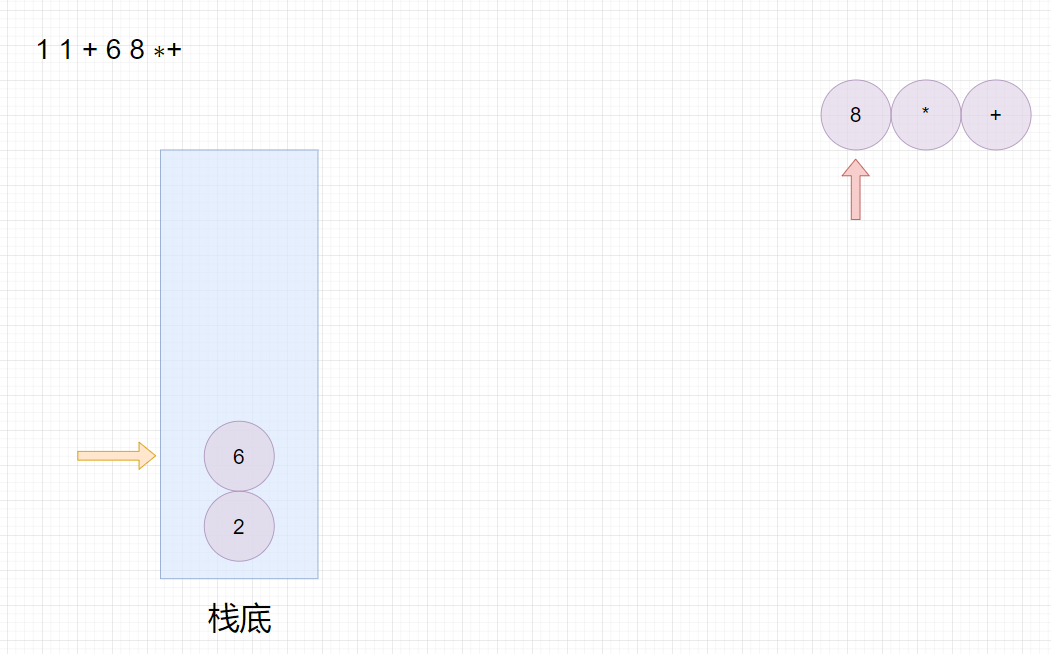
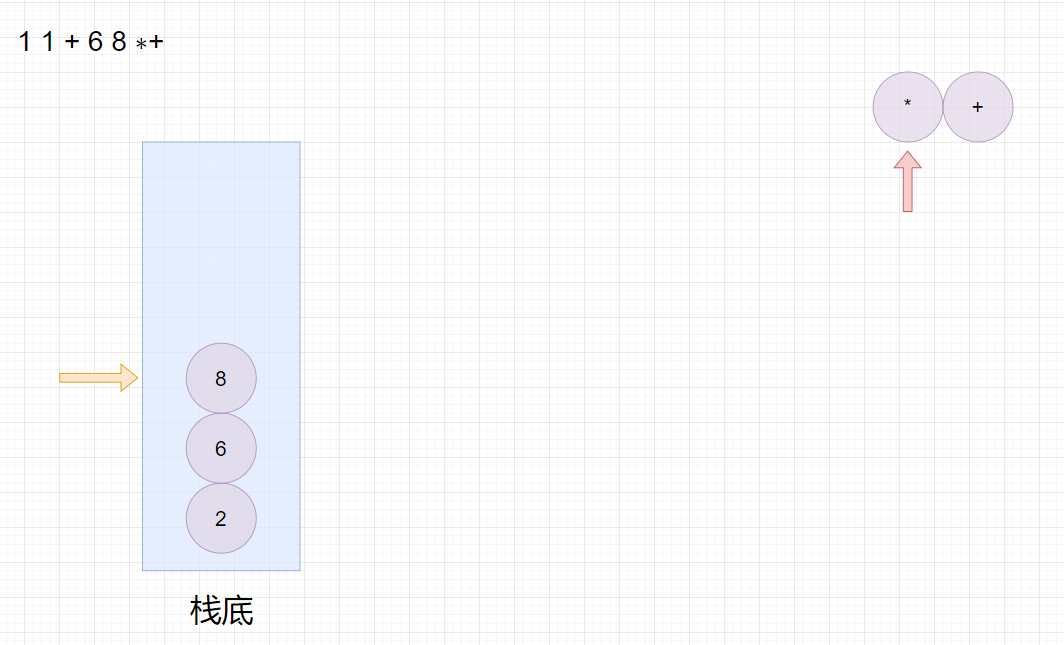
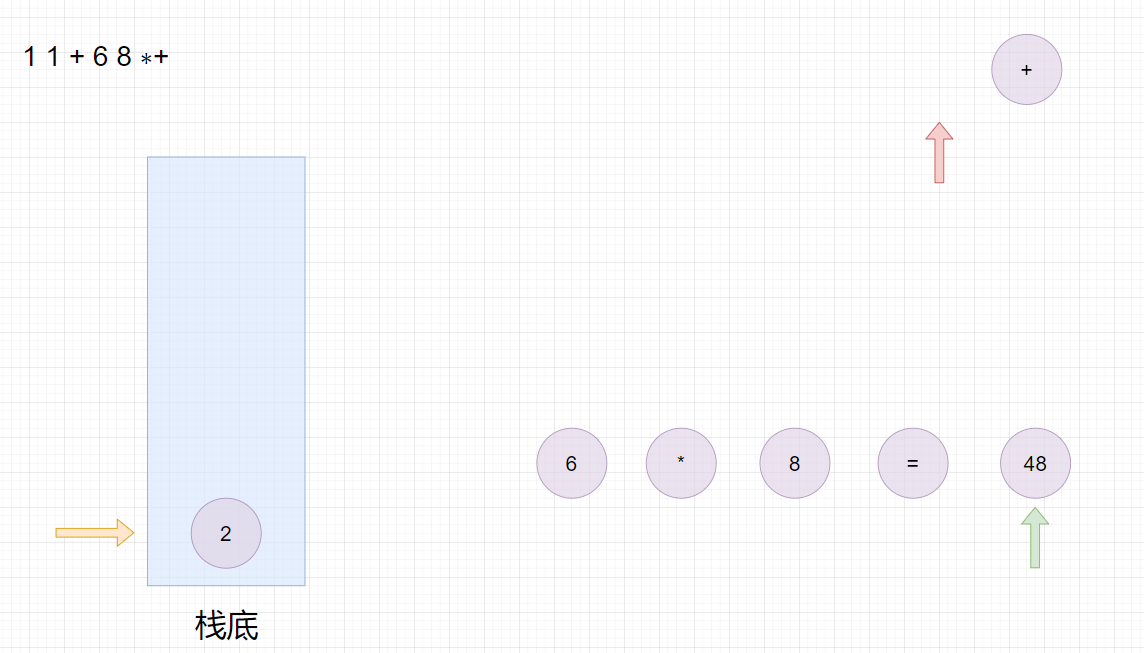
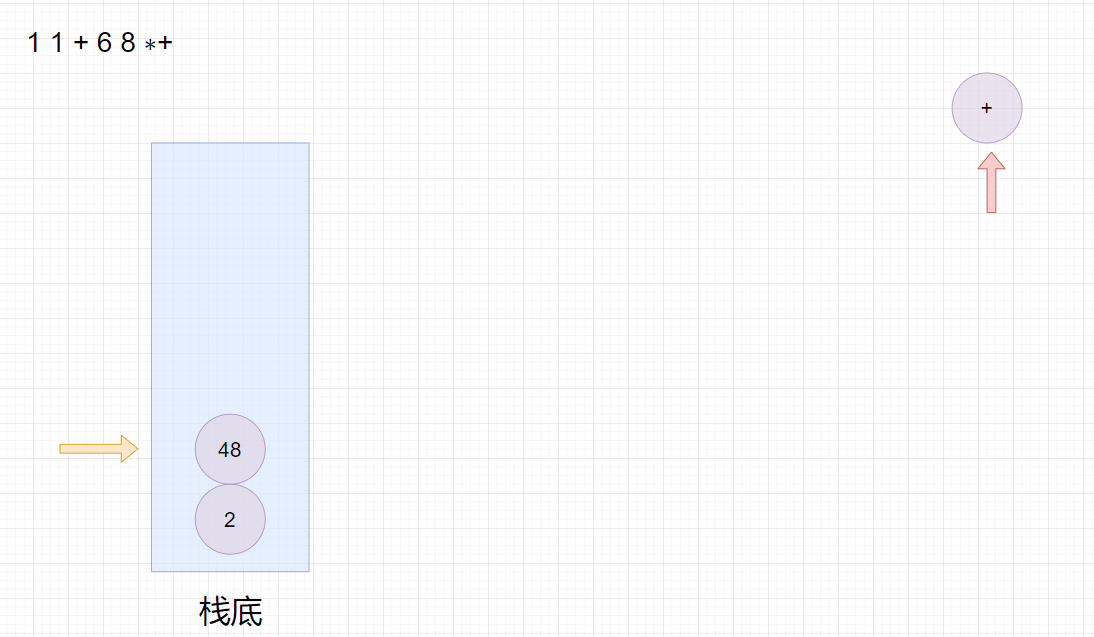
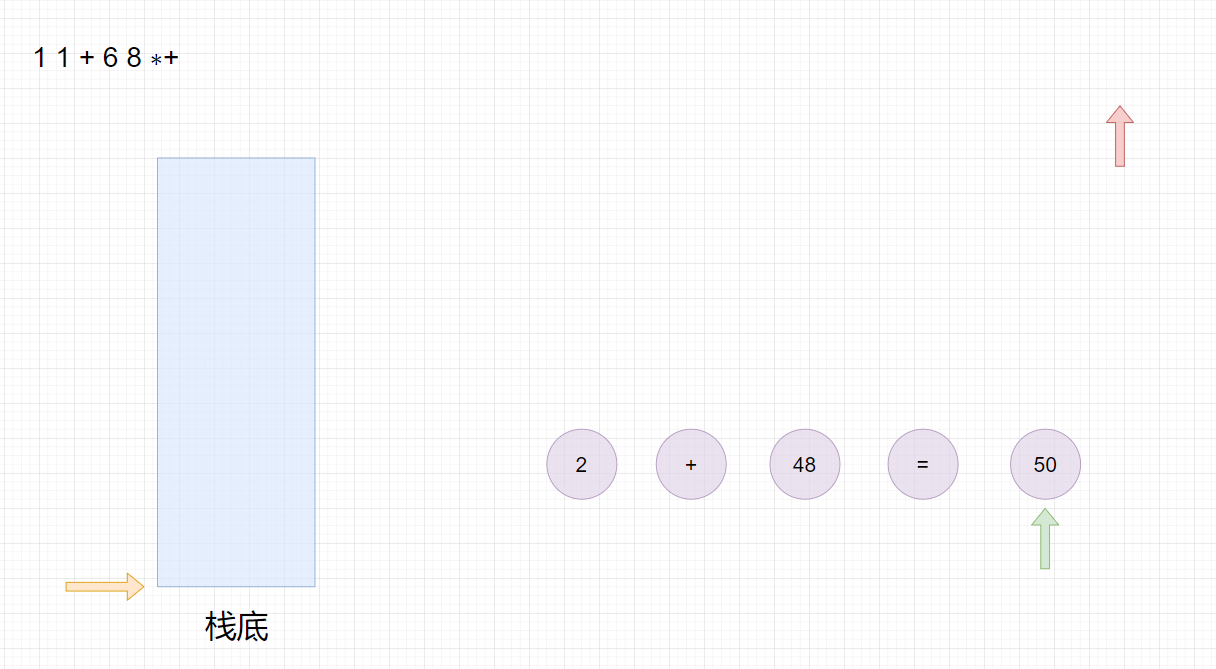
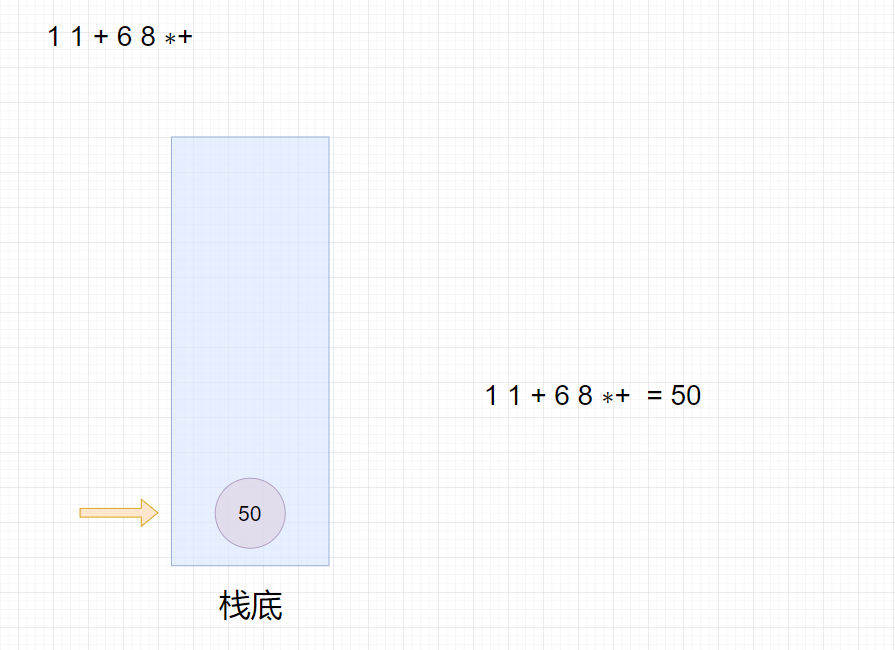
适合用栈操作运算:遇到数字则入栈;遇到运算符则取出栈顶两个数字进行计算,并将结果压入栈中。
首先遍历字符串数组,然后判断元素是否是运算符,如果是则从栈中取出两个元素进行运算,并将结果入栈,如果不是运算符则将字符串转数字入栈。
注意,先出栈的数要放在运算符右边,后出栈的数放在运算符左边。
最终栈顶元素的值即为运算结果。
比如:
11
+
68
∗
+
1 1 + 6 8 ∗+
11+68∗+,转换成中缀表达式为
1
+
1
+
6
∗
8
1 + 1 + 6 ∗8
1+1+6∗8,结果为
50
50
50。
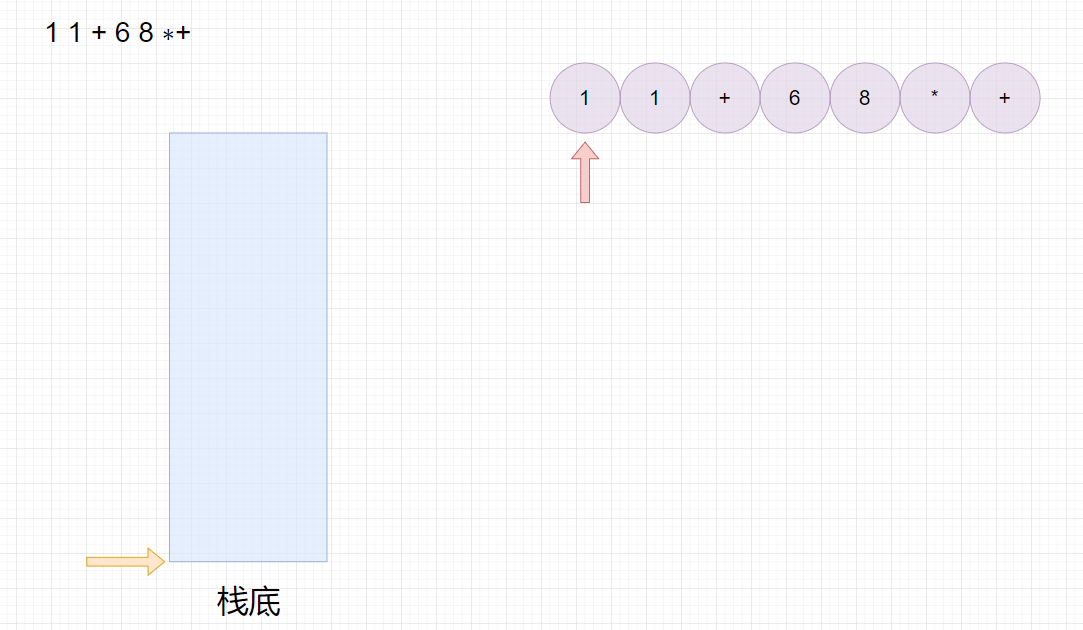
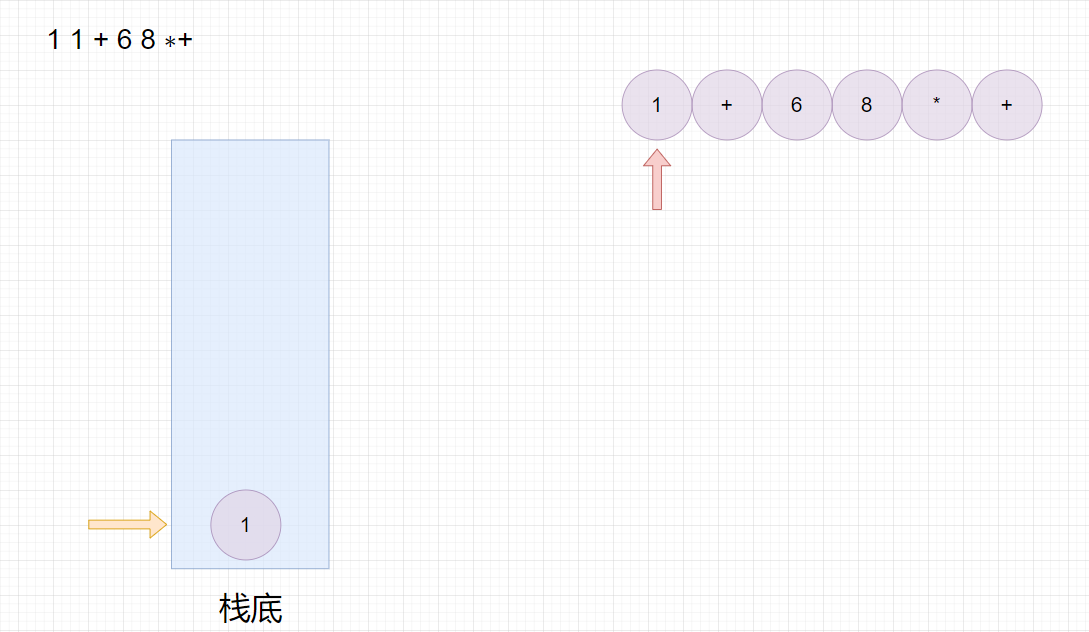

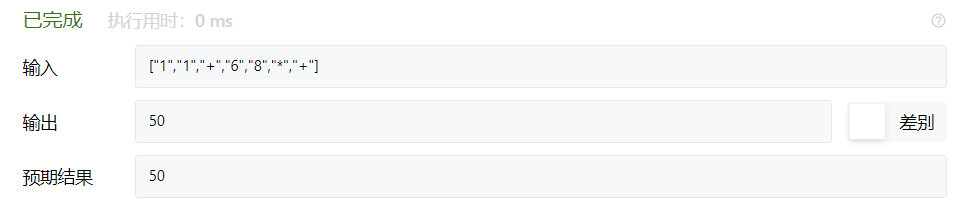
🔑源代码:
classSolution{publicintevalRPN(String[] tokens){Stack<Integer> stack =newStack<>();for(int i =0; i < tokens.length; i++){String s = tokens[i];if(isOperation(s)){//遇到运算符,出栈元素,进行计算,结果入栈int num2 = stack.pop();int num1 = stack.pop();switch(s){case"+":
stack.push(num1 + num2);break;case"-":
stack.push(num1 - num2);break;case"*":
stack.push(num1 * num2);break;case"/":
stack.push(num1 / num2);break;}}else{//遇到数字,入栈,等待计算
stack.push(Integer.parseInt(s));}}//最终栈中的元素为最终结果return stack.pop();}publicbooleanisOperation(String s){if(s.equals("+")|| s.equals("-")|| s.equals("*")|| s.equals("/")){returntrue;}else{returnfalse;}}}
在线练习链接:
150. 逆波兰表达式求值
剑指 Offer II 036. 后缀表达式
2.3.3最小栈
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
push(x) —— 将元素 x 推入栈中。
pop() —— 删除栈顶的元素。
top() —— 获取栈顶元素。
getMin() —— 检索栈中的最小元素。
示例:
输入:
["MinStack","push","push","push","getMin","pop","top","getMin"][[],[-2],[0],[-3],[],[],[],[]]
输出:
[null,null,null,null,-3,null,0,-2]
解释:
MinStack minStack =newMinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();--> 返回 -3.
minStack.pop();
minStack.top();--> 返回 0.
minStack.getMin();--> 返回 -2.
提示:
pop、top 和 getMin 操作总是在 非空栈 上调用。
💡解题思路:
该题的意思是设计一个栈,能够获取栈中实时最小值,我们可以使用一个辅助栈,用来存放实时最小值,主栈每一个元素均。出栈时,如果辅助栈出栈元素与主栈出栈元素相同,则同时出栈,否则仅出主栈上的元素。
怎么在辅助栈中存放实时最小值?很简单,入栈时,如果待入栈元素的值小于或等于栈顶元素,则入栈,辅助栈为空栈时,直接入栈。
主栈不论什么情况,均入栈。
代码演示主栈为
stack
,辅助栈为
min
。
🔑源代码:
classMinStack{Stack<Integer> stack;Stack<Integer> min;publicMinStack(){this.min =newStack<>();this.stack =newStack<>();}publicvoidpush(int val){if(this.min.isEmpty()){this.min.push(val);}elseif(this.min.peek()>= val){this.min.push(val);}this.stack.push(val);}publicvoidpop(){if(this.stack.peek().equals(this.min.peek())){this.min.pop();}this.stack.pop();}publicinttop(){returnthis.stack.peek();}publicintgetMin(){returnthis.min.peek();}}
在线练习链接:
155. 最小栈
面试题 03.02. 栈的最小值
好了,本文就分享到这里了,下次再见!
觉得文章写得不错的老铁们,点赞评论关注走一波!谢谢啦!
版权归原作者 未见花闻 所有, 如有侵权,请联系我们删除。