SVM模型详解

入门小菜鸟，希望像做笔记记录自己学的东西，也希望能帮助到同样入门的人，更希望大佬们帮忙纠错啦~侵权立删。

一、SVM定义与解决目标

SVM是一个二类分类器。其基本模型定义为特征空间上的间隔最大的线性分类器，其学习策略便是间隔最大化，最终可转化成一个凸二次规划问题的求解。即找到一个超平面，使两类数据离超平面越远越好，这样就可以让模型对新的数据分类更准确，即分类器更加稳定。

🎈支持向量：离分隔超平面最近的一些点

🎈间隔最大化：寻找最大化支持向量到分隔超平面的距离，以此为目标来求出分隔超平面

🎈数据分类的类别

（1）线性可分

（2）线性不可分

二、SVM算法原理

1、线性可分

分为2种：无松弛变量和带松弛变量

以2个特征为例：

如下图所示：如何分类黑点点和红点点，我们直观来看粉色那条线作为分界最好（因为该超平面对训练样本局部扰动的容忍性最好，即稳定性更高）

🌳原始待分类的数据：(x11,x12,y1)，……，(xm1,xm2,ym)

x1,x2就是不同维的特征

y的取值为1或-1（因为2分类）

🌳目标超平面： $w^{T}X+b = 0$ —— 求最优w和b

(这里其实展开就是 $w_{1}x_{1} + w_{2}x_{2}+b=0$ ；

w是法向量，决定了超平面的方向；

b是位移项，决定了超平面与原点间的距离）

🌳那么空间中任意一点(x1,x2)到目标超平面的距离则为：

$r=\frac{\left|\omega^{T} x+b\right|}{|| \omega||}$

🌳又有定义：（其中 $x^{(i)}$ 和 $y^{(i)}$ 分别是第i个样本和第i个样本值所对应的目标值）

$y_{i}(w^{T}x_{i} + b),i=1,.....,m$ 为函数距离；

所以我们把函数距离和点到面的距离进行一个综合，就变成了：

$\min\frac{y^{(i)}\left(w^{T} x^{(i)}+b\right)}{\|w\|}, i=1, \ldots, m$ 为数据集与分隔超平面的几何距离；

（1）这里用几何距离而不用函数距离的原因：

当w,b成倍增加时，函数距离也会相应的成倍的增加，但几何函数则不会

（2）我们刚刚不是说y的取值是1或-1嘛，这就保证了如果样本分类正确，则这个值是一个正数；如果样本分类错误，这个值是一个负数。这很好理解，分类对了就是同一边，就是正数嘛，即公式如下：

$\left\{\begin{array}{ll} \omega^{T} x_{i}+b>0, & y_{i}=+1 \\ \omega^{T} x_{i}+b<0, & y_{i}=-1 \end{array}\right.$

🌳但如果只以 $w^{T}X+b = 0$ 来划分，那么它的容错性可能不是很好，所以SVM这里引入了这个：

$\left\{\begin{array}{ll} \omega^{T} x_{i}+b>=1, & y_{i}=+1 \\ \omega^{T} x_{i}+b<=-1, & y_{i}=-1 \end{array}\right.$

如图所示：（图里的转置符号我就懒得写上去了嘻嘻）

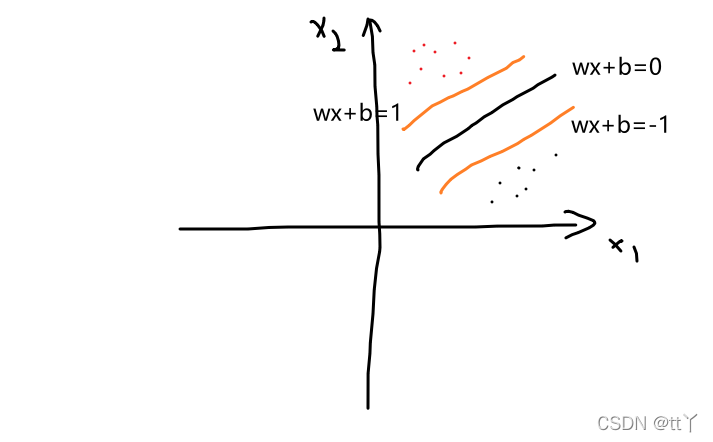
🌳间隔

其中，支持向量使上式的等号成立。两个异类支持向量到超平面的距离之和，也称为间隔**:**

$\gamma=\frac{2}{\|\omega\|}$ (其实就是那两条橙色的线的距离）

🌳最大间隔划分超平面

所以我们要找到对应的w和b让 $\gamma$ 最大，即以下公式：

$\max _{\omega, b} \frac{2}{\|\omega\|}, s . t . y_{i}\left(\omega^{T} x_{i}+b\right) \geq 1, i=1,2, \ldots, m$

条件由以下所得：

$\left\{\begin{array}{ll} \omega^{T} x_{i}+b>=1, & y_{i}=+1 \\ \omega^{T} x_{i}+b<=-1, & y_{i}=-1 \end{array}\right.$ 左右乘上 $y_{i}$

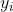
（1）无松弛变量

🌳由上式进行变式

为了最大化间隔，仅需最大化 $\frac{1}{\|\omega\|}$ ，这等价于最小化 $\|\omega\|^2$

$\min _{\omega, b} \frac{\|\omega\|^2}{2}, s . t . y_{i}\left(\omega^{T} x_{i}+b\right) \geq 1, i=1,2, \ldots, m$

这就是SVM的基本型

🌳我们把约束条件融合到优化目标函数中，建立拉格朗日公式

$L(w, b, \alpha)=\frac{1}{2}\|w\|^{2}+\sum_{i=1}^{m} \alpha_{i}\left(1-y_{i}\left(w^{T} x_{i}+b\right)\right)$

令 L(w,b,α)对 w和b的偏导为零，得到：

$w =\sum_{i=1}^{m} \alpha_{i} y_{i} x_{i}$ $\sum_{i=1}^{m} \alpha_{i} y_{i} = 0$

代入L得

$\max _{\alpha} \sum_{i=1}^{m} \alpha_{i}-\frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j} x_{i}^{T} x_{j} --s.t. \sum_{i=1}^{m} \alpha_{i} y_{i}=0, \alpha_{i} \geq 0, i=1,2, \ldots, m$

解出 $\alpha$ 后代入得：

（这里的x和y都是支持向量）

（2）带松弛变量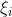 $\xi_{i}$ 和惩罚因子C

$\min \frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{n} \xi_{i} -- s . t . y_{i}\left(\omega^{T} x_{i}+b\right) \geq 1-\xi_{i} , i=1,2, \ldots, m,\xi_{i}\geq0$

当C趋近于无穷大时，基本等价于无松弛变量的时候，当C取有限值的时允许一些样本不满足约束。

其余与上述一样

2、线性不可分

如果训练样本线性不可分，那么只要样本的属性是有限个,就可以将其映射到高维特征空间，使这些样本线性可分。

Note：升维后不一定线性可分，不过一般情况下升维后会更接近线性可分

凡是遇到线性不可分的情况，一律映射到高维度空间，会出现维度爆炸的情况，那么计算难度会很大的。此时我们可以使用核函数来简化计算，核函数虽然也是将特征进行从低维到高维的转化但是是在低维上进行计算而实际的效果表现在高维上解决了维度爆炸的问题

（1）核函数定义和应用背景

只要一个对称函数所对应的核矩阵半正定，它就能作为核函数使用。

但是在不知道特征映射的形式时，我们并不知道什么样的核函数才是合适的。因此，核函数的选择成为SVM的最大变数。

构建核函数首先要确定输入空间到特征空间的映射，想要获取输入空间到映射空间的映射，我们需要明确输入空间内数据的分布情况，但大多数情况下，我们并不知道自己所处理的数据的具体分布，故一般很难构造出完全符合输入空间的核函数，因此我们用几种常用的核函数来代替自己构造核函数

（2）线性核函数 LINEAR

$k(x,x_{i}) = x * x_{i}$ （内积）

LINEAR主要用于线性可分的情况。我们可以看到特征空间到输入空间的维度是一样的，其参数少，速度快。对于线性可分数据，其分类效果很理想，因此我们通常首先尝试用线性核函数来做分类，看看效果如何，如果不行再换别的。

（3）高斯径向基核函数 RBF

$k(x, x i)=\exp \left(-\frac{\|x-x i\|^{2}}{\delta^{2}}\right)$

它是一种局部性强的核函数，其可以将一个样本映射到一个更高维的空间，它是应用最广的一个，无论大样本还是小样本都有比较好的性能，而且其相对于多项式核函数参数要少，因此大多数情况下在不知道用什么核函数的时候，优先使用高斯核函数

（4）多项式核函数 POLY

$k(x,x_{i}) = ((x * x_{i})+1)^{d}$

它也可以实现将低维的输入空间映射到高维的特征空间。但多项式核函数的参数多，当多项式的阶数比较高的时候，核矩阵的元素值将趋于无穷大或者无穷小，计算复杂度会大到无法计算

（5）神经元的非线性作用核函数 Sigmoid

关于Sigmoid函数的介绍可以看往期文章中

基于分层softmax的CBoW模型详解_tt丫的博客-CSDN博客_分层softmax中有关逻辑回归Sigmoid函数的讲解

$k\left(x, x_{i}\right)=\tanh \left(\eta<x, x_{i}>+\theta\right)$

这样SVM实现的就是一种多层神经网络

（6）核函数选择技巧

如果我们对数据有个初步的分布了解等等，就根据这些特点去选择核函数

如果我们不清楚的话，可以使用交叉验证的方法来试用不同的核函数，误差最小的就是效果最好的核函数；或者也可以将多个核函数结合起来，形成混合核函数。

如果特征的数量大到和样本数量差不多，则选用线性核SVM；

如果特征的数量小，样本的数量正常，则选用高斯核函数SVM；

如果特征的数量小，而样本的数量很大，则需要手工添加一些特征从而变成第一种情况。

三、SVM代码实现

我们可以调用sklearn库中的SVM

比如说

model=sklearn.svm.SVC(C=2,kernel='rbf',gamma=10,decision_function_shape='ovo')

参数说明：

（1）C：C-SVC的惩罚参数C默认是1.0。C越大，相当于惩罚松弛变量，希望松弛变量接近0，即对误分类的惩罚增大，这样对训练集测试时准确率很高，但相对的，模型的泛化能力就会变弱。C值小，对误分类的惩罚减小，允许容错，将他们当成噪声点，泛化能力较强。

（2）kernel ：核函数，默认是rbf，可以是

0 —— 'linear'；1 —— 'poly'；2 —— 'rbf'；3 —— 'sigmoid'

（3）degree ：多项式poly函数的维度，默认是3，选择其他核函数时会被忽略

（4）gamma ：'rbf'，'poly'和'sigmoid'的核系数。当前默认值为'auto'，它使用1 / n_features，如果gamma='scale'传递，则使用1 /（n_features * X.std（））作为gamma的值。

（5）coef0 ：核函数的常数项。对于'poly'和 'sigmoid'有用

（6） tol ：默认为1e-3，停止训练的误差值大小

主要调节的参数有：C、kernel、degree、gamma、coef0

欢迎大家在评论区批评指正，谢谢~

标签： nlp 人工智能自然语言处理

本文转载自: https://blog.csdn.net/weixin_55073640/article/details/123726799
版权归原作者 tt丫 所有，如有侵权，请联系我们删除。

一、SVM定义与解决目标

二、SVM算法原理