YOLOv5深度剖析

目录

YOLOv5算法概述

   YOLOv5与历代YOLO算法相似，使用了网格的概念，将图像划分为多个网格，每个网格负责预测一个或多个物体，简单来说每个网格都可以产生预测框。网格可以产生预测框的原因也很简单。网格内存有几个（一般为三个）预测框的模板，也就是"anchor"每个anchor都有预设的宽高、坐标以及置信度。置信度表示网格内存在物体的概率。在训练过程中，真实的人工标注框的中点落在哪个在网格内，哪个网格内的anchor就会朝着这个真实框疯狂“生长”或者“萎缩”，并将置信度设为1，因为其存在物体，其他没有预测框的anchor置信度则为0。**如果把anchor与真实框之间宽高的差、坐标的差看成是均方差损失，把二元交叉熵作为置信度和类别的损失，那么目标检测问题就会大大简化为简单的回归预测和分类问题。**这就是YOLO算法的概述。

   历代YOLO算法都会提到网格这一概念，但值得注意的是，**这里的网格并不是真正意义上的网格，而是一个抽象的概念**。

    本文将会梳理YOLO算法的全部流程以及细节，深度剖析YOLO算法的原理。

网络结构

   YOLO v5的网络结构分为三部分：backbone骨干网络、neck颈部结构、head头部结构。

   在yolov5s.yaml文件中，作者将head与neck放在了一起。YOLOv5的网络结构为全卷积网络，即网络结构全由卷积、批归一化层等构成，不包含全连接层。YOLOv5模型结构图如下所示。

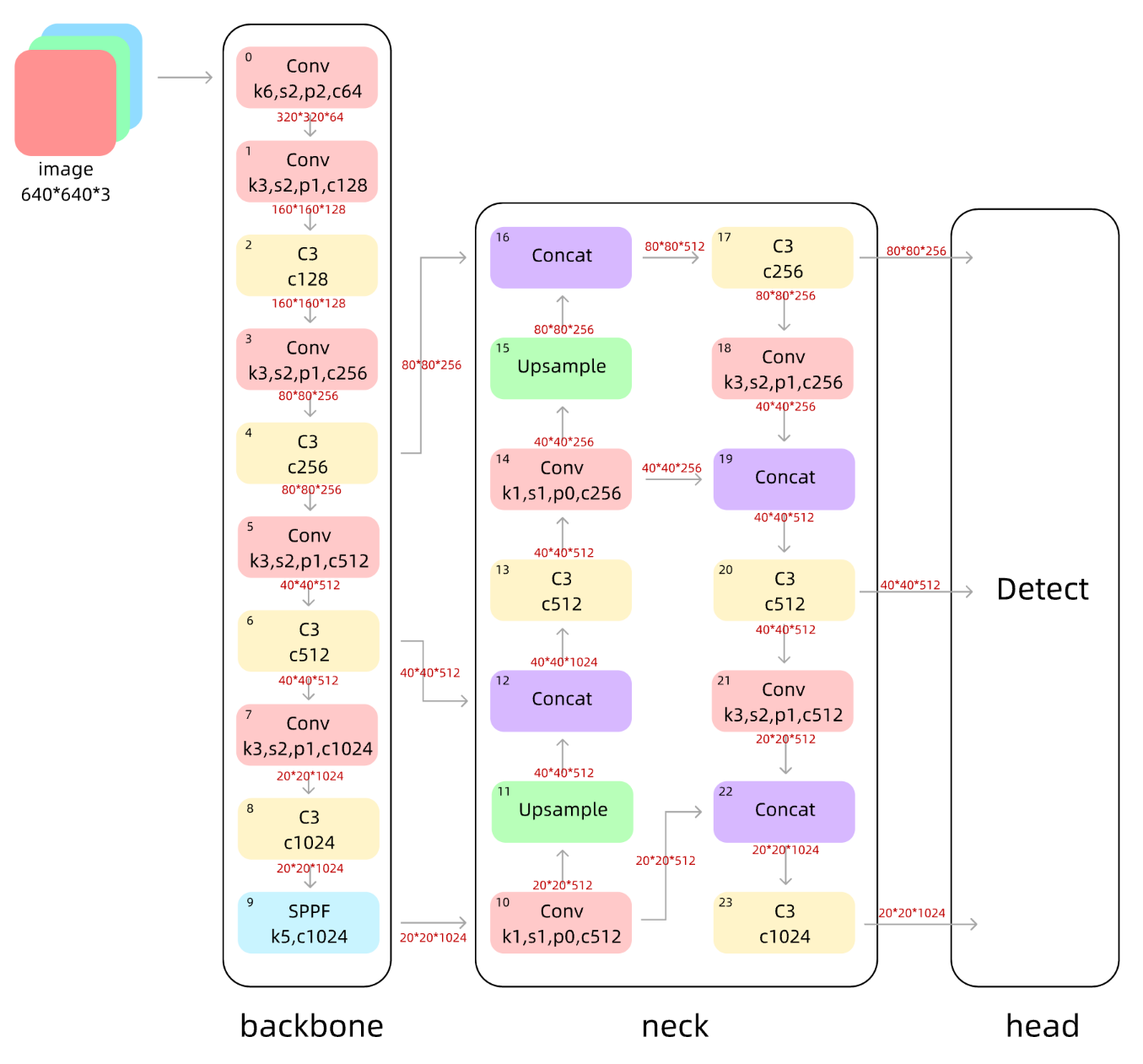
backbone

   backone骨干网络的主要作用就是提取特征，并不断缩小特征图。backbone中的主要结构有Conv模块、C3模块、SPPF模块。

Conv模块：

   由一个Conv2d、一个BatchNorm2d和激活函数构成。如下图所示。

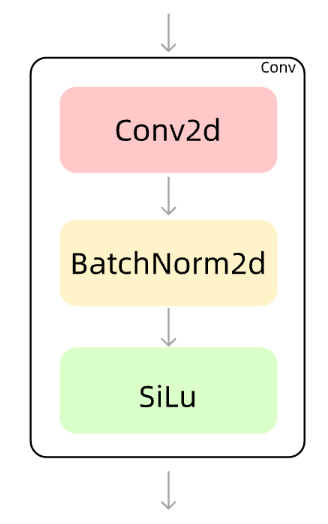
** Conv模块有提取特征并整理特征图的作用。**

   Conv模块中Conv2d的paddingg是自动计算的，通过修改stride来决定特征图缩小的倍数。在backbone中Conv模块的stride全部为2，kernel均为3。因此Conv每次会将特征图的宽高减半，下采样特征图，同时提取到目标特征。

   backbone以及neck均通过Conv模块对特征图进行升维或降维，并且存在许多1*1卷积。

   BatchNorm2d为批归一化层，对每批的数据做归一化，其详细作用不在这里赘述。

   SiLu为激活函数，增加了数据的非线性。

** 综上，Con可以提取特征和整理特征图。Conv模块完成了对特征图的下采样、升维降维、归一化、非线性等。**

C3模块

   C3由三个Conv模块和一个Bottleneck模块组成，得名C3。在backbone中，**C3是更为重要的提取特征的模块**。其结构图如下。

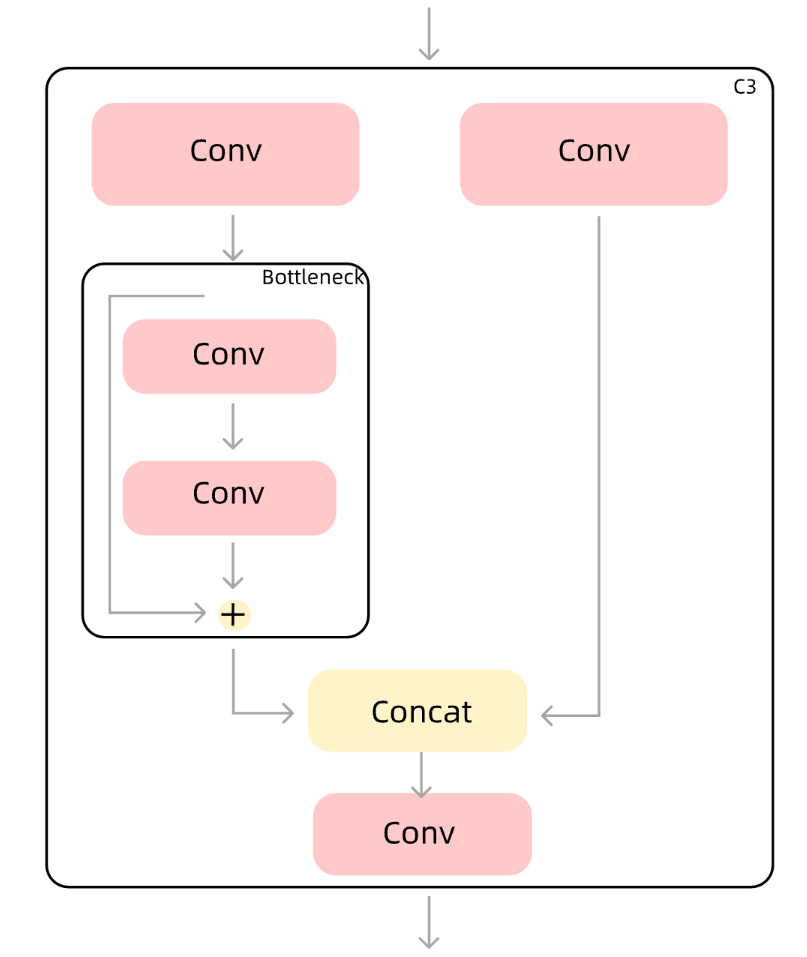
   特征图进入C3后，将会分为两路，左路经过Conv和一个Bottleneck，右路只经过一个Conv，最后将两路concat，再经过一个Conv。**C3中的3个Conv模块均为1*1卷积，**起到降维或升维的作用，对于提取特征意义不大。Bottleneck在backbone中使用的是残差连接，Bottleneck中有两个Conv，第一个Conv为1*1卷积，将通道缩减为原来的一半，第二个为3*3卷积，将通道数翻倍。**先降维有利于卷积核更好的理解特征信息，升维将有利于提取到更多更详细的特征**。最后使用残差结构，将输入与输出相加，避免梯度消失的问题。

SPPF

   SPP是空间金字塔池化，yolov5作者在SPP的基础上改进为SPPF，SPPF在输出相同的情况下速度更快。空间金字塔池化可以将尺度不固定的特征图，转为统一尺度。但是根据源码，在yolov5中SPP与SPPF通过padding，其实做的是same池化，前后特征图的大小是相等的。因此我认为，**SPPF在yolov5中的主要作用是融合多尺度特征。**将同一特征图不同尺度下的特征表现concat到一起。

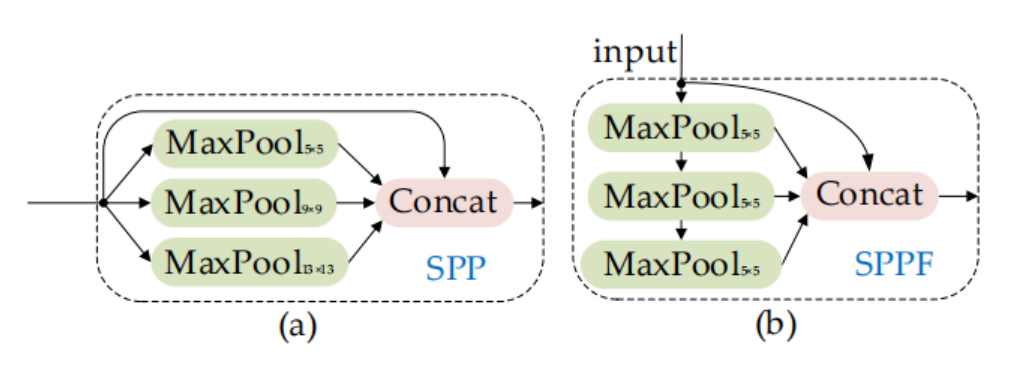
   图（a）所示为SPP，是将三个并行的MaxPool和输入concat到一起，第一个MaxPool的kernel为5*5，第二个为9*9，第三个为13*13。用三个不同大小的kernel，代表三个尺度。5*5的kernel可以理解为比较大的尺度，因为5*5取到的值会更多；而13*13就是比较小的尺度，因为大的kernel取到的值更少。这样就在图片的不同尺度下取到了最大的代表特征值，并concat融合。

   图（a）所示SPPF，是将三个kernel为5*5的MaxPool做串行计算，其实也好理解。第一个MaxPool表示较大的尺度，第二个MaxPool在第一个MaxPool的基础上进一步做池化，那么产生的尺度将会进一步缩小，第三个同理，这有点像感受野的概念，后文还会提到感受野。

   有实验证明，三个5*5，9*9，13*13的MaxPool并行，与三个5*5的MaxPool串行的结果完全一致。这也比较容易证明，这里不再赘述。至于为什么是9*9，13*13，我想是padding的原因。

neck

图形特征与语义特征

   在说Neck之前，我想先提两个概念：图形特征、语义特征。

   随着卷积的不断进行，神经网络提取到的特征越来越多，层次也越来越深。在卷积神经网络的浅层，网络提取到的特征也比较简单，**例如颜色、轮廓、纹理、形状等，这些特征仅体现在图形上，因而叫做图形特征**；而随着网络的不断加深，神经网络会对将这些特征不断融合、升维、产生新的特征，**例如颜色与纹理怎么组合，图片中哪里是天空，哪里是陆地，甚至包含一些人类不能理解的特征，这就叫做语义特征。**

** 图形特征是来自卷积神经网络浅层的特征，但只是简单的图形，语义性不够强；语义特征是来自卷积神经网络深层的特征，语义性强，但反而丢失了一些简单的图形。**

   而Neck结构就实现了浅层图形特征和深层语义特征的融合。

特征金字塔

   Neck结构其实是一个特征金字塔（FPN），把浅层的图形特征与浅层的语义特征结合在一起。

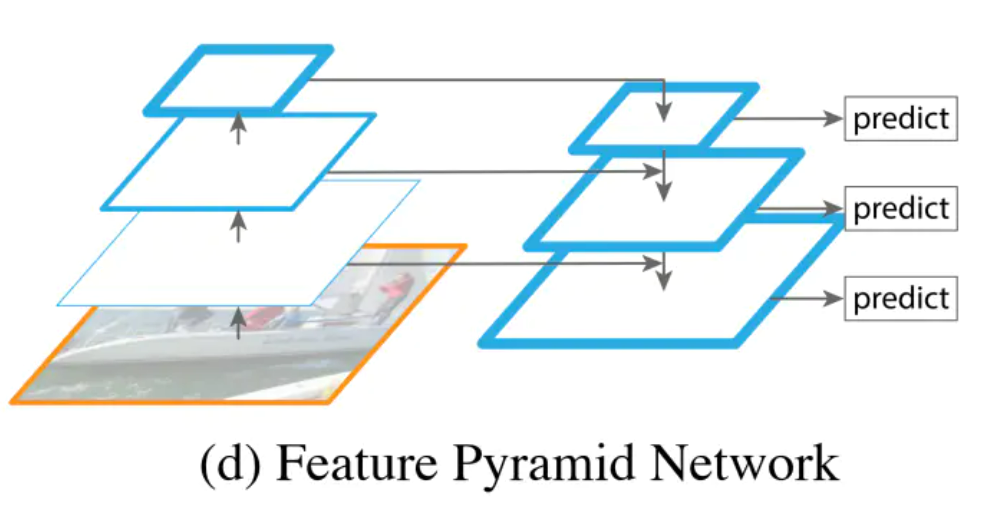
   YOLOv5的Neck从backbone中获取相对于较浅的特征，再与深层次的语义特征concat到一起。从图中可以看出，neck在左路通过Upsample上采样的方式，向特征图中插值，使特征图的尺度变大，以便于融合来自backbone的特征图，做特征的向上融合，特征图不断变大；neck的右路继续做下采样，一是为了获取不同尺度的特征图，二是使浅层的图形特征与深层的语义特征做更好的融合，而不仅仅是简单的concat。**neck层的作用就是将浅层的图形特征和深层的语义特征相结合，以获取更为完整的特征。**

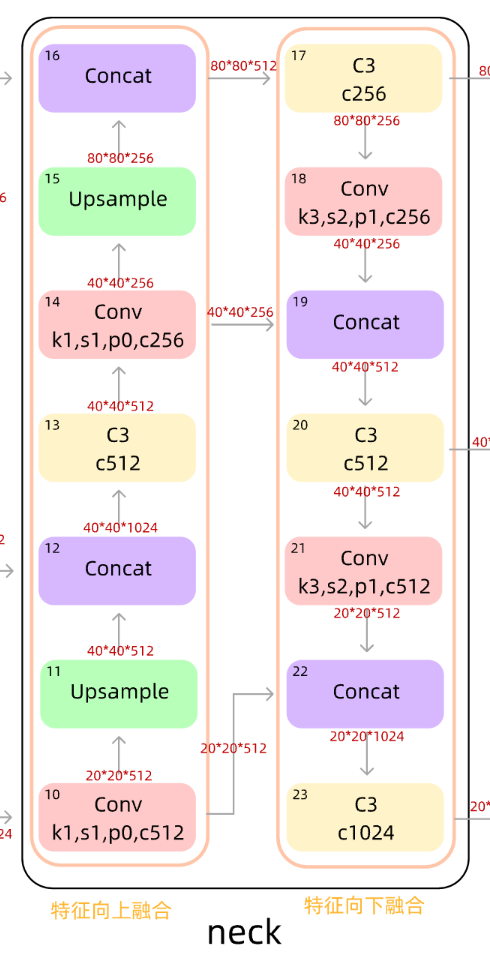
head

   head层为Detect模块，Detect模块的网络结构很简单，仅由三个1*1卷积构成，对应三个检测特征层。

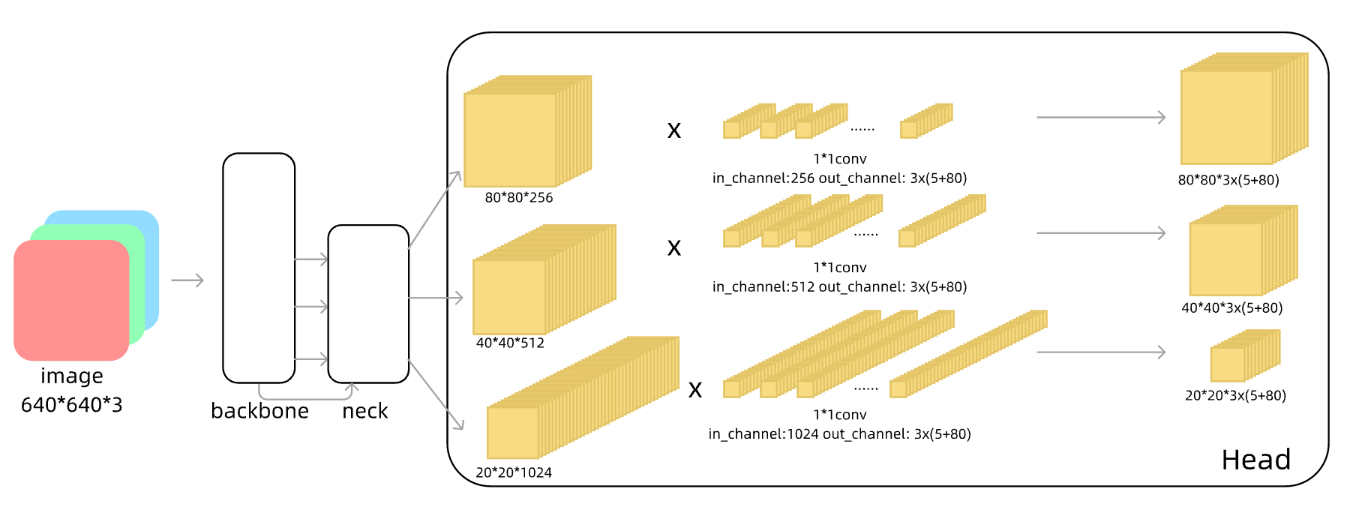
   1*1卷积的作用是升维或降维，1*1卷积核的通道数对应输入特征图的通道数，输出通道数对应卷积核的个数。一般情况1*1卷积不改变特征图的大小，但是会改变特征图的通道。

   先分析由neck输出的三张特征图：三张特征图分别为80*80*256，40*40*512，20*20*1024。**以80*80*256的特征图为例，这个特征图可以理解为有80*80个像素点，每个像素点上有256个信息。这256个信息均为这个像素点的感受野内，高度浓缩的特征信息。**80*80的特征图感受野相对较少，所以浓缩的特征信息也就少。而20*20的特征图感受野大，那么其需要浓缩的信息也就多。**越小尺寸的特征图，通道数越大，这样的设计才够合理。**

   三张特征图其实就是三个网格。第一个网格为80*80，第二个网格为40*40，第三个网格为20*20，通过1*1卷积，三张特征图的大小被改为80*80*3x(5+80)，40*40*3x(5+80)，20*20*3x(5+80)。3代表了每个网格中蕴含3个anchor，（5+80）代表每个anchor包含的信息。其中5表示4个位置坐标（x，y，w，h）和一个置信度，置信度表示这个网格中可能存在物体的概率，这里的80取自coco数据集有80个类别。具体通道的表示如下图所示。

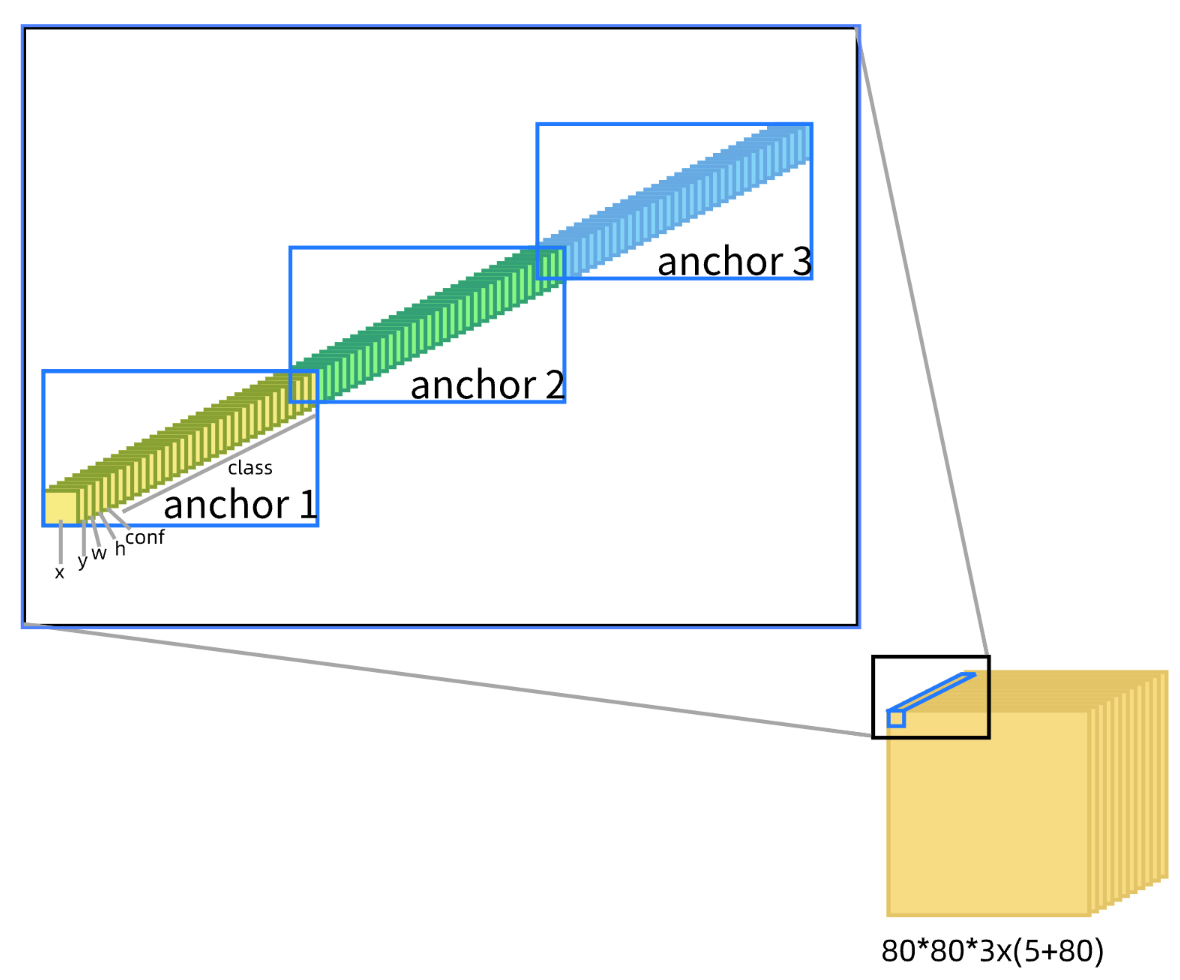
这里的11卷积将三个特征图的通道数生成为指定的通道数。每个通道数上的信息均为anchor中对应的信息。例如，特征图第一个像素的第一个通道，表示第一个网格中第一个anchor的第一个坐标x；特征图第一个像素的第86个通道，表示第一个网格中第二个anchor的第一个坐标x。11卷积网络经过训练，每个卷积核用于输出一个特定的信息，具体来说，卷积核的每个通道，赋予特征图每个高度浓缩的特征信息（也就是通道数）一个权值。这个些权值会使每个高度浓缩的特征信息相加等于一个特定的值。例如，8080的特征图有256个通道，11卷积的第一个卷积核就会负责输出第一个anchor的x，第二个卷积核则会负责输出第一个anchor的y。因为两个卷积核存在不同的权值，可以把相同的输入做不同的输出。

   以80*80的网格为例，head将特征图降维或升维至相应的格式后，再经过一个reshape，把（batch，80，80，3*（5+80））的特征图修改为（batch，3，80，80，85），方面后面的操作。若在预测阶段，再经过消除gird敏感度，并再次改变形状为（batch, 3*80*80, 85）就可以作为网络输出了;若在训练阶段，则暂不消除gird敏感度，直接输出（batch，3，80，80，85），进行损失的计算。关于消除gird敏感度后文还会提到。

YOLOv5算法原理

  在梳理完YOLO的网络结构后，此时就可以对YOLO算法的原理进行更深的研究。

   YOLO是在网格的基础上预测物体的，其中网格内anchor的置信度起了至关重要的作用。若置信度大于一定的阈值（源码默认0.25），那么就判定网格内存在物体。道理简单，但很容易让人误解。我在刚接触YOLO时是这样理解的：网络会将每个网格内包含的图形，看作一个类似二分类问题，若网格在标注框内，其标签值就为1，反之则为0。这样一来，网络就会对哪个网格内可能存在物体，哪个网格内不存在物体有了一个抽象的概念。这样就可以在预测时输出每个anchor中置信度的概率。不过好在整个图像置信度损失的计算是并行的，而不是用for循环挨个遍历网格，这样在计算置信度损失时，也会参考到周围的其他网格。

** 但是现在看来，这样的理解是错误的。**

** 损失是并行的而不是用for循环遍历网格，这一点是正确的。但我们不应该在历代YOLO算法所谓网格的概念基础上，理解网络对置信度的判断，而是应该从感受野的角度去理解**。

   YOLO的置信度可以说是比较关键的问题，置信度对YOLO的评判指标——mAP具有几乎决定性的作用。因为置信度低于阈值的框会被过滤掉，若某个目标识别出来的置信低于阈值，那么这个框就会被过滤；若某个背景的置信度较高，那么它也会被错误的识别为目标。置信度的预测是YOLO算法的重要环节，相比置信度来说，宽高坐标以及类别出现的问题会比较少。

以感受野理解网格

   先来看YOLO中的网格，下面三张图就是将三个尺度的网格绘制在原图上的情况以及预测结果。可以看出，当预测公交车这样的大物体时，即使是在最大的20*20的网格中，仅凭网格内的信息好像也显得苍白无力，即使参考了周围的网格似乎也难以预测出这么大的物体。

   根据前面网络结构的梳理，所谓的网格大小其实就是网络输出特征图的大小。例如neck的第一个检测特征层，产生了一个80*80*256的特征图，在head中被转换为80*80*3x(5+80)的大小。这个80*80其实就是网格的大小。

** 在网格的概念上，640640的原图分割成8080的网格，其中每个网格的宽高是原来的1/8，那么网格中感受到的其实就是88区域的像素。*

** 而在感受野的概念上，640640的原图被卷积为8080的特征图，特征图相对于原图做了8倍的下采样，特征图上的每个像素感受到的原图的范围要比原图多得多。**

   接下来用一维卷积来做一个简单的验证。原图的长度为16，对其做kernel=3，stride=2，padding=1的卷积，这个卷积也就是Conv模块在backbone中对图像做下采样的卷积，每次都能将特征图的尺寸缩减一半。

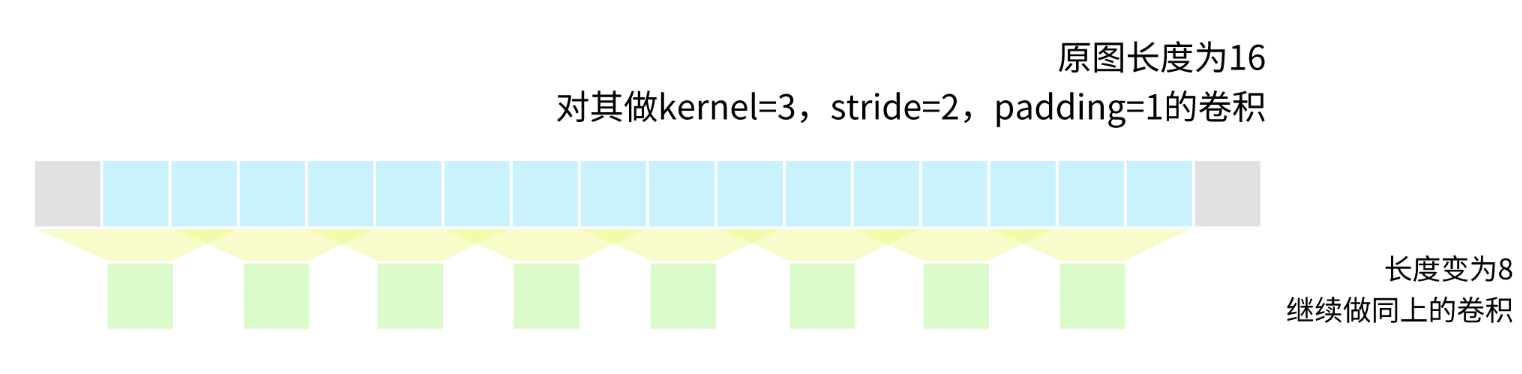
   得到了一条长度为8的特征，接下来继续做同上的卷积。

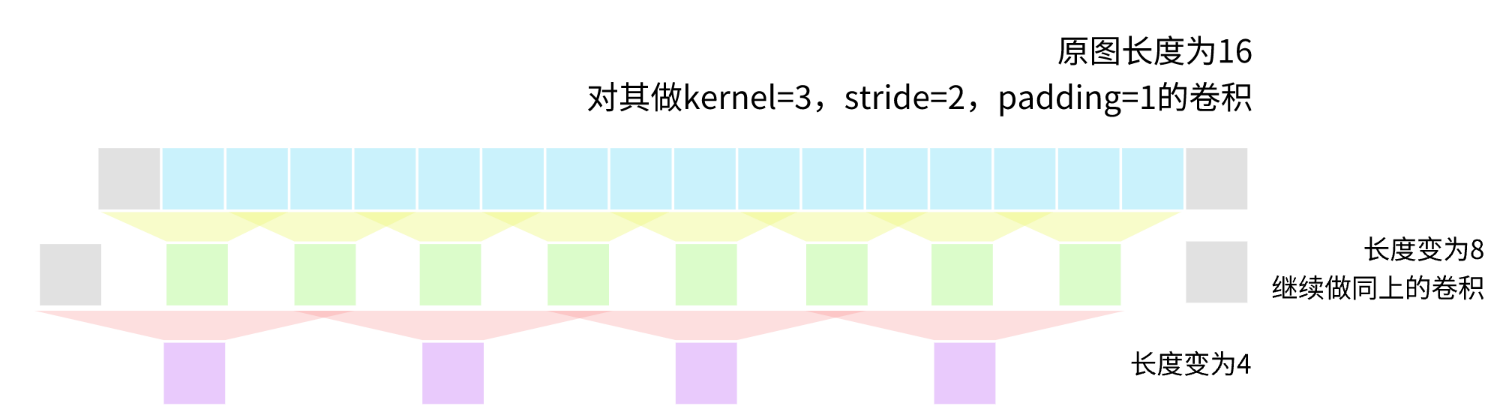
   此时得到了一条长度为4的特征。

   如果将最后的4个数看作是网格，那么它每个数在原来的向量上只能感受到4个数。

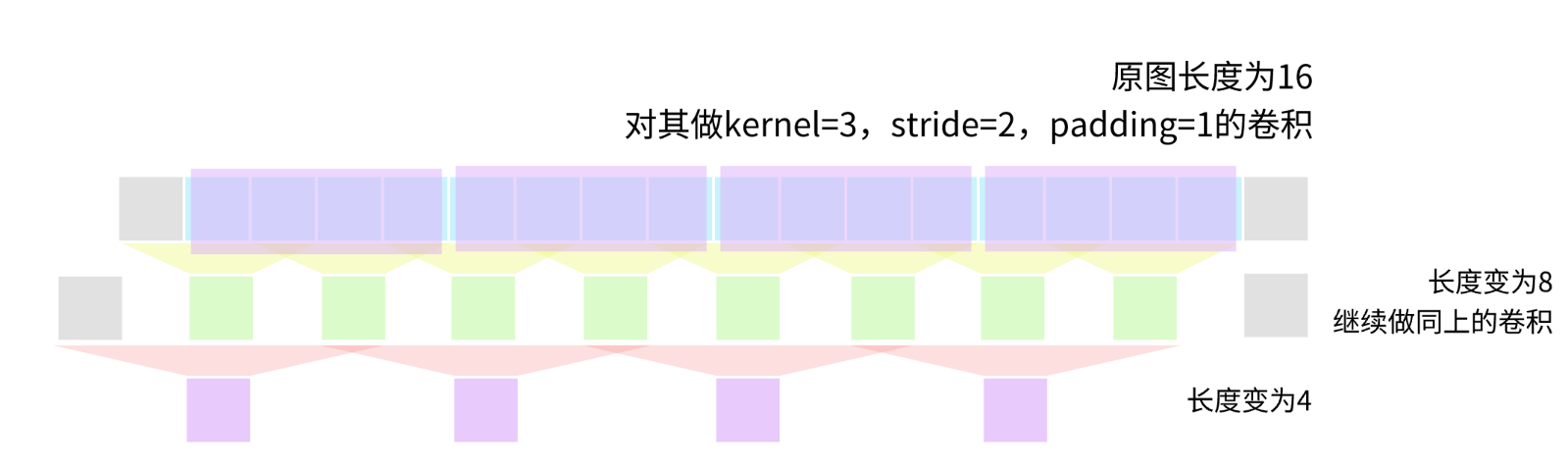
   如果将最后的4个数用感受野去理解，那么它每个数在原图的基础上可以感受到8个数。

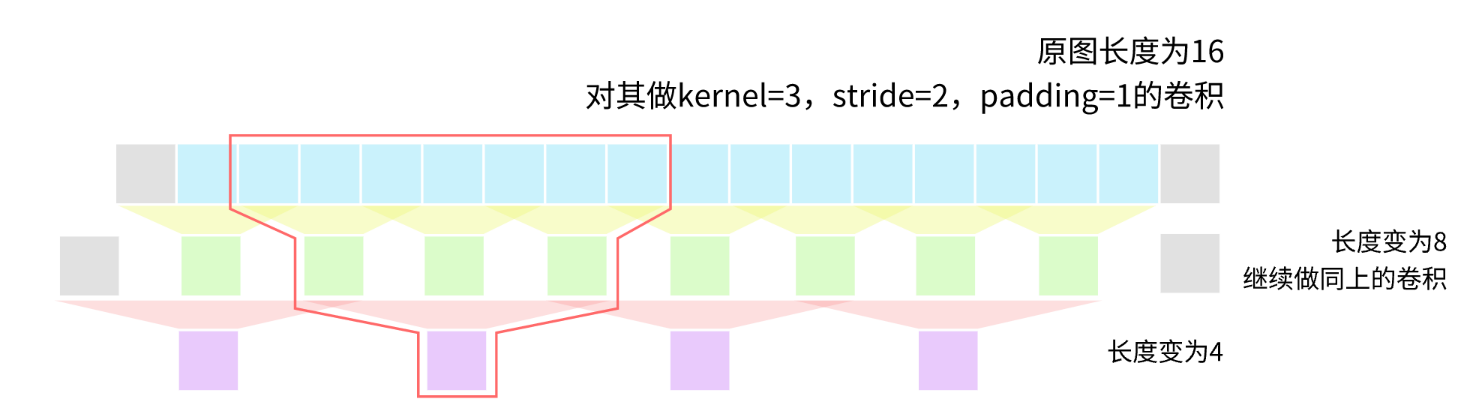
   这是在一维层面上的理解，扩展到二维层面同样实用。

   根据感受野的计算公式，当stride一直为2时，感受野的变化几乎是呈指数型上升的。

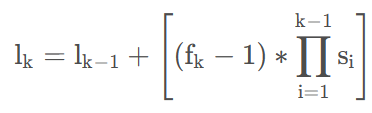
   因此感受野在下采样到达一定的倍数时，是要远大于它作为网格时感受到的信息的。那么YOLO的置信度也就好解释了。

** YOLO中所谓**网格内所感受到的信息，不仅仅是网格内部所包含的像素范围，而是一个很大的范围，下采样倍数越大，感受的范围也就更大。因此YOLO中，每个网格所感受到的范围都比网格大许多，这也解释了目标在横跨两个网格边界时，仍能很好检测的原因。再加上损失计算是并行的，而不是依次遍历每个网格，因而各个网格之间通过训练，均可以互相搭配，减小损失。

框回归以及分类

   YOLO在预测阶段预测置信度的同时，会将预测框的宽高与类别信息一并预测出，虽然网络对目标的形状大小已经有了一定的抽象概念，但在并行预测的情况下仍无法确定预测框中心的确切的位置，简单来说，对于某一个大小形状的特征，某个区域内的不同的网格都会认为它的中点应该在自己内部。这就造成同一目标可能会被多个网格预测。经过非极大值抑制便可消除置信度低与重合度较高的框。

   框回归以及分类在YOLO中存在的问题较少，也比较好理解，这里不做重点。

YOLOv5细节

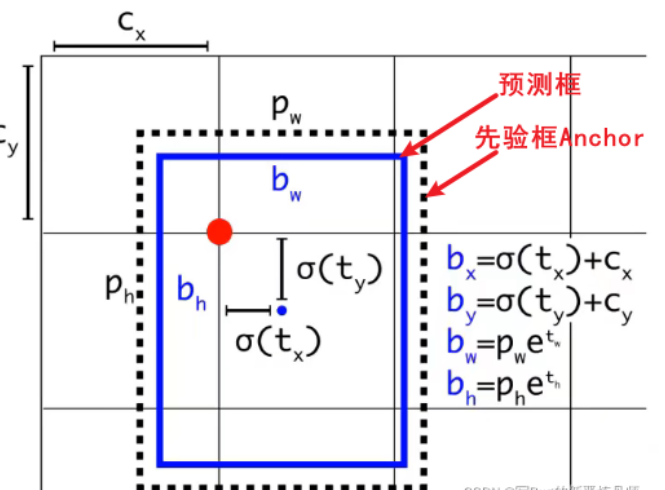
消除网格敏感度

   在YOLO v3/v4中，算法就做了消除网格敏感度的操作，是对预测出的x值以及y值经过sigmoid()函数的处理，这还是比较好理解的。因为网络预测的x值以及y值都是在anchor中的，而anchor又在网格内，anchor中的x值以及y值都是相对于所在网格坐上角的偏移量。经过sigmoid的处理，xy被限制在0-1之间，若不经过sigmoid处理，网络的对于xy的预测也是在0-1之间的，因为标签值是在0-1之间的，但不保证预测值不会超出范围，**经过了sigmoid函数的处理，输出一定被限制在0-1之间的，而且预测值有了更大的活动范围，有利于更准确的预测。**

   对于宽高的预测，网络输出将会经过一个指数函数，这样做也是为让预测值有更大的活动范围。预测值小于0时anchor缩小，大于0时anchor扩大。但其对anchor的上限没有进行限制，可能会造成anchor的无限增长。

注：消除网格敏感度是在网络计算损失之前进行。

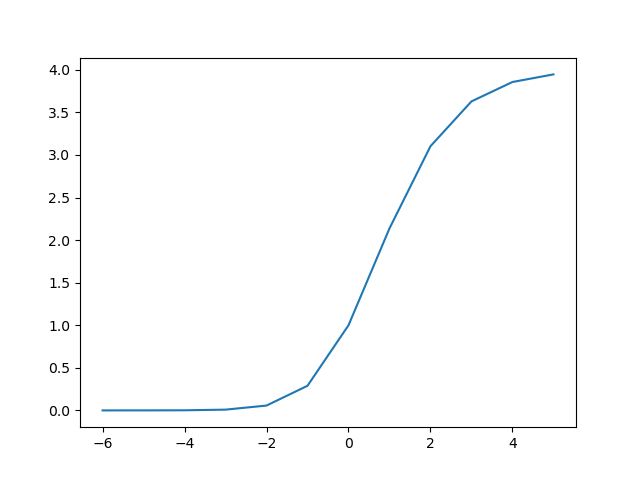
   在YOLOv5 中，对预测出的x值以及y值经过了sigmoid()*2-0.5函数的处理。下面是函数图像。它其实是将坐标点限制在了-0.5与1.5之间。这么做有两个好处。第一，若预测框的中点恰好在边框上，前面的sigmoid函数就比较难实现，因为神经网络很难预测出无穷大或无穷小；第二点是有利于增加正样本的数量，这一点后面再提。

   对于宽高的预测,YOLOv5经过了(sigmoid()*2)**2函数的处理。下面是函数图像。首先可以看到函数的值域在0-4之间，也就是说anchor的最大扩大倍数被限制为了四倍。避免anchor野蛮生长的现象。

b. 正样本匹配

   在计算损失时，正样本与负样本数量不均衡往往会使训练的效果不理想。YOLO算法中，不负责预测物体的anchor均被视为负样本，负责预测物体的anchor被视为正样本，这就造成负样本数量非常多，正样本的数量非常少。

   YOLOv5采取了一系列的方法增加正样本的数量。

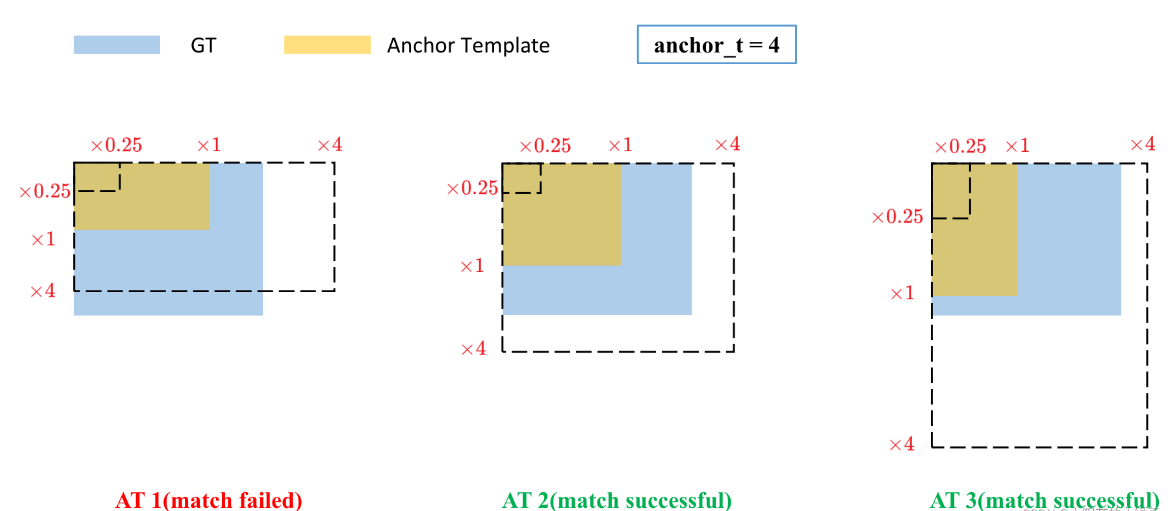
   1. 在YOLOv3/v4中，正样本的匹配是通过计算IOU进行的，去与标注框IOU最大的anchor作为正样本。而YOLO v5是通过计算标注框宽高与anchor宽高的极值判断的，只要这个极值在1/4至4之间，就表示这个anchor可以生长为这个标注框，此时便将这个anchor设为正样本。这就实现了一个标注框为其分配多个anchor作为正样本，增加了正样本的数量。

   2.前面消除网格敏感度时提到，预测框中点的偏移量被限制在了-0.5至1.5之间。其作用可以增加正样本的数量。因为把偏移量限制在-0.5-1.5之间时，相当于在网格的上下左右均探出了0.5的长度，**因为偏移量增加了0.5，所以其他网格的anchor也可以回归到标注框的位置。**既然其他框的anchor可以回归至标注框的位置，那么也可以将其中的anchor设为正样本。这个过程叫做网格的偏移。网格的偏移也极大程度的加大了正样本的数量。

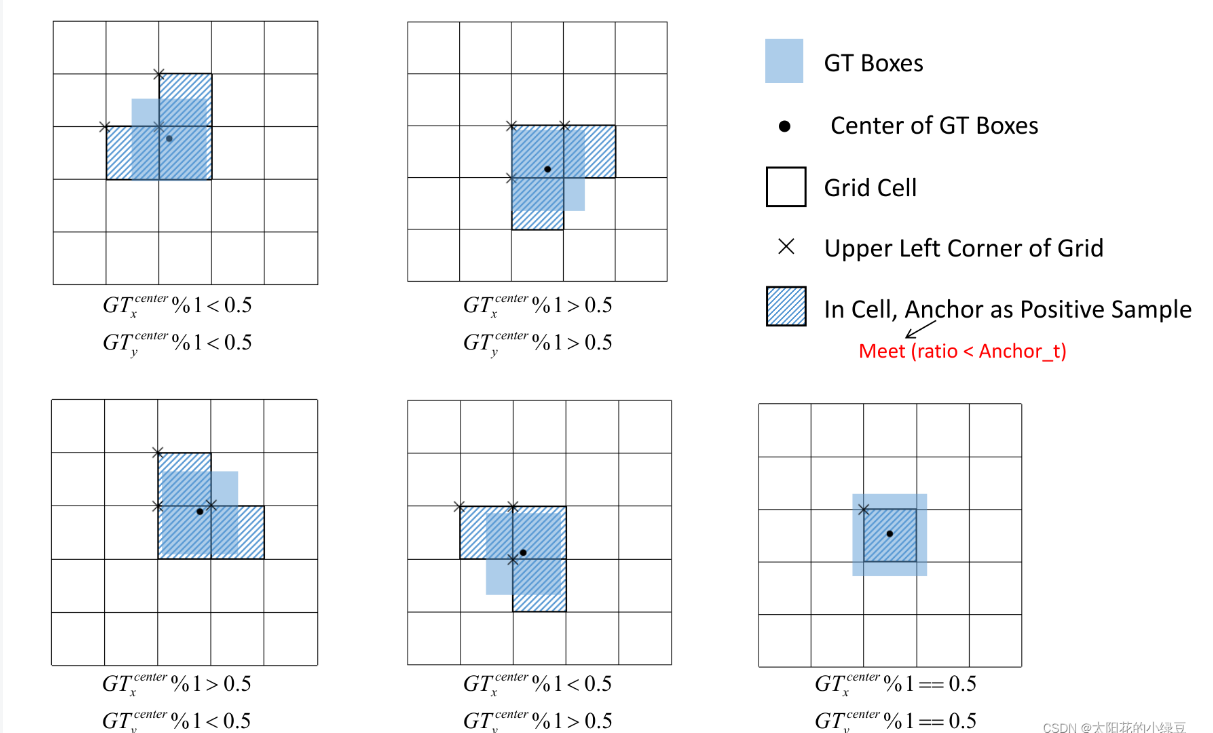
   YOLOv5先通过在本网格中分别比较3个anchor与标注框的比值，将满足条件的anchor都设为正样本，接下来又通过网格的偏移进一步增加了正样本的数量，使得正负样本不均衡的问题有了一定的改善。**增加正样本的过程其实就是增加了标签，可以理解为对同一目标又生成了许多标注框。但这样又会出现一个现象：对同一目标的标注框多了，那么对这个标注框产生的预测结果也会增多。而相比没有增加正样本时，输出的标签差别却不会太大。**这是因为上面提到过的，网络本身就会对同一目标产生多个预测框。再经过非极大值抑制，这些重复的标签就都会被过滤掉。

c. 损失计算

YOLOv5在损失计算时也有几个小细节。

    YOLOv5在类别的损失函数中，使用的是二元交叉熵损失函数，而不是softmax损失函数。因为softmax损失函数对于每个类别的处理是互斥的。而yolo考虑到了类别不互斥的情况，例如，一个类别可以是车，但也可以是汽车或货车，如果用softmax，是车就不可以是汽车，但二元交叉熵既可以是车也可以是汽车。

    YOLOv5在计算每个特征层的损失时，为每个特征层的损失增加了不同的权重。小、中、大三个不同的特征层权重分别为 4.0，1.0，0.4。检测小目标的特征层权重比较大，这是因为小目标更难预测，所以将其损失提高。特征层的权重对于不同的数据集可能存在不同的值，可以根据需求进行调整。

    YOLOv5在计算预测框损失时，并不是取的x,y,w,h与标签值之间的平方差作为损失。而是计算预测框与标注框之间的1-CIoU作为损失，CIoU越大损失越小。

    YOLOv5在计算置信度损失时，置信度的标签值取的时其所在anchor的CIoU。CIoU越大，表示这个框内存在物体的概率越大。