近端策略优化(PPO)算法是OpenAI在2017提出的一种强化学习算法,被认为是目前强化学习领域的SOTA方法,也是适用性最广的算法之一。本文将从PPO算法的基础入手,理解从传统策略梯度算法(例如REIFORCE算法)、自然策略梯度算法、信赖域策略优化算法(TRPO)直到PPO算法的演进过程,以及算法迭代过程中的优化细节。整体框图如下图所示。

图1. 本文整体框图
1. 传统策略梯度算法
1.1 从价值近似到策略近似
强化学习算法可以分为两大类:基于值函数的强化学习和基于策略的强化学习。
基于值函数的强化学习通过递归地求解贝尔曼方程来维护Q值函数(可以是离散的列表,也可以是神经网络),每次选择动作时会选择该状态下对应Q值最大的动作,使得未来积累的期望奖励值最大。经典的基于值函数的强化学习算法有Q-Learning、SARSA、DQN算法等。这些算法在学习后的Q值函数不再发生变化,每次做出的策略也是一定的,可以理解为确定性策略。基于策略的强化学习不再通过价值函数来确定选择动作的策略,而是直接学习策略本身,通过一组参数
θ
\theta
θ对策略进行参数化,并通过神经网络方法优化
θ
\theta
θ。
基于策略的强化学习用参数化概率分布
π
θ
(
a
∣
s
)
=
P
(
a
∣
s
;
θ
)
\pi_\theta(a|s)=P(a|s;\theta)
πθ(a∣s)=P(a∣s;θ)代替了基于值函数的强化学习中的确定性策略
π
:
s
→
a
\pi:s \to a
π:s→a,在返回的动作概率列表中对不同的动作进行抽样选择。
1.2 定义目标函数
基于参数化策略的思想,我们的目标就是找到那些可能获得更多奖励的动作,使它们对应的概率更大,从而策略就更有可能选择这些动作。为此,我们定义的最大化目标函数
J
(
θ
)
J(\theta)
J(θ)如下:
max
θ
J
(
θ
)
=
max
θ
E
τ
∼
π
θ
R
(
τ
)
=
max
θ
∑
τ
P
(
τ
;
θ
)
R
(
τ
)
\max_\theta J(\theta)=\max_\theta E_{\tau \sim \pi_{\theta}} R(\tau)=\max_\theta \sum_{\tau} P(\tau ; \theta) R(\tau)
θmaxJ(θ)=θmaxEτ∼πθR(τ)=θmaxτ∑P(τ;θ)R(τ)其中
τ
\tau
τ是agent与环境交互产生的状态-动作轨迹
τ
=
(
s
1
,
a
1
,
…
,
s
T
,
a
T
)
\tau=(s_1,a_1,\dots,s_T,a_T)
τ=(s1,a1,…,sT,aT),对
τ
\tau
τ求和代表的是与环境交互可能产生的所有情况。我们的目标是通过调整
θ
\theta
θ,使得获得更大奖励的轨迹出现的概率更高。
其中,轨迹
τ
\tau
τ在策略
π
θ
(
a
∣
s
)
\pi_\theta(a|s)
πθ(a∣s)下发生的概率定义为:
P
(
τ
;
θ
)
=
[
∏
t
=
0
T
P
(
s
t
+
1
∣
s
t
,
a
t
)
⋅
π
θ
(
a
t
∣
s
t
)
]
P(\tau ; \theta)=\left[\prod_{t=0}^{T} P\left(s_{t+1} \mid s_{t}, a_{t}\right) \cdot \pi_{\theta}\left(a_{t} \mid s_{t}\right)\right]
P(τ;θ)=[t=0∏TP(st+1∣st,at)⋅πθ(at∣st)]表示为状态转移概率和动作选择概率的乘积,因为状态和动作决定轨迹。
1.3 导出策略梯度
与神经网络的优化思路相同,为了通过参数
θ
\theta
θ优化目标函数,我们需要计算目标函数
J
(
θ
)
J(\theta)
J(θ)对
θ
\theta
θ的导数:
∇
θ
J
(
θ
)
=
∑
τ
∇
θ
P
(
τ
;
θ
)
R
(
τ
)
=
∑
τ
P
(
τ
;
θ
)
∇
θ
P
(
τ
;
θ
)
P
(
τ
;
θ
)
R
(
τ
)
=
∑
τ
P
(
τ
;
θ
)
∇
θ
log
P
(
τ
;
θ
)
R
(
τ
)
=
E
τ
∼
π
θ
∇
θ
log
P
(
τ
;
θ
)
R
(
τ
)
\begin{aligned}\nabla_{\theta} J(\theta)&=\sum_{\tau} \nabla_{\theta} P(\tau ; \theta) R(\tau)\\&=\sum_{\tau} P(\tau ; \theta) \frac{\nabla_{\theta} P(\tau ; \theta)}{P(\tau ; \theta)} R(\tau)\\&=\sum_\tau P(\tau;\theta)\nabla_\theta\log P(\tau;\theta)R(\tau)\\&=\mathbb{E}_{\tau\sim\pi_{\theta}}\nabla_{\theta}\log P(\tau;\theta)R(\tau)\end{aligned}
∇θJ(θ)=τ∑∇θP(τ;θ)R(τ)=τ∑P(τ;θ)P(τ;θ)∇θP(τ;θ)R(τ)=τ∑P(τ;θ)∇θlogP(τ;θ)R(τ)=Eτ∼πθ∇θlogP(τ;θ)R(τ)推导过程中使用了对数导数技巧,将
P
(
τ
;
θ
)
P(\tau ; \theta)
P(τ;θ)表示为对数的形式,从而可以方便的重写为:
∇
θ
log
P
(
τ
;
θ
)
=
∇
θ
[
∑
t
=
0
T
log
P
(
s
t
+
1
∣
s
t
,
a
t
)
+
∑
t
=
0
T
log
π
θ
(
a
t
∣
s
t
)
]
=
∑
t
=
0
T
∇
θ
log
π
θ
(
a
t
∣
s
t
)
\begin{aligned}\nabla_{\theta} \log P(\tau ; \theta)&=\nabla_{\theta}\left[\sum_{t=0}^{T} \log P\left(s_{t+1} \mid s_{t}, a_{t}\right)+\sum_{t=0}^{T} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right)\right]\\&=\sum_{t=0}^{T} \nabla_{\theta}\log \pi_{\theta}(a_{t} \mid s_{t})\end{aligned}
∇θlogP(τ;θ)=∇θ[t=0∑TlogP(st+1∣st,at)+t=0∑Tlogπθ(at∣st)]=t=0∑T∇θlogπθ(at∣st)其中第一步中第一项的状态转移概率只与环境有关,而与
θ
\theta
θ无关。
然而,到目前为止的计算还需要对所有可能的轨迹进行求和,这在实际的RL问题中是难以处理的,我们需要利用轨迹样本进行梯度近似,表达式如下:
∇
θ
J
(
θ
)
≈
1
m
∑
i
=
1
m
∇
θ
log
P
(
τ
(
i
)
;
θ
)
R
(
τ
(
i
)
)
=
1
m
∑
i
=
1
m
(
∑
t
(
i
)
=
0
T
(
i
)
∇
θ
log
π
θ
(
a
t
(
i
)
∣
s
t
(
i
)
)
)
R
(
τ
(
i
)
)
≈
1
n
∑
i
=
1
n
(
∇
θ
log
π
θ
(
a
t
(
i
)
∣
s
t
(
i
)
)
)
R
(
t
(
i
)
)
\begin{aligned}\nabla_{\theta}J(\theta)&\approx\frac{1}{m}\sum_{i=1}^{m}\nabla_{\theta}\log P(\tau^{(i)};\theta)R(\tau^{(i)})\\&=\frac{1}{m}\sum_{i=1}^{m}(\sum_{t^{(i)}=0}^{T^{(i)}} \nabla_{\theta}\log \pi_{\theta}(a_{t^{(i)}} \mid s_{t^{(i)}}))R(\tau^{(i)})\\&\approx\frac{1}{n}\sum_{i=1}^{n}( \nabla_{\theta}\log \pi_{\theta}(a_{t^{(i)}} \mid s_{t^{(i)}}))R(t^{(i)})\end{aligned}
∇θJ(θ)≈m1i=1∑m∇θlogP(τ(i);θ)R(τ(i))=m1i=1∑m(t(i)=0∑T(i)∇θlogπθ(at(i)∣st(i)))R(τ(i))≈n1i=1∑n(∇θlogπθ(at(i)∣st(i)))R(t(i))现在的表达式是完全可计算的,现在只需要给出策略
π
θ
\pi_\theta
πθ的明确定义,就可以计算得到
∇
θ
J
(
θ
)
\nabla_{\theta}J(\theta)
∇θJ(θ),从而用策略梯度更新规则:
θ
←
θ
+
α
∇
θ
J
(
θ
)
\begin{aligned}\theta\leftarrow\theta+\alpha\text{}\nabla_\theta J(\theta)\end{aligned}
θ←θ+α∇θJ(θ)来对
θ
\theta
θ进行调整优化,从而不断迭代至最优策略。
这里给出两种常见的策略示例及其对应梯度。
- Softmax策略 对于离散动作空间,多使用Softmax策略。其定义如下: π θ ( s , a ) = e ϕ ( s , a ) ⊤ θ ∑ a ′ ∈ A e ϕ ( s , a ′ ) ⊤ θ \pi_{\theta}(s,a)=\frac{e^{\phi(s,a)^\top\theta}}{\sum_{a'\in A}e^{\phi(s,a')^\top}\theta} πθ(s,a)=∑a′∈Aeϕ(s,a′)⊤θeϕ(s,a)⊤θ对应的策略梯度为: ∇ θ log π θ ( a ∣ s ) = ϕ ( s , a ) − ∑ a ′ ∈ A ϕ ( s , a ′ ) π θ ( a ∣ s ) \nabla_\theta\log\pi_\theta(a\mid s)=\phi(s,a)-\sum\limits_{a'\in A}\phi(s,a')\pi_\theta(a\mid s) ∇θlogπθ(a∣s)=ϕ(s,a)−a′∈A∑ϕ(s,a′)πθ(a∣s)梯度的结果可以解释为观察到的特征向量减去所有动作的平均特征向量。因此,如果奖励信号很高并且观察到的向量与平均向量相差很大,就会有增加该动作概率的强烈趋势。
- 高斯策略 对于连续动作空间,多使用高斯策略。其定义如下: π θ ( a ∣ s ) = 1 2 π σ θ e − a − μ θ 2 σ θ 2 \quad\pi_{\theta}(a\mid s)=\dfrac{1}{\sqrt{2\pi}\sigma_{\theta}}e^{-\frac{a-\mu_{\theta}}{2\sigma_{\theta}^{2}}} πθ(a∣s)=2πσθ1e−2σθ2a−μθ其中正态分布的均值 μ θ = ϕ ( s , a ) ⊤ θ \mu_\theta=\phi(s,\mathrm{a})^\top\theta μθ=ϕ(s,a)⊤θ。 对应的策略梯度为: ∇ θ log ( π θ ( a ∣ s ) ) = ( a − μ θ ) ϕ ( s ) σ θ 2 \nabla_\theta\log(\pi_\theta(a\mid s))=\dfrac{(a-\mu_\theta)\phi(s)}{\sigma_\theta^2} ∇θlog(πθ(a∣s))=σθ2(a−μθ)ϕ(s) 同样地,在高回报的情况下,远离均值的动作会触发强烈的更新信号。由于概率总和必须为 1,因此增加某些轨迹的概率也意味着减少其他轨迹的概率。
在实际任务中,我们没有必要手动计算偏导数,使用深度学习框架的自动求导就好了。为了实现自动求导,我们只需要根据之前策略梯度的推导结果,定义损失函数如下:
L
(
a
,
s
,
r
)
=
−
log
(
π
θ
(
a
∣
s
)
)
r
\begin{aligned}\mathcal{L}(a,s,r)=-\log\left(\pi_\theta(a\mid s)\right)r\end{aligned}
L(a,s,r)=−log(πθ(a∣s))r就可以让计算机解决所有的推导。
1.4 算法实现
Williams提出的REINFORCE算法是经典的策略梯度算法之一。其伪代码如下所示:

图2. REINFORCE算法
算法思路简介明了,是最简单的基于似然比的策略梯度强化学习算法。接下来我们将介绍如何对REINFORCE算法进行一步步的优化,直到发展为强大的PPO算法的过程。
2. 自然策略梯度算法
自然策略梯度算法揭露了传统策略梯度算法的缺点以及补救的方法,尽管自然梯度已被TRPO和PPO等算法超越,但掌握它的基本原理对于理解这些当代RL算法至关重要。
对自然梯度的完整讨论需要具备较强的数学功底,需要许多冗长的推导。我们的讨论将主要关注推理和直觉,为更深入的推导提供外部参考。
2.1 传统策略梯度算法的缺陷
在传统的策略梯度算法中,我们根据目标函数梯度
∇
θ
J
(
θ
)
\nabla_\theta J(\theta)
∇θJ(θ)和步长
α
\alpha
α更新策略权重
θ
\theta
θ,这样的更新过程可能会出现两个常见的问题:
- 过冲(Overshooting):更新错过了奖励峰值并落入了次优策略区域
- 下冲(Undershooting):在梯度方向上采取过小的更新步长会导致收敛缓慢
在监督学习问题中,overshooting并不是什么大问题,因为数据是固定的,我们可以在下一个epoch中重新纠正,但在强化学习问题中,如果因为overshooting陷入了一个较差的策略区域,则未来的样本批次可能不会提供太多有意义的信息,用较差的数据样本再去更新策略,从而陷入了糟糕的正反馈中无法恢复。较小的学习率可能会解决这个问题,但会导致收敛速度变慢的undershooting问题。

图3. overshooting示例:如果在梯度方向上采取的步骤太大(左),更新可能会错过奖励峰值并落在具有低梯度的次优区域(右),需要多次迭代才能逃逸或者甚至无法逃逸
为了避免overshooting带来的严重后果,一种直觉方法是限制每次更新步长的上限:
Δ
θ
∗
=
arg max
∣
∣
Δ
θ
∣
∣
≤
ϵ
J
(
θ
+
Δ
θ
)
\Delta\theta^*=\argmax_{||\Delta\theta||\leq\epsilon}J(\theta+\Delta\theta)
Δθ∗=∣∣Δθ∣∣≤ϵargmaxJ(θ+Δθ)其中
∣
∣
Δ
θ
∣
∣
||\Delta\theta||
∣∣Δθ∣∣代表更新前后策略权重的欧式距离。
尽管听起来很合理,但实际效果并不是像我们预期的那样,原因是不同的分布对参数变化的敏感度是不同的。比如在下图中,我们都让策略权重变化了1个单位的欧式距离,但是对左图的影响是远大于右图的。所以,只限制参数是不合理的,更应该考虑分布对参数变化的敏感度,传统的策略梯度算法无法考虑到这种曲率变化,我们需要引入二阶导数,这正是自然策略梯度相较于传统策略梯度算法的区别。
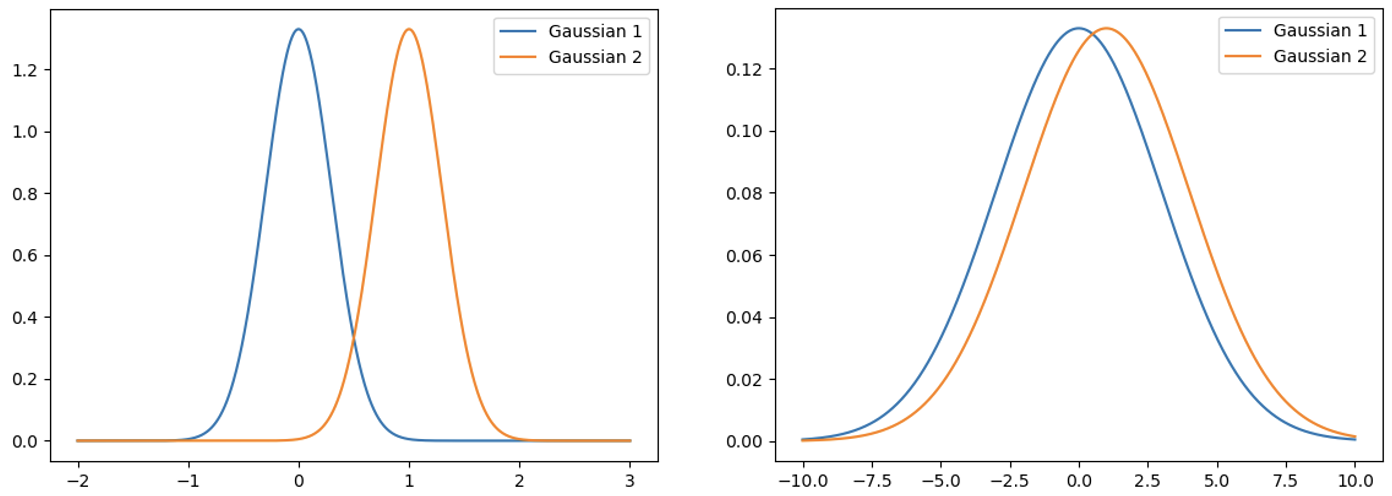
图4. 高斯函数示例:两组高斯函数中的均值分别为0和1,左图的高斯函数标准差为0.3,右图为3
2.2 限制策略更新的差异
我们需要表示策略(分布)之间的差异,而不是参数本身的差异。计算两个概率分布之间的差异,最常见的是KL散度,也称为相对熵,描述了两个概率分布之间的距离:
D
K
L
(
π
θ
∥
π
θ
+
Δ
θ
)
=
∑
x
∈
X
π
θ
(
x
)
log
(
π
θ
(
x
)
π
θ
+
Δ
θ
(
x
)
)
\mathcal{D}_{\mathrm{KL}}(\pi_{\theta}\parallel\pi_{\theta+\Delta\theta})=\sum_{x\in\mathcal{X}}\pi_{\theta}(x)\log\left(\frac{\pi_{\theta}{}(x)}{\pi_{\theta+}\Delta\theta(x)}\right)
DKL(πθ∥πθ+Δθ)=x∈X∑πθ(x)log(πθ+Δθ(x)πθ(x))调整后的策略更新限制为:
Δ
θ
∗
=
arg max
D
K
L
(
π
θ
∥
π
θ
+
Δ
θ
)
≤
ϵ
J
(
θ
+
Δ
θ
)
\Delta\theta^*=\argmax_{\mathcal{D}_{\mathrm{KL}}(\pi_{\theta}\parallel\pi_{\theta+\Delta\theta})\leq\epsilon}J(\theta+\Delta\theta)
Δθ∗=DKL(πθ∥πθ+Δθ)≤ϵargmaxJ(θ+Δθ)通过计算这个表达式,我们可以确保在参数空间中执行大更新的同时,保证策略本身的改变不超过阈值。然而,计算KL散度需要遍历所有的状态-动作对,因此我们需要一些化简来处理现实的RL问题。
接下来的数学部分,可以在Katerina Fragkiadaki(CMU)关于自然策略梯度的PPT中找到详细的证明推导。
首先,我们使用拉格朗日松弛将原表达式的发散约束转化为惩罚项,得到一个更容易求解的表达式:
Δ
θ
∗
=
arg
max
Δ
θ
J
(
θ
+
Δ
θ
)
−
λ
(
D
K
L
(
π
θ
∥
π
θ
+
Δ
θ
)
−
ϵ
)
\Delta\theta^{*}=\operatorname*{arg}\operatorname*{max}_{\Delta\theta}J(\theta+\Delta\theta)-\lambda({\mathcal{D}}_{\mathrm{KL}}(\pi_{\theta}\parallel\pi_{\theta{+}\Delta\theta})-\epsilon)
Δθ∗=argΔθmaxJ(θ+Δθ)−λ(DKL(πθ∥πθ+Δθ)−ϵ)由于计算KL散度需要遍历所有的状态-动作对,我们必须用近似方法来化简。通过泰勒展开:
Δ
θ
∗
≈
arg max
Δ
θ
J
(
θ
old
)
+
∇
θ
J
(
θ
)
∣
θ
=
θ
old
⋅
Δ
θ
−
1
2
λ
(
Δ
θ
⊤
∇
θ
2
D
KL
(
π
θ
old
∥
π
θ
)
∣
θ
=
θ
old
Δ
θ
)
+
λ
ϵ
\Delta\theta^*\approx\argmax_{\Delta\theta}J(\theta_{\text{old}})+\nabla_\theta J(\theta)|_{\theta=\theta_{\text{old}}}\cdot\Delta\theta-\dfrac{1}{2}\lambda\left(\Delta\theta^{\top}\nabla_\theta^2\mathcal{D}_{\text{KL}}(\pi_{\theta_{\text{old}}}\parallel\pi_\theta)|_{\theta={}\theta_{\text{old}}}\Delta\theta\right)+\lambda\epsilon
Δθ∗≈ΔθargmaxJ(θold)+∇θJ(θ)∣θ=θold⋅Δθ−21λ(Δθ⊤∇θ2DKL(πθold∥πθ)∣θ=θoldΔθ)+λϵ目标函数近似于一阶泰勒展开(与散度相比,二阶展开可以忽略不计),KL散度近似于二阶泰勒展开(零阶和一阶差分的计算结果为0)。我们可以进一步化简,通过
- 用费舍尔信息矩阵(Fisher information matrix)替换二阶KL导数
- 删除所有不依赖于 Δ θ \Delta\theta Δθ的项
可以得到:
Δ
θ
∗
≈
arg max
Δ
θ
∇
θ
J
(
θ
)
∣
θ
=
θ
old
⋅
Δ
θ
−
1
2
λ
(
Δ
θ
⊤
F
(
θ
old
)
Δ
θ
)
\Delta\theta^*\approx \argmax_{\Delta\theta}\nabla_\theta J(\theta)|_{\theta=\theta_\text{old}}\cdot\Delta\theta-\frac{1}{2}\lambda(\Delta\theta^\top F(\theta_\text{old})\Delta\theta)
Δθ∗≈Δθargmax∇θJ(θ)∣θ=θold⋅Δθ−21λ(Δθ⊤F(θold)Δθ)用费舍尔信息矩阵代替二阶导数的原因,除了符号紧凑性外,还可以大大减少计算开销。原先的Hessian矩阵是一个
∣
θ
∣
⋅
∣
θ
∣
|\theta|\cdot|\theta|
∣θ∣⋅∣θ∣的矩阵,每个元素都是二阶导数,完整的计算可能非常麻烦,而对于Fisher信息矩阵,有一个替代表达式:
F
(
θ
)
=
E
θ
[
∇
θ
log
π
θ
(
x
)
∇
θ
log
π
θ
(
x
)
⊤
]
F(\theta)=\mathbb{E}_{\theta}\begin{bmatrix}\nabla_{\theta}\log\pi_{\theta}(x)\nabla_\theta\log\pi_\theta(x)^\top\end{bmatrix}
F(θ)=Eθ[∇θlogπθ(x)∇θlogπθ(x)⊤]可以表示为策略梯度的外积,在局部等效于Hessian,同时计算效率更高(因为传统策略梯度的这些值
∇
θ
log
π
θ
(
x
)
\nabla_{\theta}\log\pi_{\theta}(x)
∇θlogπθ(x)本身也是我们需要的,无需再重复计算,同时期望意味着可以使用样本近似)。
2.3 解决KL约束问题
对于近似简化后的表达式,可以通过将关于
Δ
θ
\Delta\theta
Δθ的梯度设置为0,来找到最优的权重更新
Δ
θ
\Delta\theta
Δθ:
0
=
∂
∂
Δ
θ
(
∇
θ
J
(
θ
)
Δ
θ
−
1
2
λ
Δ
θ
⊤
F
(
θ
)
Δ
θ
)
=
∇
θ
J
(
θ
)
−
1
2
λ
F
(
θ
)
Δ
θ
\begin{aligned}0&=\frac{\partial}{\partial\Delta\theta}\left(\nabla_{\theta}J(\theta)\Delta\theta-\frac{1}{2}\lambda\Delta\theta^{\top}F(\theta)\Delta\theta\right)\\ &=\nabla_\theta J(\theta)-\frac{1}{2}\lambda F(\theta)\Delta\theta\\\end{aligned}
0=∂Δθ∂(∇θJ(θ)Δθ−21λΔθ⊤F(θ)Δθ)=∇θJ(θ)−21λF(θ)Δθ
∴
λ
F
(
θ
)
Δ
θ
=
−
2
∇
θ
J
(
θ
)
Δ
θ
=
−
2
λ
F
(
θ
)
−
1
∇
θ
J
(
θ
)
\begin{aligned}\therefore\lambda F(\theta)\Delta\theta&=-2\nabla_\theta J(\theta)\\ \Delta\theta&=-\frac{2}{\lambda}F(\theta)^{-1}\nabla_{\theta}J(\theta)\end{aligned}
∴λF(θ)ΔθΔθ=−2∇θJ(θ)=−λ2F(θ)−1∇θJ(θ)其中,
λ
\lambda
λ是一个常数,可以吸收到学习率
α
\alpha
α中。根据
D
K
L
(
π
θ
∥
π
θ
+
Δ
θ
)
≤
ϵ
\mathcal{D}_{\mathrm{KL}}(\pi_{\theta}\parallel\pi_{\theta+\Delta\theta}) \leq \epsilon
DKL(πθ∥πθ+Δθ)≤ϵ,我们可以推出动态学习率:
α
=
2
ϵ
∇
J
(
θ
)
⊤
F
(
θ
)
−
1
∇
J
(
θ
)
\alpha=\sqrt{\dfrac{2\epsilon}{\nabla J(\theta)^\top}F(\theta)^{-1}\nabla J(\theta)}
α=∇J(θ)⊤2ϵF(θ)−1∇J(θ)可以确保每次更新的KL散度(近似)等于
ϵ
\epsilon
ϵ。
最后,我们提取自然策略梯度,它是针对流形曲率校正的梯度:
∇
~
J
(
θ
)
=
F
(
θ
)
−
1
∇
J
(
θ
)
\tilde{\nabla}J(\theta) = F(\theta)^{-1}\nabla J(\theta)
∇~J(θ)=F(θ)−1∇J(θ)这种自然策略梯度在距离约束内给出了黎曼空间中最陡的下降方向,而不是传统上假设的欧几里德空间中的最陡下降方向。与传统的策略梯度相比,唯一的区别是与逆Fisher矩阵相乘。
最终的权重更新方案为:
Δ
θ
=
2
ϵ
∇
J
(
θ
)
⊤
F
(
θ
)
−
1
∇
J
(
θ
)
∇
~
J
(
θ
)
\Delta\theta=\sqrt{\frac{2\epsilon}{\nabla J(\theta)^\top F(\theta)^{-1}\nabla J(\theta)}} \tilde{\nabla} J(\theta)
Δθ=∇J(θ)⊤F(θ)−1∇J(θ)2ϵ∇~J(θ)该方案的强大之处在于,无论分布的表示如何,它总是以相同的幅度改变策略。
2.4 算法实现
自然策略梯度算法的完整概述伪代码如下。其中策略梯度和Fisher矩阵在实际计算时都是使用样本估计的。

图5. 自然策略梯度算法
最终结果在两个方面不同于传统的策略梯度算法:
- 考虑到策略对局部变化的敏感性,策略梯度由逆Fisher矩阵校正,而传统的梯度方法假定更新为欧几里得距离。
- 更新步长 α \alpha α具有适应梯度和局部敏感性的动态表达式,确保无论参数化如何,策略变化幅度为 ϵ \epsilon ϵ。在传统方法中, α \alpha α通常设置为一些标准值,如0.1或0.01。
3. 信赖域策略优化算法(TRPO)
Trust region policy optimization(TPRO)算法是现代强化学习的基础,它以自然策略梯度优化为基础,迅速获得普及,成为主流强化学习算法,因为它在经验上比自然策略梯度算法表现得更好、更稳定。尽管此后它已被近端策略优化 (PPO) 超越,但它的仍然具有重要的意义。
我们将讨论TRPO背后的单调改进定理(关注直觉)以及将其与自然策略梯度区分开的三个变化。
3.1 自然策略梯度算法的缺陷
- 近似值可能会违反KL约束,从而导致分析得出的步长过大,超出限制要求
- 矩阵 F − 1 F^{-1} F−1的计算时间太长,是 O ( N 3 ) O(N^3) O(N3)复杂度的运算
- 我们没有检查更新是否真的改进了策略。由于存在大量的近似过程,策略可能并没有优化
3.2 算法理论
针对自然策略梯度算法的问题,我们希望可以对策略的优化进行量化,从而保证每次的更新一定是优化作用的。为此,我们需要计算两种策略之间预期回报的差异。这里采用的是原策略预期回报添加新策略预期优势的方式。该表达式在原策略下计算优势函数,无需重新采样:
J
(
π
θ
+
Δ
θ
)
=
J
(
π
θ
)
+
E
τ
∼
π
θ
+
Δ
θ
∑
t
=
0
∞
γ
t
A
π
θ
(
s
t
,
a
t
)
J(\pi_{\theta+\Delta\theta})=J(\pi_{\theta})+\mathbb{E}_{\tau\sim\pi_{\theta+}\Delta\theta}\sum_{t=0}^{\infty}\gamma^t A^{\pi_{\theta}}(s_t,a_t)
J(πθ+Δθ)=J(πθ)+Eτ∼πθ+Δθt=0∑∞γtAπθ(st,at)其中优势函数的定义为:
A
π
θ
(
s
,
a
)
=
E
(
Q
π
θ
(
s
,
a
)
−
V
π
θ
(
s
)
)
A^{\pi_\theta}(s,a) = \mathbb{E}\left(Q^{\pi_\theta}{(s,a)-V^{\pi_\theta}}(s)\right)
Aπθ(s,a)=E(Qπθ(s,a)−Vπθ(s))在给定的策略和状态下,计算特定动作
a
a
a的期望累积奖励与总体期望值的差值,描述了该动作的相对吸引力。
由于时间范围是无限的,引入状态的折扣分布
ρ
π
(
s
)
=
(
P
(
s
0
=
s
)
+
γ
P
(
s
1
=
s
)
+
γ
2
P
(
s
2
=
s
)
+
…
)
\rho_{\pi}(s)=(P(s_0=s)+\gamma P(s_1=s)+\gamma^2P(s_2=s)+\ldots)
ρπ(s)=(P(s0=s)+γP(s1=s)+γ2P(s2=s)+…),原差异表达式可重新表示为:
J
(
π
θ
+
Δ
θ
)
=
J
(
π
θ
)
+
∑
s
∈
S
ρ
π
θ
+
Δ
θ
(
s
)
∑
a
∈
A
π
θ
+
△
θ
(
a
∣
s
)
A
π
θ
(
s
,
a
)
J(\pi_{\theta+\Delta\theta})=J(\pi_\theta)+\sum\limits_{s\in\mathcal{S}}\rho_{\pi_{\theta+}\Delta\theta}(s)\sum\limits_{a\in\mathcal{A}}\pi_{\theta+\triangle\theta}(a\mid s)A^{\pi_\theta}(s,a)
J(πθ+Δθ)=J(πθ)+s∈S∑ρπθ+Δθ(s)a∈A∑πθ+△θ(a∣s)Aπθ(s,a)我们无法在不对更新策略进行采样的情况下知道对应于更新策略的状态分布,故引入近似误差,使用**当前策略近似**:
J
(
π
θ
+
Δ
θ
)
≈
J
(
π
θ
)
+
∑
s
∈
S
ρ
π
θ
(
s
)
∑
a
∈
A
π
θ
+
△
θ
(
a
∣
s
)
A
π
θ
(
s
,
a
)
J(\pi_{\theta+\Delta\theta})\approx J(\pi_\theta)+\sum\limits_{s\in\mathcal{S}}\rho_{\pi_{\theta}}(s)\sum\limits_{a\in\mathcal{A}}\pi_{\theta+\triangle\theta}(a\mid s)A^{\pi_\theta}(s,a)
J(πθ+Δθ)≈J(πθ)+s∈S∑ρπθ(s)a∈A∑πθ+△θ(a∣s)Aπθ(s,a)接下来,我们将状态分布求和替换为期望,方便实际计算时使用蒙特卡洛模拟进行采样,同时将动作求和替换为**重要性采样**。通过重要性采样,可以有效利用当前策略的行动期望,并针对新策略下的概率进行了修正:
J
(
π
θ
+
Δ
θ
)
≈
J
(
π
θ
)
+
E
s
∼
ρ
π
θ
π
θ
+
Δ
θ
(
a
∣
s
)
π
θ
(
a
∣
s
)
A
π
θ
(
s
,
a
)
J(\pi_{\theta+\Delta\theta})\approx J(\pi_\theta)+\mathbb{E}_{s\sim\rho_{\pi\theta}}\dfrac{\pi_{\theta+\Delta\theta}(a\mid s)}{\pi_\theta(a\mid s)}A^{\pi_\theta}(s,a)
J(πθ+Δθ)≈J(πθ)+Es∼ρπθπθ(a∣s)πθ+Δθ(a∣s)Aπθ(s,a)描述更新策略相对于原策略的预期优势称为**替代优势(surrogate advantage)**:
J
(
π
θ
+
Δ
θ
)
−
J
(
π
θ
)
≈
E
s
∼
ρ
π
θ
π
θ
+
Δ
θ
(
a
∣
s
)
π
θ
(
a
∣
s
)
A
π
θ
(
s
,
a
)
=
L
π
θ
(
π
θ
+
Δ
θ
)
J(\pi_{\theta+\Delta\theta})-J(\pi_{\theta})\approx\mathbb{E}_{s\sim\rho_{\pi\theta}}\dfrac{\pi_{\theta+\Delta\theta}(a\mid s)}{\pi_{\theta}(a\mid s)}A^{\pi_{\theta}}(s,a)=\mathcal{L}_{\pi_{\theta}}(\pi_{\theta+{\Delta\theta}})
J(πθ+Δθ)−J(πθ)≈Es∼ρπθπθ(a∣s)πθ+Δθ(a∣s)Aπθ(s,a)=Lπθ(πθ+Δθ)之前产生的近似误差可以用两种策略之间最坏情况的KL散度表示:
J
(
π
θ
+
Δ
θ
)
−
J
(
π
θ
)
≥
L
π
θ
(
π
θ
+
Δ
θ
)
−
C
D
K
L
m
a
x
(
π
θ
∣
∣
π
θ
+
Δ
θ
)
J(\pi_{\theta+\Delta\theta})-J(\pi_{\theta})\geq\mathcal{L}_{\pi\theta}(\pi_{\theta+{\Delta}\theta})-C\mathcal{D}_{K L}^{\mathrm{max}}(\pi_{\theta}||\pi_{\theta+{}\Delta\theta})
J(πθ+Δθ)−J(πθ)≥Lπθ(πθ+Δθ)−CDKLmax(πθ∣∣πθ+Δθ)论文中推导出
C
C
C的值以及目标函数改进的下限。如果我们改进右侧,可以保证左侧也得到改进。本质上,如果替代优势
L
π
θ
(
π
θ
+
Δ
θ
)
\mathcal{L}_{\pi_{\theta}}(\pi_{\theta+{\Delta\theta}})
Lπθ(πθ+Δθ)超过最坏情况下的近似误差
C
D
K
L
m
a
x
(
π
θ
∣
∣
π
θ
+
Δ
θ
)
C\mathcal{D}_{K L}^{\mathrm{max}}(\pi_{\theta}||\pi_{\theta+{}\Delta\theta})
CDKLmax(πθ∣∣πθ+Δθ),我们一定会改进目标。
这就是单调改进定理。相应的过程是最小化最大化算法(MM)。即如果我们改进下限,我们也会将目标改进至少相同的量。
3.2 算法实现
在实际的算法实现方面,TRPO和自然策略梯度算法没有太大的区别。TRPO主要有三个改进,每个改进都解决了原始算法中的一个问题。TRPO的核心是利用单调改进定理,验证更新是否真正改进了我们的策略。
3.2.1 共轭梯度法(conjugate gradient method)
在自然策略梯度算法中,计算逆Fisher矩阵是一个耗时且数值不稳定的过程,特别是对于神经网络,参数矩阵可以变得非常大,
O
(
θ
3
)
O(\theta^3)
O(θ3)的时间复杂度将无法计算。
好消息是,我们对逆矩阵本身并不感兴趣。观察自然策略梯度的方程式,如果我们可以直接得到乘积
F
−
1
∇
l
o
g
π
θ
(
x
)
F^{-1}\nabla log{\pi_\theta}(x)
F−1∇logπθ(x),就不再需要逆。
引入共轭梯度法,这是一个近似上式乘积的数值过程,这样我们就可以避免计算逆矩阵。共轭梯度通常在
∣
θ
∣
|\theta|
∣θ∣步内收敛,从而可以处理大矩阵。
共轭梯度法并不是TRPO中独有的,例如在Truncated Natural Policy Gradient中也部署了相同的方法,但它仍然是算法中的一个重要组成部分。
3.2.2 线搜索(line search)
虽然自然梯度策略中提供了给定KL散度约束的最佳步长,但由于存在较多的近似值,实际上可能不满足该约束。
TRPO 通过执行线搜索来解决此问题,通过不断地迭代减小更新的大小,直到第一个不违反约束的更新。这个过程可以看作是不断缩小信任区域,即我们相信更新可以实际改进目标的区域。

图6. 线搜索算法
更新迭代减小的方式是使用指数衰减率
α
j
\alpha^j
αj,
j
j
j随迭代的进行而增加。同时,在约束条件的判断中,我们看到KL散度约束不是唯一满足的约束,它还保证了替代优势
L
(
θ
)
\mathcal{L}(\theta)
L(θ)非负,这就是接下来介绍的改进检查。
3.2.3 改进检查
在TRPO中,我们并没有假设更新会提高替代优势
L
(
θ
)
\mathcal{L}(\theta)
L(θ),而是真正检查了它。尽管实际计算时需要根据旧策略计算优势,以及使用重要性抽样来调整概率,会花费一些时间,但验证更新是否真正改进了策略是有必要的。
3.2.4 算法完整框架

图7. TRPO算法
TRPO执行了共轭梯度算法、约束样本KL散度的线搜索和检查改进替代优势,相较于自然策略梯度算法有了较大的改进,代表了自然策略梯度发展的一个重要里程碑。
4. 近端策略优化算法(PPO)
4.1 TRPO算法的缺陷
TRPO算法解决了许多与自然策略梯度相关的问题,并获得了RL社区的广泛采用。但是,TRPO仍然存在一些缺点,特别是:
- 无法处理大参数矩阵: 尽管使用了共轭梯度法,TRPO仍然难以处理大的 Fisher矩阵,即使它们不需要求逆
- 二阶优化很慢: TRPO的实际实现是基于约束的,需要计算上述Fisher矩阵,这大大减慢了更新过程。此外,我们不能利用一阶随机梯度优化器,例如ADAM
- TRPO 很复杂: TRPO很难解释、实现和调试。当训练没有产生预期的结果时,确定如何提高性能可能会很麻烦
在TRPO的基础上,Schulman等人引入了近端策略优化算法PPO(Proximal Policy Optimization)。有两种主要的PPO变体需要讨论(均在17年的论文中介绍):PPO Penalty和PPO Clip。我们首先从PPO Penalty入手,它在概念上最接近TRPO。
4.2 PPO Penalty
TRPO在理论分析上推导出与KL散度相乘的惩罚项,但在实践中,这种惩罚往往过于严格,只产生非常小的更新。因此,问题是如何可靠地确定缩放参数β ,同时避免overshooting:
Δ
θ
∗
=
argmax
Δ
θ
L
θ
+
Δ
θ
(
θ
+
Δ
θ
)
−
β
(
D
KL
(
π
θ
∥
π
θ
+
Δ
θ
)
)
\Delta\theta^*=\underset{\Delta\theta}{\operatorname{argmax}}\mathcal{L}_{\theta+\Delta\theta}({\theta}+\Delta\theta)-\beta(\mathcal{D}_{\operatorname{KL}}({\pi}_\theta\parallel{\pi}_{\theta+{\Delta\theta}}))
Δθ∗=ΔθargmaxLθ+Δθ(θ+Δθ)−β(DKL(πθ∥πθ+Δθ))难点是很难确定适用于多个问题的某个
β
\beta
β值。事实上,即使是同一个问题,随着时间的推移,特征也可能发生变化。我们既不希望
β
\beta
β过大,与TRPO一样只产生较小的更新,也不希望
β
\beta
β过大,容易出现overshooting问题。
PPO通过设置目标散度
δ
\delta
δ的方式解决了这个问题,希望我们的每次更新都位于目标散度附近的某个地方。目标散度应该大到足以显著改变策略,但又应该小到足以使更新稳定。
每次更新后,PPO都会检查更新的大小。如果最终更新的散度超过目标散度的 1.5倍,则下一次迭代我们将加倍
β
\beta
β来更加重惩罚。相反,如果更新太小,我们将
β
\beta
β减半,从而有效地扩大信任区域。迭代更新的思路与TRPO线搜索有一些相似之处,但PPO搜索是在两个方向上都有效的,而TRPO是单向减小的。
这里基于超过目标值的1.5倍将
β
\beta
β加倍或减半并不是数学证明的结果,而是基于启发式确定的。我们会不时违反约束条件,但通过调整
β
\beta
β可以很快地纠正它。根据经验,PPO对数值设置是非常不敏感的。总之,我们牺牲了一些数学上的严谨性来使实际的效果更好。

图8. PPO Penalty算法
与自然策略梯度和TRPO算法相比,PPO更容易实现。同时,我们可以使用流行的随机梯度下降算法(如ADAM等)执行更新,并在更新太大或太小时调整惩罚。
总之,PPO比TRPO更容易使用,同时不失竞争力。PPO的第二种变体PPO Clip将会做的比PPO Penalty更好。
4.3 PPO Clip
Clipped PPO是目前最流行的PPO的变体,也是我们说PPO时默认的变体。PPO Clip相比于PPO Penalty效果更好,也更容易实现。
与PPO Penalty不同,与其费心随着时间的推移改变惩罚,PPO Clip直接限制策略可以改变的范围。我们重新定义了替代优势:
L
π
θ
C
L
I
P
(
π
θ
k
)
=
E
τ
∼
π
θ
[
∑
t
=
0
T
[
min
(
ρ
t
(
π
θ
,
π
θ
k
)
A
t
π
θ
k
,
c
l
i
p
(
ρ
t
(
π
θ
,
π
θ
k
)
,
1
−
ϵ
,
1
+
ϵ
)
A
t
π
θ
k
)
]
]
\mathcal{L}_{\pi_\theta}^{CLIP}(\pi_{\theta_k})=\mathbb{E}_{\tau\sim\pi_\theta}\left[\sum_{t=0}^T\left[\min\left(\rho_t(\pi_\theta,\pi_{\theta_k})A_t^{\pi_{\theta_k}},\mathrm{clip}(\rho_t(\pi_{\theta},\pi_{\theta_{k}}),1-\epsilon,1+\epsilon)A_t^{\pi_{\theta_k}}\right)\right]\right]
LπθCLIP(πθk)=Eτ∼πθ[t=0∑T[min(ρt(πθ,πθk)Atπθk,clip(ρt(πθ,πθk),1−ϵ,1+ϵ)Atπθk)]]其中,
ρ
t
\rho_t
ρt为重要性采样:
ρ
t
(
θ
)
=
π
θ
(
a
t
∣
s
t
)
π
θ
k
(
a
t
∣
s
t
)
\rho_t(\theta) = \frac{\pi_\theta(a_t\mid s_t)}{\pi_{\theta_k}(a_t\mid s_{t})}
ρt(θ)=πθk(at∣st)πθ(at∣st)clip为截断函数,当重要性采样超出规定的上或下限后,函数会返回对应的上或下限。

图9. clip替代优势示意图
项
(
1
−
ϵ
)
A
(1-\epsilon)A
(1−ϵ)A和
(
1
+
ϵ
)
A
(1+\epsilon)A
(1+ϵ)A不依赖于
θ
\theta
θ,产生的梯度为0。因此,可信区域之外的样本被有效地抛出,避免过大的更新。我们没有明确地限制策略更新本身,只是简单地忽略了过度偏离策略所带来的优势。和PPO Penalty一样,我们可以使用像ADAM等优化器来执行更新。
PPO Clip中根据优势的正负性以及重要性采样的范围,可以分为六种可能的案例,在下图中对六种案例进行了总结。

图10. PPO Clip六种可能案例的总结
为了实现想要达到的效果,我们应该调整
ϵ
\epsilon
ϵ,作为对KL散度的隐式限制。根据经验,
ϵ
=
0.1
\epsilon=0.1
ϵ=0.1和
ϵ
=
0.2
\epsilon=0.2
ϵ=0.2是实际效果较好的值。尽管这些值与自然策略梯度的理论基础有些偏差(该理论建立在假设
π
θ
=
π
θ
k
\pi_\theta=\pi_{\theta_k}
πθ=πθk的局部近似值之上),但在实际运行时的效果较好。

图11. PPO Clip算法
4.4 PPO2
PPO2是Open AI发布的算法更新版本,是矢量化环境的PPO算法实现,针对 GPU 进行了优化,更好地支持并行训练。它与PPO也有许多实际实现的差异,例如优势被自动归一化、价值函数被裁剪等,但与本文概述的PPO具有相同的数学基础。如果需要直接使用OpenAI实现的PPO算法,则应该使用PPO2。
5. 总结
从传统策略梯度算法,到自然策略梯度算法,再到TRPO算法,以及最终的PPO算法,经过不断的优化迭代,PPO算法已经成为强化学习领域最主流的算法。不论是学术界中的各大顶会文章,还是工业界中例如chatgpt的背后强化学习部分的实现,都离不开PPO算法的身影。
纵向来看,对策略梯度算法的改进,主要针对的就是限制参数迭代的这一步。自然策略梯度算法引入了KL散度约束,TRPO利用线搜索和改进检查来保证限制下的可行性,PPO则通过clip函数限制了策略可以改变的范围等。
相比于自然梯度和TRPO所具有的理论保证和数学技巧,PPO放弃了一些数学上的严谨性,但往往能比其竞争对手更快更好地收敛。看来PPO在速度、严谨性和可用性之间取得了正确的平衡,在未来几年来依旧会保有属于它的竞争力。
参考文献
版权归原作者 PPPerry_1 所有, 如有侵权,请联系我们删除。