Abstract
我们提出了一种有趣的简单方法,用于在黑盒环境中构建对抗性图像。 与白盒场景相比,构建黑盒对抗图像对查询预算有额外的限制,而有效的攻击至今仍是一个悬而未决的问题。 仅在连续值置信分数的温和假设下,我们的高效查询算法利用了以下简单的迭代原理: 我们从预定义的正交基中随机采样向量,并将其添加或减去到目标图像中。 尽管简单,但所提出的方法既可以用于无目标攻击,也可以用于有目标攻击,这在两种设置中都带来了前所未有的查询效率。 我们在包括Google Cloud Vision API在内的多个现实环境中演示了我们算法的有效性和效率。 我们认为,我们提出的算法应该作为未来黑盒攻击的强大基线,特别是因为它非常快,而且它的实现需要不到20行PyTorch代码。
Introduction
随着机器学习系统在众多应用领域中的流行,这些系统在恶意对手面前的安全性成为一个重要的研究领域。 最近的许多研究表明,机器学习模型输出的决策可以通过对输入的细微改变而任意改变。这些对机器学习模型的攻击可以根据对手的功能进行分类。 白盒攻击要求对手完全了解目标模型,而黑盒攻击只需要对可能返回完整或部分信息的目标模型进行查询。
似乎所有用于自然图像分类的模型都容易受到白盒攻击。这表明自然图像倾向于接近由机器学习分类器学习的决策边界。 尽管经常被误解为神经网络的一种特性,但对抗性示例的脆弱性很可能是在具有大多数数据分布的高维空间中分类器的必然性。如果敌对的例子(几乎)总是存在,那么攻击分类器就变成了在目标图像周围的小范围内的搜索问题。
在白盒场景中,可以通过梯度下降有效地引导搜索。然而,黑匣子威胁模型在许多场景中更适用。 对模型的查询可能会导致大量的时间和金钱成本,因此,对模型进行的黑盒查询的数量是攻击算法效率的重要度量。 代价太高或很容易被查询限制击败的攻击比高效攻击带来的安全风险更小。 迄今为止,尽管最近在这方面做了大量工作,但最著名的黑盒攻击执行的平均查询数量仍然很高。最有效和最复杂的攻击通常仍然需要多达数万或数十万的查询。 一种查询效率高的黑盒攻击方法仍然是一个悬而未决的问题。
机器学习服务,如Clarifai或Google Cloud Vision,只允许API调用访问模型的预测,因此属于黑盒类。这些服务不发布任何内部细节,如培训数据和模型参数; 然而,他们的预测返回了连续值的置信分数。 在本文中,我们提出了一种简单但高效的黑箱攻击,它使用非常简单的直觉利用这些置信度得分: 如果到决策边界的距离很小,我们就不必过于小心我们朝着它行进的确切方向。
具体地说,我们在预先指定的一组正交搜索方向中重复选择一个随机方向,使用置信度分数检查它是否指向或远离决策边界,并通过从图像中添加或减去向量来扰动图像。 每次更新都会使图像进一步远离原始图像并朝向决策边界移动。
我们对我们的方法的有效性提供了一些理论见解,并评估了各种正交搜索子空间。 与Guo类似,我们观察到将搜索限制在离散余弦变换(DCT)基的低频端是特别有效的查询。 此外,我们通过经验证明,我们的方法实现了与最先进的黑盒攻击算法相似的成功率,但黑盒查询的数量空前少。 由于其简单性,它可以在PyTorch中用不到20行代码1实现。我们认为我们的方法是对抗性图像攻击的一种新的、可能令人惊讶的强大基线,我们称之为简单黑盒攻击(SimBA)。
Background
对抗性示例的研究涉及机器学习模型对输入中的小变化的鲁棒性。 图像分类的任务被定义为成功地预测人类在图像中看到的内容。 自然地,对图像的微小改变不会影响标签和预测。 我们可以将这种鲁棒性形式化如下: 模型,输入标签对(
)。模型可以正确分类
。h被称为关于可感知度量的ρ-鲁棒性
当
度量d通常近似为L0、L2和L∞ 测量干净输入和扰动输入
之间的视觉不相似度的距离。本文中除特殊提出,则使用以下作为度量标准
因此,几何上,不可察觉的变化区域被定义为半径为ρ的小超球面,以输入图像x为中心。最近,许多研究表明,即使ρ值很小,学习模型也承认非鲁棒性方向???。通过证明对抗性示例在高维空间中是固有的,理论上验证了这一说法。 这些发现激发了寻找对抗方向δ的问题,该方向改变了模型对扰动输入=
+ δ 的决策。
有针对性和无针对性的攻击。对手最简单的成功条件是将模型的原始正确预测更改为任意类,即h(x0)6=y。这被称为无目标攻击。相比之下,目标攻击旨在为某些选定的目标类y0构造x0,使得h(x0)=y0。为了简洁起见,我们将在讨论中重点讨论非目标攻击,但本文中的所有论点也适用于目标攻击。我们在第4节中包含了两种攻击类型的实验结果。
损失最小化。由于模型输出离散决策,因此首先,寻找对抗性扰动来改变模型的预测是一个离散优化问题。然而,定义替代损失y(·)通常是有用的,它测量模型h将输入分类为y类的确定程度。因此,对抗性扰动问题可以表述为以下最小化模型分类确定性的约束连续优化问题:
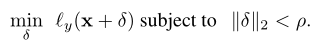
当模型h输出与每个类别相关的概率ph(·|x)时,一个常用的对抗性损失是类别y的概率:,基本上最小化了正确分类的概率。对于针对标签y'的目标攻击,常见的选择是
,基本上最大化错误分类为y'类的概率。
白盒威胁模型。根据应用领域,攻击者可能对目标模型h有不同程度的了解。在白盒威胁模型下,向对手提供分类器h。在这种情况下,一种强大的攻击策略是对对抗性损失y(·)或其近似值执行梯度下降。为了确保变化保持不可察觉,可以通过提前停止(Goodfellow et al.,2015;Kurakin et al.,2016)或通过将范数直接作为正则化或约束纳入损失优化(Carlini&Wagner,2017b)来控制扰动范数L2。
黑匣子威胁模型。可以说,对于许多现实世界的设置,白盒假设可能是不现实的。例如,模型h可以作为API公开给公众,只允许对输入进行查询。当攻击机器学习云服务(如Google cloud Vision和Clarifai)时,此类场景很常见。这种黑匣子威胁模型对对手来说更具挑战性,因为梯度信息可能无法用于指导寻找对抗方向δ,并且对模型的每次查询都会产生时间和金钱成本。因此,对手的任务是将黑箱查询的数量最小化到h,同时成功构建一个难以察觉的对抗性扰动。
稍微滥用符号,这就产生了一个修改的约束优化问题:
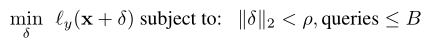
其中B是优化期间允许的查询数量的一些固定预算。对于查询的迭代方法,预算B限制了算法可能需要的迭代次数,因此要求攻击算法非常快速地收敛到解。
A Simple Black-box Attack
参数说明x图像数据y分类结果h(x) = y分类模型P(y|x)分类为y类别的概率δ最小波动q方向ε步长Q正交搜索方向集||δ||2波动的L2范数T最大步长
我们假设我们有一些图像x,黑箱神经网络h用预测的置信度或输出概率ph(y|x)对h(x)=y进行分类。我们的目标是找到一个小的扰动δ,使得预测。尽管黑箱设置中没有梯度信息,但我们认为输出概率的存在可以作为指导对抗图像搜索的强大代理。

算法。我们方法背后的直觉很简单(见算法1中的伪代码):对于任何方向q和某个步长,x+
q或 x-
q可能会降低ph(y|x)。因此,我们反复选择随机方向q,并将其相加或相减。为了最小化对h(·)的查询数量,我们总是首先尝试添加
q、 如果这降低了概率ph(y|x),我们就采取步骤,否则我们尝试-
q、 此过程平均每次更新需要1.4到1.5个查询(取决于数据集和目标模型)。
我们提出的方法——简单黑盒攻击(SimBA)——将目标图像标签对(x,y)、一组正交候选向量Q和步长>0作为输入。为简单起见,我们选择q∈ Q均匀随机。为了保证最大的查询效率,我们确保没有两个方向相互抵消并减少进度,或者相互放大并不成比例地增加δ的范数。出于这个原因,我们选择q而不进行替换,并将q中的所有向量限制为正交。如我们稍后所示,这导致了
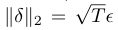 在T更新之后。 SimBA的唯一超参数是正交搜索向量集Q和步长。
在T更新之后。 SimBA的唯一超参数是正交搜索向量集Q和步长。
- 在正交搜索子空间中随机选取一个方向
- 进行“加”操作 - 如果P(y|x)变小,则继续进行“加”操作- 如果P(y|x)变大,则进行“减”操作
- 重复上述过程
笛卡尔基础。正交搜索方向集合Q的自然首选是标准基Q=I,这对应于直接在像素空间中执行我们的算法。本质上,每次迭代我们都在增加或减少单个随机选择像素的一种颜色。在此基础上的攻击对应于L0攻击,对手的目标是尽可能少地改变像素。
Q
离散余弦基。最近的研究发现,低频空间中的随机噪声更有可能是对抗性的。为了利用这一事实,我们跟随Guo等人(2018),并提出利用离散余弦变换(DCT)。离散余弦变换是一种正交变换,它将2D图像空间Rd×d中的信号映射到对应于余弦波函数大小的频率系数。在下文中,我们将DCT提取的正交频率集称为QDCT。虽然全套方向QDCT包含d×d频率,但我们只保留最低频率方向的一小部分r,以便在低频空间中进行对抗性扰动。
文献同时尝试SimBA(基于原图像像素空间)和SimBA-DCT(基于离散余弦变换低频空间),并作了比较分析。
一般依据。一般来说,我们认为,只要能够有效地对基向量进行采样,我们的攻击就可以用于任何正交基。这对于高分辨率数据集(如ImageNet)尤其具有挑战性,因为每个正交基向量都具有维数d×d。由于采样向量数量的线性内存成本,无法使用迭代采样方法(如Gram-Schmidt过程)。因此,我们选择仅使用标准基向量和DCT基向量来评估我们的攻击,以了解它们的效率和对图像的自然适应性。
学习率。给定任意一组搜索方向Q,某些方向可能比其他方向更能降低ph(y|x)。此外,输出概率ph(y|x+q)在
中可能是非单调的。在图1中,对于像素空间和DCT空间中的随机采样搜索方向,我们将概率的相对降低绘制为
的函数。概率对应于ResNet-50模型对ImageNet验证样本的预测。该图突出了一个启发性的结果:概率ph(y|x±
q)在
具有惊人的一致性(跨越随机图像和向量q)!虽然某些方向最终会增加真实等级概率,但这种概率的预期变化是负的,斜率相对较陡。这意味着我们的算法对epsilon的选择不太敏感,迭代将很快降低真正的类概率。该图还表示 DCT空间中的搜索倾向于导致比像素空间更陡峭的下降方向。 正如我们在下一节中所展示的,我们可以在给定epsilon的选择和最大步数T的情况下严格约束扰动的最终L2范数,因此ep的选择主要取决于关于L2的预算考虑。
预算考虑。通过利用基Q的正交性,我们可以严格地约束δ的范数。每次迭代都会增加、减去或丢弃一个基向量(如果两个方向都不能减少输出概率)。 表示在步骤t选择的搜索方向的符号,因此
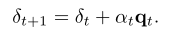
版权归原作者 偷懒不学习 所有, 如有侵权,请联系我们删除。