GHostNet网络最通俗易懂的解读【不接受反驳】

文章目录

前沿知识

在介绍GHostNet网络之前，我们首先回顾一下分组卷积和深度可分离卷积。

分组卷积

假设input.shape = [

      C
     
     
      1
     
    
   
   
    C_1
   
  
 C1​, H, W] output.shape = 
 
  
   
    
     [
    
    
     
      C
     
     
      2
     
    
    
     ,
    
    
     
      H
     
     
      1
     
    
    
     ,
    
    
     
      W
     
     
      1
     
    
    
     ]
    
   
   
    [C_2, H^1, W^1]
   
  
 [C2​,H1,W1]

输入每组feature map尺寸：

     W
    
    
     ×
    
    
     H
    
    
     ×
    
    
     
      
       C
      
      
       1
      
     
     
      g
     
    
   
   
    W×H× \frac {C_1} {g}
   
  
 W×H×gC1​​ ，共有g组。

单个卷积核每组的尺寸：

     k
    
    
     ×
    
    
     k
    
    
     ×
    
    
     
      
       C
      
      
       2
      
     
     
      g
     
    
   
   
    k×k×\frac {C_2} {g}
   
  
 k×k×gC2​​，一个卷积核被分成了g组。

输出feature map尺寸：

      W
     
     
      1
     
    
    
     ×
    
    
     
      H
     
     
      1
     
    
    
     ×
    
    
     g
    
   
   
    W^1×H^1×g
   
  
 W1×H1×g，共生成g个feature map。

**

现在我们计算一下分组卷积时的参数量和运算量：

**
参数量

     p
    
    
     a
    
    
     r
    
    
     a
    
    
     m
    
    
     s
    
    
     =
    
    
     
      k
     
     
      2
     
    
    
     ×
    
    
     
      
       C
      
      
       1
      
     
     
      g
     
    
    
     ×
    
    
     
      
       C
      
      
       2
      
     
     
      g
     
    
    
     ×
    
    
     g
    
    
     =
    
    
     
      k
     
     
      2
     
    
    
     
      
       C
      
      
       1
      
     
     
      g
     
    
    
     
      C
     
     
      2
     
    
   
   
    params=k^2×\frac {C_1} {g}×\frac{C_2}{g}\times g=k^2\frac{C_1}{g} C_2
   
  
 params=k2×gC1​​×gC2​​×g=k2gC1​​C2​

运算量

     F
    
    
     L
    
    
     O
    
    
     P
    
    
     s
    
    
     =
    
    
     
      k
     
     
      2
     
    
    
     ×
    
    
     
      
       C
      
      
       1
      
     
     
      g
     
    
    
     
      C
     
     
      2
     
    
    
     ×
    
    
     
      W
     
     
      1
     
    
    
     ×
    
    
     
      H
     
     
      1
     
    
    
     =
    
    
     
      k
     
     
      2
     
    
    
     
      
       C
      
      
       1
      
     
     
      g
     
    
    
     
      C
     
     
      2
     
    
    
     
      W
     
     
      1
     
    
    
     
      H
     
     
      1
     
    
   
   
    FLOPs=k^2×\frac {C_1} {g} C_2×W^1×H^1=k^2\frac{C_1}{g} C_2W^1H^1
   
  
 FLOPs=k2×gC1​​C2​×W1×H1=k2gC1​​C2​W1H1

• 分析： 利用分层过滤组提高CNN效率论文地址 官方分析：Alex认为group conv的方式能够增加 filter之间的对角相关性,而且能够减少训练参数,不容易过拟合,这类似于正则的效果。
• 代码实现(pytorch提供了相关参数,以2d为例)

import torch
import torch.nn as nn
...
model = nn.Conv2d(in_channels = in_channel, out_channels = out_channel, 
kernel_size = kernel_size, stride = stride, padding =1, dilation = dilation, group = group_num)

通过上述的代码我们可以清楚的看见

分组卷积

就做了一次卷积。

深度可分离卷积

MobileNets:论文地址
深度可分离卷积是MobileNet的精髓,它由deep_wise卷积和point_wise卷积两部分组成。我以前一直觉得深度可分离卷积是极端化的分组卷积(把group数量设为Cin个就行)。但今天再次思考一下,发现他们很大的不同在于,分组卷积只进行一次卷积(一个nn.Conv2d即可实现),不同group的卷积结果concat即可,而深度可分离卷积是进行了两次卷积操作,第一次先进行deep_wise卷积(即收集每一层的特征),kernel_size = KK1,第一次卷积总的参数量为KKCin,第二次是为了得到Cout维度的输出,kernel_size = 11Cin,第二次卷积总的参数量为11Cin*Cout。第二次卷积输出即为深度可分离卷积的输出。

• 举例

举个例子比较参数量：假设input.shape = [

      c
     
     
      1
     
    
   
   
    c_1
   
  
 c1​, H, W] output.shape = [
 
  
   
    
     
      c
     
     
      2
     
    
   
   
    c_2
   
  
 c2​, H, W]

(a)常规卷积参数量=

     k
    
    
     ×
    
    
     k
    
    
     ×
    
    
     
      c
     
     
      1
     
    
    
     ×
    
    
     
      c
     
     
      2
     
    
   
   
    k \times k \times c_1 \times c_2
   
  
 k×k×c1​×c2​

(b)深度可分离卷积参数量=

     k
    
    
     ×
    
    
     k
    
    
     ×
    
    
     c
    
    
     1
    
    
     +
    
    
     1
    
    
     ×
    
    
     1
    
    
     ×
    
    
     
      c
     
     
      1
     
    
    
     ×
    
    
     
      c
     
     
      2
     
    
   
   
    k \times k \times c1 + 1\times1\times c_1\times c_2
   
  
 k×k×c1+1×1×c1​×c2​

上面的例子我们可以清楚地看到,得到相同的output.shape,直观看上去,深度可分离卷积的参数量比常规卷积少了一个数量级。

• 代码实现(pytorch)

import torch
import torch.nn as nn
...
model = nn.Sequential(
        nn.Conv2d(in_channels = in_channel, out_channels = in_channel, 
kernel_size = kernel_size, stride = stride, padding =1, dilation = dilation, group = in_channel),
        nn.Conv2d(in_channels = in_channel, out_channels = out_channel kernel_size =1, padding =0))

之所以在写在前面中提到,本文的题目一定要先是分组卷积再是深度可分离卷积,因为在我看来后者是前者的极端情况(分组卷积的

     g
    
    
     r
    
    
     o
    
    
     u
    
    
     p
    
   
   
    group
   
  
 group设为
 
  
   
    
     i
    
    
     
      n
     
     
      c
     
    
    
     h
    
    
     a
    
    
     n
    
    
     n
    
    
     e
    
    
     l
    
   
   
    in_channel
   
  
 inc​hannel,即每组的channel数量为1),尽管形式上两者有比较大的差别:分组卷积只进行一次卷积操作即可,而深度可分离卷积需要进行两次——先
 
  
   
    
     d
    
    
     e
    
    
     p
    
    
     t
    
    
     h
    
    
     −
    
    
     w
    
    
     i
    
    
     s
    
    
     e
    
   
   
    depth-wise
   
  
 depth−wise再
 
  
   
    
     p
    
    
     o
    
    
     i
    
    
     n
    
    
     t
    
    
     −
    
    
     w
    
    
     i
    
    
     s
    
    
     e
    
   
   
    point-wise
   
  
 point−wise卷积,但他们本质上是一样的。

深度可分离卷积进行一次卷积是无法达到输出指定维度的tensor的,这是由它将group设为in_channel决定的,输出的tensor通道数只能是in_channel,不能达到要求,所以又用了1*1的卷积改变最终输出的通道数。

这样的想法也是自然而然的,

     B
    
    
     o
    
    
     t
    
    
     t
    
    
     l
    
    
     e
    
    
     N
    
    
     e
    
    
     c
    
    
     k
    
   
   
    BottleNeck
   
  
 BottleNeck不就是先1*1卷积减少参数量再
  
   
    
     
      3
     
     
      ×
     
     
      3
     
    
    
     3\times 3
    
   
  3×3卷积feature map,最后再1*1恢复原来的通道数,所以
 
  
   
    
     B
    
    
     o
    
    
     t
    
    
     t
    
    
     l
    
    
     e
    
    
     N
    
    
     e
    
    
     c
    
    
     k
    
   
   
    BottleNeck
   
  
 BottleNeck的目的就是减少参数量。提到BottleNeck结构就是想说明1*1卷积经常用来改变通道数。

GHostNet网络

GHostNet论文地址
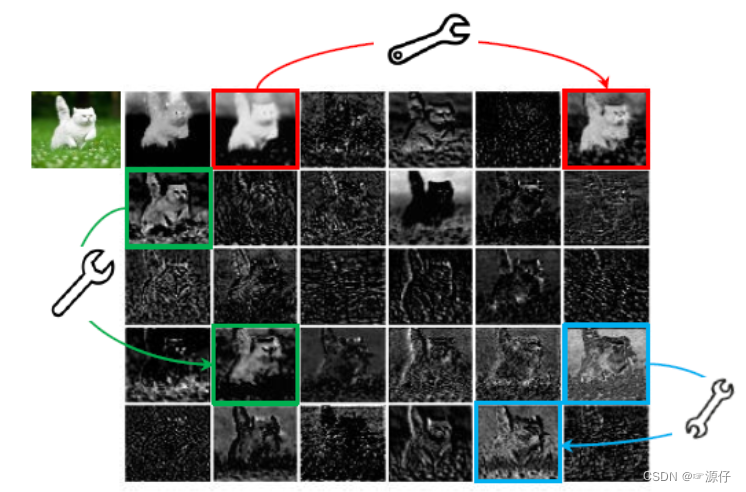
如下图所示，是由ResNet-50中的第一个残差块生成的某些中间特征图的可视化。从图中我们可以看出，这里面有很多特征图是具有高度相似性的（在图中分别用不同的颜色示意），换句话说，就是存在许多的冗余特征图。所以从另一个角度想，我们是不是可以利用一系列的线性变化，以很小的代价生成许多能从原始特征发掘所需信息的“幻影”特征图呢？（冗余的特征图是非常有必要的，可以保证网络对输入数据的理解更为全面。）这个便是整篇文章的核心思想。

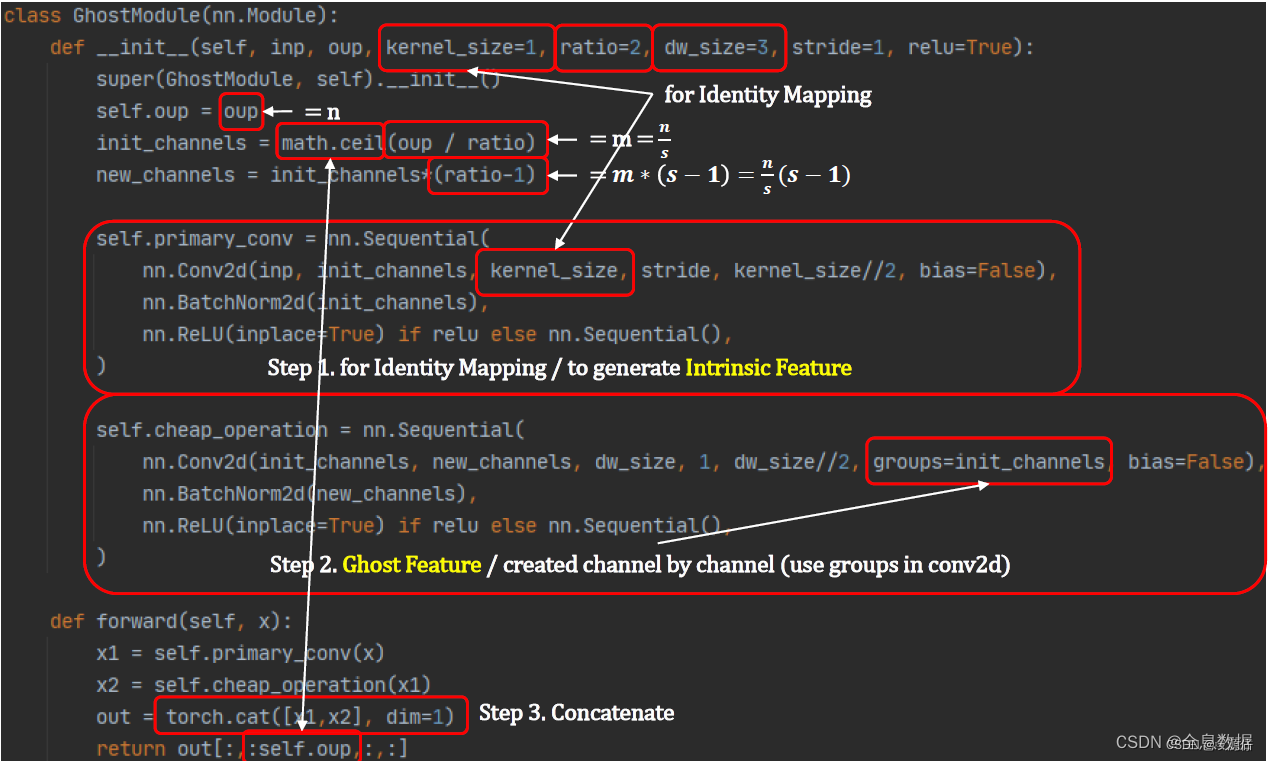
如下图，我把Ghost-Module分成三个部分：

• 第一部分就是一个普通的卷积操作，但是我们并没有把其的通道设置的很大，我们假设其输出通道数为 m ( m < n ) m(m<n) m(m<n)， n n n为 O u t p u t Output Output输出的通道数。
• 第二部分就是一个分组卷积操作，记住是分组卷积，很多博主写的是深度可分离卷积操作，上面我也提到了深度可分离卷积是分两步操作的，但是这里的代码就是一次卷积，这样就好理解了。通过第二部分的分组卷积操作我们可以得到 O u t p u t Output Output输出特征图下面红的的一部分特征图。
• 第三部分Identity，这个就很好理解了，就是把由第一部分卷积得到的通道数为 m m m的特征图与第二部分分组卷积得到的通道数为 ( m − 1 ) s (m-1)s (m−1)s的通道数相加。 其中, Φ i Φ_i Φi​ 为线性变换。实际操作中 Φ i Φ_i Φi​ 的变换方法不固定，可以是 3x3 线性核或者 5x5 线性核（其实有点类似深度卷积思想，但不同的是深度卷积前后的通道数相同，而这里 Φ i Φ_i Φi​ 可以产生所需要的通道数，并且可以对同一通道特征图进行多次线性变换【其实当 s 取 2 时， Φ i Φ_i Φi​ 就是原原本本的深度卷积】）。另外，理论上可以使用不同尺寸大小的卷积核组合进行线性变换操作，但考虑到 CPU 或 GPU 的推理情况，作者建议全部使用 3x3 卷积核或全部使用 5x5 卷积核。

代码

本张图片来自GhostNet 详解，首先我们可以知道Output的输出通道数为

    n
   
  
  
   n
  
 
n，通过

第一部分卷积

后的通道数为

    m
   
   
    =
   
   
    
     n
    
    
     s
    
   
  
  
   m = \frac{n}{s}
  
 
m=sn​，通过

第二部分

得到的输出通道为

    m
   
   
    ×
   
   
    (
   
   
    s
   
   
    −
   
   
    1
   
   
    )
   
   
    =
   
   
    
     n
    
    
     s
    
   
  
  
   m\times(s-1) = \frac{n}{s}
  
 
m×(s−1)=sn​，那么再通过

第三步

    I
   
   
    d
   
   
    e
   
   
    n
   
   
    t
   
   
    i
   
   
    t
   
   
    y
   
  
  
   Identity
  
 
Identity恒等映射把前面两部得到的特征图按通道数(dim = 1)进行相加，这样我们就可以得到

 
  
   
    O
   
   
    u
   
   
    t
   
   
    p
   
   
    u
   
   
    t
   
  
  
   Output
  
 
Output输出特征图且通道数为（

 
  
   
    c
   
   
    h
   
   
    a
   
   
    n
   
   
    n
   
   
    e
   
   
    l
   
   
    =
   
   
    m
   
   
    +
   
   
    m
   
   
    ×
   
   
    (
   
   
    s
   
   
    −
   
   
    1
   
   
    )
   
   
    =
   
   
    s
   
   
    ×
   
   
    m
   
  
  
   channel = m + m\times(s - 1) = s\times m
  
 
channel=m+m×(s−1)=s×m），又因为

 
  
   
    m
   
   
    =
   
   
    
     n
    
    
     s
    
   
  
  
   m = \frac{n}{s}
  
 
m=sn​，所以输出通道数还是

 
  
   
    n
   
  
  
   n
  
 
n。

GHost Module比普通卷积的优点

GHost Module模块

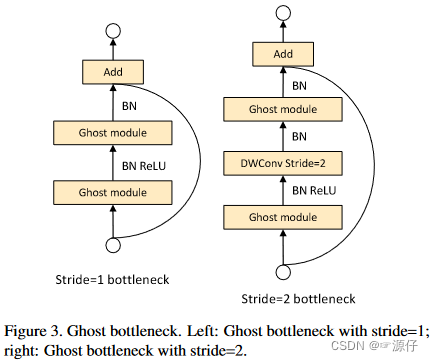
在一个 G-bneck 中存在两个 Ghost module ，其中第一个 Ghost module 用于增加通道数（expansion layer），指定输出和输入通道数之间的比例为扩张比。第二个 Ghost module 减少通道数以匹配 shortcut 分支的通道。当步长为 2 时，在两个 Ghost module 中间加入一个步长为 2 的深度卷积层。

参数量对比

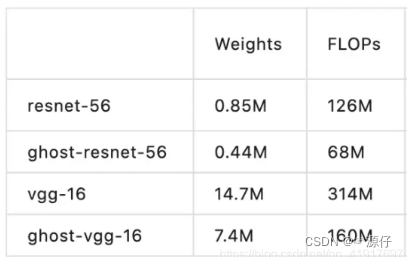
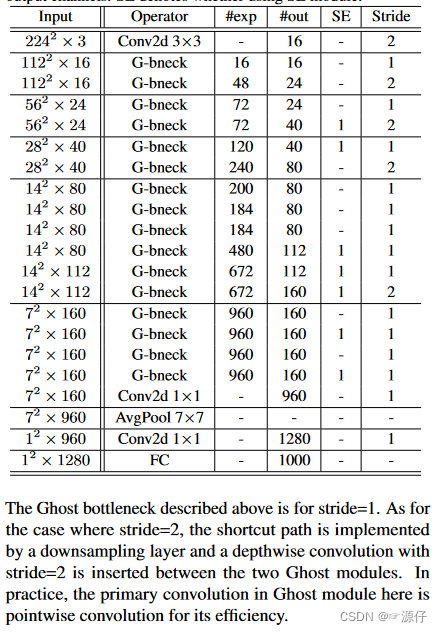
GHostNet网络结构