0
0

AI实战-Tensorflow使用 LSTM 进行股票市场预测 (完整步骤+源码讲解)

在本教程中，您将了解如何使用称为长短期记忆的时间序列模型。 LSTM 模型非常强大，特别是在设计上保留长期记忆，正如您稍后将看到的。您将在本教程中解决以下主题：

  • 了解为什么您需要能够预测股价走势；
  • 下载数据——您将使用从 Alphavantage/Kaggle 收集的股票市场数据；
  • 分割训练测试数据并执行一些数据标准化；
  • 激发并简要讨论 LSTM 模型，因为它可以提前预测不止一步；
  • 利用当前数据预测和可视化未来股市

注意：但在我们开始之前，我并不是主张 LSTM 作为一种高度可靠的模型，可以完美地利用股票数据中的模式，或者可以在没有任何人参与的情况下盲目使用。我这样做是为了纯粹的机器学习兴趣，作为一个实验。在我看来，该模型观察到了数据中的某些模式，从而使其能够在大多数情况下正确预测股票走势。但这个模型是否可以用于实际目的取决于您。

为什么需要时间序列模型？

您希望正确地对股票价格进行建模，以便作为股票购买者，您可以合理地决定何时购买股票以及何时出售股票以赚取利润。这就是时间序列建模的用武之地。您需要良好的机器学习模型，该模型可以查看数据序列的历史记录并正确预测序列的未来元素。

警告：股票市场价格高度不可预测且不稳定。这意味着数据中不存在一致的模式，无法让您近乎完美地对一段时间内的股票价格进行建模。不要从我这里听，而是从普林斯顿大学经济学家 Burton Malkiel 那里听，他在 1973 年的书中指出，“随机漫步华尔街”如果市场确实有效，并且股价一公开就立即反映了所有因素，那么一只蒙着眼睛的猴子向报纸上的股票投掷飞镖应该和任何投资专业人士一样好。

然而，我们不要完全相信这只是一个随机或随意的过程，并且机器学习没有希望。让我们看看您是否至少可以对数据进行建模，以便您所做的预测与数据的实际行为相关联。换句话说，您不需要未来的确切股票价值，而是股票价格走势（即，在不久的将来是否会上涨或下跌）。

# Make sure that you have all these libaries available to run the code successfully
from pandas_datareader import data
import matplotlib.pyplot as plt
import pandas as pd
import datetime as dt
import urllib.request, json 
import os
import numpy as np
import tensorflow as tf # This code has been tested with TensorFlow 1.6
from sklearn.preprocessing import MinMaxScaler

下载数据

您将使用以下来源的数据：

  1. 阿尔法优势。不过，在开始之前，您首先需要一个 API 密钥，您可以在此处免费获取该密钥。之后，您可以将该键分配给api_key变量。
  2. 使用此页面中的数据。您需要将zip 文件中的Stocks文件夹复制到项目主文件夹中。

股票价格有几种不同的表现。他们是，

  • 开盘价：当日股票开盘价
  • 收盘价：当日收盘价
  • High：数据中最高的股价
  • 最低价：当日最低股价

从 Alphavantage 获取数据

您将首先从 Alpha Vantage 加载数据。由于您将利用美国航空股票市场价格进行预测，因此您将股票代码设置为

"AAL"

。此外，您还定义了一个

url_string

，它将返回一个 JSON 文件，其中包含过去 20 年内美国航空的所有股票市场数据，以及一个

file_to_save

，它将是您保存数据的文件。您将使用

ticker

之前定义的变量来帮助命名该文件。

接下来，您将指定一个条件：如果您尚未保存数据，您将继续从您在 中设置的 URL 中获取数据

url_string

；您将把日期、最低价、最高价、交易量、收盘价、开盘价存储到 pandas DataFrame 中，

df

并将其保存到

file_to_save

.但是，如果数据已经存在，您只需从 CSV 加载即可。

从 Kaggle 获取数据

Kaggle 上找到的数据是 csv 文件的集合，您无需进行任何预处理，因此可以直接将数据加载到 Pandas DataFrame 中。确保将数据下载到项目主目录中。因此Stocks文件夹应该位于项目主目录中。

数据探索

在这里，您将把收集的数据打印到 DataFrame 中。您还应该确保数据按日期排序，因为数据的顺序在时间序列建模中至关重要。

# Sort DataFrame by date
df = df.sort_values('Date')

# Double check the result
df.head()

数据可视化

现在让我们看看您拥有什么类型的数据。您希望数据随着时间的推移而出现各种模式。

plt.figure(figsize = (18,9))
plt.plot(range(df.shape[0]),(df['Low']+df['High'])/2.0)
plt.xticks(range(0,df.shape[0],500),df['Date'].loc[::500],rotation=45)
plt.xlabel('Date',fontsize=18)
plt.ylabel('Mid Price',fontsize=18)
plt.show()

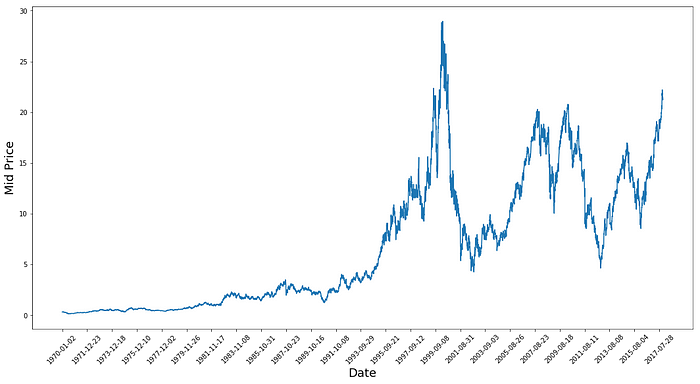
这张图已经说明了很多事情。我选择这家公司而不是其他公司的具体原因是，随着时间的推移，这张图表充满了股票价格的不同行为。这将使学习更加稳健，并为您提供一个改变来测试各种情况下的预测效果如何。

另一件值得注意的事情是，接近 2017 年的值比接近 1970 年代的值要高得多，波动也更大。因此，您需要确保数据在整个时间范围内表现在相似的值范围内。您将在数据标准化阶段处理这个问题。

将数据拆分为训练集和测试集

您将使用通过一天的最高记录价格和最低记录价格的平均值计算出的中间价格。

# First calculate the mid prices from the highest and lowest
high_prices = df.loc[:,'High'].as_matrix()
low_prices = df.loc[:,'Low'].as_matrix()
mid_prices = (high_prices+low_prices)/2.0

现在您可以拆分训练数据和测试数据。训练数据将是时间序列的前 11,000 个数据点，其余数据将是测试数据。

现在您需要定义一个缩放器来标准化数据。

MinMaxScalar

将所有数据缩放到 0 和 1 的区域内。您还可以将训练和测试数据重塑为形状

[data_size, num_features]

。

# Scale the data to be between 0 and 1
# When scaling remember! You normalize both test and train data with respect to training data
# Because you are not supposed to have access to test data
scaler = MinMaxScaler()
train_data = train_data.reshape(-1,1)
test_data = test_data.reshape(-1,1)

由于您之前进行的观察，即不同时间段的数据具有不同的值范围，因此您通过将整个系列拆分为窗口来对数据进行归一化。如果不这样做，早期的数据将接近于 0，并且不会为学习过程增加太多价值。这里您选择窗口大小 2500。

提示：选择窗口大小时，请确保它不要太小，因为当您执行窗口归一化时，它可能会在每个窗口的最后引入一个中断，因为每个窗口都是独立归一化的。

在此示例中，4 个数据点将受此影响。但考虑到您有 11,000 个数据点，4 个点不会造成任何问题

# Train the Scaler with training data and smooth data
smoothing_window_size = 2500
for di in range(0,10000,smoothing_window_size):
    scaler.fit(train_data[di:di+smoothing_window_size,:])
    train_data[di:di+smoothing_window_size,:] = scaler.transform(train_data[di:di+smoothing_window_size,:])

# You normalize the last bit of remaining data
scaler.fit(train_data[di+smoothing_window_size:,:])
train_data[di+smoothing_window_size:,:] = scaler.transform(train_data[di+smoothing_window_size:,:])

将数据重塑回形状

[data_size]

# Reshape both train and test data
train_data = train_data.reshape(-1)

# Normalize test data
test_data = scaler.transform(test_data).reshape(-1)

您现在可以使用指数移动平均线来平滑数据。这可以帮助您摆脱股票价格数据固有的不规则性并产生更平滑的曲线。

注意：我们仅使用训练数据来训练 MinMaxScaler，通过将 MinMaxScaler 拟合到测试数据来标准化测试数据是错误的

请注意，您应该只平滑训练数据。

# Now perform exponential moving average smoothing
# So the data will have a smoother curve than the original ragged data
EMA = 0.0
gamma = 0.1
for ti in range(11000):
  EMA = gamma*train_data[ti] + (1-gamma)*EMA
  train_data[ti] = EMA

# Used for visualization and test purposes
all_mid_data = np.concatenate([train_data,test_data],axis=0)

评估结果

我们将使用均方误差来计算我们的模型有多好。均方误差 (MSE) 可以通过向前一步的真实值与预测值之间的平方误差计算，并对所有预测进行平均。

平均作为股票价格建模技术

在最初的教程中，我讨论了对于此类问题来说，平均是如何具有欺骗性和糟糕的。结论是，

平均可以很好地预测提前一步（这对于股票市场预测不是很有用），但对未来的预测却不太有效。您可以在原始教程中找到更多详细信息。

LSTM 简介：预测未来的股票走势

长短期记忆模型是极其强大的时间序列模型。他们可以预测未来的任意数量的步骤。 LSTM 模块（或单元）具有 5 个基本组件，使其能够对长期和短期数据进行建模。

  • 单元状态 (c_t) — 这表示单元的内部存储器，存储短期记忆和长期记忆
  • 隐藏状态 (h_t) — 这是根据当前输入、先前隐藏状态和当前单元输入计算的输出状态信息，最终用于预测未来的股票市场价格。此外，隐藏状态可以决定仅检索存储在单元状态中的短期或长期或两种类型的记忆来进行下一个预测。
  • 输入门 (i_t) — 决定当前输入有多少信息流向单元状态
  • 遗忘门 (f_t) — 决定当前输入和先前单元状态中的多少信息流入当前单元状态
  • 输出门 (o_t) — 决定有多少信息从当前单元状态流入隐藏状态，以便在需要时 LSTM 只能选择长期记忆或短期记忆和长期记忆

下图是一个单元格。

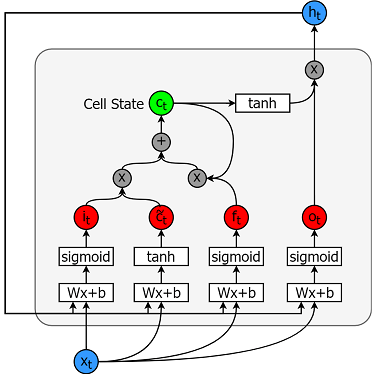
计算每个实体的方程式如下。

  • i _t = σ (W {ix} * x _t + W {ih} * h_{t-1}+b_i)
  • \tilde{c} _t = σ (W {cx} * x _t + W {ch} * h_{t-1} + b_c)
  • f _t = σ (W {fx} * x t + W {fh} * h_{t-1}+b_f)
  • c_t = f _t * c {t-1} + i_t * \tilde{c}_t
  • o _t = σ (W {ox} * x t + W {oh} * h_{t-1}+b_o)
  • h_t = o_t * tanh(c_t)

为了更好（更技术性）地理解 LSTM，您可以参考这篇文章。

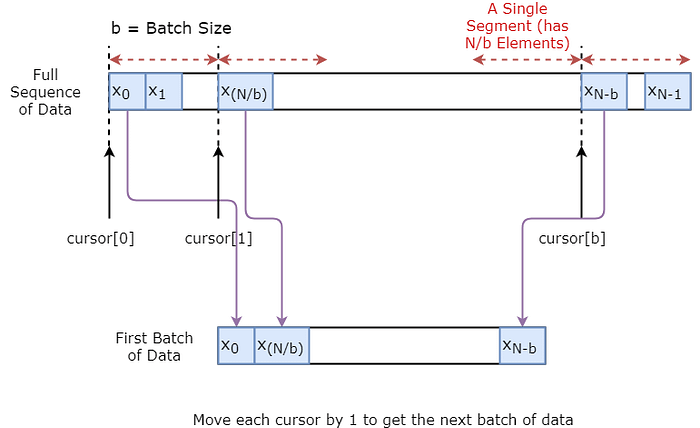
数据生成器

下面您将说明如何直观地创建一批数据。基本思想是我们将数据序列分为N/b段，使得每个段的大小为b。然后我们定义游标，每个段1个。然后，为了对一批数据进行采样，我们得到一个输入（当前段光标索引）和一个真实预测（在 [当前段光标 + 1，当前段光标 + 5] 之间随机采样一个）。请注意，我们并不总是获得输入旁边的值作为其预测。这是为了减少过度拟合而采取的步骤。在每次采样结束时，我们将光标增加 1。您可以在原始教程中找到有关数据生成的更多信息。

定义超参数

在本部分中，您将定义几个超参数。

D

是输入的维数。这很简单，因为您将前一个股票价格作为输入并预测下一个股票价格，应该是

1

。

那么

num_unrollings

， 表示您为单个优化步骤考虑的连续时间步骤数。越大越好。

然后你就拥有了

batch_size

.批量大小是您在单个时间步中考虑的数据样本数量。越大越好，因为在给定时间您拥有的数据的可见性更高。

接下来，您定义

num_nodes

代表每个单元中隐藏神经元的数量。您可以看到此示例中有三层 LSTM。

D = 1 # Dimensionality of the data. Since your data is 1-D this would be 1
num_unrollings = 50 # Number of time steps you look into the future.
batch_size = 500 # Number of samples in a batch
num_nodes = [200,200,150] # Number of hidden nodes in each layer of the deep LSTM stack we're using
n_layers = len(num_nodes) # number of layers
dropout = 0.2 # dropout amount

tf.reset_default_graph() # This is important in case you run this multiple times

定义输入和输出

接下来，您定义训练输入和标签的占位符。这非常简单，因为您有一个输入占位符列表，其中每个占位符都包含一批数据。该列表具有

num_unrollings

占位符，将立即用于单个优化步骤。

# Input data.
train_inputs, train_outputs = [],[]

# You unroll the input over time defining placeholders for each time step
for ui in range(num_unrollings):
    train_inputs.append(tf.placeholder(tf.float32, shape=[batch_size,D],name='train_inputs_%d'%ui))
    train_outputs.append(tf.placeholder(tf.float32, shape=[batch_size,1], name = 'train_outputs_%d'%ui))

定义 LSTM 和回归层的参数

您将拥有三层 LSTM 和一个线性回归层（用

w

和表示

b

），它获取最后一个长短期记忆单元的输出并输出下一个时间步的预测。您可以使用

MultiRNNCell

TensorFlow 中的 来封装您创建的三个

LSTMCell

对象。此外，您可以让 dropout 实现 LSTM 单元，因为它们可以提高性能并减少过度拟合。

lstm_cells = [
    tf.contrib.rnn.LSTMCell(num_units=num_nodes[li],
                            state_is_tuple=True,
                            initializer= tf.contrib.layers.xavier_initializer()
                           )
 for li in range(n_layers)]

drop_lstm_cells = [tf.contrib.rnn.DropoutWrapper(
    lstm, input_keep_prob=1.0,output_keep_prob=1.0-dropout, state_keep_prob=1.0-dropout
) for lstm in lstm_cells]
drop_multi_cell = tf.contrib.rnn.MultiRNNCell(drop_lstm_cells)
multi_cell = tf.contrib.rnn.MultiRNNCell(lstm_cells)

w = tf.get_variable('w',shape=[num_nodes[-1], 1], initializer=tf.contrib.layers.xavier_initializer())
b = tf.get_variable('b',initializer=tf.random_uniform([1],-0.1,0.1))

计算 LSTM 输出并将其馈送到回归层以获得最终预测

在本部分中，您首先创建 TensorFlow 变量 (

c

和

h

)，用于保存长短期记忆单元的单元状态和隐藏状态。然后将 的列表转换

train_inputs

为 的形状

[num_unrollings, batch_size, D]

，这是使用函数计算输出所需要的

tf.nn.dynamic_rnn

。然后，您使用该函数计算 LSTM 输出

tf.nn.dynamic_rnn

，并将输出拆分回张量列表

num_unrolling

。预测与真实股票价格之间的损失。

# Create cell state and hidden state variables to maintain the state of the LSTM
c, h = [],[]
initial_state = []
for li in range(n_layers):
  c.append(tf.Variable(tf.zeros([batch_size, num_nodes[li]]), trainable=False))
  h.append(tf.Variable(tf.zeros([batch_size, num_nodes[li]]), trainable=False))
  initial_state.append(tf.contrib.rnn.LSTMStateTuple(c[li], h[li]))

# Do several tensor transofmations, because the function dynamic_rnn requires the output to be of
# a specific format. Read more at: https://www.tensorflow.org/api_docs/python/tf/nn/dynamic_rnn
all_inputs = tf.concat([tf.expand_dims(t,0) for t in train_inputs],axis=0)

# all_outputs is [seq_length, batch_size, num_nodes]
all_lstm_outputs, state = tf.nn.dynamic_rnn(
    drop_multi_cell, all_inputs, initial_state=tuple(initial_state),
    time_major = True, dtype=tf.float32)

all_lstm_outputs = tf.reshape(all_lstm_outputs, [batch_size*num_unrollings,num_nodes[-1]])

all_outputs = tf.nn.xw_plus_b(all_lstm_outputs,w,b)

split_outputs = tf.split(all_outputs,num_unrollings,axis=0)

损失计算和优化器

现在，您将计算损失。但是，您应该注意，计算损失时有一个独特的特征。对于每批预测和真实输出，您计算均方误差。然后将所有这些均方损失相加（不是平均）。最后，您定义将用于优化神经网络的优化器。在这种情况下，您可以使用 Adam，这是一个非常新且性能良好的优化器。

 When calculating the loss you need to be careful about the exact form, because you calculate
# loss of all the unrolled steps at the same time
# Therefore, take the mean error or each batch and get the sum of that over all the unrolled steps

print('Defining training Loss')
loss = 0.0
with tf.control_dependencies([tf.assign(c[li], state[li][0]) for li in range(n_layers)]+
                             [tf.assign(h[li], state[li][1]) for li in range(n_layers)]):
  for ui in range(num_unrollings):
    loss += tf.reduce_mean(0.5*(split_outputs[ui]-train_outputs[ui])**2)

print('Learning rate decay operations')
global_step = tf.Variable(0, trainable=False)
inc_gstep = tf.assign(global_step,global_step + 1)
tf_learning_rate = tf.placeholder(shape=None,dtype=tf.float32)
tf_min_learning_rate = tf.placeholder(shape=None,dtype=tf.float32)

learning_rate = tf.maximum(
    tf.train.exponential_decay(tf_learning_rate, global_step, decay_steps=1, decay_rate=0.5, staircase=True),
    tf_min_learning_rate)

# Optimizer.
print('TF Optimization operations')
optimizer = tf.train.AdamOptimizer(learning_rate)
gradients, v = zip(*optimizer.compute_gradients(loss))
gradients, _ = tf.clip_by_global_norm(gradients, 5.0)
optimizer = optimizer.apply_gradients(
    zip(gradients, v))

print('\tAll done')

您可以在此处定义与预测相关的 TensorFlow 操作。首先，定义用于输入输入的占位符 ( 

sample_inputs

)，然后与训练阶段类似，定义用于预测的状态变量 (

sample_c

和

sample_h

)。最后，您使用该函数计算预测，然后通过回归层（和）

tf.nn.dynamic_rnn

发送输出。您还应该定义重置单元状态和隐藏状态的操作。每次进行一系列预测时，您都应该在开始时执行此操作。

w

b

reset_sample_state

print('Defining prediction related TF functions')

sample_inputs = tf.placeholder(tf.float32, shape=[1,D])

# Maintaining LSTM state for prediction stage
sample_c, sample_h, initial_sample_state = [],[],[]
for li in range(n_layers):
  sample_c.append(tf.Variable(tf.zeros([1, num_nodes[li]]), trainable=False))
  sample_h.append(tf.Variable(tf.zeros([1, num_nodes[li]]), trainable=False))
  initial_sample_state.append(tf.contrib.rnn.LSTMStateTuple(sample_c[li],sample_h[li]))

reset_sample_states = tf.group(*[tf.assign(sample_c[li],tf.zeros([1, num_nodes[li]])) for li in range(n_layers)],
                               *[tf.assign(sample_h[li],tf.zeros([1, num_nodes[li]])) for li in range(n_layers)])

sample_outputs, sample_state = tf.nn.dynamic_rnn(multi_cell, tf.expand_dims(sample_inputs,0),
                                   initial_state=tuple(initial_sample_state),
                                   time_major = True,
                                   dtype=tf.float32)

with tf.control_dependencies([tf.assign(sample_c[li],sample_state[li][0]) for li in range(n_layers)]+
                              [tf.assign(sample_h[li],sample_state[li][1]) for li in range(n_layers)]):  
  sample_prediction = tf.nn.xw_plus_b(tf.reshape(sample_outputs,[1,-1]), w, b)

print('\tAll done')

运行 LSTM

在这里，您将训练和预测几个时期的股票价格走势，并查看预测随着时间的推移是变得更好还是更差。您按照以下步骤操作。我不会共享代码，因为我会共享完整 Jupyter 笔记本的链接。

**在时间序列上定义一组起点 ( *

*test_points_seq*

) 来评估模型

*对于每个时期

**对于训练数据的完整序列长度

****展开一组

*num_unrollings*

批次*

***用展开的批次训练神经网络

**计算平均训练损失

**对于测试集中的每个起点

**通过迭代测试点之前找到的先前数据点来更新 LSTM 状态

*num_unrollings*

*n_predict_once*

使用之前的预测作为当前输入，连续对步骤进行预测*

**计算预测点与这些时间戳的真实股票价格之间的 MSE 损失

*n_predict_once*

可视化预测

您可以看到 MSE 损失如何随着训练量的增加而下降。这是一个好兆头，表明该模型正在学习一些有用的东西。为了量化您的发现，您可以将网络的 MSE 损失与进行标准平均 (0.004) 时获得的 MSE 损失进行比较。您可以看到 LSTM 的表现比标准平均要好。而且您知道标准平均法（尽管并不完美）合理地遵循了真实的股价走势。

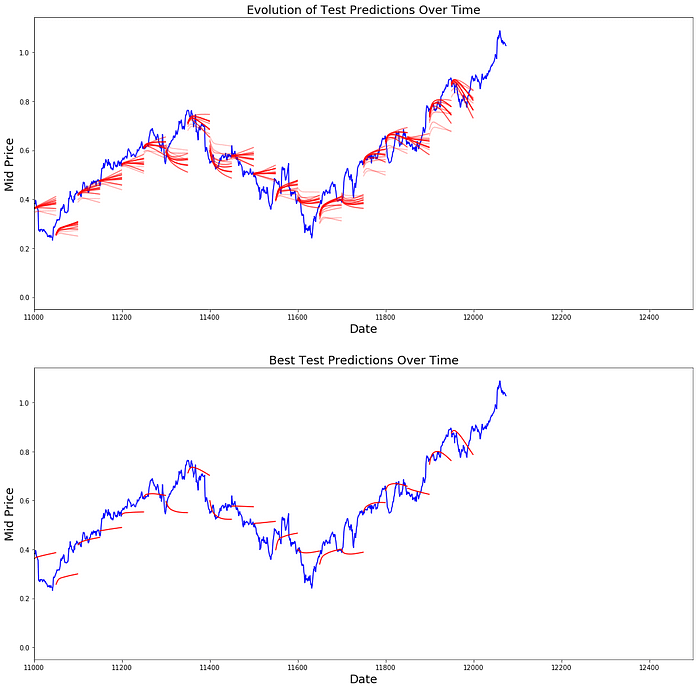
尽管并不完美，但 LSTM 似乎在大多数情况下都能正确预测股票价格行为。请注意，您的预测大致在 0 到 1.0 的范围内（即，不是真实的股票价格）。这没关系，因为您预测的是股票价格走势，而不是价格本身。

结论

我希望您觉得本教程有用。我应该指出，这对我来说是一次有益的经历。在本教程中，我了解到建立能够正确预测股票价格走势的模型是多么困难。您一开始就知道为什么需要对股票价格进行建模。接下来是下载数据的解释和代码。然后您了解了两种平均技术，可以让您对未来进行一步预测。接下来您会发现，当您需要预测未来的不止一步时，这些方法是徒劳的。此后，您讨论了如何使用 LSTM 来预测未来的许多步骤。最后，您将结果可视化，并发现您的模型（尽管并不完美）非常擅长正确预测股票价格走势。

在这里，我将阐述本教程的几个要点。

  1. 股票价格/走势预测是一项极其困难的任务。就我个人而言，我认为任何股票预测模型都不应该被视为理所当然并盲目依赖它们。然而，模型在大多数时候可能能够正确预测股价走势，但并非总是如此。
  2. 不要被那些显示预测曲线与真实股价完全重叠的文章所愚弄。这可以通过简单的平均技术来复制，但在实践中它是无用的。更明智的做法是预测股价走势。
  3. 模型的超参数对您获得的结果极其敏感。因此，一个非常好的做法是对超参数运行一些超参数优化技术（例如网格搜索/随机搜索）。这里我列出了一些最关键的超参数；优化器的学习率、层数和每层隐藏单元的数量、优化器（我发现 Adam 表现最好）、模型类型（GRU/LSTM/带窥视孔的 LSTM）
  4. 在本教程中，您做了一些错误的事情（由于数据量太小）！也就是说，您使用测试损失来降低学习率。这间接地将有关测试集的信息泄漏到训练过程中。处理此问题的更好方法是使用单独的验证集（除了测试集）并根据验证集的性能衰减学习率。
标签： 人工智能 lstm tensorflow
本文转载自: https://blog.csdn.net/xiaoshun007/article/details/135970384
版权归原作者 xiaoshun007～ 所有， 如有侵权，请联系我们删除。
登录后发布评论

“AI实战-Tensorflow使用 LSTM 进行股票市场预测 (完整步骤+源码讲解)”的评论:

还没有评论
关于作者
...
overfit同步小助手
文章同步
相关阅读

网吧业务安全对抗(有源码)

网络安全售前入门09安全服务——安全加固服务

安全测试理论

Edge：速度与安全的完美融合

解决win11/win10挂载网络盘映射网络驱动器报错找不到网络名0x80070043

一文教你在centos 7.9中安装mysql5.7(超级详细)

Windows和Linux中Langchain-chatchat0.3.1.3部署

文章导航