文章目录
创建与初始化
OpenCV中的矩阵操作非常重要,本文总结了矩阵的创建、初始化以及基本矩阵操作,给出了示例代码,主要内容包括:
1.1 数据类型
建立矩阵必须要指定矩阵存储的数据类型,图像处理中常用的几种数据类型如下:
CV_8UC1// 8位无符号单通道
CV_8UC3// 8位无符号3通道
CV_8UC4
CV_32FC1// 32位浮点型单通道
CV_32FC3// 32位浮点型3通道
CV_32FC4
包括数据位深度8位、32位,数据类型U:uchar、F:float型以及通道数C1:单通道、C3:三通道、C4:四通道。
1.2 基本方法
我们可以通过载入图像来创建Mat类型矩阵,当然也可以直接手动创建矩阵,基本方法是指定矩阵尺寸和数据类型:
// 基本方法
cv::Mat a(cv::Size(5,5),CV_8UC1);// 单通道
cv::Mat b = cv::Mat(cv::Size(5,5),CV_8UC3);//3通道每个矩阵元素包含3个uchar值
cout<<"a = "<<endl<<a<<endl<<endl;
cout<<"b = "<<endl<<b<<endl<<endl;system("pause");`
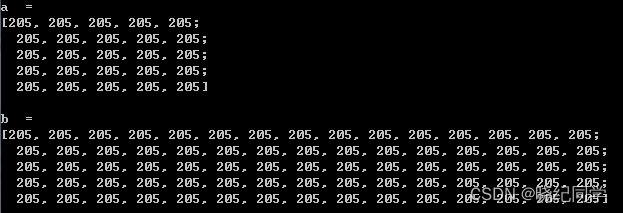
3通道矩阵中,一个矩阵元素包含3个变量。
1.3 初始化方法
上述方法不初始化矩阵数据,因此将出现随机值。如果想避免这种情况,可使用Mat类的几种初始化创建矩阵的方法:
// 初始化方法
cv::Mat mz = cv::Mat::zeros(cv::Size(5,5),CV_8UC1);// 全零矩阵
cv::Mat mo = cv::Mat::ones(cv::Size(5,5),CV_8UC1);// 全1矩阵
cv::Mat me = cv::Mat::eye(cv::Size(5,5),CV_32FC1);// 对角线为1的对角矩阵
cout<<"mz = "<<endl<<mz<<endl<<endl;
cout<<"mo = "<<endl<<mo<<endl<<endl;
cout<<"me = "<<endl<<me<<endl<<endl;
运行结果: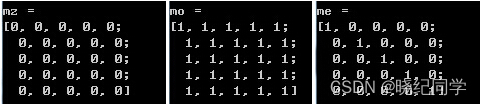
矩阵加减法
我们可以使用"+“和”-"符号进行矩阵加减运算。
cv::Mat a=Mat::eye(Size(3,2), CV_32F);
cv::Mat b=Mat::ones(Size(3,2), CV_32F);
cv::Mat c= a+b;
cv::Mat d= a-b;
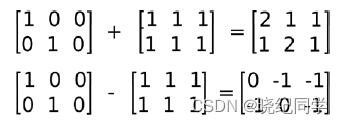
矩阵乘法
使用"*"号计算矩阵与标量相乘,矩阵与矩阵相乘(必须满足矩阵相乘的行列数对应规则)
Mat m1=Mat::eye(2,3, CV_32F);//使用cv命名空间可省略cv::前缀,下同
Mat m2=Mat::ones(3,2, CV_32F);
cout<<"m1 = "<<endl<<m1<<endl<<endl;
cout<<"m2 = "<<endl<<m2<<endl<<endl;// Scalar by matrix
cout <<"\nm1.*2 = \n"<< m1*2<< endl;// matrix per element multiplication
cout <<"\n(m1+2).*(m1+3) = \n"<<(m1+1).mul(m1+3)<< endl;// Matrix multiplication
cout <<"\nm1*m2 = \n"<< m1*m2 << endl;

矩阵转置
矩阵转置是将矩阵的行与列顺序对调(第i行转变为第i列)形成一个新的矩阵。OpenCV通过Mat类的t()函数实现。
// 转置
Mat m1=Mat::eye(2,3, CV_32F);
Mat m1t = m1.t();
cout<<"m1 = "<<endl<<m1<<endl<<endl;
cout<<"m1t = "<<endl<<m1t<<endl<<endl;system("pause");
运行结果: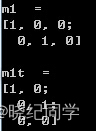
矩阵求逆
逆矩阵在某些算法中经常出现,在OpenCV中通过Mat类的inv()方法实现
// 求逆
Mat meinv = me.inv();
cout<<"me = "<<endl<<me<<endl<<endl;
cout<<"meinv = "<<endl<<meinv<<endl<<endl;system("pause");
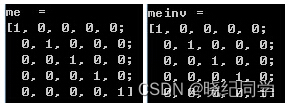
单位矩阵的逆就是其本身。
矩阵非零元素个数
计算物体的像素或面积常需要用到计算矩阵中的非零元素个数,OpenCV中使用countNonZero()函数实现。
// 非零元素个数
int nonZerosNum = countNonZero(me); // me为输入矩阵或图像
cout<<"me = "<<endl<<me<<endl;
cout<<"me中非零元素个数 = "<<nonZerosNum<<endl<<endl;
system(“pause”);
运行结果: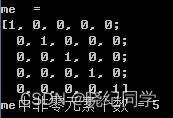
矩阵均值与标准差
OpenCV提供了矩阵均值和标准差计算功能,可以使用meanStdDev(src,mean,stddev)函数实现
参数
src – 输入矩阵或图像
mean – 均值,OutputArray
stddev – 标准差,OutputArray
// 均值方差
Mat mean;
Mat stddev;meanStdDev(me, mean, stddev);//me为前文定义的5×5对角阵
cout<<"mean = "<<mean<<endl;
cout<<"stddev = "<<stddev<<endl;system("pause");

需要说明的是,如果src是多通道图像或多维矩阵,则函数分别计算不同通道的均值与标准差,因此返回值mean和stddev为对应维度的向量。
Mat mean3;
Mat stddev3;
Mat m3(cv::Size(5,5),CV_8UC3,Scalar(255,200,100));
cout<<"m3 = "<<endl<<m3<<endl<<endl;meanStdDev(m3, mean3, stddev3);
cout<<"mean3 = "<<mean3<<endl;
cout<<"stddev3 = "<<stddev3<<endl;system("pause");
多通道矩阵运算结果:
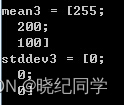
矩阵全局极值及位置
求输入矩阵的全局最大最小值及其位置,可使用函数:
voidminMaxLoc(InputArray src, CV_OUT double* minVal,
CV_OUT double* maxVal=0, CV_OUT Point* minLoc=0,
CV_OUT Point* maxLoc=0, InputArray mask=noArray());
参数:
src – 输入单通道矩阵(图像).
minVal – 指向最小值的指针, 如果未指定则使用NULL
maxVal – 指向最大值的指针, 如果未指定则使用NULL
minLoc – 指向最小值位置(2维情况)的指针, 如果未指定则使用NULL
maxLoc – 指向最大值位置(2维情况)的指针, 如果未指定则使用NULL
mask – 可选的蒙版,用于选择待处理子区域
// 求极值 最大、最小值及其位置
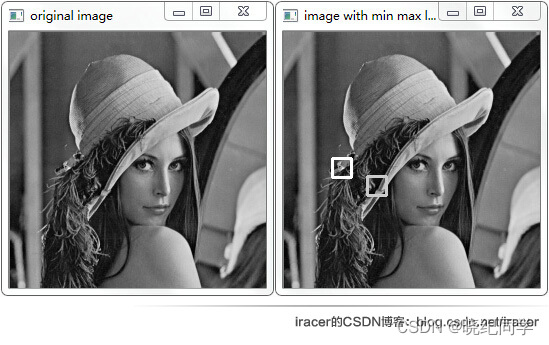
Mat img =imread("Lena.jpg",0);imshow("original image",img);double minVal=0,maxVal=0;
cv::Point minPt, maxPt;minMaxLoc(img,&minVal,&maxVal,&minPt,&maxPt);
cout<<"min value = "<<minVal<<endl;
cout<<"max value = "<<maxVal<<endl;
cout<<"minPt = ("<<minPt.x<<","<<minPt.y<<")"<<endl;
cout<<"maxPt = ("<<maxPt.x<<","<<maxPt.y<<")"<<endl;
cout<<endl;
cv::Rect rectMin(minPt.x-10,minPt.y-10,20,20);
cv::Rect rectMax(maxPt.x-10,maxPt.y-10,20,20);
cv::rectangle(img,rectMin,cv::Scalar(200),2);
cv::rectangle(img,rectMax,cv::Scalar(255),2);imshow("image with min max location",img);
cv::waitKey();
运行结果: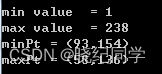
GEMM 通用矩阵乘法
void cvGEMM( const CvArr* src1, const CvArr* src2, double alpha,
const CvArr* src3, double beta, CvArr* dst, int tABC=0 );
#define cvMatMulAdd( src1, src2, src3, dst ) cvGEMM( src1, src2, 1, src3, 1, dst, 0 )
#define cvMatMul( src1, src2, dst ) cvMatMulAdd( src1, src2, 0, dst )
src1
第一输入数组
src2
第二输入数组
src3
第三输入数组 (偏移量),如果没有偏移量,可以为空( NULL) 。
dst
输出数组
tABC
T操作标志,可以是 0 或者下面列举的值的组合:
CV_GEMM_A_T - 转置 src1
CV_GEMM_B_T - 转置 src2
CV_GEMM_C_T - 转置 src3
例如, CV_GEMM_A_T+CV_GEMM_C_T 对应
alphasrc1Tsrc2 + beta*src3T
函数 cvGEMM 执行通用矩阵乘法:
dst = alpha*op(src1)op(src2) + betaop(src3), 这里 op(X) 是 X 或者 XT
所有的矩阵应该有相同的数据类型和协调的矩阵大小。支持实数浮点矩阵或者复数浮点矩阵。
Transform 对数组每一个元素执行矩阵变换
void cvTransform( const CvArr* src, CvArr* dst, const CvMat* transmat, const CvMat* shiftvec=NULL );
src
输入数组
dst
输出数组
transmat
变换矩阵
shiftvec
可选偏移向量
函数 cvTransform 对数组 src 每一个元素执行矩阵变换并将结果存储到 dst:
dst(I)=transmat*src(I) + shiftvec
或者
dst(I)k=sumj(transmat(k,j)*src(I)j) + shiftvec(k)
N-通道数组 src 的每一个元素都被视为一个N元向量,使用一个 M×N 的变换矩阵 transmat 和偏移向量 shiftvec 把它变换到一个 M-通道的数组 dst 的一个元素中。 这里可以选择将偏移向量 shiftvec 嵌入到 transmat 中。这样的话 transmat 应该是 M×N+1 的矩阵,并且最右边的一列被看作是偏移向量 。
输入数组和输出数组应该有相同的位深(depth)和同样的大小或者 ROI 大小。 transmat 和 shiftvec 应该是实数浮点矩阵。
该函数可以用来进行 ND 点集的几何变换,任意的线性颜色空间变换,通道转换等。
MulTransposed 计算数组和数组的转置的乘积
void cvMulTransposed( const CvArr* src, CvArr* dst, int order, const CvArr* delta=NULL );
src
输入矩阵
dst
目标矩阵
order
乘法顺序
delta
一个可选数组, 在乘法之前从 src 中减去该数组。
函数 cvMulTransposed 计算 src 和它的转置的乘积。
函数求值公式:
如果 order=0
dst=(src-delta)*(src-delta)T
否则
dst=(src-delta)T*(src-delta)
Trace 返回矩阵的迹
CvScalar cvTrace( const CvArr* mat );
mat
输入矩阵
函数 cvTrace 返回矩阵mat的对角线元素的和。
tr(src) = ∑ mat(i,i)
i
Transpose 矩阵的转置
void cvTranspose( const CvArr* src, CvArr* dst );
#define cvT cvTranspose
src
输入矩阵
dst
目标矩阵
函数 cvTranspose 对矩阵 src 求转置:
dst(i,j)=src(j,i)
注意,假设是复数矩阵不会求得复数的共轭。共轭应该是独立的:查看的 cvXorS 例子代码。
Det 返回矩阵的行列式值
double cvDet( const CvArr* mat );
mat
输入矩阵
函数 cvDet 返回方阵 mat 的行列式值。对小矩阵直接计算,对大矩阵用 高斯(GAUSSIAN)消去法。对于对称正定(positive-determined)矩阵也可以用 SVD 函数来求,U=V=NULL ,然后用 w 的对角线元素的乘积来计算行列式。
Invert 查找矩阵的逆矩阵或伪逆矩阵
double cvInvert( const CvArr* src, CvArr* dst, int method=CV_LU );
#define cvInv cvInvert
src
输入矩阵
dst
目标矩阵
method
求逆方法:
CV_LU -最佳主元选取的高斯消除法
CV_SVD - 奇异值分解法 (SVD)
CV_SVD_SYM - 正定对称矩阵的 SVD 方法
函数 cvInvert 对矩阵 src 求逆并将结果存储到 dst。
如果是 LU 方法该函数返回 src 的行列式值 (src 必须是方阵)。 如果是 0, 矩阵不求逆, dst 用 0 填充。
如果 SVD 方法该函数返回 src 的条件数的倒数(最小奇异值和最大奇异值的比值) ,如果 src 全为 0 则返回0。 如果 src 是奇异的, SVD 方法计算一个伪逆矩阵。
Solve 求解线性系统或者最小二乘法问题
int cvSolve( const CvArr* src1, const CvArr* src2, CvArr* dst, int method=CV_LU );
src1 输入矩阵
src2 线性系统的右部
dst 输出解答 method
解决方法(矩阵求逆) :
CV_LU - 最佳主元选取的高斯消除法
CV_SVD - 奇异值分解法 (SVD)
CV_SVD_SYM - 对正定对称矩阵的 SVD 方法
函数 cvSolve 解决线性系统或者最小二乘法问题 (后者用 SVD 方法可以解决):
/mbox{dst} = /arg /min_X |/mbox{src1}/cdot X-/mbox{src2}|
如果使用 CV_LU 方法。 如果 src1 是非奇异的,该函数则返回 1 ,否则返回 0 ,在后一种情况下 dst 是无效的。
SVD 对实数浮点矩阵进行奇异值分解
void cvSVD( CvArr* A, CvArr* W, CvArr* U=NULL, CvArr* V=NULL, int flags=0 );
A M×N 的输入矩阵 W 结果奇异值矩阵 (M×N 或者 N×N) 或者 向量 (N×1). U 可选的左部正交矩阵 (M×M or
M×N). 如果 CV_SVD_U_T 被指定, 应该交换上面所说的行与列的数目。 V 可选右部正交矩阵(N×N)
flags
操作标志; 可以是 0 或者下面的值的组合:
CV_SVD_MODIFY_A 通过操作可以修改矩阵 src1 。这样处理速度会比较快。
CV_SVD_U_T 意味着会返回转置矩阵 U ,指定这个标志将加快处理速度。
CV_SVD_V_T 意味着会返回转置矩阵 V ,指定这个标志将加快处理速度。
函数 cvSVD 将矩阵 A 分解成一个对角线矩阵和两个正交矩阵的乘积:
/mathbf{/it A=U W V^T}
这里 W 是一个奇异值的对角线矩阵,它可以被编码成奇异值的一维向量,U 和 V 也是一样。 所有的奇异值都是非负的并按降序存储。(U 和 V
也相应的存储)。SVD 算法在数值处理上已经很稳定,它的典型应用包括:
当 A 是一个方阵、对称阵和正矩阵时精确的求解特征值问题,例如, 当 A 时一个协方差矩阵时。在这种情况下 W 将是一个特征值的的向量,并且
U=V是矩阵的特征向量(因此,当需要计算特征向量时 U 和 V 只需要计算其中一个就可以了) 。 精确的求解病态线性系统。
超定线性系统的最小二乘求解。上一个问题和这个问题都可以用指定 CV_SVD 的 cvSolve 方法。
精确计算矩阵的不同特征,如秩(非零奇异值的数目), 条件数(最大奇异值和最小奇异值的比例),
行列式值(行列式的绝对值等于奇异值的乘积).上述的所有这些值都不要求计算矩阵 U 和 V 。
SVBkSb 奇异值回代算法(back substitution)
void cvSVBkSb( const CvArr* W, const CvArr* U, const CvArr* V,
const CvArr* B, CvArr* X, int flags );
W
奇异值矩阵或者向量
U
左正交矩阵 (可能是转置的)
V
右正交矩阵 (可能是转置的)
B
原始矩阵 A 的伪逆的乘法矩阵。这个是可选参数。如果它被省略则假定它是一个适当大小的单位矩阵(因此 x 将是 A 的伪逆的重建).。
X
目标矩阵: 奇异值回代算法的结果
flags
操作标志, 和刚刚讨论的 cvSVD 的标志一样。
函数 cvSVBkSb 为被分解的矩阵 A 和矩阵 B 计算回代逆(back substitution) (参见 cvSVD 说明) :
X=VW-1UT*B
这里
W-1(i,i)=1/W(i,i) 如果 W(i,i) > epsilon•sumiW(i,i),
否则:0.
epsilon 是一个依赖于矩阵数据类型的的很小的数。该函数和 cvSVD 函数被用来执行 cvInvert 和 cvSolve, 用这些函数 (svd & bksb)的原因是初级函数(low-level) 函数可以避免高级函数 (inv & solve) 计算中内部分配的临时矩阵。
EigenVV 计算对称矩阵的特征值和特征向量
void cvEigenVV( CvArr* mat, CvArr* evects, CvArr* evals, double eps=0 );
mat
输入对称方阵。在处理过程中将被改变。
evects
特征向量输出矩阵, 连续按行存储
evals
特征值输出矩阵,按降序存储(当然特征值和特征向量的排序是同步的)。
eps
对角化的精确度 (典型地, DBL_EPSILON=≈10-15 就足够了)。
函数 cvEigenVV 计算矩阵 A 的特征值和特征向量:
mat*evects(i,:)’ = evals(i)*evects(i,:)’ (在 MATLAB 的记法)
矩阵 A 的数据将会被这个函数修改。
目前这个函数比函数 cvSVD 要慢,精确度要低, 如果已知 A 是正定的,(例如, 它是一个协方差矩阵), 它通常被交给函数 cvSVD 来计算其特征值和特征向量,尤其是在不需要计算特征向量的情况下
CalcCovarMatrix 计算向量集合的协方差矩阵
void cvCalcCovarMatrix( const CvArr** vects, int count, CvArr* cov_mat, CvArr* avg, int flags );
vects
输入向量。他们必须有同样的数据类型和大小。这个向量不一定非是一维的,他们也可以是二维(例如,图像)等等。
count
输入向量的数目
cov_mat
输出协方差矩阵,它是浮点型的方阵。
avg
输入或者输出数组 (依赖于标记“flags”) - 输入向量的平均向量。
flags
操作标志,下面值的组合:
CV_COVAR_SCRAMBLED - 输出协方差矩阵按下面计算:
scale * [vects[0] − avg,vects[1] − avg,…]T * [vects[0] − avg,vects[1] − avg,…], 即协方差矩阵是 count×count. 这样一个不寻常的矩阵用于一组大型向量的快速PCA方法(例如, 人脸识别的 EigenFaces 技术)。这个混杂(“scrambled”)矩阵的特征值将和真正的协方差矩阵的特征值匹配,真正的特征向量可以很容易的从混杂 (“scrambled”)协方差矩阵的特征向量中计算出来。
CV_COVAR_NORMAL - 输出协方差矩阵被计算成:
scale * [vects[0] − avg,vects[1] − avg,…] * [vects[0] − avg,vects[1] − avg,…]T, 也就是说, cov_mat 将是一个和每一个输入向量的元素数目具有同样线性大小的通常协方差矩阵。 CV_COVAR_SCRAMBLED 和 CV_COVAR_NORMAL 只能同时指定其中一个。
CV_COVAR_USE_AVG - 如果这个标志被指定, 该函数将不会从输入向量中计算 avg ,而是用过去的 avg 向量,如果 avg 已经以某种方式计算出来了这样做是很有用的。或者如果协方差矩阵是部分计算出来的 - 倘若这样, avg 不是输入向量的子集的平均值,而是整个集合的平均向量。
CV_COVAR_SCALE - 如果这个标志被指定,协方差矩阵被缩放了。 the covariation matrix is scaled.在 “normal” 模式下缩放比例是 1./count, 在 “scrambled” 模式下缩放比例是每一个输入向量的元素总和的倒数。 缺省地(如果没有指定标志) 协方差矩阵不被缩放 (scale=1)。
函数 cvCalcCovarMatrix 计算输入向量的协方差矩阵和平均向量。该函数 可以被运用到主成分分析中(PCA),以及马氏距离(Mahalanobis distance)比较向量中等等。
Mahalanobis 计算两个向量之间的马氏距离(Mahalanobis distance)
double cvMahalanobis( const CvArr* vec1, const CvArr* vec2, CvArr* mat );
vec1
第一个一维输入向量
vec2
第二个一维输入向量
mat
协方差矩阵的逆矩阵
函数 cvMahalanobis 计算两个向量之间的加权距离,其返回结果是:
d(vec1,vec2)=/sqrt{ /sum_{i,j} /{mat(i,j)(vec1(i)-vec2(i))(vec1(j)-vec2(j))/} }
协方差矩阵可以用函数cvCalcCovarMatrix 计算出来,逆矩阵可以用函数 cvInvert 计算出来 (CV_SVD 方法是一个比较好的选择, 因为矩阵可能是奇异的).
CalcPCA 对一个向量集做PCA变换
void cvCalcPCA( const CvArr* data, CvArr* avg,
CvArr* eigenvalues, CvArr* eigenvectors, int flags );
data
输入数据,每个向量是单行向量(CV_PCA_DATA_AS_ROW)或者单列向量(CV_PCA_DATA_AS_COL).
avg
平均向量,在函数内部计算或者由调用者提供
eigenvalues
输出的协方差矩阵的特征值
eigenvectors
输出的协方差矩阵的特征向量(也就是主分量),每个向量一行
flags
操作标志,可以是以下几种方式的组合:
CV_PCA_DATA_AS_ROW - 向量以行的方式存放(也就是说任何一个向量都是连续存放的)
CV_PCA_DATA_AS_COL - 向量以列的方式存放(也就是说某一个向量成分的数值是连续存放的)
(上面两种标志是互相排斥的)
CV_PCA_USE_AVG - 使用预先计算好的平均值
该函数对某个向量集做PCA变换.它首先利用cvCalcCovarMatrix计算协方差矩阵然后计算协方差矩阵的特征值与特征向量.输出的特征值/特征向量的个数小于或者等于MIN(rows(data),cols(data)).
ProjectPCA 把向量向某个子空间投影
void cvProjectPCA( const CvArr* data, const CvArr* avg,
const CvArr* eigenvectors, CvArr* result )
data
输入数据,每个向量可以是单行或者单列
avg
平均向量.要么它是单行向量那么意味着输入数据以行数据的形式存放,要么就是单列向量,那么就意味着那么输入向量就是以列的方式存放.
eigenvectors
特征向量(主分量),每个向量一行.
result
输出的分解系数矩阵,矩阵的行数必须与输入向量的个数相等,矩阵的列数必须小于特征向量的行数.
该函数将输入向量向一个正交系(eigenvectors)投影.在计算点乘之前,输入向量要减去平均向量:
result(i,:)=(data(i,:)-avg)*eigenvectors’ // for CV_PCA_DATA_AS_ROW layout.
[ 编辑]
BackProjectPCA
根据投影系数重构原来的向量
void cvBackProjectPCA( const CvArr* proj, const CvArr* avg,
const CvArr* eigenvects, CvArr* result );
proj
输入数据,与cvProjectPCA里面的格式一致
avg
平均向量.如果它是单行向量,那么意味着输出向量是以行的方式存放.否则就是单列向量,那么输出向量就是以列的方式存放.
eigenvectors
特征向量(主分量),每个向量一行.
result
输出的重构出来的矩阵
该函数根据投影系数重构原来的向量:
result(i,:)=proj(i,:)*eigenvectors + avg // for CV_PCA_DATA_AS_ROW layout
附
矩阵操作
分配释放矩阵空间
综述:
OpenCV有针对矩阵操作的C语言函数. 许多其他方法提供了更加方便的C++接口,其效率与OpenCV一样.
OpenCV将向量作为1维矩阵处理.
矩阵按行存储,每行有4字节的校整.
分配矩阵空间:
CvMat* cvCreateMat(int rows, int cols, int type);
type: 矩阵元素类型. 格式为CV_<bit_depth>(S|U|F)C<number_of_channels>.
例如: CV_8UC1 表示8位无符号单通道矩阵, CV_32SC2表示32位有符号双通道矩阵.
例程:
CvMat* M = cvCreateMat(4,4,CV_32FC1);
释放矩阵空间:
CvMat* M = cvCreateMat(4,4,CV_32FC1);
cvReleaseMat(&M);
复制矩阵:
CvMat* M1 = cvCreateMat(4,4,CV_32FC1);
CvMat* M2;
M2=cvCloneMat(M1);
初始化矩阵:
double a[] = { 1, 2, 3, 4,
5, 6, 7, 8,
9, 10, 11, 12 };
CvMat Ma=cvMat(3, 4, CV_64FC1, a);
另一种方法:
CvMat Ma;
cvInitMatHeader(&Ma, 3, 4, CV_64FC1, a);
初始化矩阵为单位阵:
CvMat* M = cvCreateMat(4,4,CV_32FC1);
cvSetIdentity(M); // 这里似乎有问题,不成功
存取矩阵元素
假设需要存取一个2维浮点矩阵的第(i,j)个元素.
间接存取矩阵元素:
cvmSet(M,i,j,2.0); // Set M(i,j)
t = cvmGet(M,i,j); // Get M(i,j)
直接存取,假设使用4-字节校正:
CvMat* M = cvCreateMat(4,4,CV_32FC1);
int n = M->cols;
float *data = M->data.fl;
data[i*n+j] = 3.0;
直接存取,校正字节任意:
CvMat* M = cvCreateMat(4,4,CV_32FC1);
int step = M->step/sizeof(float);
float *data = M->data.fl;
(data+i*step)[j] = 3.0;
直接存取一个初始化的矩阵元素:
double a[16];
CvMat Ma = cvMat(3, 4, CV_64FC1, a);
a[i*4+j] = 2.0; // Ma(i,j)=2.0;
矩阵/向量操作
矩阵-矩阵操作:
CvMat *Ma, *Mb, Mc;
cvAdd(Ma, Mb, Mc); // Ma+Mb -> Mc
cvSub(Ma, Mb, Mc); // Ma-Mb -> Mc
cvMatMul(Ma, Mb, Mc); // MaMb -> Mc
按元素的矩阵操作:
CvMat *Ma, *Mb, *Mc;
cvMul(Ma, Mb, Mc); // Ma.*Mb -> Mc
cvDiv(Ma, Mb, Mc); // Ma./Mb -> Mc
cvAddS(Ma, cvScalar(-10.0), Mc); // Ma.-10 -> Mc
向量乘积:
double va[] = {1, 2, 3};
double vb[] = {0, 0, 1};
double vc[3];
CvMat Va=cvMat(3, 1, CV_64FC1, va);
CvMat Vb=cvMat(3, 1, CV_64FC1, vb);
CvMat Vc=cvMat(3, 1, CV_64FC1, vc);
double res=cvDotProduct(&Va,&Vb); // 点乘: Va . Vb -> res
cvCrossProduct(&Va, &Vb, &Vc); // 向量积: Va x Vb -> Vc
end{verbatim}
注意 Va, Vb, Vc 在向量积中向量元素个数须相同.
单矩阵操作:
CvMat *Ma, *Mb;
cvTranspose(Ma, Mb); // transpose(Ma) -> Mb (不能对自身进行转置)
CvScalar t = cvTrace(Ma); // trace(Ma) -> t.val[0]
double d = cvDet(Ma); // det(Ma) -> d
cvInvert(Ma, Mb); // inv(Ma) -> Mb
非齐次线性系统求解:
CvMat* A = cvCreateMat(3,3,CV_32FC1);
CvMat* x = cvCreateMat(3,1,CV_32FC1);
CvMat* b = cvCreateMat(3,1,CV_32FC1);
cvSolve(&A, &b, &x); // solve (Ax=b) for x
特征值分析(针对对称矩阵):
CvMat* A = cvCreateMat(3,3,CV_32FC1);
CvMat* E = cvCreateMat(3,3,CV_32FC1);
CvMat* l = cvCreateMat(3,1,CV_32FC1);
cvEigenVV(&A, &E, &l); // l = A的特征值 (降序排列)
// E = 对应的特征向量 (每行)
奇异值分解SVD:
CvMat* A = cvCreateMat(3,3,CV_32FC1);
CvMat* U = cvCreateMat(3,3,CV_32FC1);
CvMat* D = cvCreateMat(3,3,CV_32FC1);
CvMat* V = cvCreateMat(3,3,CV_32FC1);
cvSVD(A, D, U, V, CV_SVD_U_T|CV_SVD_V_T); // A = U D V^T
标号使得 U 和 V 返回时被转置(若没有转置标号,则有问题不成功!!!).
视频序列操作
从视频序列中抓取一帧
OpenCV支持从摄像头或视频文件(AVI)中抓取图像.
从摄像头获取初始化:
CvCapture* capture = cvCaptureFromCAM(0); // capture from video device #0
从视频文件获取初始化:
CvCapture* capture = cvCaptureFromAVI(“infile.avi”);
抓取帧:
IplImage* img = 0;
if(!cvGrabFrame(capture)){ // 抓取一帧
printf(“Could not grab a frame/n/7”);
exit(0);
}
img=cvRetrieveFrame(capture); // 恢复获取的帧图像
要从多个摄像头同时获取图像, 首先从每个摄像头抓取一帧. 在抓取动作都结束后再恢复帧图像.
释放抓取源:
cvReleaseCapture(&capture);
注意由设备抓取的图像是由capture函数自动分配和释放的. 不要试图自己释放它.
获取/设定帧信息
获取设备特性:
cvQueryFrame(capture); // this call is necessary to get correct
// capture properties
int frameH = (int) cvGetCaptureProperty(capture, CV_CAP_PROP_FRAME_HEIGHT);
int frameW = (int) cvGetCaptureProperty(capture, CV_CAP_PROP_FRAME_WIDTH);
int fps = (int) cvGetCaptureProperty(capture, CV_CAP_PROP_FPS);
int numFrames = (int) cvGetCaptureProperty(capture, CV_CAP_PROP_FRAME_COUNT);
所有帧数似乎只与视频文件有关. 用摄像头时不对,奇怪!!!.
获取帧信息:
float posMsec = cvGetCaptureProperty(capture, CV_CAP_PROP_POS_MSEC);
int posFrames = (int) cvGetCaptureProperty(capture, CV_CAP_PROP_POS_FRAMES);
float posRatio = cvGetCaptureProperty(capture, CV_CAP_PROP_POS_AVI_RATIO);
获取所抓取帧在视频序列中的位置, 从首帧开始按[毫秒]算. 或者从首帧开始从0标号, 获取所抓取帧的标号. 或者取相对位置,首帧为0,末帧为1, 只对视频文件有效.
设定所抓取的第一帧标号:
// 从视频文件相对位置0.9处开始抓取
cvSetCaptureProperty(capture, CV_CAP_PROP_POS_AVI_RATIO, (double)0.9);
只对从视频文件抓取有效. 不过似乎也不成功!!!
存储视频文件
初始化视频存储器:
CvVideoWriter *writer = 0;
int isColor = 1;
int fps = 25; // or 30
int frameW = 640; // 744 for firewire cameras
int frameH = 480; // 480 for firewire cameras
writer=cvCreateVideoWriter(“out.avi”,CV_FOURCC(‘P’,‘I’,‘M’,‘1’),
fps,cvSize(frameW,frameH),isColor);
其他有效编码:
CV_FOURCC(‘P’,‘I’,‘M’,‘1’) = MPEG-1 codec
CV_FOURCC(‘M’,‘J’,‘P’,‘G’) = motion-jpeg codec (does not work well)
CV_FOURCC(‘M’, ‘P’, ‘4’, ‘2’) = MPEG-4.2 codec
CV_FOURCC(‘D’, ‘I’, ‘V’, ‘3’) = MPEG-4.3 codec
CV_FOURCC(‘D’, ‘I’, ‘V’, ‘X’) = MPEG-4 codec
CV_FOURCC(‘U’, ‘2’, ‘6’, ‘3’) = H263 codec
CV_FOURCC(‘I’, ‘2’, ‘6’, ‘3’) = H263I codec
CV_FOURCC(‘F’, ‘L’, ‘V’, ‘1’) = FLV1 codec
若把视频编码设为-1则将打开一个编码选择窗口(windows系统下).
存储视频文件:
IplImage* img = 0;
int nFrames = 50;
for(i=0;i<nFrames;i++){
cvGrabFrame(capture); // 抓取帧
img=cvRetrieveFrame(capture); // 恢复图像
cvWriteFrame(writer,img); // 将帧添加入视频文件
}
若想在抓取中查看抓取图像, 可在循环中加入下列代码:
cvShowImage(“mainWin”, img);
key=cvWaitKey(20); // wait 20 ms
若没有20[毫秒]延迟,将无法正确显示视频序列.
释放视频存储器:
cvReleaseVideoWriter(&writer);
其他矩阵运算函数列表
add
矩阵加法,A+B的更高级形式,支持mask
scaleAdd
矩阵加法,一个带有缩放因子dst(I)= scale *src1(I)+src2(I)
addWeighted
矩阵加法,两个带有缩放因子dst(I)=saturate(src1(I)* alpha +src2(I)* beta + gamma)
subtract
矩阵减法,A-B的更高级形式,支持mask
multiply
矩阵逐元素乘法,同Mat::mul()函数,与A*B区别,支持mask
gemm
一个广义的矩阵乘法操作
divide
矩阵逐元素除法,与A/B区别,支持mask
abs
对每个元素求绝对值
absdiff
两个矩阵的差的绝对值
exp
求每个矩阵元素 src(I) 的自然数 e 的 src(I) 次幂 dst[I]=esrc(I)
pow
求每个矩阵元素 src(I) 的 p 次幂 dst[I]=src(I)p
log
求每个矩阵元素的自然数底 dst[I]= log|src(I)|(if src !=0)
sqrt
求每个矩阵元素的平方根
min, max
求每个元素的最小值或最大值返回这个矩阵 dst(I)=min(src1(I),src2(I)), max同
minMaxLoc
定位矩阵中最小值、最大值的位置
compare
返回逐个元素比较结果的矩阵
bitwise_and, bitwise_not, bitwise_or, bitwise_xor
每个元素进行位运算,分别是和、非、或、异或
cvarrToMat
旧版数据CvMat,IplImage,CvMatND转换到新版数据Mat
extractImageCOI
从旧版数据中提取指定的通道矩阵给新版数据Mat
randu
以Uniform分布产生随机数填充矩阵,同 RNG::fill(mat, RNG::UNIFORM)
randn
以Normal分布产生随机数填充矩阵,同 RNG::fill(mat, RNG::NORMAL)
randShuffle
随机打乱一个一维向量的元素顺序
theRNG()
返回一个默认构造的RNG类的对象
theRNG()::fill(...)
reduce
矩阵缩成向量
repeat
矩阵拷贝的时候指定按x/y方向重复
split
多通道矩阵分解成多个单通道矩阵
merge
多个单通道矩阵合成一个多通道矩阵
mixChannels
矩阵间通道拷贝,如Rgba[]到Rgb[]和Alpha[]
sort, sortIdx
为矩阵的每行或每列元素排序
setIdentity
设置单元矩阵
completeSymm
矩阵上下三角拷贝
inRange
检查元素的取值范围是否在另两个矩阵的元素取值之间,返回验证矩阵
checkRange
检查矩阵的每个元素的取值是否在最小值与最大值之间,返回验证结果bool
sum
求矩阵的元素和
mean
求均值
meanStdDev
均值和标准差
countNonZero
统计非零值个数
cartToPolar, polarToCart
笛卡尔坐标与极坐标之间的转换
flip
矩阵翻转
transpose
矩阵转置,比较 Mat::t() AT
trace
矩阵的迹
determinant
行列式 |A|,det(A)
eigen
矩阵的特征值和特征向量
invert
矩阵的逆或者伪逆,比较 Mat::inv()
magnitude
向量长度计算 dst(I)=sqrt(x(I)2+y(I)2)
Mahalanobis
Mahalanobis距离计算
phase
相位计算,即两个向量之间的夹角
norm
求范数,1-范数、2-范数、无穷范数
normalize
标准化
mulTransposed
矩阵和它自己的转置相乘 AT * A, dst =scale(src - delta)T(src - delta)
convertScaleAbs
先缩放元素再取绝对值,最后转换格式为8bit型
calcCovarMatrix
计算协方差阵
solve
求解1个或多个线性系统或者求解最小平方问题(least-squares problem)
solveCubic
求解三次方程的根
solvePoly
求解多项式的实根和重根
dct, idct
正、逆离散余弦变换,idct同dct(src, dst, flags | DCT_INVERSE)
dft, idft
正、逆离散傅立叶变换, idft同dft(src, dst, flags | DTF_INVERSE)
LUT
查表变换
getOptimalDFTSize
返回一个优化过的DFT大小
mulSpecturms
两个傅立叶频谱间逐元素的乘法
上表引自:http://blog.sina.com.cn/s/blog_7908e1290101i97z.html
转载请注明出处(本文更新链接):http://blog.csdn.net/iracer/article/details/51296631
版权归原作者 晓纪同学 所有, 如有侵权,请联系我们删除。