引言
本着“凡我不能创造的,我就不能理解”的思想,本系列文章会基于纯Python以及NumPy从零创建自己的深度学习框架,该框架类似PyTorch能实现自动求导。
要深入理解深度学习,从零开始创建的经验非常重要,从自己可以理解的角度出发,尽量不使用外部完备的框架前提下,实现我们想要的模型。本系列文章的宗旨就是通过这样的过程,让大家切实掌握深度学习底层实现,而不是仅做一个调包侠。
本系列文章首发于微信公众号:JavaNLP
我们已经了解了线性回归和逻辑回归,本文来学习深度学习中神经网络的基础构建——神经元,以及常见的激活函数。
神经元
神经网络和逻辑回归很像,但神经网络更强大。而神经网络是由很多个神经元(Neuron)组成的。一个神经元将实数集作为输入,然后应用某种运算,产生一个实数输出。
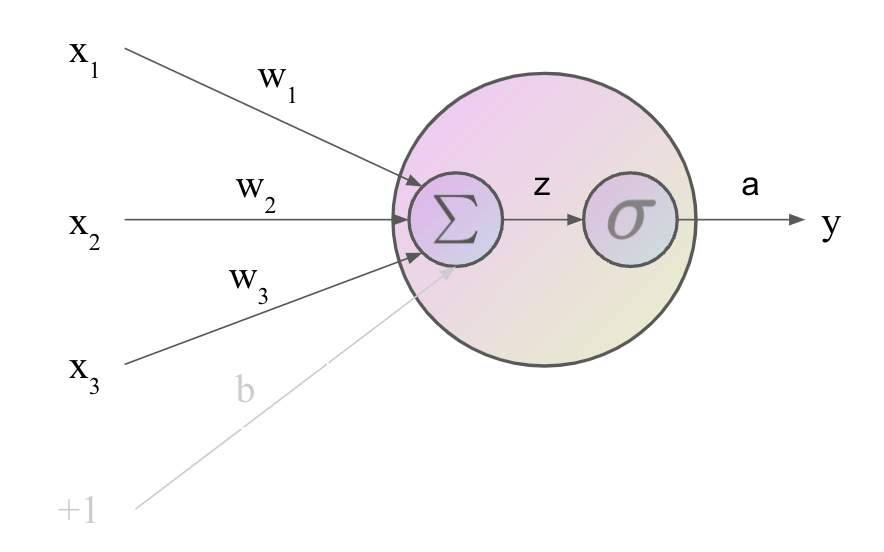
在神经元内部,如上图所示,神经元首先计算输入的加权和
∑
i
w
i
x
i
\sum_i w_i x_i
∑iwixi,然后加上偏置项
b
b
b。给定输入
x
1
,
⋯
,
x
n
x_1,\cdots,x_n
x1,⋯,xn,每个输入对应一个权重,得到加权和
z
z
z:
z
=
b
+
∑
i
w
i
x
i
(1)
z = b + \sum_i w_i x_i \tag 1
z=b+i∑wixi(1)
通常使用向量的形式描述更加方便。这样
z
z
z由向量
w
w
w和标量
b
b
b,以及输入向量
x
x
x来描述:
z
=
w
⋅
x
+
b
(2)
z =w \cdot x +b \tag 2
z=w⋅x+b(2)
注意这里得到的
z
z
z只是一个实数(标量)。
最后,我们不是直接使用
z
z
z作为输出,神经元内部应用一个非线性函数
f
f
f到
z
z
z上:
y
=
a
=
f
(
z
)
y = a = f(z)
y=a=f(z)
这里的非线性函数称为激活函数,该函数的输出值称为激活值
a
a
a,我们已经见过的一种激活函数是Sigmoid函数:
y
=
σ
(
z
)
=
1
1
+
e
−
z
(3)
y = \sigma(z) = \frac{1}{1 + e^{-z}} \tag 3
y=σ(z)=1+e−z1(3)
这里神经元的输出
y
y
y和激活值
a
a
a相同,但在神经网络中,我们通常用
y
y
y表示整个网络最终的输出。把
(
2
)
(2)
(2)代入
(
3
)
(3)
(3),得到神经元的输出:
y
=
σ
(
w
⋅
x
+
b
)
=
1
1
+
exp
(
−
(
w
⋅
x
+
b
)
)
(4)
y = \sigma(w\cdot x + b) = \frac{1}{1 + \exp(-(w\cdot x + b))} \tag 4
y=σ(w⋅x+b)=1+exp(−(w⋅x+b))1(4)
除了Sigmoid之外,还有很多其他比较常见的激活函数。
常见激活函数
激活函数(activation function)通过计算加权和并加上偏置来确定神经元是否应该被激活,大多数激活函数都是非线性的。所有
ReLU
最常用的激活函数是修正线性单元(Rectified linear unit,ReLU),提供了一种非常简单的非线性变换。给定元素
x
x
x,ReLU函数被定义为该元素与
0
0
0的最大值:
ReLU
(
x
)
=
max
(
0
,
x
)
(5)
\text{ReLU}(x) = \max(0, x) \tag 5
ReLU(x)=max(0,x)(5)
ReLU函数通过将相应的激活值设为
0
0
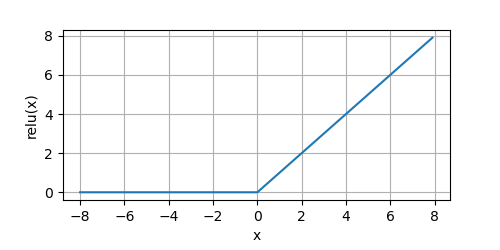
0,仅保留正元素并丢弃所有负元素。我们可以画出函数的图形感受一下:
from metagrad.functions import*from metagrad.utils import plot
if __name__ =='__main__':
x = Tensor.arange(-8.0,8.0,0.1, requires_grad=True)
y = relu(x)
plot(x.numpy(), y.numpy(),'x','relu(x)', random_fname=True, figsize=(5,2.5))
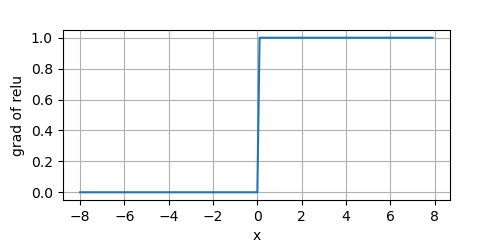
当输入为负时,ReLU函数的导数为
0
0
0,当输入为正时,ReLU函数的导数为
1
1
1。当输入为
0
0
0时,我们让其导数也为
0
0
0。
y.backward(Tensor.ones_like(x))
plot(x.numpy(), x.grad.numpy(),'x','grad of relu', figsize=(5,2.5))
由于ReLU的简单性,没有包含
e
x
e^x
ex,导致它的计算效率极高。同时它的梯度要么为
0
0
0,要么为
1
1
1,这使得优化变现得更好,减轻了困扰神经网络的梯度消息问题。
ReLU导数的函数图形如上图所示,我们可以看到,在
x
<
0
x < 0
x<0的一侧,梯度值永远是
0
0
0。因此,在反向传播的过程中,可能有些神经元的权重不会被更新(因为导数为
0
0
0)。这可能会导致永不激活的死节点(神经元)。这个问题可以被ReLU的变种:Leaky ReLU解决。
Leaky ReLU
Leaky ReLU是ReLU的改进版本,主要用于解决上面跳到的死节点问题,通过给所有负值赋予一个小的正斜率来解决
Leaky ReLu
(
x
)
=
m
a
x
(
a
x
,
x
)
(6)
\text{Leaky ReLu}(x) = max(ax, x) \tag 6
Leaky ReLu(x)=max(ax,x)(6)
通常这里的
a
=
0.01
a=0.01
a=0.01,为了看出效果。在画图时让
a
=
0.1
a=0.1
a=0.1,我们看一下它的图形:
y = leaky_relu(x)
plot(x.numpy(), y.numpy(),'x','leaky relu(x)', random_fname=True, figsize=(5,2.5))
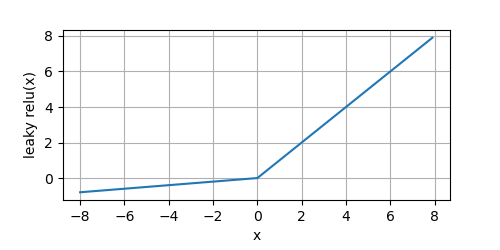
Leaky ReLU的优点与ReLU相同,同时对于负输入,其导数也变成了一个非零值(即
a
a
a)。
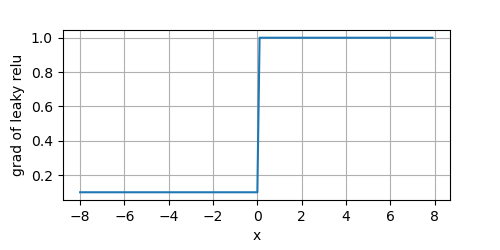
从上图可以看到,对于
x
<
0
x < 0
x<0的一侧,它们也有非零的导数。不至于出现死节点,但是由于
a
a
a通常很小,导致在在此侧的模型参数学习缓慢。
除了Leaky ReLU外,类似地还有两种变体,分别是Parametric ReLU和Randomized Leaky ReLU。
Parametric ReLU称为参数化的ReLU,即令Leaky ReLU中的
a
a
a变成了一个可学习的参数。
而Randomized Leaky ReLU让
a
a
a取自一个连续均匀概率分布。
Exponential Linear Unit
ELU(Exponential Linear Unit)也是ReLU的一种变体,类似Leaky ReLU修改在
x
<
0
x < 0
x<0侧的斜率,但在负区域不是一条直线,而是一条对数曲线。
ELU
(
x
)
=
max
(
0
,
x
)
+
min
(
0
,
α
∗
(
exp
(
x
)
−
1
)
)
(7)
\text{ELU}(x) = \max(0,x) + \min(0, \alpha *(\exp(x)-1)) \tag 7
ELU(x)=max(0,x)+min(0,α∗(exp(x)−1))(7)
通常
α
=
1
\alpha=1
α=1,我们画出ELU的图像:
y = elu(x)
plot(x.numpy(), y.numpy(),'x','elu(x)', random_fname=True, figsize=(5,2.5))
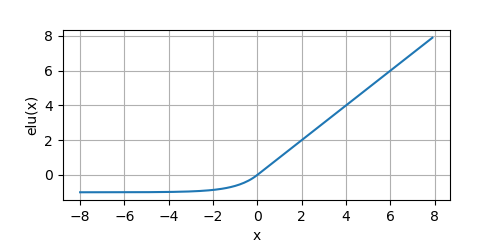
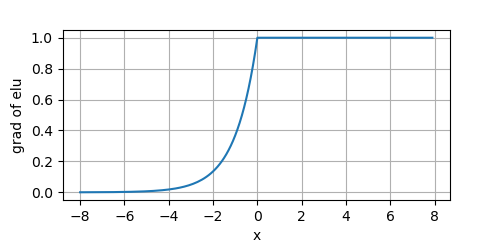
ELU在负值部分缓慢变得平滑,直到输出等于
−
α
-\alpha
−α,且
α
α
α是一个可调整的参数,它控制着ELU负值部分在何时饱和。但是引入了
e
x
e^x
ex。其导数的图像为:
SoftPlus
SoftPlus函数与ReLU函数接近,但比较平滑,也是单边抑制的。
SoftPlus
(
x
)
=
1
β
∗
log
(
1
+
exp
(
β
∗
x
)
)
(8)
\text{SoftPlus}(x) = \frac{1}{\beta} * \log(1 + \exp(\beta * x)) \tag 8
SoftPlus(x)=β1∗log(1+exp(β∗x))(8)
其中
β
\beta
β默认为
1
1
1,随着
β
β
β的增加,该函数越来越像ReLU。
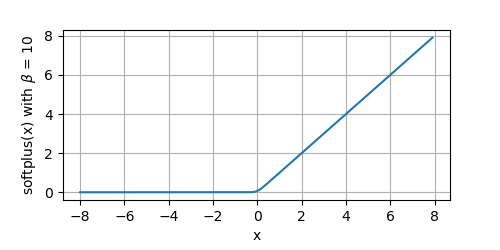
我们看一下默认情况下的函数图像:
y = softplus(x, beta=10)
plot(x.numpy(), y.numpy(),'x','softplus(x)', random_fname=True, figsize=(5,2.5))

当
β
=
10
\beta=10
β=10时,我们看一下函数图像:
y = softplus(x, beta=10)
plot(x.numpy(), y.numpy(),'x',r'softplus(x) with $\beta$ = 10', random_fname=True, figsize=(5,2.5))
其导数为:
d
d
x
Swish
(
x
)
=
d
d
x
(
1
β
log
(
1
+
exp
(
β
x
)
)
)
=
1
β
exp
(
β
x
)
β
1
+
exp
(
β
x
)
=
1
1
+
exp
(
−
β
x
)
=
σ
(
β
x
)
\begin{aligned} \frac{d}{dx}\text{Swish}(x) &= \frac{d}{dx} \left(\frac{1}{\beta} \log(1 + \exp(\beta x)) \right) \\ &= \frac{1}{\beta} \frac{\exp(\beta x) \beta}{1 + \exp(\beta x)}\\ &= \frac{1}{1 + \exp(-\beta x)} \\ &= \sigma(\beta x) \end{aligned}
dxdSwish(x)=dxd(β1log(1+exp(βx)))=β11+exp(βx)exp(βx)β=1+exp(−βx)1=σ(βx)
当
β
=
1
\beta=1
β=1,其导数就是
σ
(
x
)
\sigma(x)
σ(x)。我们来看下其导数图像:
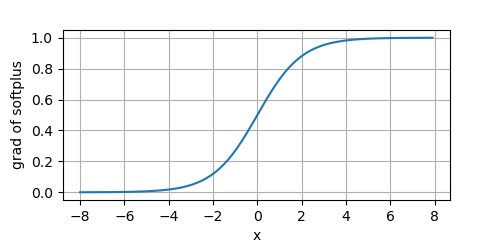
Swish
Swish在更深层次的模型上显示出比ReLU更好的性能。Swish的输入从负无穷到正无穷。函数定义为
Swish
=
x
∗
σ
(
x
)
=
x
1
+
exp
(
−
x
)
(9)
\text{Swish} = x * \sigma(x) = \frac{x}{1 + \exp(-x)} \tag 9
Swish=x∗σ(x)=1+exp(−x)x(9)
相当于是对输入
x
x
x进行了门控(通过
σ
\sigma
σ函数),我们看一下它的图像:
y = swish(x)
plot(x.numpy(), y.numpy(),'x','swish(x)', random_fname=True, figsize=(5,2.5))
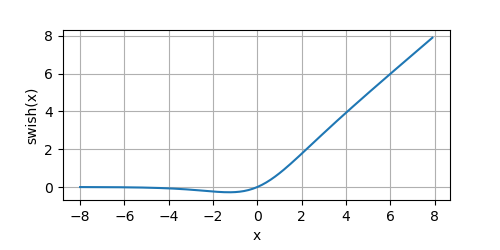
它的曲线都是光滑的,且处处可导。当
x
x
x增大时,函数值趋于无穷大;当
x
x
x减小时,函数值趋于常数。
Swish函数的导数为下面的公式:
d
d
x
Swish
(
x
)
=
d
d
x
x
σ
(
x
)
=
σ
(
x
)
+
σ
(
x
)
′
x
=
σ
(
x
)
+
σ
(
x
)
(
1
−
σ
(
x
)
)
x
\begin{aligned} \frac{d}{dx}\text{Swish}(x) &= \frac{d}{dx} x \sigma(x) \\ &= \sigma(x) + \sigma(x)^\prime x \\ &= \sigma(x) + \sigma(x)(1 - \sigma(x)) x \end{aligned}
dxdSwish(x)=dxdxσ(x)=σ(x)+σ(x)′x=σ(x)+σ(x)(1−σ(x))x
其导数的图像为:
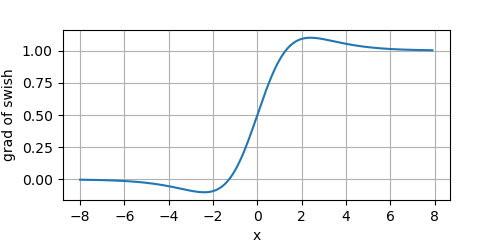
Swish的特性:
- 无上边界:不像sigmoid和tanh函数,Swish没有上边界的,因为它避免了在接近零的梯度中缓慢的训练时间——像sigmoid或tanh这样的函数是有界的,因此需要小心地初始化网络,以保持在这些函数的界限内。
- 曲线的平滑性:平滑性在泛化和优化中起着重要的作用。与ReLU不同,Swish是一个平滑的函数,这使得它对初始化权值和学习率不那么敏感。
- 有下边界:这有助于增强正则化效果( x x x左侧慢慢接近于 0 0 0,一定程度过滤掉一部分信息,起到正则化的效果)。
Sigmoid
Sigmoid函数将输入压缩为区间
(
0
,
1
)
(0,1)
(0,1)上的输出。因此,Sigmoid函数通常称为挤压函数(squashing function):
sigmoid
(
x
)
=
1
1
+
exp
(
−
x
)
(10)
\text{sigmoid}(x) = \frac{1}{1 + \exp(-x)} \tag {10}
sigmoid(x)=1+exp(−x)1(10)
当我们想要将输出看成二分类的概率时,sigmoid此时最常用。然而,sigmoid在隐藏层中较少使用,它通常被更简单、更容易训练的ReLU所取代。
下面我们画出sigmoid函数。
y = sigmoid(x)
plot(x.numpy(), y.numpy(),'x','sigmoid(x)', random_fname=True, figsize=(5,2.5))
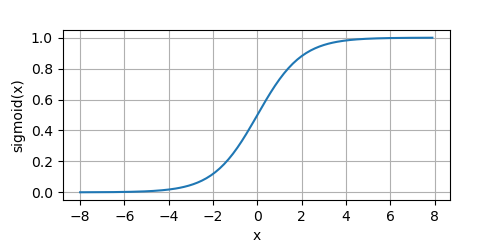
其导数计算如下:
d
d
x
sigmoid
(
x
)
=
d
d
x
1
1
+
e
−
x
=
0
×
(
1
+
e
−
x
)
−
1
×
(
1
+
e
−
x
)
′
(
1
+
e
−
x
)
2
=
−
(
−
e
−
x
)
(
1
+
e
−
x
)
2
=
1
+
e
−
x
−
1
(
1
+
e
−
x
)
2
=
1
1
+
e
−
x
−
1
(
1
+
e
−
x
)
2
=
1
1
+
e
−
x
(
1
−
1
1
+
e
−
x
)
=
σ
(
x
)
(
1
−
σ
(
x
)
)
\begin{aligned} \frac{d}{dx}\text{sigmoid}(x) &= \frac{d}{dx} \frac{1}{1 + e^{-x}} \\ &= \frac{0 \times (1+e^{-x}) - 1\times (1+e^{-x})^\prime}{(1 + e^{-x})^2} \\ &= \frac{- (-e^{-x})}{(1+e^{-x})^2} \\ &= \frac{1 + e^{-x} - 1}{(1+e^{-x})^2} \\ &= \frac{1}{1 + e^{-x}} - \frac{1}{(1 + e^{-x})^2} \\ &= \frac{1}{1 + e^{-x}} \left( 1 - \frac{1}{1 + e^{-x}} \right) \\ &= \sigma(x)(1 - \sigma(x)) \end{aligned}
dxdsigmoid(x)=dxd1+e−x1=(1+e−x)20×(1+e−x)−1×(1+e−x)′=(1+e−x)2−(−e−x)=(1+e−x)21+e−x−1=1+e−x1−(1+e−x)21=1+e−x1(1−1+e−x1)=σ(x)(1−σ(x))
其导数的图像为:
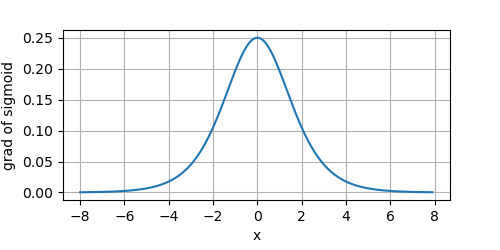
在深层网络中,Sigmoid存在三个问题:
- 饱和的神经元会让梯度消失,即在较大的正数或负数作为输入的时候,梯度就会变成零,使得神经元基本不能更新。
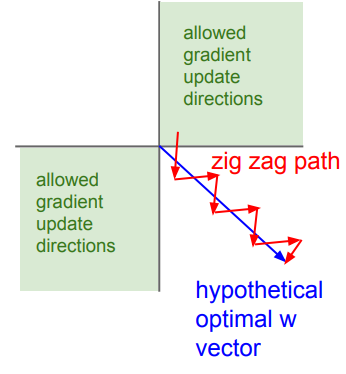
- 其输出不是以 0 0 0为中心的,而是 0.5 0.5 0.5。我们知道 d L d w = d L d z x \frac{dL}{dw} = \frac{dL}{dz}x dwdL=dzdLx,在深层网络中,由于上一层使用的是Sigmoid激活函数,导致该层的输入都是正数。即该层 w w w的梯度取决于 d L d z \frac{dL}{dz} dzdL,要么都是正的,要么都是负的,出现了zig zag问题。如下图所示,假设最佳更新路线是蓝线所示,由于zig zag问题,使其优化变成缓慢。
- 指数计算耗时
Tanh
tanh是sigmoid函数的变种,它的函数值变成范围从
−
1
-1
−1到
+
1
+1
+1,即变成了以
0
0
0为中心的。
tanh
(
x
)
=
e
x
−
e
−
x
e
x
+
e
−
x
(11)
\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} \tag{11}
tanh(x)=ex+e−xex−e−x(11)
我们来画出该函数的图像:
y = tanh(x)
plot(x.numpy(), y.numpy(),'x','tanh(x)', random_fname=True, figsize=(5,2.5))
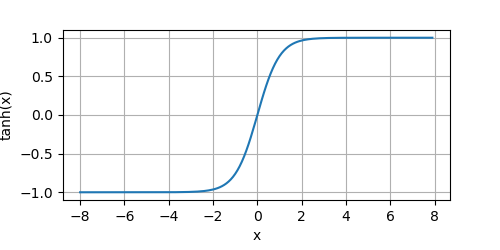
tanh函数具有平滑可微性,和将离群值映射到均值的良好性质。
为什么说tanh函数是sigmoid函数的变种呢?我们来推导一下:
tanh
(
x
)
=
e
x
−
e
−
x
e
x
+
e
−
x
=
e
x
+
e
−
x
−
e
−
x
−
e
−
x
e
x
+
e
−
x
=
1
+
−
2
e
−
x
e
x
+
e
−
x
=
1
−
2
e
2
x
+
1
=
1
−
2
σ
(
−
2
x
)
=
1
−
2
(
1
−
σ
(
2
x
)
)
=
1
−
2
+
2
σ
(
2
x
)
=
2
σ
(
2
x
)
−
1
\begin{aligned} \tanh(x) &= \frac{e^x - e^{-x}}{e^x + e^{-x}} \\ &= \frac{e^x + e^{-x} - e^{-x} - e^{-x} }{e^x + e^{-x}} \\ &= 1 + \frac{-2e^{-x}}{e^x + e^{-x}} \\ &= 1 - \frac{2}{e^{2x}+ 1}\\ &= 1 - 2\sigma(-2x) \\ &= 1 - 2(1 - \sigma(2x)) \\ &= 1 - 2 + 2\sigma(2x) \\ &= 2\sigma(2x) - 1 \end{aligned}
tanh(x)=ex+e−xex−e−x=ex+e−xex+e−x−e−x−e−x=1+ex+e−x−2e−x=1−e2x+12=1−2σ(−2x)=1−2(1−σ(2x))=1−2+2σ(2x)=2σ(2x)−1
因此,我们可以看到tanh只是sigmoid函数的缩放版本。
tanh函数的导数是:
d
d
x
tanh
(
x
)
=
d
d
x
e
x
−
e
−
x
e
x
+
e
−
x
=
(
e
x
−
e
−
x
)
′
(
e
x
+
e
−
x
)
−
(
e
x
−
e
−
x
)
(
e
x
+
e
−
x
)
′
(
e
x
+
e
−
x
)
2
=
(
e
x
+
e
−
x
)
2
−
(
e
x
−
e
−
x
)
2
(
e
x
+
e
−
x
)
2
=
1
−
(
e
x
−
e
−
x
e
x
+
e
−
x
)
2
=
1
−
tanh
2
(
x
)
\begin{aligned} \frac{d}{dx}\tanh(x) &= \frac{d}{dx} \frac{e^x - e^{-x}}{e^x + e^{-x}} \\ &= \frac{(e^x - e^{-x})^\prime(e^x + e^{-x}) -(e^x - e^{-x})(e^x + e^{-x})^\prime}{(e^x + e^{-x})^2} \\ &= \frac{(e^x + e^{-x})^2 - (e^x - e^{-x})^2}{(e^x + e^{-x})^2} \\ &= 1 - \left ( \frac{e^x - e^{-x}}{e^x + e^{-x}} \right)^2 \\ &= 1 - \tanh^2(x) \end{aligned}
dxdtanh(x)=dxdex+e−xex−e−x=(ex+e−x)2(ex−e−x)′(ex+e−x)−(ex−e−x)(ex+e−x)′=(ex+e−x)2(ex+e−x)2−(ex−e−x)2=1−(ex+e−xex−e−x)2=1−tanh2(x)
其中
d
d
x
e
x
=
e
x
\frac{d}{dx} e^x = e^x
dxdex=ex;
d
d
x
e
−
x
=
−
e
−
x
\frac{d}{dx}e^{-x} = - e^{-x}
dxde−x=−e−x
其导数图像如下所示:
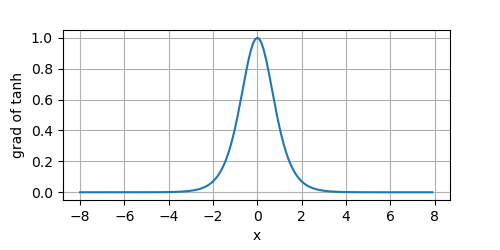
可以看到,当输入接近于
0
0
0时,tanh函数的导数接近于最大值
1
1
1。而输入在任一方向上越远离
0
0
0点,导数越接近
0
0
0。
Tanh的缺点类似Sigmoid,不过它是以
0
0
0为中心的,避免了zig zag问题。
如何选择激活函数
我们看了这么多激活函数,到底要如何选择呢?
在深层网络中,首先要尝试ReLU,它具有速度快的优点,如果效果欠佳;
那么尝试Leaky ReLU;
或者tanh这种以零为中心的;
另外,在RNN中常用sigmoid或tanh,作为门控或概率值。
完整代码
完整代码笔者上传到了程序员最大交友网站上去了,地址: 👉 https://github.com/nlp-greyfoss/metagrad
References
- DIVE INTO DEEP LEARNING
- Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification
版权归原作者 愤怒的可乐 所有, 如有侵权,请联系我们删除。