0
0

【搜索二叉树】迭代+递归实现&&K模型和KV模型

【二叉树初阶】二叉树的遍历+习题
接上一篇文章，适合刚学习二叉树的同学，里面也有习题讲解。
本篇文章将会介绍搜索二叉树的概念和模拟实现，以及它的应用Key模型和Key/value模型，简写为K模型和KV模型。

文章目录

🌌搜索二叉树的概念

搜索二叉树又称二叉树搜索树（Binary Search Tree），顾名思义是用来查找的，当树不为空时，有以下性质：

  1. 当左子树不为空时，左子树上的所以节点的值小于根节点
  2. 当右子树不为空时，右子树上的所有节点的值大于根节点
  3. 搜索二叉树每个节点的值key都不相同
  4. 搜索二叉树的左右子树都是搜索二叉树

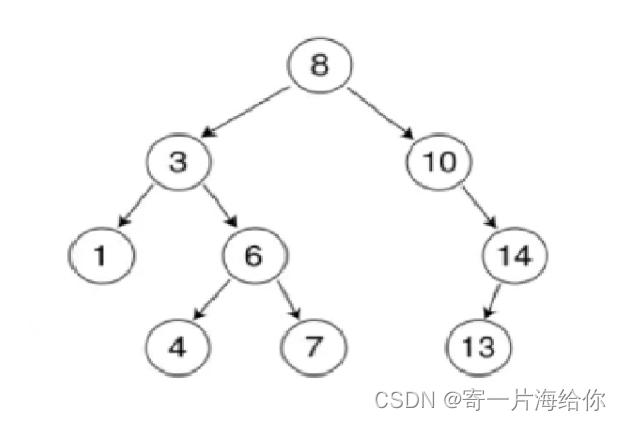
在这里插入图片描述

根据搜索二叉树的以上性质，可以排序+去重，中序遍历是可以排升序，每个节点的值不同可以去重,所以搜索二叉树也可称为排序二叉树

🌌BSTree的模拟实现

🌌迭代实现

大致框架：

#pragmaonce#include<iostream>usingnamespace std;namespace K
{template<classK>//节点structBSTreeNode{BSTreeNode(const K& key):left(nullptr),right(nullptr),_key(key){}structBSTreeNode<K>* left;structBSTreeNode<K>* right;
        K _key;};//树template<classK>classBSTree{typedef BSTreeNode<K> Node;public:BSTree():_root(nullptr){}//插入值为key的节点，插入失败返回falseboolInsert(const K& key);//查找值为key的节点，查找失败返回nullptr
        Node*Find(const K& key);//删除值为key的节点，删除失败返回falseboolErase(const K& key);//中序遍历(类外无法访问根，所以由子函数完成)voidInOrder();private://通过子函数完成中序遍历void_InOrder(Node* root);
        Node* _root;};}

🌌查找

先来实现BSTree的查找，比如要查找13，有如下过程，先从根开始比较，比根大就在右子树查找，比根小就在左子树查找，以此类推，如果走到nullptr还未找到，就说明树中没有该节点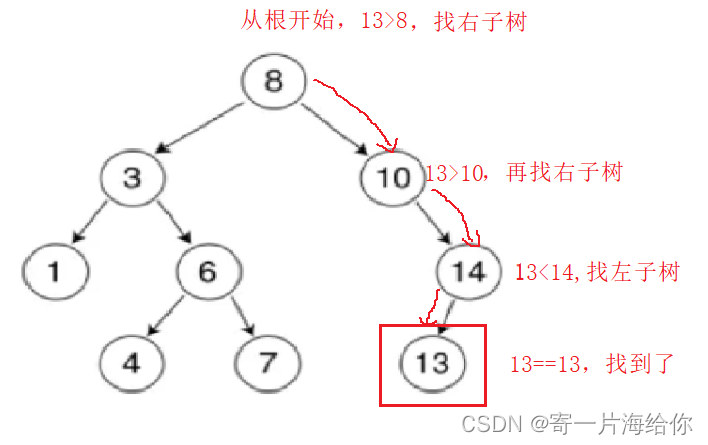
在这里插入图片描述所以BSTree最多查找高度次，如果以完全二叉树为例就是O(logN)，也就是说从10亿个数中找一个数最多只需要大约30次。当然如果BSTree退化为单支树，也就是查找的最坏情况O(N)，所以搜索二叉树是有缺陷的，后来引入了平衡搜索二叉树，两种实现AVL树和红黑树，之后的文章会讲解，这里就不在赘述了。

在这里插入图片描述

Node*Find(const K& key){//从根节点开始查找
    Node* cur = _root;while(cur){if(key > cur->_key)
            cur = cur->right;elseif(key < cur->_key)
            cur = cur->left;elsereturn cur;}//还未找到就返回nullptrreturnnullptr;}

🌌插入

假设要将9插入BSTree，定义一个cur从根开始比较，最后找到了要插入的位置，但是需要和10链接起来，所以还需要定义一个parent完成链接关系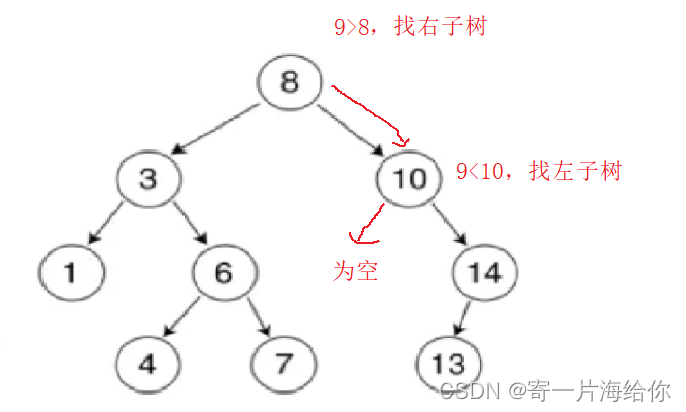
在这里插入图片描述

boolInsert(const K& key){if(_root ==nullptr){
        _root =newNode(key);returntrue;}
    Node* cur = _root;
    Node* parent =nullptr;while(cur){if(key > cur->_key){
            parent = cur;
            cur = cur->right;}elseif(key < cur->_key){
            parent = cur;
            cur = cur->left;}//插入的值和BSTree的值相等时，插入失败返回falseelsereturnfalse;}//cur找到插入的位置后，判断比parent大还是小，然后完成链接关系if(key > parent->_key)
        parent->right =newNode(key);else
        parent->left =newNode(key);returntrue;}

🌌删除

删除时BSTree的一个重难点，相比于上面的查找和插入要更复杂，考虑的情况也很多，我们先来一一分析
要删除的节点有以下三种情况，当然也可能树中没有这个节点：

  1. 只有一个孩子
  2. 没有孩子
  3. 有两个孩子

只有一个孩子和没有孩子可以统一处理，直接托孤，将要删除节点的孩子托给它的父亲，没有孩子就将nullptr托给它的父亲。
当节点的左为nullptr时，有以下三种情况（没有孩子的归类到左为nullptr的情况）

  1. 要删除的节点是父亲的右孩子
  2. 要删除的节点是父亲的左孩子
  3. 要删除的节点是根节点

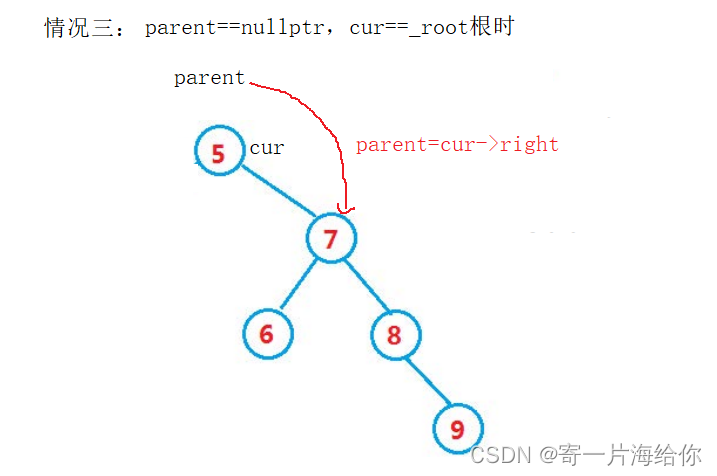
在这里插入图片描述在这里插入图片描述

同理当节点的右为nullptr时，也有以上三种情况。

再来讨论当要删除的节点有两个孩子时，这时候就不能用托孤了，需要采用替换法。
替换法：以要删除的节点为根，找到它左子树的最大值或右子树的最小值替换掉它的key，然后删除替换的节点

以找右子树最小值为例，右子树的最小值就是右子树最左边的节点，且它肯定没有左孩子

  1. 右子树最小值的节点是父亲的左孩子
  2. 右子树最小值的节点是父亲的右孩子

在这里插入图片描述

boolErase(const K& key){
    Node* parent =nullptr;
    Node* cur = _root;while(cur){if(key > cur->_key){
            parent = cur;
            cur = cur->right;}elseif(key < cur->_key){
            parent = cur;
            cur = cur->left;}//找到了else{//要删除的节点只有一个孩子(只有一个右孩子)或是没有孩子时if(cur->left ==nullptr){//要删除的节点是根节点时if(cur == _root)
                    _root = _root->right;else{if(parent->left == cur)
                        parent->left = cur->right;else
                        parent->right = cur->right;}delete cur;}//要删除的节点只有一个左孩子elseif(cur->right ==nullptr){if(cur == _root)
                    _root = _root->left;else{if(parent->left == cur)
                        parent->left = cur->left;else
                        parent->right = cur->left;}delete cur;}//要删除的节点有两个孩子else{
                Node* RightMin = cur->right;//寻找cur右子树的最小值，也就是右子树最左边节点
                Node* MinParent = cur;while(RightMin->left){
                    MinParent = RightMin;
                    RightMin = RightMin->left;}
                cur->_key = RightMin->_key;//如果右子树最小值在右边if(RightMin == MinParent->right)
                    MinParent->right = RightMin->right;else
                    MinParent->left = RightMin->right;delete RightMin;}returntrue;}}//未找到returnfalse;}

LeetCode上也有对应的题目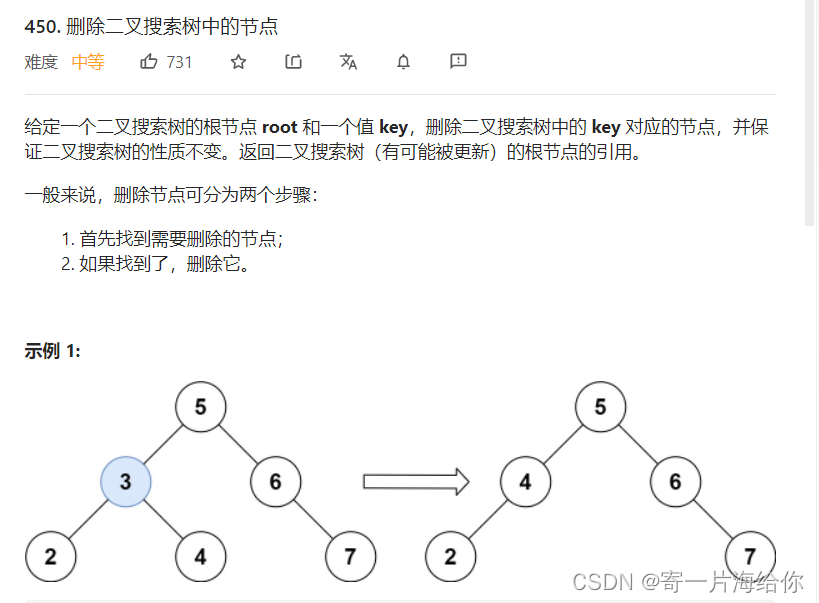
在这里插入图片描述

🌌递归实现

递归都需要通过子函数完成，因为类外无法访问根节点。

Node*_FindR(Node* root,const K& key){if(root ==nullptr)returnnullptr;if(key > root->_key)return_FindR(root->right, key);elseif(key < root->_key)return_FindR(root->left, key);elsereturn root;}boolFindR(const K& key){return_FindR(_root, key);}bool_InsertR(Node*& root,const K& key){if(root ==nullptr){
        root =newNode(key);returntrue;}if(key > root->_key)return_InsertR(root->right, key);elseif(key < root->_key)return_InsertR(root->left, key);elsereturnfalse;}boolInsertR(const K& key){return_InsertR(_root, key);}

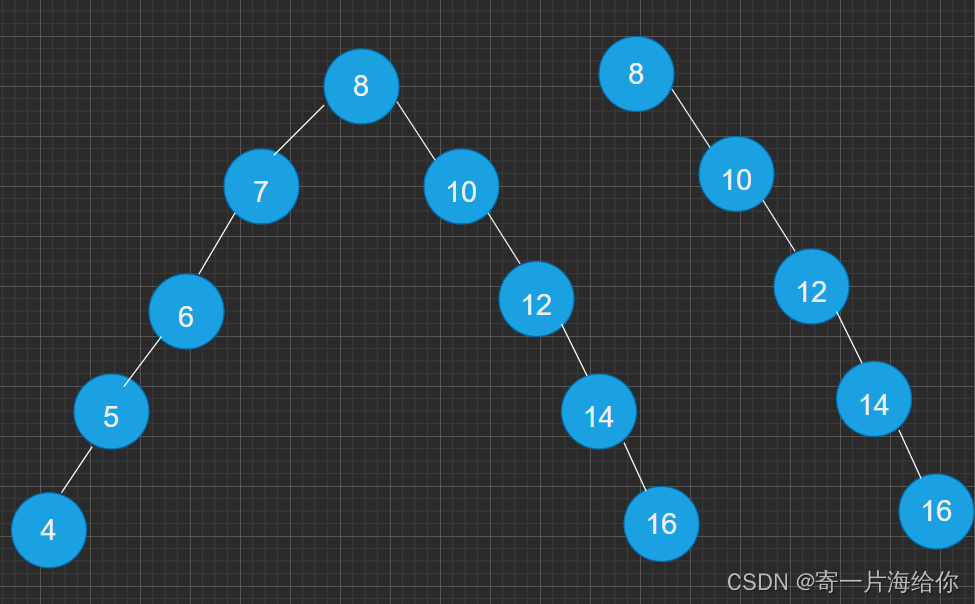
用递归实现插入，这里传的是引用，迭代法中的三种插入情况，都在root为nullptr这里处理，将root为根的情况也包含进来了，部分递归展开图：
在这里插入图片描述
删除也是传引用

bool_EraseR(Node*& root,const K& key){if(root ==nullptr)returnfalse;if(key > root->_key)return_EraseR(root->right, key);elseif(key < root->_key)return_EraseR(root->left, key);//找到了else{
        Node* del = root;//保存要删除的节点if(root->left ==nullptr)//这里的root是上一级root的左孩子或是右孩子，直接完成托孤，将这一级root的右孩子托给它的父亲
            root = root->right;elseif(root->right ==nullptr)
            root = root->left;else{
            Node* RightMin = root->right;while(RightMin->left){
                RightMin = RightMin->left;}//找到右子树最左边的值后，交换swap(RightMin->_key, root->_key);//递归到右子树删除//直接将要删除的节点有两个孩子，变成只有一个孩子或是没有孩子的情况_EraseR(root->right, RightMin->_key);}delete del;returntrue;}}boolEraseR(const K& key){return_EraseR(_root, key);}

🌌BSTree的应用

🌌K模型

K模型即只有key作为关键码，结构中只需要存储Key即可，关键码即为需要搜索到的值。上面模拟实现的就是K模型。K模型简单来说就是在不在。比如学校宿舍楼的门禁闸口，当我们刷卡过门禁时，机器根据卡上的信息查找当前楼栋是否有你的信息，如果没有就证明你不是这栋楼的。
ps：这只是一个例子，具体实现肯定不会用搜索二叉树实现
比如：给一个单词word，判断该单词是否拼写正确，具体方式如下：

  1. 以单词集合中的每个单词作为key，构建一棵二叉搜索树
  2. 在二叉搜索树中检索该单词是否存在，存在则拼写正确，不存在则拼写错误。

简答来说就是搜索单词是否在树里面，不在就拼写错误

🌌KV模型

KV模型就是通过一个值，查找相关联的另外一个值。每一个关键码key，都有与之对应的值Value，即<Key, Value>的键值对。比如中英文翻译<English,Chinese>，通过英文翻译出对应的中文，可以实现一个简单的英译汉词典。

  1. 以<英语单词，中文含义>键值对构建BSTree
  2. 通过英语单词key，找打对应的中文含义value

KV模型只需要在K模型的基础上稍作修改即可，加入一个模板参数V，具体实现在后面的源码给出

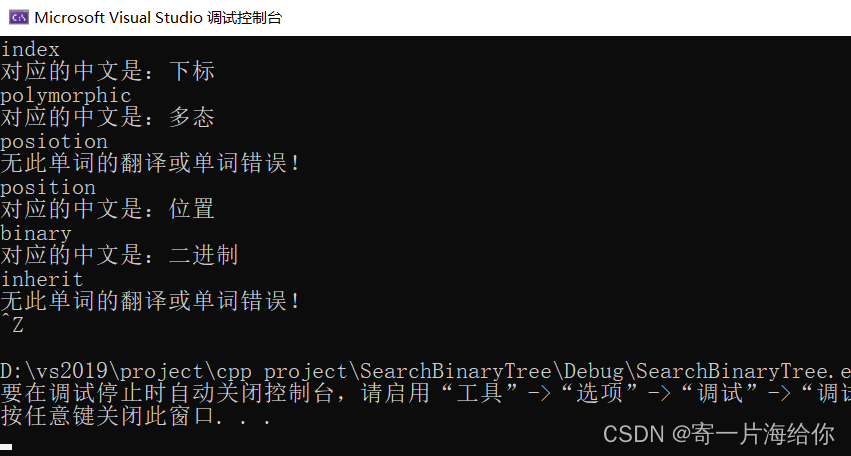
//根据输入的英文单词翻译出对应的中文voidTest1(){
    BSTree<string, string> dir;
    dir.Insert("index","下标");
    dir.Insert("binary","二进制");
    dir.Insert("position","位置");
    dir.Insert("inorder","中序");
    dir.Insert("polymorphic","多态");
    string s;while(cin >> s){
        BSTreeNode<string, string>* ret;
        ret = dir.Find(s);if(ret){
            cout <<"对应的中文是：";
            cout << ret->_value << endl;}else
            cout <<"无此单词的翻译或单词错误！"<< endl;}}

在这里插入图片描述同时KV模型还可以用来统计次数

//统计水果出现的次数voidTest2(){
    string arr[]={"香蕉","橙子","葡萄","橙子","香蕉","橙子","草莓","葡萄"};
    BSTree<string,int> count;for(auto& str : arr){
        BSTreeNode<string,int>* ret = count.Find(str);if(ret)
            ret->_value++;else
            count.Insert(str,1);}
    count.InOrder();}

在这里插入图片描述

🌌源码

#pragmaonce#include<iostream>usingnamespace std;namespace K
{template<classK>structBSTreeNode{BSTreeNode(const K& key):left(nullptr),right(nullptr),_key(key){}structBSTreeNode<K>* left;structBSTreeNode<K>* right;
        K _key;};template<classK>classBSTree{typedef BSTreeNode<K> Node;public:BSTree():_root(nullptr){}boolInsert(const K& key){if(_root ==nullptr){
                _root =newNode(key);returntrue;}
            Node* cur = _root;
            Node* parent =nullptr;while(cur){if(key > cur->_key){
                    parent = cur;
                    cur = cur->right;}elseif(key < cur->_key){
                    parent = cur;
                    cur = cur->left;}elsereturnfalse;}if(key > parent->_key)
                parent->right =newNode(key);else
                parent->left =newNode(key);returntrue;}
        Node*Find(const K& key){
            Node* cur = _root;while(cur){if(key > cur->_key)
                    cur = cur->right;elseif(key < cur->_key)
                    cur = cur->left;elsereturn cur;}returnnullptr;}boolErase(const K& key){
            Node* parent =nullptr;
            Node* cur = _root;while(cur){if(key > cur->_key){
                    parent = cur;
                    cur = cur->right;}elseif(key < cur->_key){
                    parent = cur;
                    cur = cur->left;}//找到了else{//要删除的节点只有一个孩子(只有一个右孩子)或是没有孩子时if(cur->left ==nullptr){//要删除的节点是根节点时if(cur == _root)
                            _root = _root->right;else{if(parent->left == cur)
                                parent->left = cur->right;else
                                parent->right = cur->right;}delete cur;}//要删除的节点只有一个左孩子elseif(cur->right ==nullptr){if(cur == _root)
                            _root = _root->left;else{if(parent->left == cur)
                                parent->left = cur->left;else
                                parent->right = cur->left;}delete cur;}//要删除的节点有两个孩子else{
                        Node* RightMin = cur->right;//寻找cur右子树的最小值，也就是右子树最左边节点
                        Node* MinParent = cur;while(RightMin->left){
                            MinParent = RightMin;
                            RightMin = RightMin->left;}
                        cur->_key = RightMin->_key;//如果右子树最小值在右边if(RightMin == MinParent->right)
                            MinParent->right = RightMin->right;else
                            MinParent->left = RightMin->right;delete RightMin;}returntrue;}}//未找到returnfalse;}boolFindR(const K& key){return_FindR(_root, key);}boolInsertR(const K& key){return_InsertR(_root, key);}boolEraseR(const K& key){return_EraseR(_root, key);}voidInOrder(){_InOrder(_root);
            cout << endl;}~BSTree(){Destroy(_root);}private://通过子函数完成中序遍历void_InOrder(Node* root){if(root ==nullptr)return;_InOrder(root->left);
            cout << root->_key <<" ";_InOrder(root->right);}
        Node*_FindR(Node* root,const K& key){if(root ==nullptr)returnnullptr;if(key > root->_key)return_FindR(root->right, key);elseif(key < root->_key)return_FindR(root->left, key);elsereturn root;}bool_InsertR(Node*& root,const K& key){if(root ==nullptr){
                root =newNode(key);returntrue;}if(key > root->_key)return_InsertR(root->right, key);elseif(key < root->_key)return_InsertR(root->left, key);elsereturnfalse;}bool_EraseR(Node*& root,const K& key){if(root ==nullptr)returnfalse;if(key > root->_key)return_EraseR(root->right, key);elseif(key < root->_key)return_EraseR(root->left, key);//找到了else{
                Node* del = root;//保存要删除的节点if(root->left ==nullptr)
                    root = root->right;elseif(root->right ==nullptr)
                    root = root->left;else{
                    Node* RightMin = root->right;while(RightMin->left){
                        RightMin = RightMin->left;}//找到右子树最左边的值后，交换swap(RightMin->_key, root->_key);//递归到右子树删除_EraseR(root->right, RightMin->_key);}delete del;returntrue;}}voidDestroy(Node* root){if(root ==nullptr)return;Destroy(root->left);Destroy(root->right);free(root);}private:
        Node* _root;};}namespace KV
{template<classK,classV>structBSTreeNode{BSTreeNode(const K& key,const V& value):left(nullptr),right(nullptr),_key(key),_value(value){}structBSTreeNode<K, V>* left;structBSTreeNode<K, V>* right;
        K _key;
        V _value;};template<classK,classV>classBSTree{typedef BSTreeNode<K, V> Node;public:BSTree():_root(nullptr){}boolInsert(const K& key,const V& value){if(_root ==nullptr){
                _root =newNode(key, value);returntrue;}
            Node* cur = _root;
            Node* parent =nullptr;while(cur){if(key > cur->_key){
                    parent = cur;
                    cur = cur->right;}elseif(key < cur->_key){
                    parent = cur;
                    cur = cur->left;}elsereturnfalse;}if(key > parent->_key)
                parent->right =newNode(key, value);else
                parent->left =newNode(key, value);returntrue;}
        Node*Find(const K& key){
            Node* cur = _root;while(cur){if(key > cur->_key)
                    cur = cur->right;elseif(key < cur->_key)
                    cur = cur->left;elsereturn cur;}returnnullptr;}boolErase(const K& key){
            Node* parent =nullptr;
            Node* cur = _root;while(cur){if(key > cur->_key){
                    parent = cur;
                    cur = cur->right;}elseif(key < cur->_key){
                    parent = cur;
                    cur = cur->left;}//找到了else{//要删除的节点只有一个孩子(只有一个右孩子)或是没有孩子时if(cur->left ==nullptr){//要删除的节点是根节点时if(cur == _root)
                            _root = _root->right;else{if(parent->left == cur)
                                parent->left = cur->right;else
                                parent->right = cur->right;}delete cur;}//要删除的节点只有一个左孩子elseif(cur->right ==nullptr){if(cur == _root)
                            _root = _root->left;else{if(parent->left == cur)
                                parent->left = cur->left;else
                                parent->right = cur->left;}delete cur;}//要删除的节点有两个孩子else{
                        Node* RightMin = cur->right;//寻找cur右子树的最小值，也就是右子树最左边节点
                        Node* MinParent = cur;while(RightMin->left){
                            MinParent = RightMin;
                            RightMin = RightMin->left;}
                        cur->_key = RightMin->_key;//如果右子树最小值在右边if(RightMin == MinParent->right)
                            MinParent->right = RightMin->right;else
                            MinParent->left = RightMin->right;delete RightMin;}returntrue;}}//未找到returnfalse;}~BSTree(){Destroy(_root);}voidInOrder(){_InOrder(_root);
            cout << endl;}private://通过子函数完成中序遍历void_InOrder(Node* root){if(root ==nullptr)return;_InOrder(root->left);
            cout << root->_key <<"："<< root->_value << endl;_InOrder(root->right);}voidDestroy(Node* root){if(root ==nullptr)return;Destroy(root->left);Destroy(root->right);free(root);}private:
        Node* _root;};//根据输入的英文单词翻译出对应的中文voidTest1(){
        BSTree<string, string> dir;
        dir.Insert("index","下标");
        dir.Insert("binary","二进制");
        dir.Insert("position","位置");
        dir.Insert("inorder","中序");
        dir.Insert("polymorphic","多态");
        string s;while(cin >> s){    
            BSTreeNode<string, string>* ret;
            ret = dir.Find(s);if(ret){
                cout <<"对应的中文是：";
                cout << ret->_value << endl;}else
                cout <<"无此单词的翻译或单词错误！"<< endl;}}//统计水果出现的次数voidTest2(){    
        string arr[]={"香蕉","橙子","葡萄","橙子","香蕉","橙子","草莓","葡萄"};
        BSTree<string,int> count;for(auto& str : arr){
            BSTreeNode<string,int>* ret = count.Find(str);if(ret)
                ret->_value++;else
                count.Insert(str,1);}
        count.InOrder();}}

以上就是搜索二叉树的实现和应用了。希望我的文章对你有所帮助，欢迎👍点赞 ，📝评论，🌟关注，⭐️收藏

在这里插入图片描述

标签： 算法 c++ 数据结构
本文转载自: https://blog.csdn.net/weixin_46016019/article/details/124536787
版权归原作者 寄一片海给你 所有， 如有侵权，请联系我们删除。
登录后发布评论

“【搜索二叉树】迭代+递归实现&amp;&amp;K模型和KV模型”的评论:

还没有评论
关于作者
...
overfit同步小助手
文章同步
相关阅读

机器人技术在安全领域的重要作用

安全学习记录——网络篇（一）

图腾柱PFC：HP1010为您的电动两轮车之旅提供绿色，高效，安全的动力

单元测试数据库回滚问题

这才是单元测试，之前我们都错了

【C语言基础】：字符函数和字符串函数

ChatGPT-Next-Web SSRF漏洞+XSS漏洞复现(CVE-2023-49785)

文章导航