架构成长之路 | 图解分布式共识算法Paxos教会协议

作者：码途 阿里全球技术服务团队

分布式共识算法是保证分布式一致性的基础，本文主要以简化类比的方式阐述了Paxos算法中的单法令教会会议（The Single-decree SYNOD）的算法。

一、分布式共识算法

分布式共识算法是保证分布式一致性的基础。我们在进行微服务开发的时候，都会尽量让自己的服务无状态（stateless），遇到部分需要存储的数据时，通常会将其往中间件转移 。比如持久化数据的存储往关系数据库转移，缓存的存取往Redis转移，文件的读写往OSS/HDFS转移，消息的收发往MQ转移。但是这些中间件又如何保证数据的一致性呢？如果用的是一个单机版中间件，则能够较容易地保证本地的一致性，但是这样会丧失可用性和扩展性。所以，很多中间件内部通常会使用分布式共识算法来保证分布式环境下的一致性，同时又能兼顾高可用和横向扩展。

分布式共识（consensus）和分布式一致性（consistency）它们的关系是怎样的呢？很多情况下我们会将两者混为一谈，但它们之间还是有细微的区别。一致性的解释有很多，这里选择用一种比较简单的解释：存储的数据之间不自相矛盾。一致性描述的是数据应该达到的结果，不自相矛盾包含了很多信息，数据能够持久化存储，副本之间的数据相同，满足业务上的各种规则等等；而共识则是一个过程，即大家关于某件事情（比如选举、分布式锁、全局ID、数据复制 等等）达成一致的过程。

常用的分布式共识算法有Paxos、Raft等等，还有一种更激进的说法："世界上只有一种分布式共识算法，那就是Paxos"。所以本专题以Paxos为引，逐步引出关于分布式共识、分布式一致性的更多内容。在进入Paxos讲解之前，首先需要了解一下关于分布式共识算法的两个基本特性：

• 安全性（safety）：所有的参与者对同一件事达成共识。例如对于选举，不会出现A、B认A为主，而C、D认D为主；
• 活性（liveness）：所有的参与者最终会对某一件事达成共识。也用选举来举例，不管谁当选，最终都会有人当选，而不是陷入死循环或死锁中

二、Paxos的历史

Paxos算法是Leslie Lamport于20世纪90年代在《The Part-Time Parliament》提出的，论文以一个虚构的Paxos小岛上选举的故事来描述整个算法，充满着各种隐喻，比较晦涩难懂。Lamport之后在2001年，通过在《Paxos Made Simple》中使用计算机领域的概念描述了一遍算法，但是依然很难理解。直到Google的Chubby横跨出世，作为它底层的分布式共识算法，Paxos也逐渐被大家熟知和认可。Lamport凭借他在分布式领域的贡献，最终于2013年获得图灵奖。

Paxos中包含两个协议，一个是单法令的教会协议（single-decree SYNOD），一个是多法令的议会协议（multi-decrees parliament），议会协议是教会协议的衍生版，本文主要讲解单法令议会协议。

三、背景设定

Long long ago，在遥远的爱琴海上，有一座与世隔绝的小岛，叫做Paxos……算了，还是用简单一点的例子吧。（以下故事，纯属虚构，如有雷同，就这么着）

我们团队一共有5个人，分别是我（小X）以及小A、小B、小C和小D。我们团队有个传统，就是每天中午之前，都会讨论一个困难的哲学问题——今天中午去哪儿吃？备选项也不多，去一食堂的餐馆吃拉面，或者说去二食堂的餐馆吃蛋炒饭。与其说吃什么，倒不如说我们就是想选个地方一起聊聊“八卦”，增进增进"感情"。

为此，每天中午吃饭之前，我们都会通过表决（ballot）的形式来进行投票（vote）。咱们的同学都比较忙，表决的时候有可能不在工位上，所以我们会锲而不舍的发起多轮表决，并且每轮表决只会简单的问在工位上的同学，吃面吗？或者是问吃米饭吗？其他人只需要回答**"我去"（投票），或者不回答（不投票）**。程序员都好懒哦，毕竟判断题比选择题简单，选择题比填空题简单，能回答一个字绝不再多说一个字。

四、要解决的问题

寻找出一种算法，在团队间关于"今天中午去哪儿吃？"（Decrees），达成友好的共识。

• 吃什么其实不那么重要，毕竟我们是要去增进"感情"的。所以一定要大家达成一致，不能两个人去吃面，三个人去吃米饭，这种"分裂"团队的事情，咱干不出来。
• 基于上面一点的目的，大家在表决的时候，也没有个人口味的倾向（能填饱肚子就行）。所以发起表决的人说吃啥，没有特殊情况，大家都会很捧场的说“我去”

五、怎么解决

Lamport从数学上证明了，如果用一种算法，它能满足了以下三点条件，就能很好地解决这个问题：

1. 每一轮表决都有一个唯一的编号，且表决之前能通过编号进行大小比较。不要求表决是严格按照编号的顺序发起的；

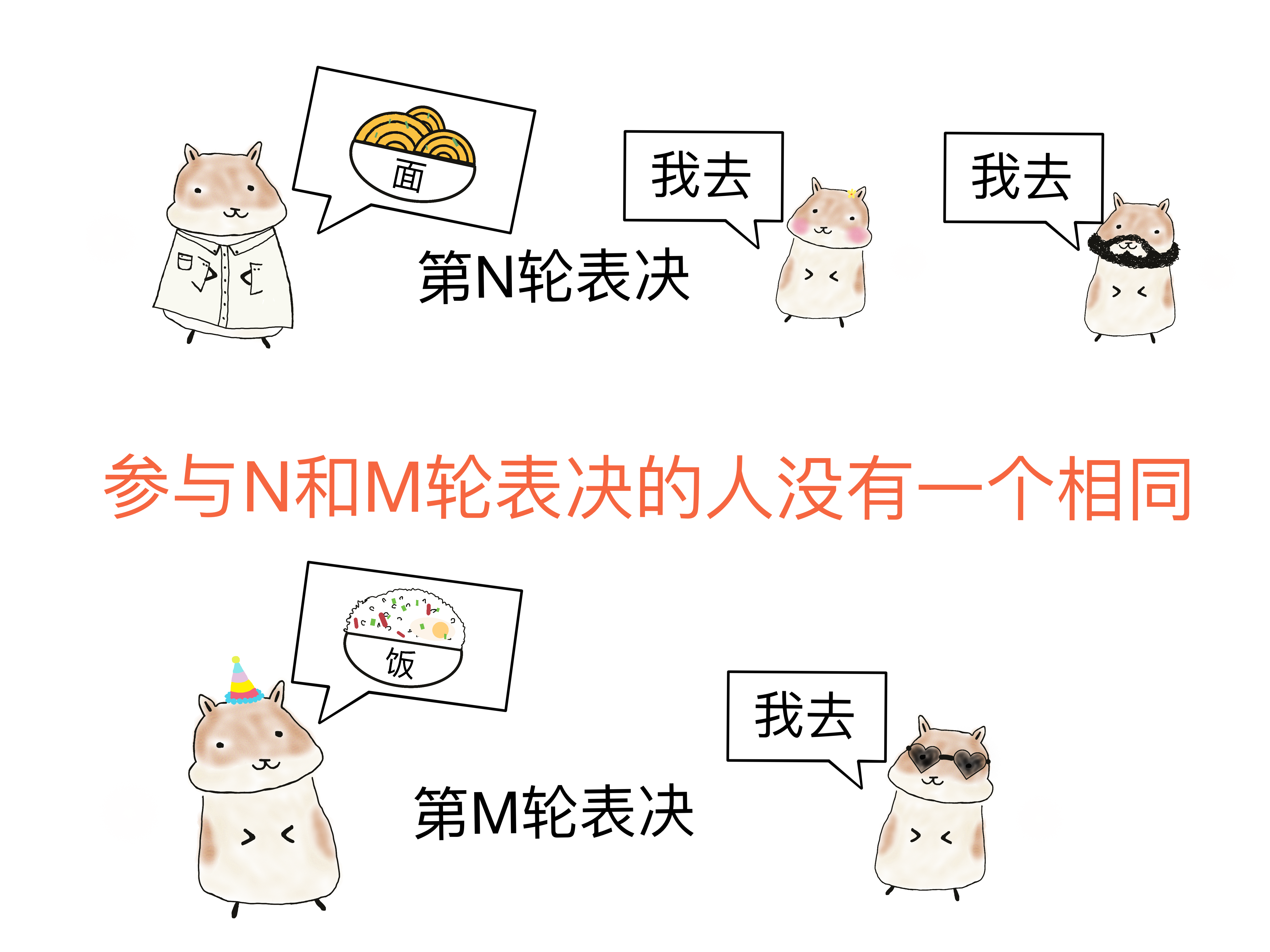
1. 任何两轮表决的参与人（在工位上的人）之间，至少有一个人是同一个人。

例如第N轮表决有小A和小D参加，参与第M轮表决变成了我和小B、小C参加。这两轮表决找不出一个共同的人，这就违背了第2点条件；

1. 对于任何一轮表决，如果参与表决的人在之前投过票。那么这一轮表决询问的餐馆，就必须是之前投过票的人里，最大的那轮表决询问的餐馆。

有点拗口，举个栗子。小B准备发起第三轮表决，参与表决的人有小A和小D。小A在第一轮发起过表决，问大家要不要吃面；小D在第二轮投过票，那一轮问的是要不要吃米饭。那么，按照第3点条件，小B发起的第三轮投票，只能问大家要不要吃米饭。（小A给第一轮的面投票了，发起的表决默认给自己投票了； 小B和小D给第二轮的米饭投票了，所以参与第三轮表决的人，投过的票里最大那一轮是就是第二轮的米饭）。

这里又引出另外一个问题，如果参与这轮表决的人都没投过票（比如第一轮），那么随便问一家就好了。

只要我们不断地发起表决，每一轮表决都满足以上三点条件。那么直到某一轮表决，所有参与人都说了“我去”（不一定所有人都参与了这一轮表决，可能有的人不在工位上；参与的人也不一定都会说“我去”，可能有的人正在开会），我们能就今天中午去哪儿吃达成共识（具体的证明步骤放到最后）。

满足这三点条件的算法，只保证了安全性，但并不一定保证活性。所以有可能我们今天中午啥都吃不了。（*Lamport提出了一种既满足安全性，又基本满足活性的实现方式，详情可参见附录中的"完整教会协议"*）

六、初步协议（The Preliminary Protocol）

算法的三点条件只是“指导原则”，要细化到可落地、可执行的方式，还有很长一段路要走。不要慌，我们一点一点地“打穿”它。

为了满足算法的第一点条件，即“每一轮表决，都有一个唯一的编号。且表决之前能通过编号进行大小比较”。每个人记录都需要记下自己发起过的表决编号，这样在下次发起表决的时候，能保证编号在本人的范围内是唯一的（且可比较）；那么如何保证这个编号在所有人范围内都是唯一且可比较的呢？在表决的编号中加入每个人的唯一标识（名字、工号、身份证号等等），这个标识也是可以进行排序的，这样每个人都得到一个独立的表决号空间。举个栗子：(13，小A) < (13, 小X) < (15，小A)。

为了满足算法的第二点条件，即"任何两轮表决的参与人（在工位上的人）之间，至少有一个人是同一个人"。只需要参与每一轮表决的人数，大于总人数的一半即可；如果参与人数小于等于总人数的一半，那就不能发起这轮表决，或者说这轮表决无效。这个可以通过一个简单的反证证明，假设有两轮投票B和C，包含的人数都大于总人数 P 的一半，但是它们的参与者里面没有相同的一个人（即交集为空）。那么B的参与者的人数范围Pb > P/2，C的参与者的人数范围Pc > P/2，所以 Pb + Pc > P；又因为假设中的B和C的参与者没有交集，所以P - Pc >= Pb，即 Pb + Pc <= P，这和前面的推导出的结论矛盾了，所以假设不成立。

为了满足算法的第3点条件，即"对于任何一轮表决，如果参与表决的人在之前投过票，那么这一轮表决决定的餐馆，就必须是之前投过票的人里，最大的那轮表决询问的餐馆"。就这一点，我们需要精心的设计整个表决的过程，以满足条件。

完整步骤

1. 小A先生成一个唯一的表决编号，假设是十。然后给每个在工位上的人说: "我准备开始第十轮表决了"（NextBallot）。（在这里用小A只是一个例子，任何人在任何时候都可以发起表决，甚至是并发地发起表决）；​

1. 小B听到之后，可以回答小A: "我参与第十轮表决，并且我在之前的第八轮表决中投了吃面"（LastVote）。其他人亦是如此回答。在这里有一点很重要，就是回答了小A的人，都需要做出一个承诺（promise）：我不再回答上次投票的表决和这轮表决之前的其它询问。对于小B来说，就是当有人说"我准备开始第九轮表决了"的时候（不要觉得奇怪，算法只要求表决编号唯一且可比较，并没有要求是有序的），他不做任何回应，这样才能保证对A做出的回答是有效的。不然小B刚给小A说在第八轮投了吃面，转头就给第九轮投了米饭；​

1. 当小A从大多数人那里得到回答之后，他就可以将这些人圈定为参与本轮表决的人。并且从这些人的回答中，得到本次表决需要询问的餐馆，这样就能满足算法的第3点条件。在这里假设得到要问的是吃面。然后小A就可以正式开始表决了，他依次去问这些人："要不要去吃面"（BeginBallot）；

1. 参与这轮表决的人，在听到小A问要不要去吃面后，根据自身情况决定要不要回答"我去"（Voted）。因为从第2步到现在，可能有其他人发起了第十一轮表决。大家的承诺可不保证不去回应更大轮次的表决，如果有人回应了更大的轮次并做出承诺，那么他在这里就不能说"我去"了；

1. 如果参与第十轮的所有人，都对小 A 说了"我去"，那么他就可以得出结论——今天中午去吃面。并且将这个消息（Success）奔走相告给团队里的每个人（不只是参与这轮投票的人）；

整个步骤有点像一个"三阶段提交"的过程，并且满足了算法的3点条件。再辅以数学上的证明，从而保证了算法的安全性。

可能出现的异常情况

上一节完整的叙述了初步协议的正常步骤，那么这些步骤如果出现了异常，会对算法产生什么样的影响呢？

1. 第1步中可能出现的异常情况：1. ​在生成表决号时如果出现了问题，这轮表决就无法发起；2. 如果在给其他人说"准备开始表决"的时候，只有小部分人在工位，或者大部分人都没听到。那么第3步的条件就无法达成，也不会有正事的表决。而听到且回应了的一小部分人，他们只是做出不投某些票承诺，并没有给这轮表决投票；
2. 第2步中可能出现的异常情况：1. 接受人已经对别的表决做出承诺了（严格来说这不算异常情况）。这个就不予以回应，也不做出新承诺。当多个人并发尝试发起表决时，可能遇到这个情况。这个时候谁都没有法开展表决，就看谁能通过新的更大的表决号，先争取到大多数人的参与；2. 接受人做出了承诺，但是他的回应没被发起人听到。如果只是小部分人，不影响第3步表决的正式开始；如果是大部分人，则打断第3步执行，不会正式开始表决；
3. 第3步中可能出现的异常情况：1. 一直收不到大多数人的"我参加……"，那就一直不开始正式表决；2. 提出的"去不去xxx吃饭问题"，没有被参与人听到。只要有一个参与人未听到这个问题，或为对这个问题做出回应，那么表决就没有结束。没有结束的表决，不会影响算法的安全性。
4. 第4步中可能出现的异常情况：1. "我去！"没被发起人听到。同3.b 。
5. 第5步中可以出现的异常情况：1. 最后的结论，没有传达到所有人。那这些人会认为还没有达成共识，而继续发起表决。通过附录"数学证明"中的引理，可以保证后续的表决，会得到相同的结论。

异常宕机

如果某些人暂时离开，之后又回工位了，这对算法的安全性不造成影响（可恢复性宕机）。但是如果有人离开又回来之后，发现忘记了之前记录的承诺和投票，记录的小本本也不见了（不可恢复性宕机），这种情况下，这个算法就无法满足安全性。设想以下场景：

小A发起了第一表决，问大家要不要去吃面。小B和小C积极响应并且投了票。然后小B去阳台找小D和小X，回来之后小B把第一轮的事情给忘了。这个时候，小D想起还不知道中午吃啥，于是发起了第二轮表决，给小B和小X说他准备开始第二轮表决了，小B和小X回应小D说他们都没投过票，于是小D随机选了米饭正式表决。小B和小X也都说了“我去”。这个时候算法的安全性就被破坏了，小A和小C得到结论是去吃面，小B、小D和小X得到的结论是去吃米饭。

网络分区

如果出现了网络分区的情况（这是不可避免的），对应到例子里就是团队的5个人被临时分散到不同地方去开会了。这时会有两种情况：

1）每个分区都只包含少数人（不超过2人），那么算法的第2步和第4步都会卡住，从而影响算法的活性，但并不影响安全性；

2）（最多）有一个分区包含了大多数人（不少于3人），这个分区中的人能继续通过算法得出结论，而其他分区的人，只能等到网络恢复之后，通过新的表决来同步这个结论。

七、写在最后

Paxos算法的教会协议是一个单法令的协议，也就是说它只能就一件事情达成一致的决定。那么它有什么样的用途呢？如果将这个事情换成一个具体命令，就能联想到它的各种用法。比如将法令换成“谁来做Leader？”就可以用于选举；将法令换成“谁能持有这个资源的锁？”，就能用于分布式加锁。但是受限于“单法令”，有很多用法都只能完成一部分，而更为实用的多法令议会协议，是从教会协议衍生出来的，并且高度依赖教会协议中的算法。

八、附录

基础协议（The Basic Protocol）

在初步协议中，每一个人都需要在小本本里，记下三个东西：

• 自己发起的所有表决的编号，以便再发起表决时，能生成一个新的唯一编号；
• 自己的每一次投票，即在哪些轮的表决说了"我去"，还要记下这些表决问的是哪个餐馆；
• 自己在初始协议的第2步回应之后，做出的承诺，白纸黑字记下来比较可靠。

需要记的东西着实有点多，多来几轮表决，多来几天，大本本都搞不定。所以机智的我（记住，这是一个虚构的故事）又登场了，我简化了初始协议，这样每个人只需要记录以下三个东西：

• 只用记下上一次发起的表决的编号；
• 投过的票里，只用记下最大编号的那一轮表决的编号，和它问的餐馆；
• 类似初始协议第2步的承诺，只用记下表决编号最大的承诺。比如我先回应了第十轮表决，做出来承诺；然后又回应了第十一轮表决，也做出了承诺。这个时候我可以把第十轮的承诺擦掉，记下第十一轮的承诺就行；​

注意这里的区别：初始协议是需要几下每一个编号、每一次投票、每一个承诺，因为初始协议是运行并发地发起表决的；但是基础协议只需要记住一个编号、一次投票和一个承诺。所以……基础协议不允许并发地表决，一旦发现了过时的表决或者响应，都不予理睬；一旦发现了更新的表决或者响应，抛弃掉老表决的记录，转而响应更新的表决。简化后的基础协议具体步骤如下：

1. 小A根据他记录的上一次发起的表决编号（记录的第一项内容），计算出一个新的表决编号b ，然后给每个在工位上的人说："我准备开始第b轮表决了"。
2. 小B听到了小A的问题之后，发现这轮表决编号比他做过的承诺的表决编号（记录的第三项内容，比如说是九）还大，那么就回应小A说"我参与第十轮表决，并且我在之前的第八轮（记录的第二项内容）表决中投了吃面"，然后小B将记录的第三项从"我给第九轮表决做出了承诺"改成"我给第十轮表决做出了承诺"；反之如果小B记的承诺编号比十大，那就不回应小A。
3. 小A收到了大多数人的针对第十轮表决的回应之后，就可以正式开始表决，圈定参与人和选择询问的餐馆同初始协议的第三步一致。小A依次去问这些人，要不要去吃面。
4. 小A问到小B时，小B检查自己的小本本，如果发现第二项记录的承诺还是十，那就给小A说"我去"；否则就不回答小A。
5. 当参与表决的每一个人，针对第十轮的表决都说了"我去"，那么他就可以得出结论——今天中午去吃面，并且将这个结论奔走相告给团队里的每个人（不只是参与这轮投票的人）。
6. 团队里的每个人，一旦听到了小A宣布的结论，也都知道了今天中午去吃面。​

完整教会协议（The Complete Synod Protocol）

基础协议同初步协议一样，保证了一致性，但是并不保证一定能达成决定。所以为了能尽早达成一致的决定（看来大家还是不喜欢挨饿的），完整协议在保持基础协议6个步骤的同时，除了要求每个人都能积极执行或响应第2~6步，更重要的是完整协议规定了大家在什么时候发起表决（第一步）。

为什么何时发起表决很重要？因为存在以下情况，会导致大家一直都没法达成决定：

• 一直没有人来发起表决，当然也没法达成决定。
• 太多人持续发起新表决，也可能没法达成决定。基础协议只能串行处理表决，每次发起了更新的表决，都会将可能正在进行中的表决中断。

​

这就要求我们必须要发起新的表决，但是又不能太频繁的发起新的表决（就是这么矛盾）。为了解决这个问题，完整协议增加了一个选生活委员的前置步骤。

如何选出这个生活委员呢？最简单的一个办法就是选还在工位上的工号最小的那个，可行的步骤如下：

1. 每个还在工位的人，每隔5分钟就告诉其他人自己的工号是多少。小A跟小B、小C说自己的工号是123456，小B跟小A、小C说自己的工号是654321，小C跟小A、小B说自己的工号是 55555；
2. 然后每个人每过10分钟就检查一下，看下之前10分钟有没有听到别人的工号比自己小的。如果有，那就证明自己当选生活委员无望；如果没有人工号比自己的小，那就恭喜自己当选了，可以发起新一轮的表决了；
3. 在这个10分钟的检查期内：如果小X又回到工位，然后跟小A、小B、小C说自己的工号是11111，那么小A就知道自己无望当选了；但是如果这时小A离开了工位，那么小B和小C什么也不会做，等到下一个10分钟再看；​

小A当选了生活委员之后，需要做些什么呢？

• 首先是先发起新一轮的表决；
• 其次，如果在执行第三步或第五步的时候，过了很久（可能是有人离开工位了；也有可能是一个工号更小的人回了工位，认为自己当选了生活委员，发起了更新的表决）都没有收到大家的响应，那么就需要重新发起新的一轮表决（前提是他还当选着）；
• 此外，为了避免新发起的表决，一开始过时了（小A发起了第十轮表决，但在此之前，小B已经给第十一轮表决承诺了），所以小A需要从其他人那儿了解到他们做出的承诺，并以此来调整自己之后发起表决的编号。有两种方式：- ​在初步和基础协议的第二和第四步中，遇到这种情况，小B不会给小A任何回应。但是到了完整版协议中，小B会告诉小A："我不参加第十轮投票了，因为我已经给了第十一轮承诺"，或者是："我不能确定要不要去吃面，因为我已经给了第十一轮承诺"。这样小A就知道自己的第十轮表决时过时的，转而去发起第十二轮表决。- 每个人隔段时间都告诉其他人，自己发起过的最大一轮表决编号是多少。比如小C每过5分钟就告诉小A和小B，自己之前发起过第十一轮表决。等到小A当选生活委员的时候，就会跳过第十轮表决，发起第十二轮表决。

完整协议的很多步骤，都强依赖时间（即每个一段时间做XX事情），但它并不要求这个时间完全精确，只要在可接受的范围内即可。

证明过程

(这一部分有点烧脑，对证明过程不感兴趣的话可以略过)

前面提到了，我们只要满足算法的三点条件，就能达成一致的决定。这并不是随便说说的，下面给出了完整的数学证明：

如果我们的所有表决，都满足算法的三点条件的情前提下。假设参与的小A、小B和小C都在第十轮表决，问大家去不去吃米饭，说了"我去"（按照算法，此时已达成了去吃米饭的一致决定）。

这里的证明用下反证法：假设第十轮之后的表决中（也满足算法的三点条件），还有表决在问大家要不要去吃面。基于这个假设成立的结论，我们一步一步地推导下去：

1. 首先从第十轮之后，问去不去吃面的表决中，取最早的一轮表决C。因为我们的假设，所以 C一定存在；
2. C的轮次肯定大于第10轮。很显然成立，因为我们就是这么假设的；
3. 第十轮里投票的人，和C轮里参与的人，至少有一个相同的人。这也很显然也成立，因为所有的表决，都必须满足算法的第2点条件；
4. 参与C轮表决的人中，之前投过票的最大表决M，那么M的轮次 >= 十。参与C轮表决的人可以分为两组：第一组是参与过第十轮投票的人，因为算法的第2点条件，这组里面一定有人，所以这一组的M1 >= 十（如果他们后面又投票，M1就大于十）；第二组是没参加过第十轮投票的人，这一组可能没人，有可能只在第十轮前投过票，也有可能只在第十轮之后投过票，更有可能部分人第十轮前投票，部分人第十轮之后投票，所以这一组的M2可以是小于C轮次的任意值。然后两组再取其大，M = Max(M1, M2) >= 十；
5. M也是算法的3点条件的，这是我们的前提；
6. 所以，M问的餐馆和C问的餐馆是一样的，也就是去吃面。因为M和C轮表决都满足算法的第3点条件；
7. M问的餐馆和第十轮问的餐馆不一样。根据上面一步推导，M轮问的是吃面，第十轮问的是米饭；
8. M的轮次必定大于十。这个比第4步推导更进了一步，消除了等于这种情况。因为第7步，我们得出M和第十轮问的餐馆不一样，又因为算法的第一点条件（每轮投票都有唯一的编号），可以推导M的轮次不等于十；
9. 因为第7、8步的推导，和初始假设成立的结论，得出M是一个在第十轮之后，问大家要不要去吃面的表决；
10. M的轮次一定是小于C的轮次的，因为根据第4步，M的定义就是"参与C轮表决的人中，之前投过票的最大表决"；
11. 矛盾出现了。C的定义在第1步中的定义是"第十轮之后，问去不去吃面的表决中，最早的一轮表决"，而M根据第9步的推导，它是"第十轮之后，问大家要不要去吃面的表决"，又因为第10步我们得出"M的轮次一定是小于C的轮次的"，这三点是冲突的。

所以通过反证法和这11步推导得出的矛盾，我们的初始假设不成立。"假设第十轮之后的表决中（也满足上面的三点条件），还有表决在问大家要不要去吃面" 这个假设不成立。换句话说，通过我们的证明，得出了一个引理（Lemma）：

所有表决都满足算法的3点条件的情况下，在表决投票得出一致的餐馆后，后续的表决中不会再问出要不要去其它餐馆的问题了。

通过这个引理，我们还能够得出其他两个定理（Theorem）：

定理一：所有表决都满足算法的三点条件的情况下，任何两轮成功的表决（所有参与表决的人都投了票），它们问的餐馆是一样的；

定理二：在已有表决都满足算法的三点条件的情况下，在后续新开展的表决中，一定存在满足算法的3点条件且成功的表决。算法虽然不保证一定能达成决定，但通过这点至少能证明满足三点条件之后，不会死锁。

定理二的证明过程如下，假设满足定理的表决为B，那么：

1. 可以通过很多已有算法（雪花算法）来选择一个比已有轮次都更大，且唯一的B的轮次。这样B就满足了算法的第1点条件；
2. 只要每一轮表决（已有的和B），都选择所有人中的大多数（参与人数大于总人数的一半，例子中即3人），那么B的参与者也能够满足算法的第二点条件；
3. 如果参与B的人之前都没投过票，那么B可以随便决定那个餐馆；如果参与B的人之前投过票，那么B问的餐馆就是这些人之前投票的最大一轮表决问的餐馆。这样B就满足了算法的第三点；
4. 又因为背景中的设定，每个人没有口味偏好，一般情况下参与了表决，就会投票。所以经历足够多轮的表决之后（每一轮都按照以上三点，定出一个满足算法的B），总能有一轮表决参与的人都投了票，从而让这轮是一轮成功的表决。