【经典算法2——直接插入排序】

活动地址：CSDN21天学习挑战赛

经典算法2——直接插入排序

• • 一、什么是排序？- 二、内部排序和外部排序- 三、内部排序的方法- 四、插入类——直接插入排序- - 1.基本思想- 2.实例分析- 3.代码实现- 4.运行结果展示- 5.视频讲解- 五、时间复杂度与空间复杂度分析- - 1.时间复杂度- 2.空间复杂度- 六、说明

一、什么是排序？

排序是计算机内经常进行的一种操作，其目的是将一组“无序”的记录序列调整为“有序”的记录序列。
例如：将下列关键字序列
14，15，92，65，35，89，79，32
调整为
14，15，32，35，65，79，89，92

二、内部排序和外部排序

若整个排序过程中不需要访问外存便能完成，则称此类排序问题为内部排序；反之，若参加排序的记录数量很大，整个序列的排序过程不可能在内存中完成，则称此类排序问题为外部排序。

三、内部排序的方法

内部排序的过程是一个逐步扩大记录的有序序列长度的过程。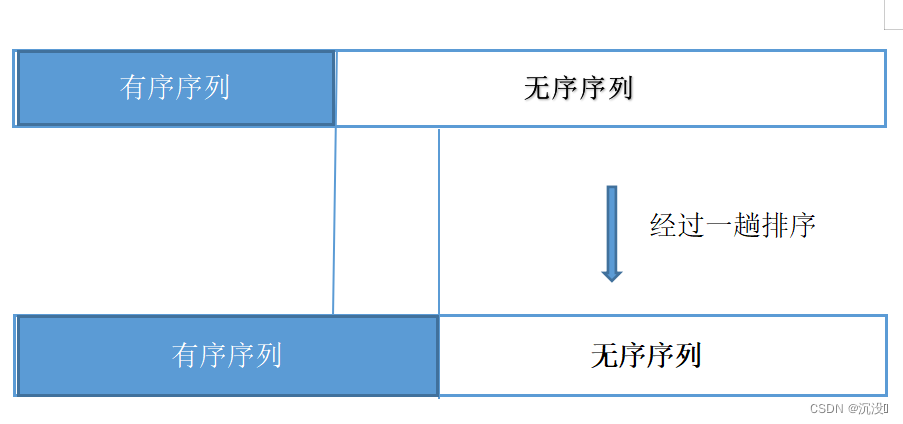

基于不同的“扩大”有序序列长度的方法，内部排序方法大致可分为：插入类、交换类、选择类、归并类、其它方法。

四、插入类——直接插入排序

1.基本思想

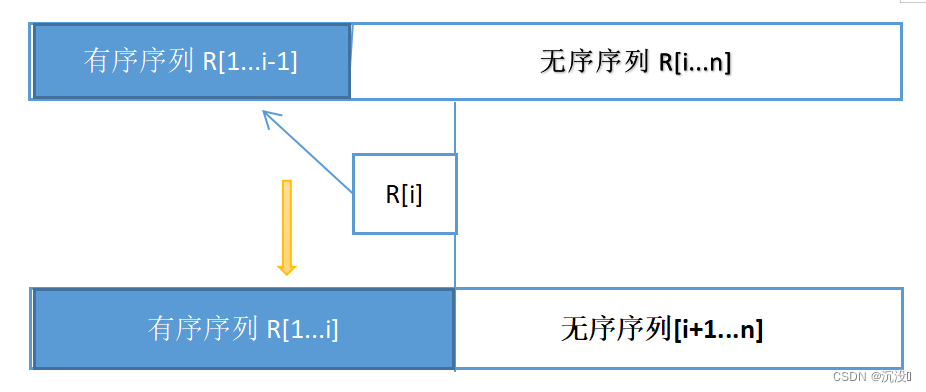
2.实例分析

1）例如：将下列关键字序列
14，15，92，65，35，89，79，32
调整为
14，15，32，35，65，79，89，92
2）第一趟排序第一个数14不动，将15拿出来与14比较，比14小，所以放在好4后面，第一趟排序结束，前两个是数字被排好。
（14，15）92，65，35，89，79，32
第二趟排序92与15比较，比15大故放在15后面，因为92前面的数字已为升序，故92不用和14比较，因此第二趟排序为
（14，15，92）65，35，89，79，32
第三趟排序65与92比较，比92小，再与15比较比15大，故65插在15与92中间
（14，15，65，92）35，89，79，32
…
直到第七趟排序后序列为升序。
第一趟排序后（14，15）92，65，35，89，79，32
第二趟排序后（14，15，92）65，35，89，79，32
第三趟排序后（14，15，65，92）35，89，79，32
第四趟排序后（14，15，35，65，92）89，79，32
第五趟排序后（14，15，35，65，89，92）79，32
第六趟排序后（14，15，35，65，79，89，92）32
第七趟排序后（14，15，32，35，65，79，89，92）

3.代码实现

#include<stdio.h>
int main(){
    int a[8]={14,15,92,65,35,89,79,32};//定义并初始化数组
    int i,j,temp;//定义整型变量
    for(i=1;i<8;i++){    //外循环

        temp=a[i];//存放a【i】的临时变量

        for(j=i-1;j>=0;j--){//内循环

            if(temp<a[j]){  
              a[j+1]=a[j];
            }
            else{
                break;
            }

        a[j]=temp;

        }

    }
    printf("排序前的的序列为：\n");
    printf("14 15 92 65 35 89 79 32\n");
    printf("排序后的序列为：\n");
    for(i=0;i<8;i++)
        printf("%d ",a[i]);
    printf("\n");
    return 0;
}

4.运行结果展示

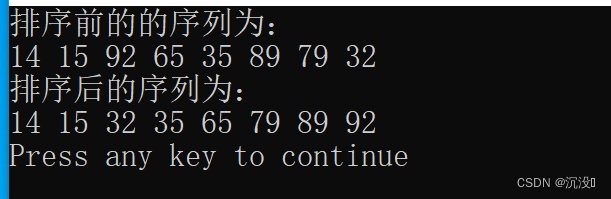
5.视频讲解

学益得智能硬件的直接插入排序

五、时间复杂度与空间复杂度分析

1.时间复杂度

1）实现内部排序的基本操作有两个：
“比较”序列中两个关键字的大小和“移动”记录
2）最好的情况序列正好是升序
比较次数：n-1 移动次数：0
最坏的情况序列正好是降序
比较次数：**(n+2)(n-1)/2** 移动次数：**(n+4)(n-1)/2**
时间复杂度为：O(n2)

2.空间复杂度

空间复杂度为：O(1)

六、说明

21天学习挑战赛打卡第二篇，自知知识水平有限，如有不当之处还望批评斧正。
参考文章一头小山猪的一文学懂经典算法系列之：直接插入排序（附讲解视频）

​