1. 相关背景
在许多领域的研究与应用中,通常需要对含有多个变量的数据进行观测,收集大量数据后进行分析寻找规律。多变量大数据集无疑会为研究和应用提供丰富的信息,但是也在一定程度上增加了数据采集的工作量。更重要的是在很多情形下,许多变量之间可能存在相关性,从而增加了问题分析的复杂性。如果分别对每个指标进行分析,分析往往是孤立的,不能完全利用数据中的信息,因此盲目减少指标会损失很多有用的信息,从而产生错误的结论。
因此需要找到一种合理的方法,在减少需要分析的指标同时,尽量减少原指标包含信息的损失,以达到对所收集数据进行全面分析的目的。由于各变量之间存在一定的相关关系,因此可以考虑将关系紧密的变量变成尽可能少的新变量,使这些新变量是两两不相关的,那么就可以用较少的综合指标分别代表存在于各个变量中的各类信息。主成分分析与因子分析就属于这类降维算法。
2. 数据降维
降维就是一种对高维度特征数据预处理方法。降维是将高维度的数据保留下最重要的一些特征,去除噪声和不重要的特征,从而实现提升数据处理速度的目的。在实际的生产和应用中,降维在一定的信息损失范围内,可以为我们节省大量的时间和成本。降维也成为应用非常广泛的数据预处理方法。
降维具有如下一些优点:
- 使得数据集更易使用。
- 降低算法的计算开销。
- 去除噪声。
- 使得结果容易理解。
降维的算法有很多,比如奇异值分解(SVD)、主成分分析(PCA)、因子分析(FA)、独立成分分析(ICA)。
3. 主成分分析(PCA)降维
PCA的主要目标是将特征维度变小,同时尽量减少信息损失。就是对一个样本矩阵,一是换特征,找一组新的特征来重新表示;二是减少特征,新特征的数目要远小于原特征的数目。
通过PCA将n维原始特征映射到维(k<n)上,称这k维特征为主成分。需要强调的是,不是简单地从n 维特征中去除其余n- k维特征,而是重新构造出全新的k维正交特征,且新生成的k维数据尽可能多地包含原来n维数据的信息。例如,使用PCA将20个相关的特征转化为5个无关的新特征,并且尽可能保留原始数据集的信息。
怎么找到新的维度呢?实质是数据间的方差够大,通俗地说,就是能够使数据到了新的维度基变换下,坐标点足够分散,数据间各有区分。
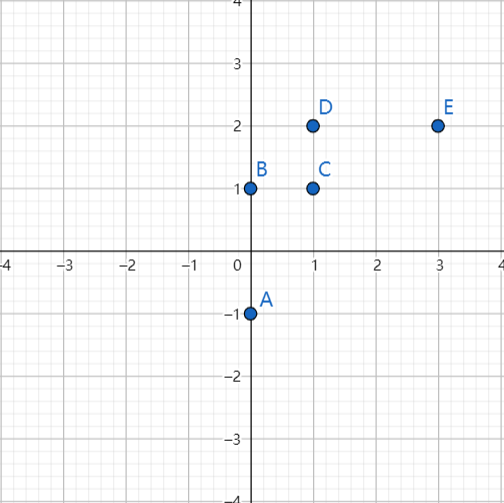
上图所示的左图中有5个离散点,降低维度,就是需要把点映射成一条线。将其映射到右图中黑色虚线上则样本变化最大,且坐标点更分散,这条黑色虚线就是第一主成分的投影方向。
PCA是一种线性降维方法,即通过某个投影矩阵将高维空间中的原始样本点线性投影到低维空间,以达到降维的目的,线性投影就是通过矩阵变换的方式把数据映射到最合适的方向。
降维的几何意义可以理解为旋转坐标系,取前k个轴作为新特征。
降维的代数意义可以理解为阶的原始样本X,与
阶的矩阵W做矩阵乘法运算
(下面简记为
),即得到
阶的低维矩阵Y,这里
阶的矩阵W就是投影矩阵。
本次介绍从最大方差理论(最大可分性)的角度理解PCA的原理。最大方差理论主要是指投影后的样本点在投影超平面上尺量分开,即投影方差最大。其中涉及的概念如下。
4. PCA 涉及的主要问题
(1)对实对称方阵,可以正交对角化,分解为特征向量和特征值,不同特征值对应的特征向量之间止交,即线性无关。特征值表示对应的特征向量的重要程度,特征值越大,代表包含的信息量越多,特征值越小,说明其信息量越少。在等式中v为特征向量,为特征值。
(2)方差相当于特征的辨识度,其值越大越好。方差很小,则意味着该特征的取值大部分相同,即该特征不带有效信息,没有区分度;方差很大,则意味着该特征带有大量信息,有区分度。
(3)协方差表示不同特征之间的相关程序,例如,考察特征x和y的协方差,如果是正值,则表明x和y正相关,即x和y的变化趋势相同,越大y越大;如果是负值,则表明x和y负相关,即x和y的变化趋势相反,x越小y越大;如果是零,则表明x和y没有关系,是相互独立的。
为计算方便,将特征去均值,设特征x的均值为,去均值后的方差为S,特征x和特征y的协方差为,设样本数为m,对应的公式分别为:

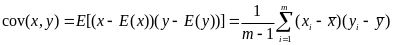
当时,表示特征x和y完全独立。
当有n个特征时,引用协方差矩阵表示多个特征之间的相关性,例如,有3个特征x、y、z,协方差矩阵为:
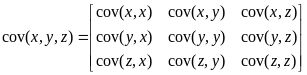
显然,协方差矩阵是实对称矩阵,其主对角线是各个特征的方差,非对角线是特征间的协方差,根据线性代数的原理,该协方差矩阵可以正交对角化,即可以分解为特征向量和特征值,特征向量之间线性无关,特征值为正数。
5. PCA 的优化目标
5.1. 构造彼此线性无关的新特征。
PCA的目标之一是新特征之间线性无关,即新特征之间的协方差为0。其实质是让新特征的协方差矩阵为对角矩阵,对角线为新特征的方差,非对角线元素为0,用来表示新特征之间的协方差0,对应的特征向量正交。
基于此目标,求解投影矩阵,具体过程如下。
不考虑降维,即维度不改变的情况下,设原始矩阵X为m个样本,n维特征,转换后的新矩阵Y仍为m个样本,n维特征。
首先对X和Y去均值化,为了简便,仍用X和Y分别表示均值化的矩阵,此时X的协方差矩阵为
 ,Y的协方差矩阵为
,Y的协方差矩阵为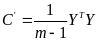 。
。
接着,将阶矩阵X变为
阶矩阵Y,最简单的是对原始数据进行线性变换:
,其中为W投影矩阵,是一组按行组成的
矩阵。将公式代人后可得:
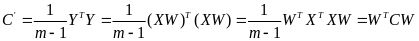
PCA的目标之一是新特征之间的协方差为0.即C为对角矩阵,根据C的计算公式可知,PCA的目标就转换为:计算出W,且W应使得 是一个对角矩阵。因为C是一个实对称矩阵,所以可以进行特征分解,所求的W即特征向量
是一个对角矩阵。因为C是一个实对称矩阵,所以可以进行特征分解,所求的W即特征向量
5.2. 选取新特征
PCA的目标之二是使最终保留的主成分,即k个新特征具有最大差异性。鉴于方差表示信息量的大小,可以将协方差矩阵C的特征值(方差)从大到小排列,并从中选取k个特征,然后将所对应的特征向量组成阶矩阵W,计算出
,作为降维后的数据,此时n维数据降低到了k维。
一般而言,k值的选取有两种方法。
①预先设立一个國值,例如0.95,然后选取使下式成立的最小k值:
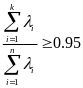
(代表特征值)
②通过交叉验证的方式选择较好的k值,即降维后机器学习模型的性能比较好。
6. PCA 求解步骤
输入:m条样本,特征数为n的数据集,即样本数据 ,降维到的目标维数为k。记样本集为矩阵X。
,降维到的目标维数为k。记样本集为矩阵X。
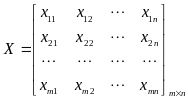
其中每一行代表一个样本,每一列代表一个特征,列号表示特征的维度,共n维。
输出:降维后的样本集
步骤如下:
第一步:对矩阵去中心化得到新矩阵X,即每一列进行零均值化,也即减去这一列的均值,
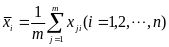 ,所求X仍为
,所求X仍为阶矩阵。
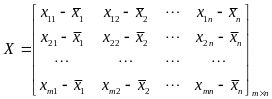
第二步:计算去中心化的矩阵X的协方差矩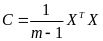 ,即阶
,即阶矩阵。
第三步:对协方差矩阵C进行特征分解,求出协方差矩阵的特征值,及对应的特征向量
,即
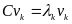
第四步:将特征向量按对应特征值从左到右按列降序排列成矩阵,取前k列组成矩阵W,即阶矩阵。
第五步,通过计算降维到k维后的样本特征,即
阶矩阵。
7.** 开源库中的PCA**
7.1. Python开源库sklearn
7.1.1. PCA模块
from sklearn.decomposition import PCA
sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False)
7.1.2. PCA属性
- **components_ **:返回具有最大方差的成分。
- singular_values_:奇异值。
- **explained_variance_ratio_**:返回 所保留的n个成分各自的方差百分比。
- **n_components_**:返回所保留的成分个数n。
7.1.3. PCA方法
- fit(X,y=None)
fit(X),表示用数据X来训练PCA模型。
函数返回值:调用fit方法的对象本身。比如pca.fit(X),表示用X对pca这个对象进行训练。
拓展:fit()可以说是scikit-learn中通用的方法,每个需要训练的算法都会有fit()方法,它其实就是算法中的“训练”这一步骤。因为PCA是无监督学习算法,此处y自然等于None。
- fit_transform(X)
用X来训练PCA模型,同时返回降维后的数据。
newX=pca.fit_transform(X),newX就是降维后的数据。
- inverse_transform()
将降维后的数据转换成原始数据,X=pca.inverse_transform(newX)
- transform(X)
将数据X转换成降维后的数据。当模型训练好后,对于新输入的数据,都可以用transform方法来降维。
7.1.4. 示例
import numpy as np
from sklearn.decomposition import PCA
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
pca = PCA(n_components=2)
newX = pca.fit_transform(X) #等价于pca.fit(X) pca.transform(X)
invX = pca.inverse_transform(newX) #将降维后的数据转换成原始数据
print(X)
[[-1 -1]
[-2 -1]
[-3 -2]
[ 1 1]
[ 2 1]
[ 3 2]]
print(newX)
array([[ 1.38340578, 0.2935787 ],
[ 2.22189802, -0.25133484],
[ 3.6053038 , 0.04224385],
[-1.38340578, -0.2935787 ],
[-2.22189802, 0.25133484],
[-3.6053038 , -0.04224385]])
print(invX)
[[-1 -1]
[-2 -1]
[-3 -2]
[ 1 1]
[ 2 1]
[ 3 2]]
print(pca.explained_variance_ratio_)
[ 0.99244289 0.00755711]
7.2. C++开源库OpenCV
7.2.1. PCA模块
#include <opencv2/opencv.hpp>
PCA pca(before_PCA, Mat(), CV_PCA_DATA_AS_ROW, 128);
7.2.2. 主要函数
C++: PCA::PCA(InputArray data, InputArray mean, int flags, int maxComponents=0)
参数依次为:原始数据;原始数据均值,输入空会自己计算;每行/列代表一个样本;保留多少特征值,默认全保留
C++: PCA::PCA(InputArray data, InputArray mean, int flags, double retainedVariance)
参数依次为:原始数据;原始数据均值,输入空会自己计算;每行/列代表一个样本;保留多少特征值,百分比,默认全保留
C++: PCA& PCA::computeVar(InputArray data, InputArray mean, int flags, double retainedVariance)
参数依次为:原始数据;原始数据均值,输入空会自己计算;每行/列代表一个样本;保留多少特征值,百分比,默认全保留
C++: Mat PCA::project(InputArray vec) const
原图像,投影到新的空间
C++: Mat PCA::backProject(InputArray vec) const
先进行project之后的数据,反映摄到原始图像
7.2.2. 成员变量
mean--------原始数据的均值
eigenvalues--------协方差矩阵的特征值
eigenvectors--------特征向量
7.2.3. 示例
#pragma once#pragma execution_character_set("utf-8")
#include <opencv/cv.h>
#include <opencv/highgui.h>
#include <stdio.h>
#include <stdlib.h>
using namespace cv;
using namespace std;
#define DIMENTIONS 7
#define SAMPLE_NUM 31
float Coordinates[DIMENTIONS*SAMPLE_NUM] = {
101.5, 100.4, 97.0, 98.7, 100.8, 114.2, 104.2
, 100.8, 93.5, 95.9, 100.7, 106.7, 104.3, 106.4
, 100.8, 97.4, 98.2, 98.2, 99.5, 103.6, 102.4
, 99.4, 96.0, 98.2, 97.8, 99.1, 98.3, 104.3
, 101.8, 97.7, 99.0, 98.1, 98.4, 102.0, 103.7
, 101.8, 96.8, 96.4, 92.7, 99.6, 101.3, 103.4
, 101.3, 98.2, 99.4, 103.7, 98.7, 101.4, 105.3
, 101.9, 100.0, 98.4, 96.9, 102.7, 100.3, 102.3
, 100.3, 98.9, 97.2, 97.4, 98.1, 102.1, 102.3
, 99.3, 97.7, 97.6, 101.1, 96.8, 110.1, 100.4
, 98.7, 98.4, 97.0, 99.6, 95.6, 107.2, 99.8
, 99.7, 97.7, 98.0, 99.3, 97.3, 104.1, 102.7
, 97.6, 96.5, 97.6, 102.5, 97.2, 100.6, 99.9
, 98.0, 98.4, 97.1, 100.5, 101.4, 103.0, 99.9
, 101.1, 98.6, 98.7, 102.4, 96.9, 108.2, 101.7
, 100.4, 98.6, 98.0, 100.7, 99.4, 102.4, 103.3
, 99.3, 96.9, 94.0, 98.1, 99.7, 109.7, 99.2
, 98.6, 97.4, 96.4, 99.8, 97.4, 102.1, 100.0
, 98.2, 98.2, 99.4, 99.3, 99.7, 101.5, 99.9
, 98.5, 96.3, 97.0, 97.7, 98.7, 112.6, 100.4
, 98.4, 99.2, 98.1, 100.2, 98.0, 98.2, 97.8
, 99.2, 97.4, 95.7, 98.9, 102.4, 114.8, 102.6
, 101.3, 97.9, 99.2, 98.8, 105.4, 111.9, 99.9
, 98.5, 97.8, 94.6, 102.4, 107.0, 115.0, 99.5
, 98.3, 96.3, 98.5, 106.2, 92.5, 98.6, 101.6
, 99.3, 101.1, 99.4, 100.1, 103.6, 98.7, 101.3
, 99.2, 97.3, 96.2, 99.7, 98.2, 112.6, 100.5
, 100.0, 99.9, 98.2, 98.3, 103.6, 123.2, 102.8
, 102.2, 99.4, 96.2, 98.6, 102.4, 115.3, 101.2
, 100.1, 98.7, 97.4, 99.8, 100.6, 112.4, 102.5
, 104.3, 98.7, 100.2, 116.1, 105.2, 101.6, 102.6
};
float Coordinates_test[DIMENTIONS] = {
104.3, 98.7, 100.2, 116.1, 105.2, 101.6, 102.6
};
int main()
{
Mat pcaSet(SAMPLE_NUM, DIMENTIONS, CV_32FC1); //原始数据
for (int i = 0; i < SAMPLE_NUM;i++)
{
for (int j = 0; j < DIMENTIONS;j++)
{
pcaSet.at<float>(i, j) = Coordinates[i*j + j];
}
}
PCA pca(pcaSet,Mat(),CV_PCA_DATA_AS_ROW);
cout << pca.mean;//均值
cout << endl;
cout << pca.eigenvalues << endl;//特征值
cout << endl;
cout << pca.eigenvectors << endl;//特征向量
Mat dst = pca.project(pcaSet);//映射新空间
cout << endl;
cout << dst;
Mat src = pca.backProject(dst);//反映射回来
cout << endl;
cout << src;
}
参考文献
主成分分析(PCA)原理详解 - 知乎
主成分分析(PCA)原理详解
【python】sklearn中PCA的使用方法_我从崖边跌落的博客-CSDN博客_sklearn pca
opencv中PCA降维_叶子的技术博客_51CTO博客
版权归原作者 瞻邈 所有, 如有侵权,请联系我们删除。