这是机器未来的第43篇文章
原文首发地址:https://blog.csdn.net/RobotFutures/article/details/126493989

文章目录
1. 概述
本文总结了numpy常见的运算,四则运算与矩阵运算,以及它们的区别。同时描述了在形状不满足要求时,在特定情况下仍然可以运算的广播机制。
2. 四则运算
四则运算即是小学时学过的+、-、*、/,在numpy中ndarray数组对象怎么进行四则运算呢?
四则运算都是对位运算,数学公式如下:
# 生成2个3*3数组import numpy as np
a = np.random.randint(low=1,high=100,size=(3,3))
b = np.random.randint(low=1,high=100,size=(3,3))print(f"a:\n{a}, type:{type(a)}")print(f"b:\n{b}")
a:
[[84 16 27]
[39 33 87]
[82 16 37]], type:<class 'numpy.ndarray'>
b:
[[68 33 96]
[92 43 69]
[14 4 88]]
2.1 加法
s
u
m
=
∑
i
,
j
M
,
N
(
a
i
j
+
b
i
j
)
sum = \sum_{i, j}^{M,N}(a_{ij}+b_{ij})
sum=i,j∑M,N(aij+bij)
# 加法sum= a + b
print(f"sum:\n{sum}")
sum:
[[128 154 172]
[ 79 133 16]
[ 96 39 115]]
2.2 减法
d
i
f
f
=
∑
i
,
j
M
,
N
(
a
i
j
−
b
i
j
)
diff = \sum_{i, j}^{M,N}(a_{ij}-b_{ij})
diff=i,j∑M,N(aij−bij)
# 减法
diff = a - b
print(f"diff:\n{diff}")
diff:
[[-30 2 -26]
[ 13 1 -6]
[-18 -3 21]]
2.3 乘法
p
r
o
d
u
c
t
=
∑
i
,
j
M
,
N
(
a
i
j
∗
b
i
j
)
product = \sum_{i, j}^{M,N}(a_{ij}*b_{ij})
product=i,j∑M,N(aij∗bij)
# 乘法
product = a * b
print(f"product:\n{product}")
product:
[[3871 5928 7227]
[1518 4422 55]
[2223 378 3196]]
2.4 除法
q
u
o
t
i
e
n
t
=
∑
i
,
j
M
,
N
(
a
i
j
/
b
i
j
)
quotient = \sum_{i, j}^{M,N}(a_{ij}/b_{ij})
quotient=i,j∑M,N(aij/bij)
# 除法
quotient = a / b
print(f"quotient:\n{quotient}")
quotient:
[[0.62025316 1.02631579 0.73737374]
[1.39393939 1.01515152 0.45454545]
[0.68421053 0.85714286 1.44680851]]
3. 矩阵运算
上面描述了ndarray数组对象的四则运算,如何利用numpy进行矩阵运算呢?
矩阵运算基本运算为加、减、乘法及数乘。
矩阵的加法、减法运算和数组的加法、减法运算一样,都是对位运算,数乘运算也比较简单,就是每个元素都乘以数,但是矩阵乘法和数组的乘法差距较大。
假设有两个矩阵, mxn矩阵A和nxs矩阵B, 两个矩阵矩阵相乘后结果为mxs矩阵。
矩阵A的列和矩阵B的行必须相等,才可以进行矩阵运算。
假设矩阵A为43的矩阵,矩阵B为32的矩阵
矩阵A:
[
a
0
,
0
a
0
,
1
a
0
,
2
a
1
,
0
a
1
,
1
a
1
,
2
a
2
,
0
a
2
,
1
a
2
,
2
a
3
,
0
a
3
,
1
a
3
,
2
]
\begin{bmatrix} a_{0,0} & a_{0,1} & a_{0,2} \\ a_{1,0} & a_{1,1} & a_{1,2} \\ a_{2,0} & a_{2,1} & a_{2,2} \\ a_{3,0} & a_{3,1} & a_{3,2} \end{bmatrix}
⎣⎡a0,0a1,0a2,0a3,0a0,1a1,1a2,1a3,1a0,2a1,2a2,2a3,2⎦⎤
矩阵B:
[
b
0
,
0
b
0
,
1
b
1
,
0
b
1
,
1
b
2
,
0
b
2
,
1
]
\begin{bmatrix} b_{0,0} & b_{0,1} \\ b_{1,0} & b_{1,1} \\ b_{2,0} & b_{2,1} \\ \end{bmatrix}
⎣⎡b0,0b1,0b2,0b0,1b1,1b2,1⎦⎤
矩阵A乘以矩阵B的结果4*2的矩阵:
[
a
0
,
0
∗
b
0
,
0
+
a
0
,
1
∗
b
1
,
0
+
a
0
,
2
∗
b
2
,
0
a
0
,
0
∗
b
0
,
1
+
a
0
,
1
∗
b
1
,
1
+
a
0
,
2
∗
b
2
,
1
a
1
,
0
∗
b
0
,
0
+
a
1
,
1
∗
b
1
,
0
+
a
1
,
2
∗
b
2
,
0
a
1
,
0
∗
b
0
,
1
+
a
1
,
1
∗
b
1
,
1
+
a
1
,
2
∗
b
2
,
1
a
2
,
0
∗
b
0
,
0
+
a
2
,
1
∗
b
1
,
0
+
a
2
,
2
∗
b
2
,
0
a
2
,
0
∗
b
0
,
1
+
a
2
,
1
∗
b
1
,
1
+
a
2
,
2
∗
b
2
,
1
a
3
,
0
∗
b
0
,
0
+
a
3
,
1
∗
b
1
,
0
+
a
3
,
2
∗
b
2
,
0
a
3
,
0
∗
b
0
,
1
+
a
3
,
1
∗
b
1
,
1
+
a
3
,
2
∗
b
2
,
1
]
\begin{bmatrix} a_{0,0}*b_{0,0}+a_{0,1}*b_{1,0}+a_{0,2}*b_{2,0} & a_{0,0}*b_{0, 1}+a_{0,1}*b_{1,1}+ a_{0,2} *b_{2,1}\\ a_{1,0}*b_{0,0}+a_{1,1}*b_{1,0}+a_{1,2}*b_{2,0} & a_{1,0}*b_{0, 1}+a_{1,1}*b_{1,1}+ a_{1,2} *b_{2,1}\\ a_{2,0}*b_{0,0}+a_{2,1}*b_{1,0}+a_{2,2}*b_{2,0} & a_{2,0}*b_{0, 1}+a_{2,1}*b_{1,1}+ a_{2,2} *b_{2,1}\\ a_{3,0}*b_{0,0}+a_{3,1}*b_{1,0}+a_{3,2}*b_{2,0} & a_{3,0}*b_{0, 1}+a_{3,1}*b_{1,1}+ a_{3,2} *b_{2,1}\\ \end{bmatrix}
⎣⎡a0,0∗b0,0+a0,1∗b1,0+a0,2∗b2,0a1,0∗b0,0+a1,1∗b1,0+a1,2∗b2,0a2,0∗b0,0+a2,1∗b1,0+a2,2∗b2,0a3,0∗b0,0+a3,1∗b1,0+a3,2∗b2,0a0,0∗b0,1+a0,1∗b1,1+a0,2∗b2,1a1,0∗b0,1+a1,1∗b1,1+a1,2∗b2,1a2,0∗b0,1+a2,1∗b1,1+a2,2∗b2,1a3,0∗b0,1+a3,1∗b1,1+a3,2∗b2,1⎦⎤
矩阵相乘的计算过程为:
矩阵A和第k行和矩阵B的第k列相乘,矩阵A的第k行第i列的元素乘以矩阵B第j列第i行的元素,然后它们的乘积再想加就是结果的第ij元素。
C
i
,
j
=
a
i
,
0
∗
b
0
,
j
+
a
i
,
1
∗
b
1
,
j
+
.
.
.
+
a
i
,
n
∗
b
n
,
j
=
∑
k
=
0
n
a
i
k
b
k
j
C_{i,j} = a_{i,0}*b_{0,j}+a_{i,1}*b_{1,j}+...+a_{i,n}*b_{n,j} = \sum_{k=0}^{n}a_{ik}b_{kj}
Ci,j=ai,0∗b0,j+ai,1∗b1,j+...+ai,n∗bn,j=k=0∑naikbkj
numpy中计算矩阵乘法的方式有4种:
3.1 np.dot函数
arr_a = np.array([[1,2,3],[4,5,6],[7,8,9],[1,2,3]])
arr_b = np.array([[1,1],[2,2],[3,3]])print(f"arr_a:{arr_a.shape},{type(arr_a)}\n{arr_a}")print(f"arr_b:{arr_b.shape},{type(arr_b)}\n{arr_b}")
matrix_c = np.dot(arr_a, arr_b)print(f"matrix_c:{matrix_c.shape},{type(matrix_c)}\n{matrix_c}")
arr_a:(4, 3),<class 'numpy.ndarray'>
[[1 2 3]
[4 5 6]
[7 8 9]
[1 2 3]]
arr_b:(3, 2),<class 'numpy.ndarray'>
[[1 1]
[2 2]
[3 3]]
matrix_c:(4, 2),<class 'numpy.ndarray'>
[[14 14]
[32 32]
[50 50]
[14 14]]
3.2 np.matmul函数
从numpy1.10.0开始支持。
arr_a = np.array([[1,2,3],[4,5,6],[7,8,9],[1,2,3]])
arr_b = np.array([[1,1],[2,2],[3,3]])print(f"arr_a:{arr_a.shape},{type(arr_a)}\n{arr_a}")print(f"arr_b:{arr_b.shape},{type(arr_b)}\n{arr_b}")
matrix_c = np.matmul(arr_a, arr_b)print(f"matrix_c:{matrix_c.shape},{type(matrix_c)}\n{matrix_c}")
arr_a:(4, 3),<class 'numpy.ndarray'>
[[1 2 3]
[4 5 6]
[7 8 9]
[1 2 3]]
arr_b:(3, 2),<class 'numpy.ndarray'>
[[1 1]
[2 2]
[3 3]]
matrix_c:(4, 2),<class 'numpy.ndarray'>
[[14 14]
[32 32]
[50 50]
[14 14]]
3.3 @运算符
arr_a = np.array([[1,2,3],[4,5,6],[7,8,9],[1,2,3]])
arr_b = np.array([[1,1],[2,2],[3,3]])print(f"arr_a:{arr_a.shape},{type(arr_a)}\n{arr_a}")print(f"arr_b:{arr_b.shape},{type(arr_b)}\n{arr_b}")
matrix_c = arr_a @ arr_b
print(f"matrix_c:{matrix_c.shape},{type(matrix_c)}\n{matrix_c}")
arr_a:(4, 3),<class 'numpy.ndarray'>
[[1 2 3]
[4 5 6]
[7 8 9]
[1 2 3]]
arr_b:(3, 2),<class 'numpy.ndarray'>
[[1 1]
[2 2]
[3 3]]
matrix_c:(4, 2),<class 'numpy.ndarray'>
[[14 14]
[32 32]
[50 50]
[14 14]]
3.4 转换为矩阵,再运算
利用np.asmatrix方法
arr_a = np.array([[1,2,3],[4,5,6],[7,8,9],[1,2,3]])
arr_b = np.array([[1,1],[2,2],[3,3]])print(f"arr_a:{arr_a.shape},{type(arr_a)}\n{arr_a}")print(f"arr_b:{arr_b.shape},{type(arr_b)}\n{arr_b}")# np.matrix方法已不推荐使用,将来会移除,asmatrix不会拷贝副本
matrix_c = np.asmatrix(arr_a)* np.asmatrix(arr_b)print(f"matrix_c:{matrix_c.shape},{type(matrix_c)}\n{matrix_c}")
arr_a:(4, 3),<class 'numpy.ndarray'>
[[1 2 3]
[4 5 6]
[7 8 9]
[1 2 3]]
arr_b:(3, 2),<class 'numpy.ndarray'>
[[1 1]
[2 2]
[3 3]]
matrix_c:(4, 2),<class 'numpy.matrix'>
[[14 14]
[32 32]
[50 50]
[14 14]]
4. numpy的广播机制
Numpy的四则运算在计算时必须满足形状一致,而Numpy的广播机制在满足广播条件约束的情况,可以将不同形状的数组扩展成统一的形状,然后再进行运算。
一般广播规则
当对两个数组进行操作时,NumPy 会逐元素比较它们的形状。 它从尾随(即最右边)维度开始,从右向左比较,
(1)维度不相等,两个数组的右侧轴元素个数相符
(2)维度相等,且其中之一的轴的元素个数为1,且其它轴的元素个数相等
(3)维度不相等,两个数组的右侧元素个数不相符,且一侧元素个数为1,则按照两侧元素个数多的为标准进行广播
则满足广播机制。
4.1 举例1
数组a,其形状为43,数组b,其形状为3,从尾部开始比较,数组a的形状43包含数组b的形状3,因此满足广播机制。
import numpy as np
a = np.array([[0.0,0.0,0.0],[10.0,10.0,10.0],[20.0,20.0,20.0],[30.0,30.0,30.0]])
b = np.array([1.0,2.0,3.0])
c = a + b
print(a.shape, b.shape, c.shape)print(c)
(4, 3) (3,) (4, 3)
[[ 1. 2. 3.]
[11. 12. 13.]
[21. 22. 23.]
[31. 32. 33.]]
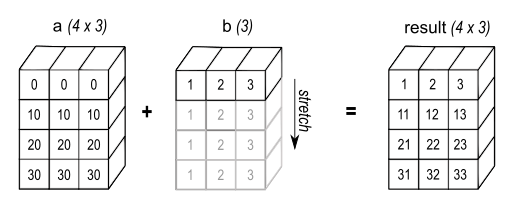
4.2 举例2
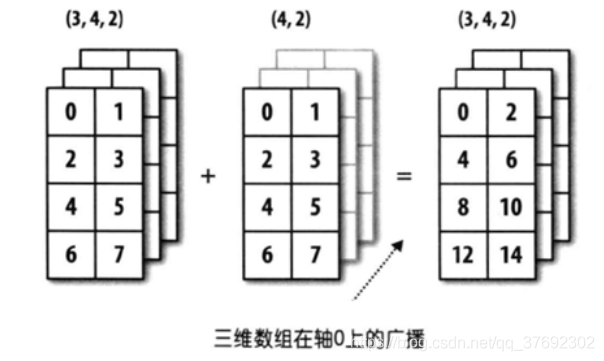
数组a,其形状为342,数组b,其形状为42,从尾部开始比较,数组a的形状342包含数组b的形状42,因此满足广播机制。
a = np.random.randint(low=0, high=10, size=(3,4,2))
b = np.random.randint(low=0, high=10, size=(4,2))
c = a + b
print(a.shape, b.shape, c.shape)print(f"a:{a}\nb:{b}\nc:{c}")
(3, 4, 2) (4, 2) (3, 4, 2)
a:[[[6 0]
[2 3]
[7 6]
[9 7]]
[[3 1]
[0 5]
[6 0]
[1 9]]
[[7 2]
[0 3]
[2 3]
[0 6]]]
b:[[7 3]
[0 5]
[6 7]
[1 7]]
c:[[[13 3]
[ 2 8]
[13 13]
[10 14]]
[[10 4]
[ 0 10]
[12 7]
[ 2 16]]
[[14 5]
[ 0 8]
[ 8 10]
[ 1 13]]]
4.3 举例3
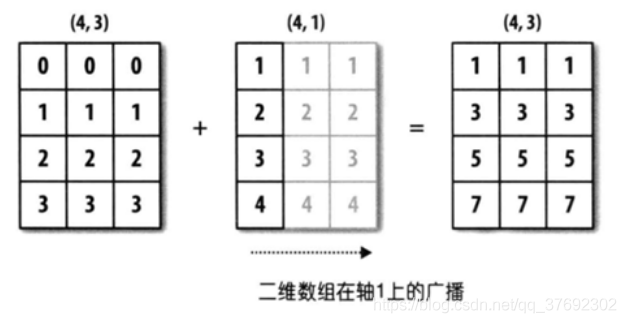
数组a形状为43,数组b形状为41,数组维度相同,有2个维度,其中一个维度元素个数为1,另外一个维度元素个数相等,满足广播机制
import numpy as np
a = np.array([[0,0,0],[1,1,1],[2,2,2],[3,3,3]])#arr1.shape = (4,3)
b = np.array([[1],[2],[3],[4]])#arr2.shape = (4, 1)
c = a + b
print(c)
[[1 1 1]
[3 3 3]
[5 5 5]
[7 7 7]]
4.4 举例4
数组a形状为(5, 4, 3),数组b形状为(5, 1, 3),数组维度相同,有3个维度,其中一个维度元素个数为1,另外2个维度元素个数相等,满足广播机制
a = np.random.randint(low=0, high=10, size=(5,4,3))
b = np.random.randint(low=0, high=10, size=(5,1,3))
c = a + b
print(a.shape, b.shape, c.shape)print(f"a:{a}\nb:{b}\nc:{c}")
(5, 4, 3) (5, 1, 3) (5, 4, 3)
a:[[[7 4 5]
[9 9 1]
[7 6 8]
[9 5 7]]
[[3 0 0]
[1 2 4]
[0 1 8]
[5 2 6]]
[[9 5 0]
[5 8 5]
[7 1 8]
[9 2 9]]
[[7 9 0]
[4 5 3]
[7 2 7]
[0 8 9]]
[[2 4 2]
[2 3 1]
[8 3 5]
[5 7 4]]]
b:[[[2 5 2]]
[[4 3 3]]
[[5 3 0]]
[[0 6 6]]
[[3 6 8]]]
c:[[[ 9 9 7]
[11 14 3]
[ 9 11 10]
[11 10 9]]
[[ 7 3 3]
[ 5 5 7]
[ 4 4 11]
[ 9 5 9]]
[[14 8 0]
[10 11 5]
[12 4 8]
[14 5 9]]
[[ 7 15 6]
[ 4 11 9]
[ 7 8 13]
[ 0 14 15]]
[[ 5 10 10]
[ 5 9 9]
[11 9 13]
[ 8 13 12]]]
4.5 举例5
数组a的形状为(3, 1, 2),数组b的形状为(4, 1),从右侧向左比较,数组a和数组b的维度不相等,右侧元素个数也不相等,但是两侧都有出现轴的元素个数为1的情况,则轴元素个数为1的维度根据两者的较大值进行广播。
从右向左比较,数据b首先在第2维上广播为(4, 2),然后数组a在第1维广播为(3, 4, 2),数组b在第0维广播为(3, 4, 2)
a = np.random.randint(low=0, high=10, size=(3,1,2))
b = np.random.randint(low=0, high=10, size=(4,1))
c = a + b
print(a.shape, b.shape, c.shape)print(f"a:{a}\nb:{b}\nc:{c}")
(3, 1, 2) (4, 1) (3, 4, 2)
a:[[[7 1]]
[[8 5]]
[[4 8]]]
b:[[2]
[0]
[7]
[0]]
c:[[[ 9 3]
[ 7 1]
[14 8]
[ 7 1]]
[[10 7]
[ 8 5]
[15 12]
[ 8 5]]
[[ 6 10]
[ 4 8]
[11 15]
[ 4 8]]]
以上就是numpy的四则运算、矩阵运算以及广播机制的作用机制了。
5. 总结
数组的四则运算
∑ i , j M , N ( a i j + ∣ − ∣ ∗ ∣ / b i j ) \sum_{i, j}^{M,N}(a_{ij} + | - | * | / b_{ij})i,j∑M,N(aij+∣−∣∗∣/bij)
矩阵相乘
C i , j = a i , 0 ∗ b 0 , j + a i , 1 ∗ b 1 , j + . . . + a i , n ∗ b n , j = ∑ k = 0 n a i k b k j C_{i,j} = a_{i,0}*b_{0,j}+a_{i,1}*b_{1,j}+...+a_{i,n}*b_{n,j} = \sum_{k=0}^{n}a_{ik}b_{kj}Ci,j=ai,0∗b0,j+ai,1∗b1,j+...+ai,n∗bn,j=k=0∑naikbkj
广播机制的三种场景- 维度不相等,两个数组的右侧轴元素个数相符- 维度相等,且其中之一的轴的元素个数为1,且其它轴的元素个数相等- 维度不相等,两个数组的右侧元素个数不相符,且一侧元素个数为1,则按照两侧元素个数多的为标准进行广播 则满足广播机制。
写在末尾:
- 博客简介:专注AIoT领域,追逐未来时代的脉搏,记录路途中的技术成长!
- 专栏简介:从0到1掌握数据科学常用库Numpy、Matploblib、Pandas。
- 面向人群:AI初级学习者
- 专栏计划:接下来会逐步发布跨入人工智能的系列博文,敬请期待 - Python零基础快速入门系列- Python数据科学系列- 人工智能开发环境搭建系列- 机器学习系列- 物体检测快速入门系列- 自动驾驶物体检测系列- …

版权归原作者 机器未来 所有, 如有侵权,请联系我们删除。