文章目录
二阶Givens旋转矩阵
在QR分解中，Givens旋转是一种用于将矩阵变成上三角形的技术。
别的教程里面往往会直接给出一个n*n阶的通用Givens矩阵形式，但是这样太过抽象难懂了，而且难以领略到Givens变换的背后内涵，四臂西瓜我在学习矩阵论的时候就深陷其害，现在我写这篇教程，就是淋过雨，要为后人撑伞！
Givens矩阵，也可以叫旋转矩阵，它实际上是通过旋转，归零矩阵中的特定元素。不好理解吧？看了下面的例子就明白了。
为了方便理解，我们先以二阶为例。
作用于向量
现在我们手上有这么一个向量：
a1=(42)a_1 = \begin{pmatrix} 4\\2\end{pmatrix}a1=(42)
现在我们想把这个向量，旋转到x轴上，变成
a1′=(r0)a_1^{'} = \begin{pmatrix} r\\0\end{pmatrix}a1′=(r0)
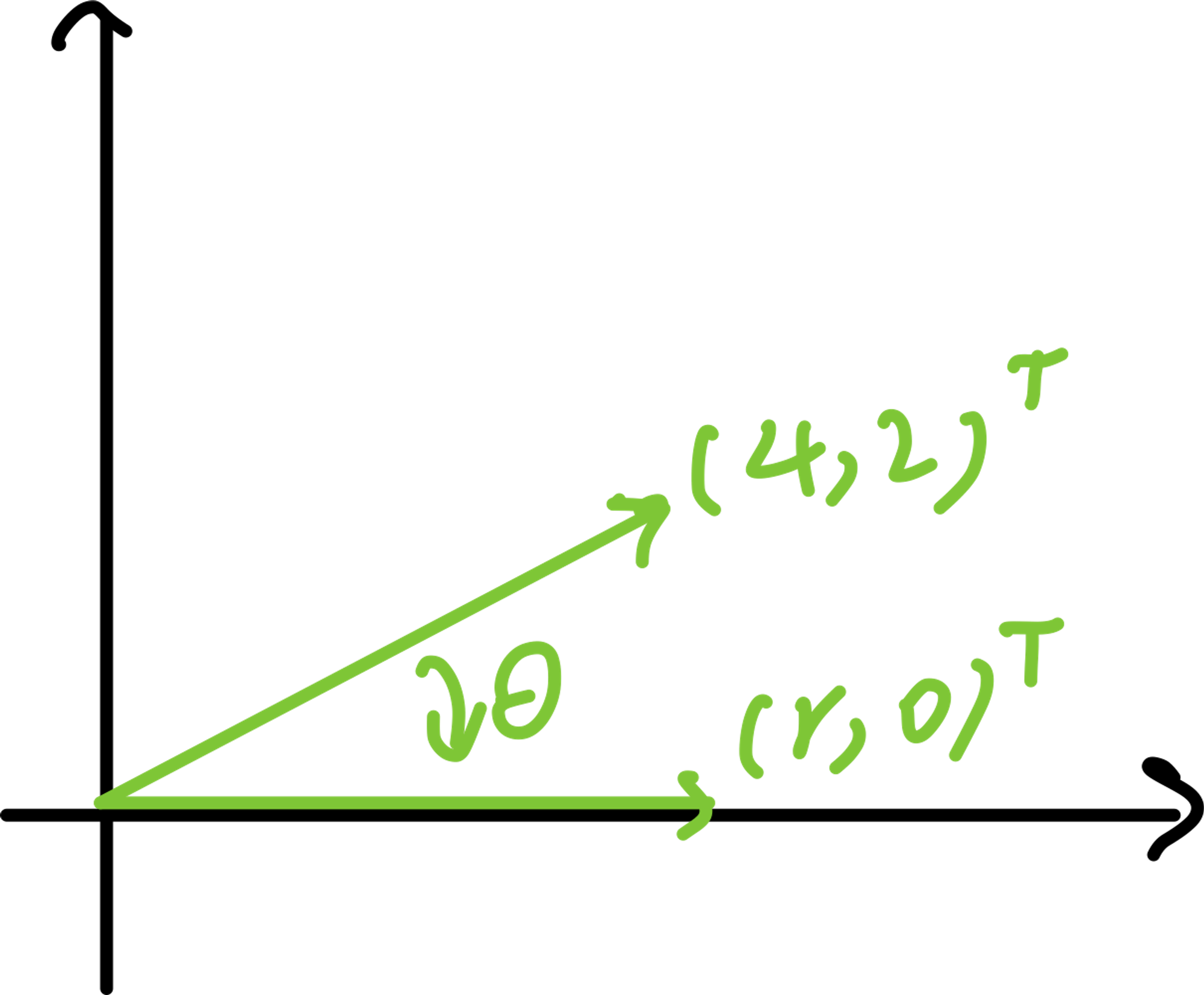
这个变换可以用如下的方式进行表示：
(cs−sc)(42)=(4c+2s−4s+2c)=(r0)=a1′\begin{pmatrix}c&s\\-s&c\end{pmatrix}\begin{pmatrix}4\\2\end{pmatrix} = \begin{pmatrix}4c+2s \\ -4s+2c \end{pmatrix}=\begin{pmatrix}r\\0\end{pmatrix}= a_1^{'}(c−ssc)(42)=(4c+2s−4s+2c)=(r0)=a1′
此处的
(cs−sc)=(cos(θ)sin(θ)−sin(θ)cos(θ))\begin{pmatrix}c&s\\-s&c\end{pmatrix} = \begin{pmatrix}\cos(\theta)&\sin(\theta)\\-\sin(\theta)&\cos(\theta)\end{pmatrix}(c−ssc)=(cos(θ)−sin(θ)sin(θ)cos(θ))表示一个标准的旋转矩阵。对应向量旋转角度$ \theta$。
于是我们可以得到下面的方程组
{4c+2s=r−4s+2c=0\left \{ \begin{matrix} 4c+2s &= r \\ -4s+2c &= 0 \end{matrix} \right.{4c+2s−4s+2c=r=0
因为是旋转变换，所以向量的模值不会改变，
r=42+22r = \sqrt{4^2+2^2}r=42+22就是这个模值{4c+2s=42+22−4s+2c=0\left \{ \begin{matrix} 4c+2s &=& \sqrt{4^2+2^2} \\ -4s+2c &=& 0 \end{matrix} \right.{4c+2s−4s+2c==42+220
可以解得
{c=242+22=220=24.4721=0.4472s=442+22=420=44.4721=0.8944\left \{ \begin{aligned}c&=\frac{2}{\sqrt{4^{2}+2^{2}}}=\frac{2}{\sqrt{20}}=\frac{2}{4.4721}=0.4472\\s&=\frac{4}{\sqrt{4^{2}+2^{2}}}=\frac{4}{\sqrt{20}}=\frac{4}{4.4721}=0.8944\end{aligned} \right.⎩⎨⎧cs=42+222=202=4.47212=0.4472=42+224=204=4.47214=0.8944
因此可以得到旋转矩阵
G=(cs−sc)=(0.44720.8944−0.89440.4472)G=\begin{pmatrix}c&s\\-s&c\end{pmatrix}=\begin{pmatrix}0.4472&0.8944\\-0.8944&0.4472\end{pmatrix}G=(c−ssc)=(0.4472−0.89440.89440.4472)
现在我们终于得到了最终的运算，成功将向量旋转到了x轴上，将y坐标清零。
G(42)=(0.44720.8944−0.89440.4472)(42)=(4.47210)G\begin{pmatrix}4\\2\end{pmatrix}=\begin{pmatrix}0.4472&0.8944\\-0.8944&0.4472\end{pmatrix}\begin{pmatrix}4\\2\end{pmatrix}=\begin{pmatrix}4.4721\\0\end{pmatrix}G(42)=(0.4472−0.89440.89440.4472)(42)=(4.47210)
作用于矩阵
理解了上述的过程后，现在我们可以看下旋转矩阵作用于矩阵的效果了。我们有如下矩阵，他左边的向量就是上一部分的
A=(4121)A=\begin{pmatrix}4&1\\2&1\end{pmatrix}A=(4211)
直接将上一节计算的旋转矩阵作用于
AAAG(4121)=(4.47211.34160−0.4472)G\begin{pmatrix}4&1\\2&1\end{pmatrix}=\begin{pmatrix}4.4721&1.3416\\0&-0.4472\end{pmatrix}G(4211)=(4.472101.3416−0.4472)
确实将A矩阵变为了上三角矩阵，实现了QR分解。其中左边的向量，正是上一节计算出来的结果。相信大家看到这里就有所领悟了。
对于矩阵，我们可以把它理解为多个列向量拼接而成。
a1=(42)a2=(11)a_1 = \begin{pmatrix} 4\\2\end{pmatrix}\\ a_2 = \begin{pmatrix} 1\\1\end{pmatrix}a1=(42)a2=(11)
那么A可以理解为他们水平拼接在一起
A=[a1∣∣a2]A = [a_1||a_2]A=[a1∣∣a2]
根据拼接的运算性质，旋转矩阵作用于A，相当于分别作用于
a1a_1a1和a2a_2a2，再将它们拼接在一起。G⋅[a1∣∣a2]=[G⋅a1∣∣G⋅a2]G\cdot[a_1||a_2]=[G\cdot a_1||G\cdot a_2]G⋅[a1∣∣a2]=[G⋅a1∣∣G⋅a2]
我们现在借助这个性质再来理解下givens作用于矩阵
G(42)=(0.44720.8944−0.89440.4472)(42)=(4.47210)G\begin{pmatrix}4\\2\end{pmatrix}=\begin{pmatrix}0.4472&0.8944\\-0.8944&0.4472\end{pmatrix}\begin{pmatrix}4\\2\end{pmatrix}=\begin{pmatrix}4.4721\\0\end{pmatrix}G(42)=(0.4472−0.89440.89440.4472)(42)=(4.47210)G(11)=(0.44720.8944−0.89440.4472)(11)=(1.3416−0.4472)G\begin{pmatrix}1\\1\end{pmatrix}=\begin{pmatrix}0.4472&0.8944\\-0.8944&0.4472\end{pmatrix}\begin{pmatrix}1\\1\end{pmatrix}=\begin{pmatrix}1.3416\\-0.4472\end{pmatrix}G(11)=(0.4472−0.89440.89440.4472)(11)=(1.3416−0.4472)
对于
a1a_1a1向量，借助旋转矩阵成功清零y坐标；对于a2a_2a2矩阵，旋转矩阵作用后，得到新的向量
这里给大家留个思考，有没有可能，
a2a_2a2矩阵，经过旋转矩阵后y轴也被清零？
G⋅[a1∣∣a2]=[G⋅a1∣∣G⋅a2]=[G(42)∣∣G(11)]=(4.47211.34160−0.4472)G\cdot[a_1||a_2]=[G\cdot a_1||G\cdot a_2] =[G\begin{pmatrix}4\\2\end{pmatrix} ||G\begin{pmatrix}1\\1\end{pmatrix}] =\begin{pmatrix}4.4721&1.3416\\0&-0.4472\end{pmatrix}G⋅[a1∣∣a2]=[G⋅a1∣∣G⋅a2]=[G(42)∣∣G(11)]=(4.472101.3416−0.4472)
现在我们来总结下上面的清空过程，我们选择第一个列向量，通过构造givens矩阵，将其第二行清零，使得矩阵整体变为上三角形式。
到这里，相信大家能够理解最一开始的那句话，givens矩阵通过旋转作用，将矩阵变化为上三角形式。
更一般的情况
我们有如下矩阵，我们希望将c的位置，清零。
A=(abcd)A=\begin{pmatrix}a&b\\c&d\end{pmatrix}A=(acbd)
构造旋转矩阵
G=(cs−sc)G=\begin{pmatrix}c&s\\-s&c\end{pmatrix}G=(c−ssc)
得到
(cs−sc)(ac)=(r0)\begin{pmatrix}c&s\\-s&c\end{pmatrix}\begin{pmatrix}a\\c\end{pmatrix}=\begin{pmatrix}r\\0\end{pmatrix}(c−ssc)(ac)=(r0)
解方程后，我们就可以得到最终的形式：
s=sin(θ)=aa2+c2c=cos(θ)=ca2+c2\begin{aligned}s=\sin(\theta)=\frac a{\sqrt{a^2+c^2}}\\c=\cos(\theta)=\frac c{\sqrt{a^2+c^2}}\end{aligned}s=sin(θ)=a2+c2ac=cos(θ)=a2+c2c
这边读者可以带入前面的二阶例子中，熟悉计算过程，加深理解。
本文转载自: https://blog.csdn.net/qq_34022877/article/details/140409133
版权归原作者 四臂西瓜 所有， 如有侵权，请联系我们删除。
版权归原作者 四臂西瓜 所有， 如有侵权，请联系我们删除。