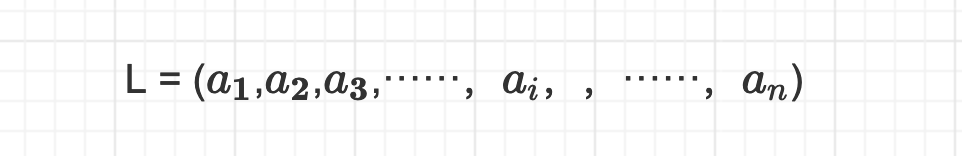🌕写在前面
Hello🤗大家好啊,我是kikokingzz,名字太长不好记,大家可以叫我kiko哦~
从今天开始,我将正式开启一个新的打卡专题——【数据结构·水滴计划】,没错!这是今年上半年的一整个系列计划!本专题目的是通过百天刷题计划,通过题目和知识点串联的方式,刷够1000道题!完成对数据结构相关知识的全方位复习和巩固;同时还配有专门的笔记总结和文档教程哦!想要搞定,搞透数据结构的同学
🎉🎉欢迎订阅本专栏🎉🎉
🍊博客主页:kikoking的江湖背景🍊
🌟🌟往期必看🌟🌟
【数据结构】第一话·数据结构入门竟如此简单?
收藏量:471
【数据结构】第二话·带你彻底吃透算法复杂度
收藏量:1517


🍺知识点3:线性表
🥝3.1 线性表的定义与操作
🍊1.什么是线性表?
线性表是一种逻辑结构,它是具有相同数据类型的n(n>=0)个数据元素的有限集合,其中n为表长,当n=0时,线性表是一个空表。若用L命名线性表,则其一般表示为:
如果采用更生动一点方式来描述线性表的话,我们可以看看下图呀:
🍊2.线性表的特点有哪些?
(1)表中元素个数有限。
(2)表中元素数据类型相同,因此每个元素占用相同大小的存储空间。
(3)表中元素具有逻辑上的顺序性,各元素之间有先后次序。
(4)表中元素具有抽象性,仅讨论元素间的逻辑关系,而不考虑元素究竟是什么内容。
注意:线性表是一种逻辑结构,表示元素间一对一的相邻关系,而顺序表和链表是存储结构。
02.以下( )是一个线性表。 A.由n个实数组成的集合 B.由100个字符组成的序列 C.所有整数组成的序列 D.邻接表kiko:A. 集合中的元素没有前后之间的逻辑关系;B. 是有限个数据元素组成的序列,序列具有逻辑关系,满足线性表的要求;C. 所有整数的个数是无限个,不满足线性表中元素个数有限的特点;D. 邻接表属于存储结构,而线性表是一种逻辑结构;因此正确答案:B
🍊3.线性表的基本操作有哪些?
一个数据结构的基本操作是指其最核心、最基本的操作。其他较复杂的操作可以通过调用这些基本操作来实现,要注意之后学习的顺序表的基本操作,就是线性表在顺序存储的情况下的一些基本操作。
- (创)初始化:构造一个空的线性表。
- (销)销毁表:销毁操作,销毁线性表,并释放线性表所占用的空间。
- (增)插入操作:在表中某位置插入指定元素。
- (删)删除操作:删除表中某位置元素。
- (查)按值查找:在表中查找具有给定关键字值的元素。
- (查)按位查找:获取表中第i个位置的元素的值。
- 输出操作:按照前后顺序输出线性表中的所有元素。
- 求表长:返回线性表的长度,即线性表中元素的个数。
- 判空操作:若为空表,返回true,否则返回false。
对于上面这些基本操作,其实我们只需要记住一个口诀,就可以将上述最重要的一些基本功能囊括其中:线性表的基本操作有:创、销、增、删、改、查。
PS:上述操作中并没有出现“改”,但是在实际执行运算过程中,“查”操作有一部分是为了“改”,比如:我需要将线性表中所有值为1的元素改为0,这时我需要先通过“按值查找”找到指定元素,然后才可以进行值的修改。

🍺知识点4:顺序表
🥝4.1 顺序表的定义与特点
🍊1.什么是顺序表?
线性表的顺序存储又称为顺序表,实际上就是一个数组;它用一组地址连续的存储单元依次存储线性表中的数据元素,从而使得逻辑上相邻的两个元素在物理位置上也相邻。第1个元素存储在线性表的起始位置,第i个元素的存储位置后面紧接着存储的是第i+1个元素,称 i 为元素
在线性表中的位序。
🍊2.顺序表的特点有哪些呢?
(1)双序相同:顺序表中元素的逻辑顺序与物理顺序相同。
(2)随机存取:当你知道数组首地址后,可以在相同时间内读取任何一个位置的元素;如上图所示,假设
的内存地址为LOC(A),那么你可以在O(1)的时间找到元素
,因为
在内存中的存储位置为**LOC(A)+(i-1)*sizeof(ElemType)**,这个计算式对所有元素都是一样的计算时间,可以理解为,访问任何一个元素的时间都是相同的,也就是随机存取。
PS:对于链表来说,假如要读取第
个,那么就需要依次从头挨个读取,一直读到第i个才能找到。
01.下述( )是顺序存储结构的优点。 A.存储密度大 B.插入运算方便 C.删除运算方便 D.方便地运用于各种逻辑结构的存储表示kiko:顺序表不像链表那样要在结点中存放指针域,因此存储密度较大,A正确。B和C是链表的优点,对于顺序表来说是缺点。D是错误的,比如对于树形结构,顺序表显然不如链表表示起来方便;因此本题选A。
04.若线性表最常用的操作是存取第i个元素及其前驱和后继元素的值,为了提高效率,应 采用( )的存储方式。 A.单链表 B.双向链表 C.单循环链表 D.顺序表kiko:题干实际要求能最快存取第i-1、i、i+1个元素值。A、B、C都只能从头结点依次顺序查找,时间复杂度为O(N),只有顺序表可以按序号随机存取,时间复杂度为O(1);因此本题选D。
02.线性表的顺序存储结构是一种( )。 A.随机存取的存储结构 B.顺序存取的存储结构 C.索引存取的存储结构 D.散列存取的存储结构kiko:本题易误选B。注意,存取方式是指读写方式。顺序表是一种支持随机存取的存储结构,根据起始地址加上元素的序号,可以很方便地访问任意--个元素,这就是随机存取的概念。
** ✨✨✨我是分割线✨✨✨**
🥝4.2 顺序表的静态分配
🍊1.什么是顺序表的静态分配?
顺序表在静态分配时,使用“静态”的数组存放数据元素。静态的意思是:数组的大小和空间是事先预定好的,因此一旦空间占满,如果出现新的数据,就会产生溢出,最终导致程序崩溃。
缺点:开小了不够用,开大了会存在浪费。
🍊2.静态顺序表的定义
Q1:定义一个静态顺序表需要哪些参数?
A1:关于这个问题很多书上都没有提及,从个人角度认为,其参数细节主要有以下几点:
- 顺序表的最大长度:通俗来说,我们得知道顺序表能存放多少个元素,对于静态顺序表来说,我们通过采用宏定义的方式确定其最多可存100个元素;
- 顺序表中元素类型:我们要知道顺序表存放的是什么类型的数据元素,下例中我们通过定义 int a[N] 确定顺序表存放的元素类型为int型,且开辟了100个空间;
- 顺序表的当前长度:我们需要知道当前顺序表已经存了多少元素,进而在一些对顺序表插入、删除等操作时,方便我们处理元素。
由于定义一个顺序表需要囊括以上三类参数,因此我们采用结构体的方式,将他们集合到一起,所以最终采用了结构体的方式。
//静态的顺序表 #define N 100 //定义顺序表的最大长度 struct SeqList { int a[N];//定义顺序表存储的元素类型和元素个数 int size;//定义顺序表的当前存储个数 };
** ✨✨✨我是分割线✨✨✨**
🥝4.3 顺序表的动态分配
🍊1.什么是顺序表的动态分配?
采用动态分配时,存储数组的空间是在程序执行过程中通过动态存储分配语句分配的,一旦数据空间占满,就另外开辟一块更大的存储空间,用以替换原来的存储空间,从而达到扩充数组空间的目的,而不需要为线性表一次性地划分所有空间。
🍊2.动态顺序表的定义
kiko:在学完静态顺序表定义的参数细节后,对于动态顺序表的定义,我希望大家可以先思考一下动态顺序表需要哪些参数,然后自己写一个结构体试试先。
Q1:定义一个动态顺序表需要哪些参数?
A1:动态与静态顺序表的唯一区别就在于,动态顺序表是可以进行动态分配,遇到扩容时,元素是可以整体“搬家”的,“搬”到新的内存地址空间去,因此我们在这里将定义动态数组的指针(注意不是定义静态数组咯!),而其余参数和静态顺序表的需求是一样的,动态顺序表同样需要知道其当前情况下的最大容量capacity和当前元素个数size。
typedef int DataType;//将int重定义为DataType //下次想更改数据类型的时候只需要更改前面的int就可以,无需改变整个程序 typedef struct SeqList //定义一个顺序表的结构体 { DataType* a;//定义指示动态分配数组的指针 DataType size;//定义数组中有效数据的个数 DataType capacity;//定义数组的容量 }SEQ;// 将SeqList这个结构体重定义为SEQ,为了后续方便写程序Q2:为什么上例要使用DataType而不直接使用int?
A2:这里使用了 typedef 将int类型重定义为 DataType 型,目前动态顺序表存储的元素类型是int型,但如果下次该表改存float型数据元素时,我们只需要将上例第一行的int改为float就可以实现存储元素类型的变换;但如果不使用DataType而是整个程序都使用int,那么修改的时候就需要修改整个程序,太麻烦了!
🍊3.动态顺序表的功能定义
下面是一个动态顺序表的一些最核心、最基本的操作。其他较复杂的操作都可以通过调用以下操作的组合来实现。动态顺序表的主要操作有:
void SeqListInit(SeqList *sl);//(1)初始化顺序表 void SeqListDestroy(SeqList* sl);//(2)销毁顺序表 void SeqListCheckCapacity(SeqList* sl);//(3)动态监测与扩容 void SeqListPushBack(SeqList* sl, DataType x);//(4)尾插 void SeqListPushFront(SeqList* sl, DataType x);//(5)头插 void SeqListInsert(SeqList* sl, size_t pos, DataType x);//(6)指定位置插入 void SeqListPopBack(SeqList* sl)//(7)尾删 void SeqListPushPop(SeqList* sl);//(8)头删 void SeqListErase(SeqList* sl, size_t pos)//(9)指定位置删除 int SeqListFind(SeqList* sl, DataType x)//(10)按值查找
✨✨✨我是分割线✨✨✨
**🥝4.4 动态分配的代码实现 **
(1)初始化顺序表·SeqListInit
初始化一个顺序表,首先需要保证传入这个动态数组的指针不为空,因此这里使用assert进行断言操作,如果传入空指针,就会进行报错。由于是初始化操作,因此将该顺序表中所有参数置0,动态数组指针置NULL。
PS:有些书籍在初始化时就为顺序表分配空间,但在本例中,将会统一在"动态监测与扩容"这一步进行,这是因为在初始化时为其分配空间的操作,也是扩容操作的一种情况,在这里我将它们集中在同一模块了。
void SeqListInit(SeqList *sl) { assert(sl);//进行断言操作,防止空指针 sl->a = NULL;//将指向动态数组的指针置为空 sl->size = 0;//表中元素个数置为0 sl->capcity = 0;//表的容量置为0 }
(2)销毁顺序表·SeqListDestroy
销毁顺序表比较简单,但是我们注意不要遗漏,我们可以从大到小进行销毁:
- step1.释放整个顺序表的空间,即释放动态数组的空间
- step2.将指向动态数组的指针置空
- step3.将数组的容量和元素个数置0
void SeqListDestroy(SeqList* sl)//销毁顺序表 { assert(sl); free(sl->a);//释放动态数组空间 sl->a = NULL;//将动态数组的头指针置空 sl->capacity = sl->size = 0;//将数组容量和元素个数置0 }
(3)动态监测与扩容·SeqCheckCapacity
该函数的主要操作是监测当前数组是否已满,如果元素已满将进行扩容操作;下例中是将数组的最大容量直接扩容2倍。
void SeqListCheckCapacity(SeqList* sl) { assert(sl);//声明sl,防止传入空指针 if (sl->size == sl->capacity)//如果相等,说明数组已满 { DataType newcapacity = sl->capacity == 0 ? 4 : sl->capacity * 2;//扩容 DataType* tmp = realloc(sl->a, sizeof(DataType) * newcapacity);//动态申请空间 if (tmp == NULL)//判断动态申请空间操作是否成功 { printf("realloc fail\n"); exit(-1); } else { sl->a = tmp;//将新申请的地址赋给动态数组指针 sl->capacity = newcapacity;//将新申请的空间赋予给capacity } } }Q1:初始化时未给动态数组分配空间,在这一步上是如何实现的?
DataType newcapacity = sl->capacity == 0 ? 4 : sl->capacity * 2;//扩容 DataType* tmp = realloc(sl->a, sizeof(DataType) * newcapacity);//动态申请空间A1:是通过上面两行程序实现的,在初始化时,我们将capacity赋值为0,因此当进入上述程序(三目操作符判断时),当capacity值为0时,将返回一个4赋值给newcapacity,相当于为其分配了4个初始空间。
番外内容:realloc的细节
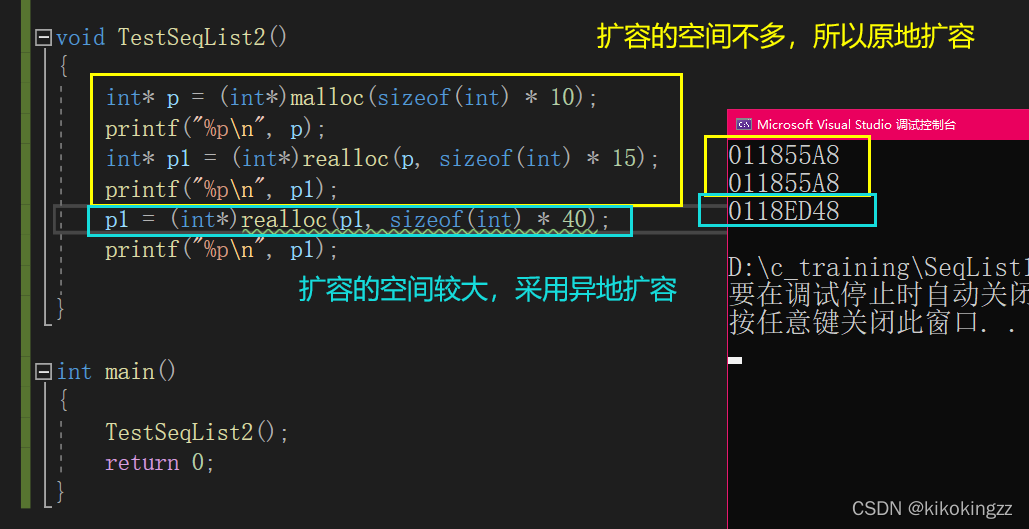
realloc可以对给定的指针所指的空间进行扩大或者缩小,无论是扩张或是缩小,原有内存的中内容将保持不变。缩小时,被缩小的那一部分的内容会丢失;扩大时,realloc试图直接在现存的数据后面获得附加空间,当数据后面的空间不足时,就会重新寻找开辟一个足够的空间,将现存数据拷贝到新地址。(更多内容详见:malloc,realloc和calloc的区别)
- 原地扩容:如果现存数据后面附加空间够用,就原地扩容。
- 异地扩容:如果现存数据后面附加空间不足,就异地扩容。
Q2:为啥上例不使用malloc呢?
A2:因为malloc是完全异地扩容,需要自己搬数据,释放旧空间,而realloc是有可能进行原地扩容的,消耗的代价可能会更低一些。
(4)尾插元素·SeqListPushBack
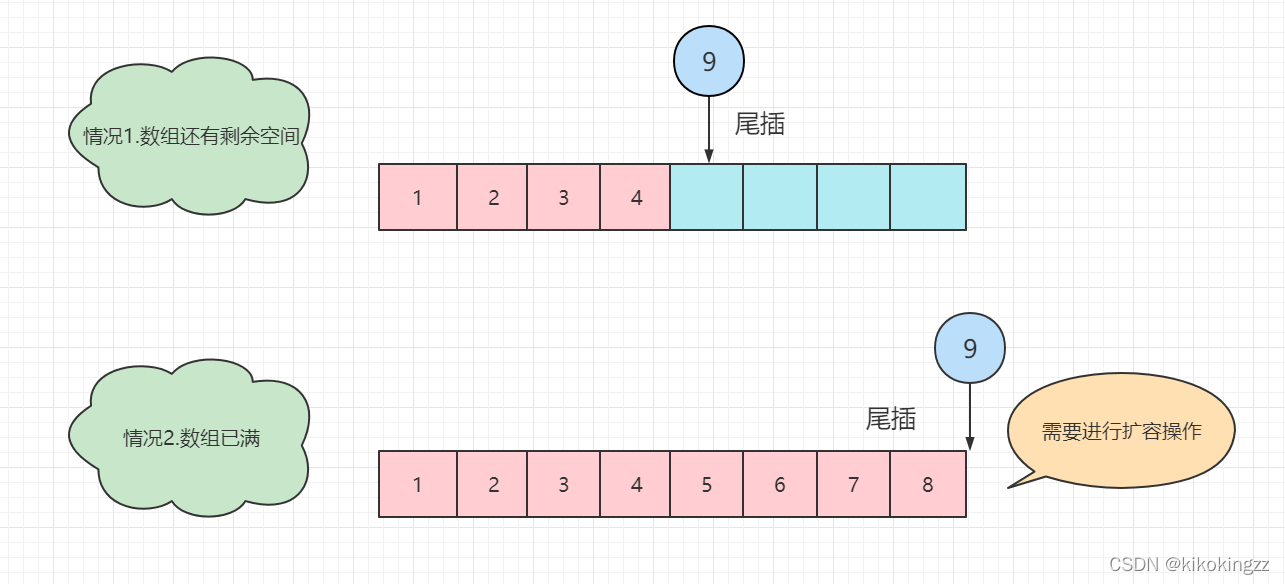
对于尾插元素,我们第一步先检测数组是否已经存满,如果存满了,我们就先对其进行扩容(使用SeqCheckCapacity来进行扩容),然后在数组尾元素后插入该元素,最后将size++即可。
时间复杂度:O(1)
void SeqListPushBack(SeqList* sl, DataType x)//尾插 { SeqListCheckCapacity(sl);//检测数组是否已满,满了就扩容 sl->a[sl->size] = x; //尾插元素x sl->size++; //表中元素个数+1 }
(5)头插元素·SeqListPushFront
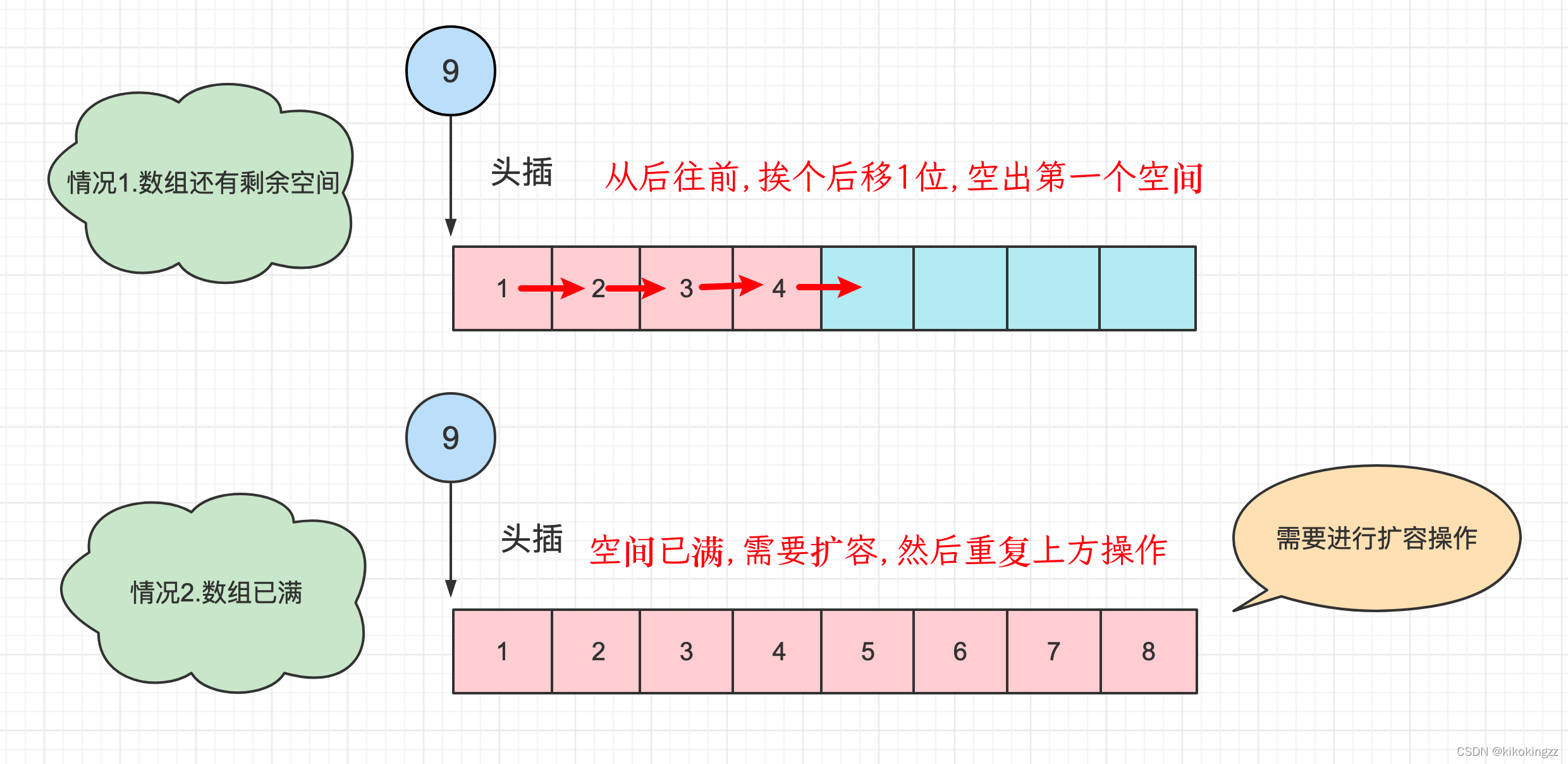
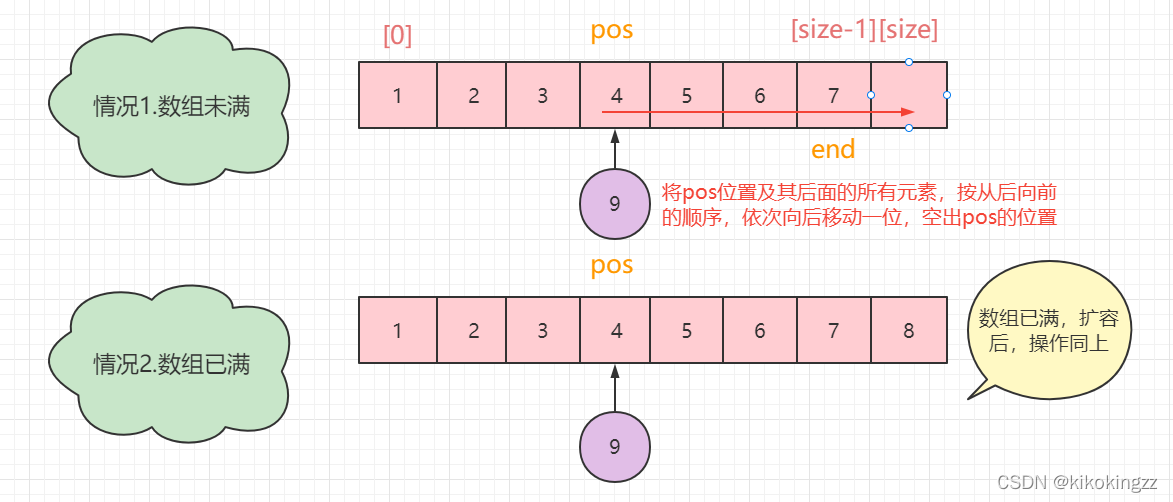
对于头插,我们发现依然会有两种情况:1.数组有剩余空间、2.数组已经满了,因此第一步仍然是进行判断数组空间是否已满,如果满了就执行扩容操作;然后按元素从后往前的顺序,依次将元素向后移动一位,将数组的第一个头空间空出来。
时间复杂度:O(N)
void SeqListPushFront(SeqList* sl, DataType x)//头插 { assert(sl);//声明sl,防止传入空指针 SeqListCheckCapacity(sl);//检测数组是否已满,满了就扩容 int end = sl->size - 1;//将end指向数组中最后一个元素 while (end >= 0)//从后往前挨个后移 { sl->a[end + 1] = sl->a[end];//end指向的元素后移 --end;//将end指向前一个元素 } sl->a[0] = x;//头插元素x sl->size++;//顺序表长度+1 }
(6)指定位置插入元素·SeqListInsert
该操作程序类似于头插,只不过这里与头插的区别在于,它的头不再是数组的第一个位置了,而是pos指向的位置[pos](可以说是一种头插的变式啦~)。
值得注意的是,在这里我们需要对pos的范围做一个规定,pos最前端可以达到数组的[0],此时相当于头插;pos最后端可以到达数组的 [size],此时相当于尾插。
时间复杂度:O(N)
void SeqListInsert(SeqList* sl, int pos, DataType x)//指定位置插入 { assert(sl);//声明sl,防止传入空指针 assert(pos >= 0&&pos<=sl->size);//规定pos允许插入的范围 SeqListCheckCapacity(sl); int end = sl->size - 1;//将end指向数组中最后一个元素 while (end >= pos)//将pos位置及后面元素从后往前挨个后移 { sl->a[end + 1] = sl->a[end];//将end指向的元素后移 --end;//将end指向前一个元素 } sl->a[pos] = x;//在pos位置插入元素x ++sl->size;//顺序表长度+1 }
升级版本:使用 size_t 定义pos
void SeqListInsert(SeqList* sl, size_t pos, DataType x)//改用无符号定义pos { assert(sl); assert(pos <= sl->size); SeqListCheckCapacity(sl); int end = sl->size - 1;//此处不可用size_t定义end while (end >= (int)pos)//这边进行大小比较时一定要进行强转 { sl->a[end + 1] = sl->a[end]; --end; } sl->a[pos] = x; ++sl->size; }此时我们需要注意,在while循环中进行end和pos的大小比较时,必须要将无符号的pos强制转换为int类型。
Q1:请问此处为什么不可用 size_t 定义end呢?
A1:因为当原数组没有元素时,即size为0时,这时end的值计算为-1,但由于size_t 定义的是无符号数,因此end的值会从有符号数的-1变化为无符号数的4294967295,进而导致后续程序出错。
Q2:为什么while循环中的判断语句要使用强转(int)呢?
A2:这是因为当原数组没有元素时,即size为0时,这时end的值计算为有符号数的-1,如果不对pos进行强转,有符号数与无符号数比较时,有符号数会整型提升为无符号数,此时有符号数的-1将会变为无符号数的最大数,此时必然大于pos,进而进入while循环。此时由于end 的值为-1,sl->a[end]会出现访问越界错误。
升级版本再改进
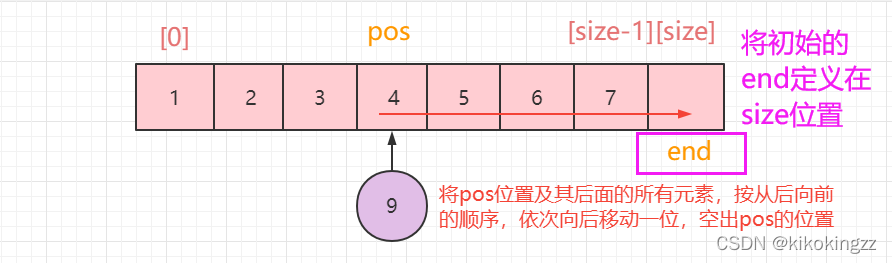
kiko:当然我们不难发现,这边主要的核心问题在于,end出现了负数情况,我们有没有办法让end始终保持非负状态呢?这样我们就无需进行强转操作了,答案是有的。
我们只需要将end更改指向为最后一个元素的后一个位置,这时就算原数组没有元素(size为0时),end的值也为0,是非负数,而pos的值最小为0,因此二者可以进行正常比较。
void SeqListInsert(SeqList* sl, size_t pos, DataType x)//改用无符号定义pos { assert(sl); assert(pos <= sl->size); SeqListCheckCapacity(sl); size_t end = sl->size ; while (end > pos) { sl->a[end] = sl->a[end-1]; --end; } sl->a[pos] = x; ++sl->size; }
(7)尾删元素·SeqListPopBack
在尾删元素过程中,我们一般只需要将顺序表中的size--即可,因为size的值代表的是顺序表中存储的有效元素长度,将其**--**,即将它的有效长度减1,相当于删除了最后一个元素;例如原本顺序表中有5个元素,这时使用size--后,该顺序表只有前4个元素有效,相当于尾删了一个元素。
时间复杂度:O(1)
PS:尾删时,我们不需要特意去清除最后一个元素的值,因为清除的物理本质是用一个值去替换原值,但我们无法确定新赋的值与原值是否相同,为了避免多此一举,因此直接**size--**,它不香吗?
void SeqListPopBack(SeqList* sl)//尾删 { assert(sl);//声明sl,防止传入空指针 if (sl->size > 0) { sl->size--;//顺序表的有效数据是依赖于size的 } }
(8)头删元素·SeqListPopFront
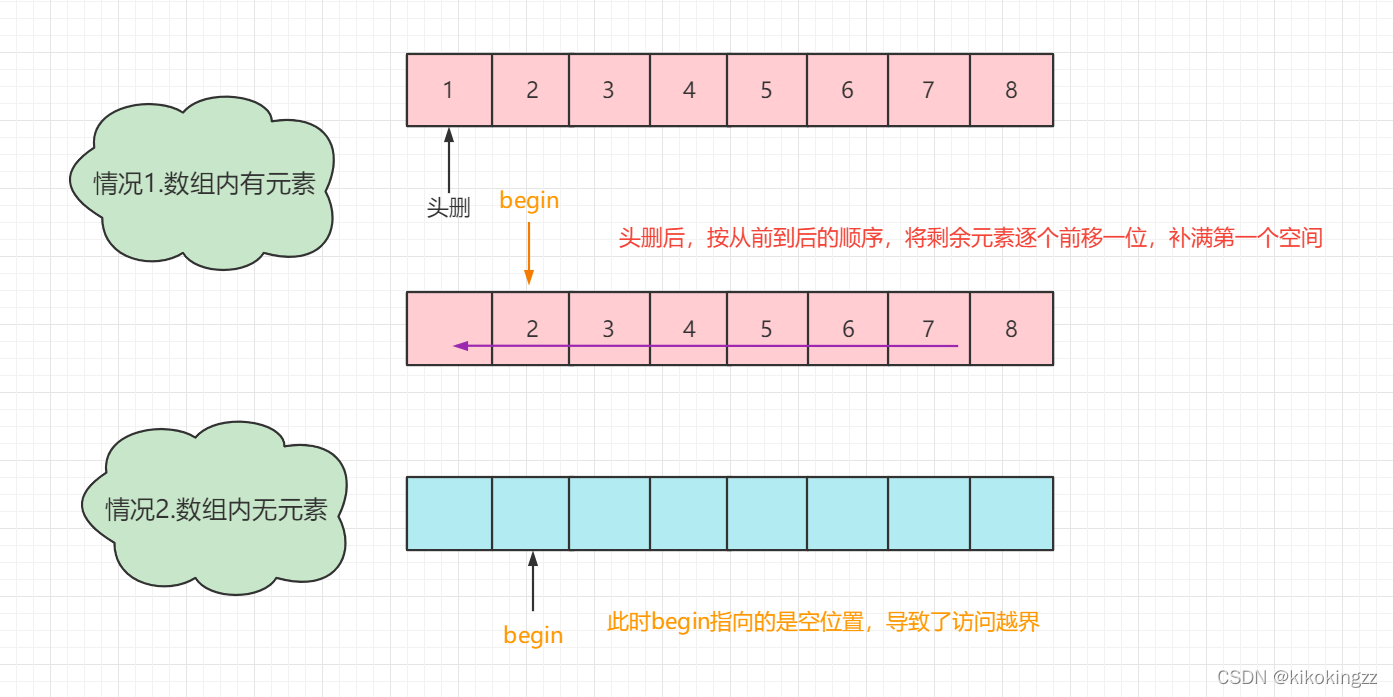
对于头删元素,我们需要与头插做对比。头删时我们需要将头部元素之后的所有元素,按从前到后的顺序,将这些元素逐个前移,这样第二个元素的值就会覆盖掉第一个元素的值,换句话说也就实现了头删的功能。
时间复杂度:O(N)
值得注意的是,begin选取的位置不同,最终设计出来的程序也会不同,我们此处将begin指向头部后一个元素。
void SeqListPopFront(SeqList* sl)//头删 { if (sl->size > 0)//当数组内有元素才可以头删 { int begin = 1; //当数组内只有一个元素时,直接跳过此步骤,直接-- while (begin < sl->size) { sl->a[begin - 1] = sl->a[begin]; ++begin; } --sl->size; } }
(9)指定位置删除元素·SeqListErase
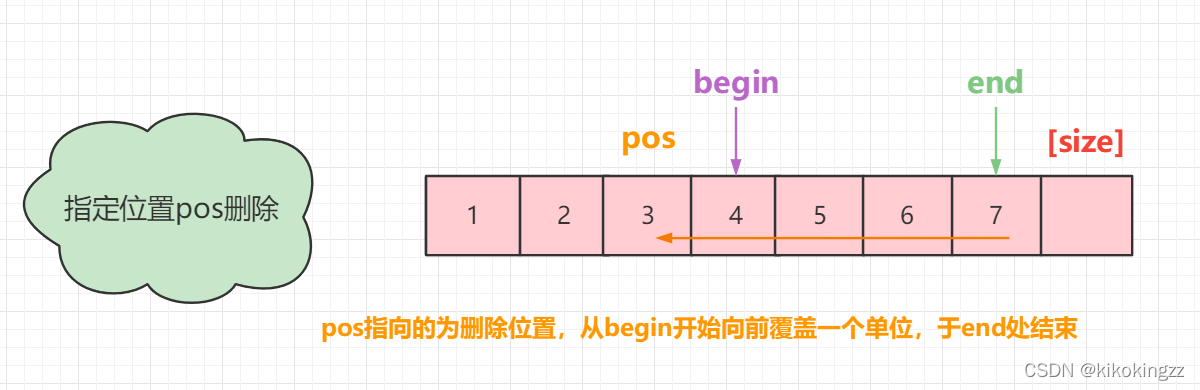
该操作程序类似于头删,只不过这里与头删的区别在于,它的头不再是数组的第一个位置了,而是pos指向的位置[pos](同样可以说是一种头删的变式啦~)。
因此,在这里我们也需要对pos的范围做一个规定,pos最前端可以达到数组的[0],此时相当于头删;pos最后端可以到达数组的 [size-1],此时相当于尾删,为了方便我们可以采用无符号 size_t 来定义pos。
void SeqListErase(SeqList* sl, size_t pos)//指定位置删除 { assert(sl); assert(pos < sl->size); size_t begin = pos + 1; while (begin < sl->size) { sl->a[begin - 1] = sl->a[begin]; ++begin; } sl->size--; }
(10)按值查找·SeqListFind
该操作通常与其他操作组合使用,例如在某个具体数值的前后插入元素、删除数组中所有值为特定数的元素等。
kiko:算是这么多操作里最简单的一个啦~
int SeqListFind(SeqList* sl, DataType x)//该函数的返回值为int型 { assert(sl); for (int i = 0; i < sl->size; ++i) { if (sl->a[i] == x) return i;//返回这个元素的数组下标 } return -1; }
✨✨✨我是分割线✨✨✨
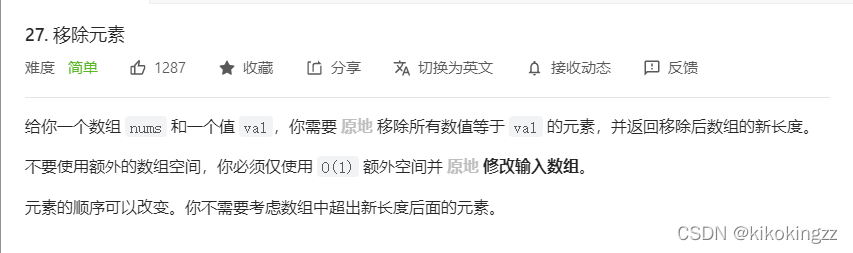
📝LeetCode之移除元素
思路1-依次挪动数据覆盖
思路:从前向后依次遍历找到数组中的元素,然后依次挪动后面的元素将其覆盖;重复此操作;用我们刚刚写的程序来描述就是,先使用SeqListFind找到对应元素,然后使用SeqListErase删除指定位置的元素,将此系列操作一直进行至遍历完整个数组。
优点:简单易想。
缺点:时间复杂度太大;最坏情况就是数组中所有元素都是需要删除的元素,此时时间复杂度达到了O(N^2)。
思路2-拷贝到新数组
思路:对原数组从前向后遍历,将不是val的值拷贝到新的数组中;最后再将新数组的元素拷贝回原数组,相当于对原数组进行了删除操作。
优点:时间复杂度为O(N)。
缺点:空间复杂度不符合要求,为O(N)。
思路3-拷贝到新数组(双指针)
思路:使用双指针,如果src指向的元素不为val,就将src指向的元素赋给dst,然后对src与dst同时++;当src指向的元素为val时,src++,dst不变;对上述2类操作一直重复至src遍历完整个数组,最终返回dst的值恰好就是有效数据的长度。
例如下例中dst,表示数组下标[2],而有数据为[0,3]的长度也为2,因此返回dst的值就好比返回了有效数组的长度,进而相当于删除了原数组的后续元素。
优点:时间复杂度为O(N)。
缺点:空间复杂度不符合要求,为O(N)。
代码实现:
int removeElement(int* nums, int numsSize, int val) { int src=0, dst=0; while(src<numsSize) { if(nums[src]!=val) { nums[dst]=nums[src]; src++; dst++; } else { src++; } } return dst; }

🌕写在最后
数据结构的世界是相当丰富的,内容方向繁多,但只要一步一个脚印,跟随【水滴计划】,水滴石穿,吃透、搞懂、拿捏住数据结构是完全没有问题的!后期该系列还会有视频教程和经验分享,关于更多这方面的内容,请关注本专栏哦!
热爱所热爱的, 学习伴随终生,kikokingzz与你同在!❥(^_-)
版权归原作者 kikokingzz 所有, 如有侵权,请联系我们删除。