一、拟合ARIMA模型
ARIMA是先运用差分运算得到平稳序列,再对平稳序列建立ARMA模型。差分运算可用diff****函数完成,命令格式为:
diff(x,lag=,differences=)
*其中:***x:**序列名
** lag:差分的步长(默认lag=1**)
** differences:差分次数(默认differences=1**)
常用命令有:
1阶差分:diff(x)
2阶差分:diff(x,1,2)
k阶差分:diff(x,1,k)
*d步差分:diff(x,d,1)或diff(x,d)*
1阶差分后再d步差分:diff(diff(x),d)
建立ARIMA模型采用arima函数,命令格式为:
** arima(x,order=c(p,d,q))**
疏系数模型,如果arima模型中有部分系数缺省,则称为疏系数模型,命令格式为:
** arima(x,order=,include.mean=,method=,transform.pars=,fixed=)**
其中:include.mean=T,需要拟合常数项
** include.mean=F,**不需要拟合常数项
** method:**指定参数估计的方法
** transform.pars=T,**不需要拟合疏系数模型
** transform.pars=F,**需要拟合疏系数模型
** fixed:**对疏系数模型指定疏系数的位置
- 对1917-1975美国23岁妇女每万人生育率序列建模
首先,读取数据,绘制时序图:
e<-read.table("E:/R/data/file18.csv",sep=",",header = T)
x<-ts(e$fertility,start = 1917)
plot(x)

从时序图可以看出序列非平稳,作1阶差分,并绘制1阶差分后的时序图:
x.dif<-diff(x)
plot(x.dif)
可以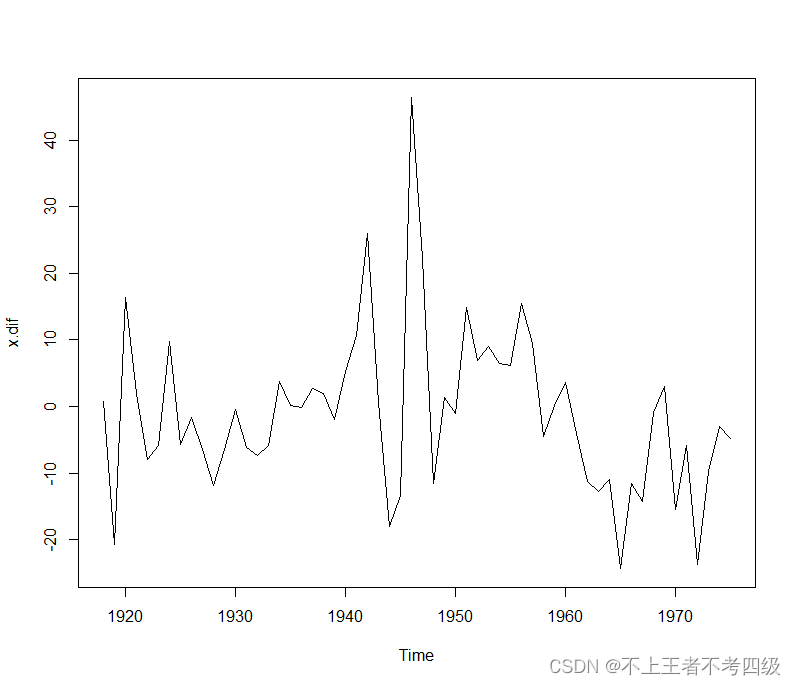
可以看出,1阶差分后时序图是平稳的,再绘制1阶差分后的自相关图和偏自相关图:
acf(x.dif)
pacf(x.dif)
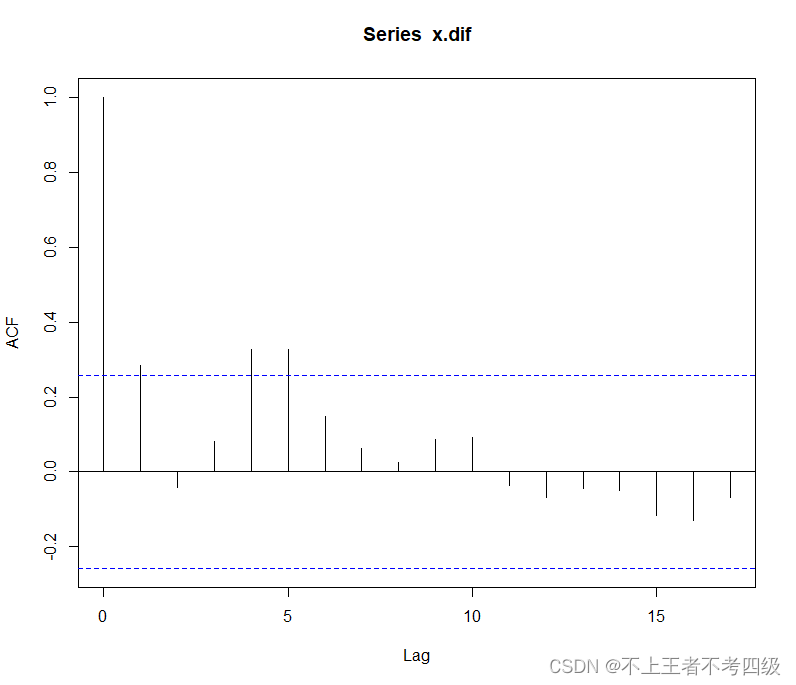
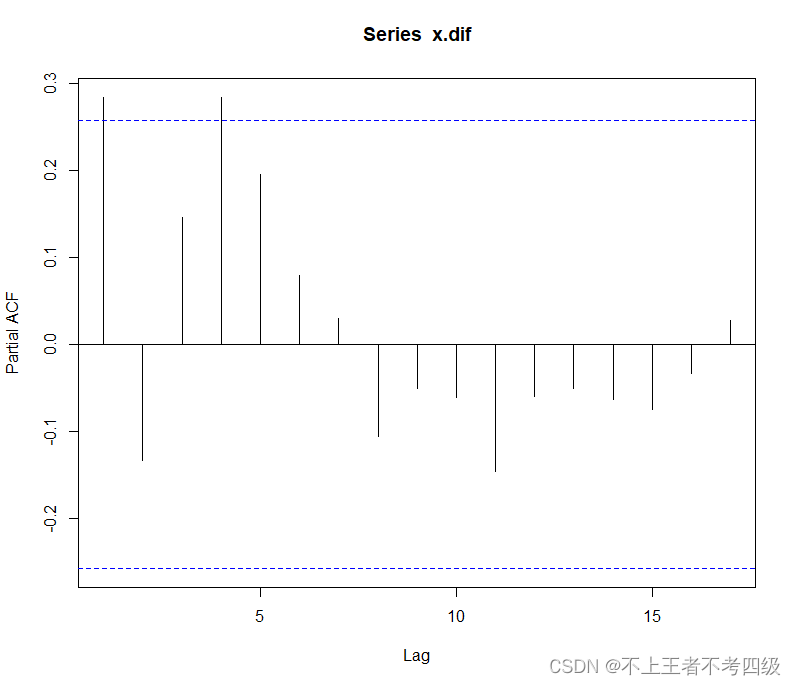
从偏自相关图看出,偏自相关系数4阶结尾,且延迟2阶和3阶的偏自相关系数很小,可以拟合疏系数模型****ARIMA((1,4),1,0)
输入:
x.fit<-arima(x,order = c(4,1,0),transform.pars = F,fixed = c(NA,0,0,NA))
x.fit
可以得出如下结果:

即模型为:

对残差作白噪声检验:
for(i in 1:2) print(Box.test(x.fit$residual,lag=6*i))

显示不能拒绝残差序列为白噪声序列。
二****季节模型
- 简单季节模型
简单季节模型是指趋势和季节效应的关系简单,可以通过趋势差分和季节差分得到平稳序列,并用ARMA模型拟合。可用arima函数中的seasonal选项拟合简单季节模型,命令格式为:
*arima(x,order=,include.mean=,method=,transform.pars=,fixed=,seasonal=)*
*其中:***include.mean=T,**需要拟合常数项
** include.mean=F,**不需要拟合常数项
** method:**指定参数估计的方法
** transform.pars=T,**不需要拟合疏系数模型
** transform.pars=F,**需要拟合疏系数模型
** fixed:**对疏系数模型指定疏系数的位置
** seasonl:**指定季节模型的阶数和季节周期,该选项格式为:
** seasonal=list(order=c(P,D,Q),period=)**
- 简单季节模型时,****P=0,Q=0
- 乘积季节模型时,P,Q至少有一个不为****0
*例*2 拟合1962-1991*年德国工人季节失业率序列*
首先,读取数据,并绘制时序图:
f<-read.table("E:/R/data/file19.csv",sep=",",header = T)
x<-ts(f$unemployment_rate,start = c(1962,1),frequency = 4)
plot(x)
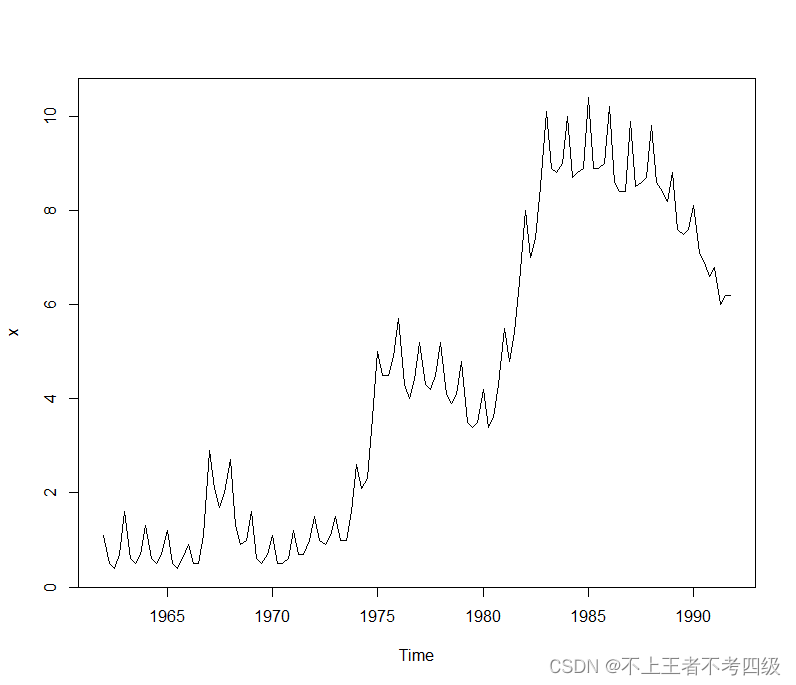
从时序图可以看出,序列非平稳,且有季节效应,周期为4。因此作1阶差分,再作4步差分,并绘制差分后时序图:
x.dif<-diff(diff(x),4)
plot(x.dif)
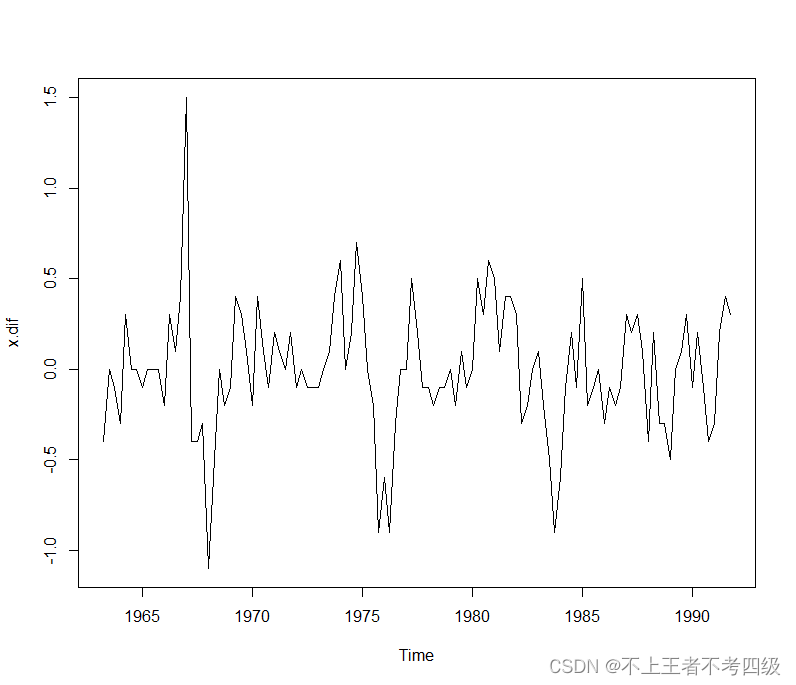
可以看出,差分后序列平稳,再绘制自相关图和偏自相关图:
acf(x.dif)
pacf(x.dif)
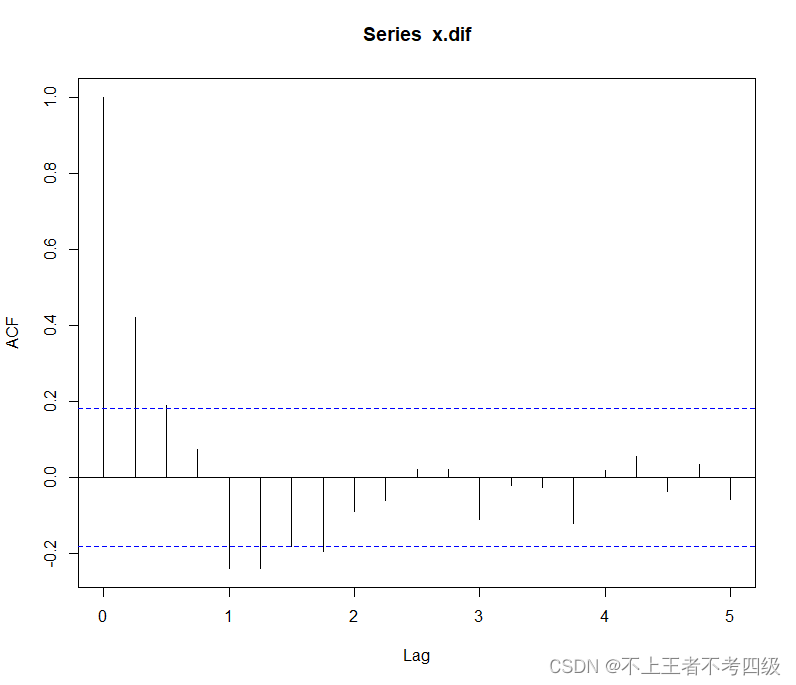
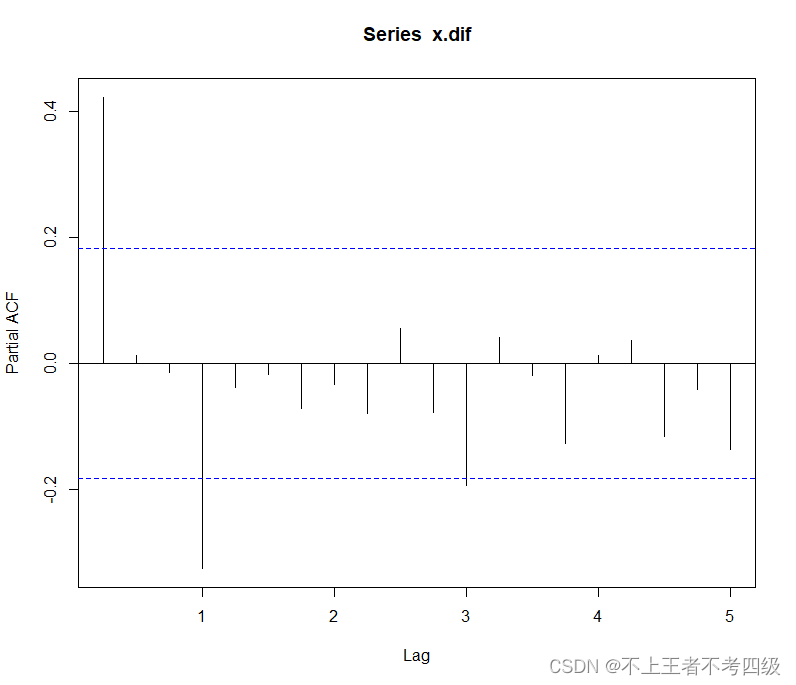
偏自相关系数4阶截尾,且延迟2阶3阶偏自相关系数很小,可以拟合疏系数的简单季节模型****ARIMA((1,4)(1,4),0)
输入命令:
x.fit<arima(x,order=c(4,1,0), transform.par=F,fixed = c(NA,0,0,NA),seasonal=list(order=c(0,1,0),period=4))
x.fit
可得如下结果:

即拟合模型为:
** **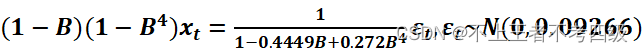
对参差序列作白噪声检验:
for(i in 1:2) print(Box.test(x.fit$residual,lag=6*i))
结果为:
** **
可见,参差序列为白噪声序列。
对序列作3年期预测,输入命令:
library(forecast)
x.fore<-forecast(x.fit,h=12)
x.fore
可得预测值:
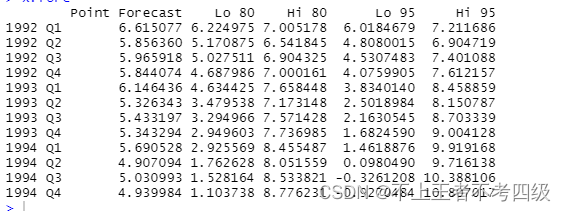
plot(x.fore)
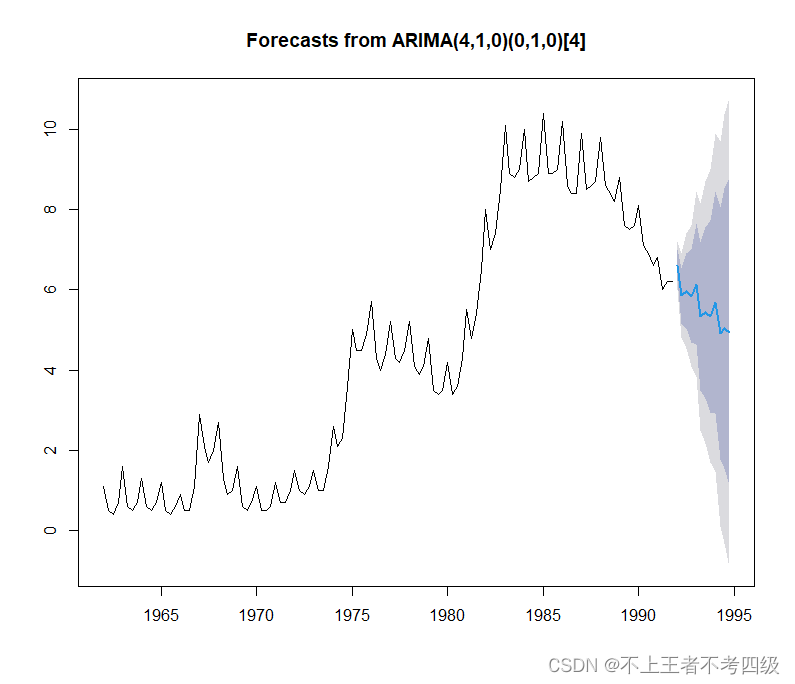
**2.**乘积季节模型
如果序列的趋势和季节效应关系复杂,简单差分不能完全提取出这些信息,则需要拟合乘积季节模型,一般形式为:

其中S为周期,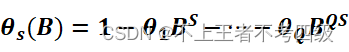
** **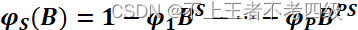
此模型简记为:** ARIMA(p,d,q)×(P,D,Q)S**
例3拟合1948-1981年美国女性月度失业率序列
首先,提取数据,绘制时序图:
g<-read.table("E:/R/data/file20.csv",sep=",",header = T)
x<-ts(g$unemployment_rate,start = c(1948,1),frequency = 12)
plot(x)
*从时序图上看出序列非平稳,且有周期性,周期为*12.因此,作1*阶差分,在做12步差分,观察差分后的时序图:*
x.dif<-diff(diff(x),12)
plot(x.dif)
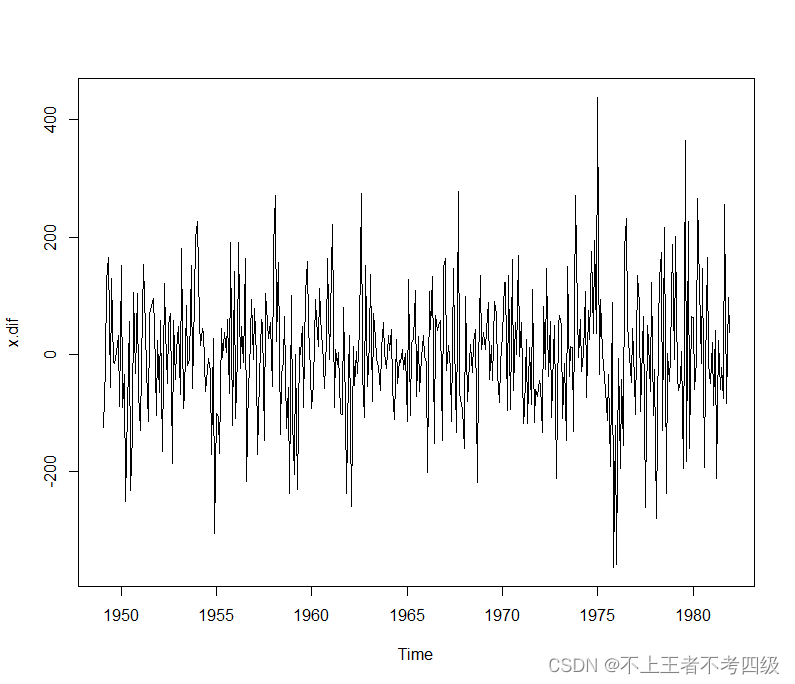
观察差分后的自相关图和偏自相关图:
acf(x.dif,lag=36)
pacf(x.dif,lag=36)
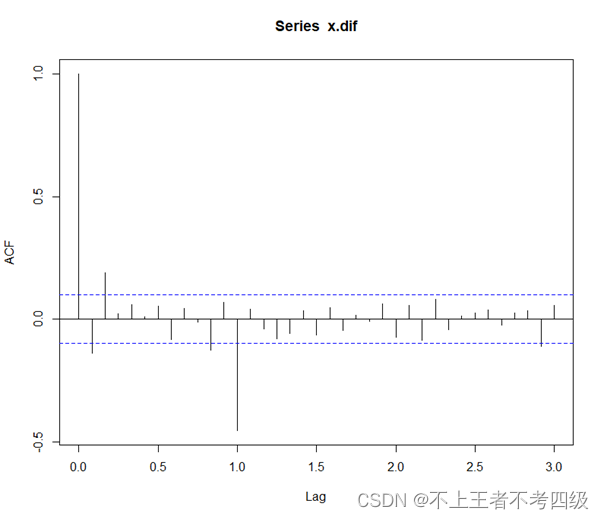
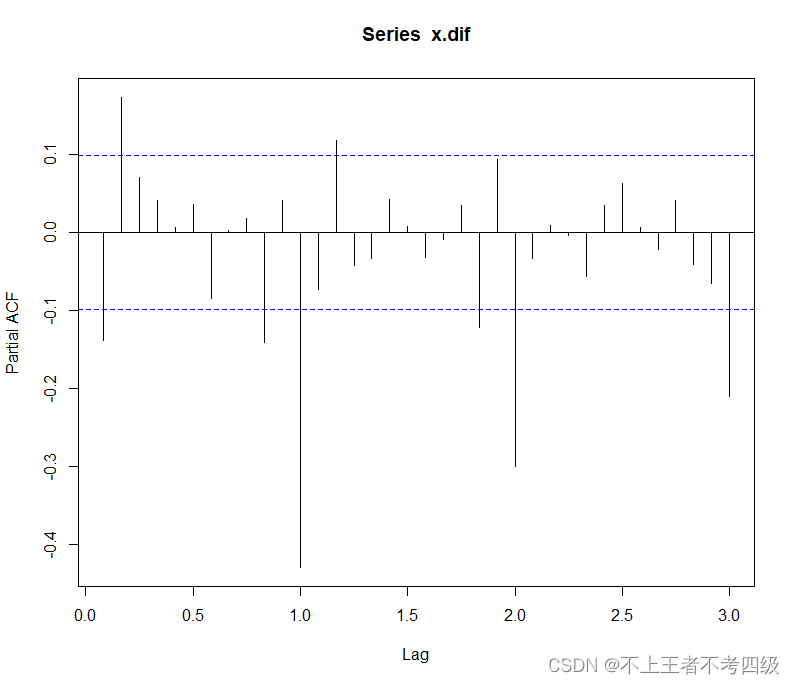
从自相关图上看,经过12步差分后的序列还有季节效应,且季节效应表现为自相关系数1个周期截尾,偏自相关系数拖尾,因此考虑乘积季节模型:*ARIMA(1,1,1)×******(0,1,1)*12,**即:
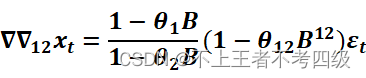
输入:
x.fit<-arima(x,order = c(1,1,1),seasonal = list(order=c(0,1,1),period=12))
x.fit
得出拟合结果:

即模型为:
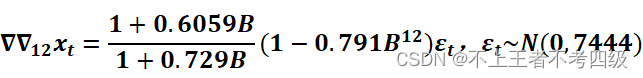
对残差作白噪声检验:
for(i in 1:2) print(Box.test(x.fit$residual,lag=6*i))
结果为:

P****值较大,不能拒绝原假设,即拟合模型显著
三残差自回归**(Auto-regressive)**模型
残差自回归模型的思想是先提取确定性因素(包括趋势和季节效应),再对残差拟合自回归模型。对趋势的提取有两种方法:
(1)自变量为时间t的幂函数:

(2)自变量为历史观察值:

*例*4 使用残差自回归模型拟合1952-1988*中国农业实际国民收入指数序列*
第1步:提取数据,拟合关于时间t的线性回归模型,记作模型(1):
d<-read.table("E:/R/data/file17.csv",sep=",",header = T)
x<-ts(d$index,start = 1952)
t<-c(1:37)
x.fit1<-lm(x~t)
summary(x.fit1)
结果为:
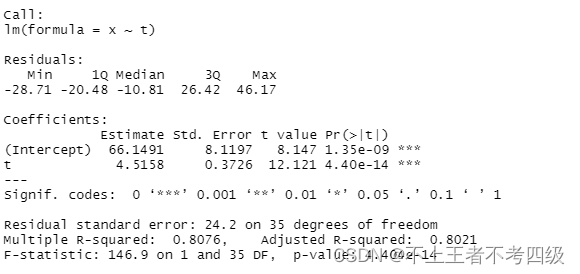
即:
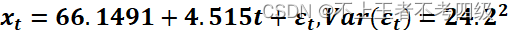
再拟合关于延迟变量的自回归模型,记为模型(2):
xlag<-x[2:37]
x2<-x[1:36]
x.fit2<-lm(x2~xlag)
summary(x.fit2)
结果为:
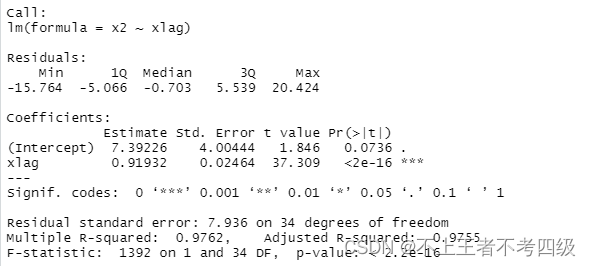
即:

两个模型拟合效果比较:
fit1<-ts(x.fit1$fitted.value,start = 1952)
fit2<-ts(x.fit2$fitted.value,start = 1952)
plot(x,type = "p",pch=8)
lines(fit1,col=2)
lines(fit2,col=4)
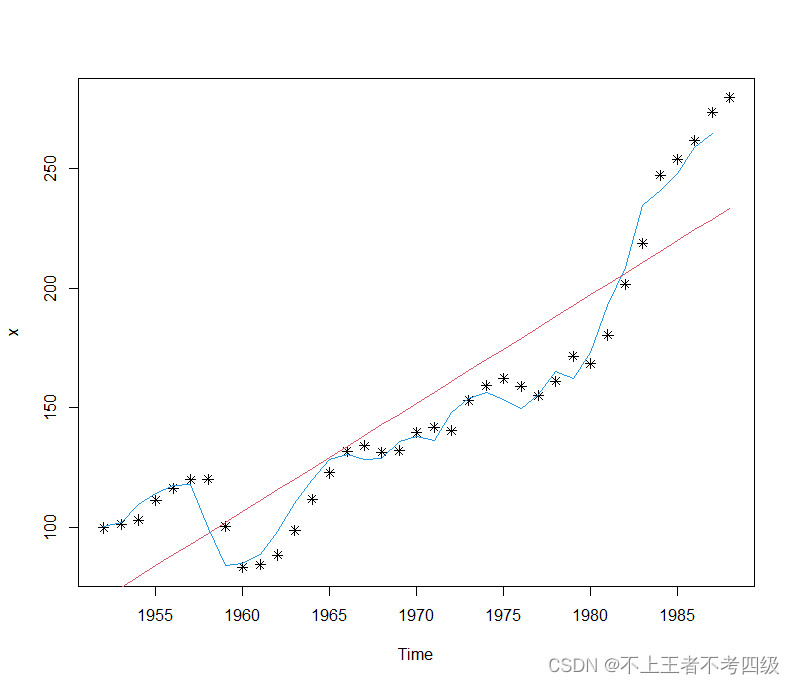
第2步:模型的残差自相关的检验,作DW检验之前,先要下载安装lmtest程序包,并加载,用其中的DW函数,对模型(1)的残差作检验,输入命令:
library(lmtest)
dwtest(x.fit1)
显示结果为:

可以看到,p值极小,要拒绝原假设,说明残差序列高度相关,因此,要对模型(1)的残差序列拟合自回归模型。
再对模型(2)的残差作Dh检验,输入命令:
dwtest(x.fit2,order.by=xlag)
得结果如下:

可以看出,p值较大,残差序列不存在相关性,因此不需要对模型(2)的残差拟合自回归模型。
第3步 对模型(1)的残差拟合自回归模型,首先观察残差的自相关图和偏自相关图:
acf(x.fit1$residual)
pacf(x.fit1$residual)
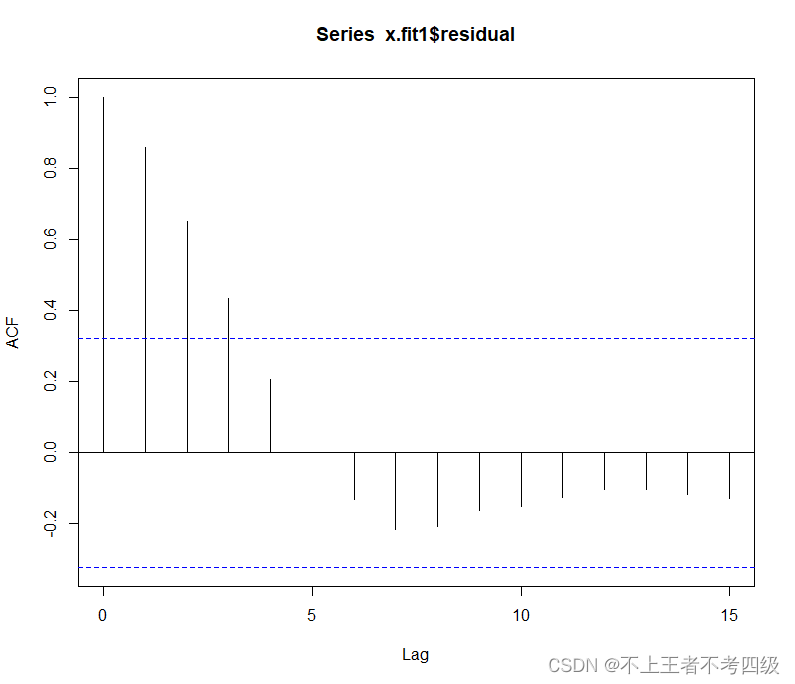
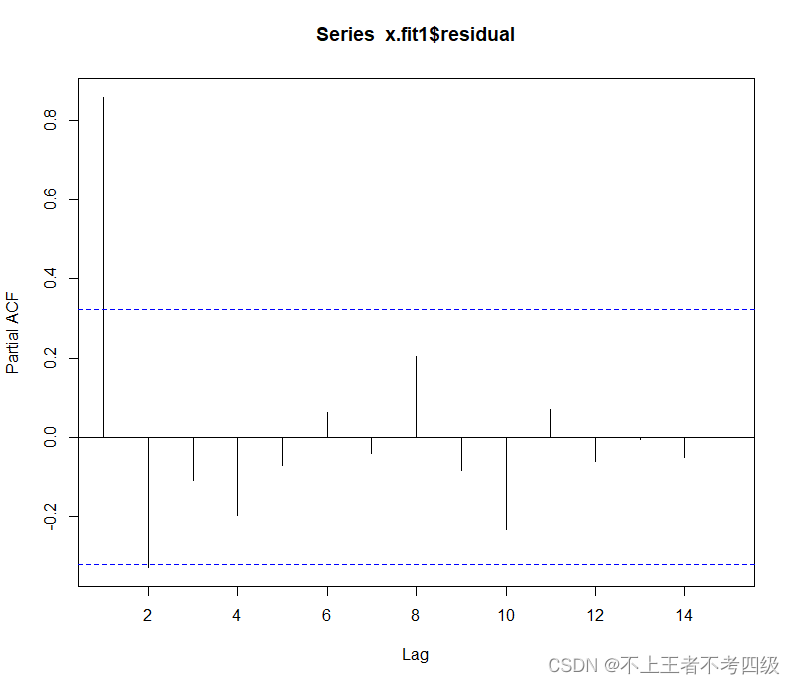
残差偏自相关系数2阶截尾,因此拟合AR(2)模型,输入:
r.fit<-arima(x.fit1$residual,order=c(2,0,0),include.mean = F)
r.fit
结果****为:

检验可知,新的残差序列为白噪声序列,因此,最后模型为:
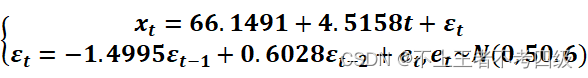
版权归原作者 qq_59382597 所有, 如有侵权,请联系我们删除。