学习时间:2022.04.09~2022.04.09
文章目录
2. BP神经网络
上一节了解了感知机模型(Perceptron),当结构上使用了多层的感知机递接连成一个前向型的网络时,就是一个多层感知机(MLP,Multilayer Perceptron),是一种前馈人工神经网络模型。
单个感知机只能实现二分类问题,MLP引入了隐含层(Hidden Layer),可用于多分类。
而BP神经网络,就是在MLP的基础上,引入非线性的激活函数,加入了BP(Back Propagation,反向传播)算法,采用了梯度下降等优化算法进行参数调优的神经网络。
简单理解:BP神经网络指的是用了“BP算法”进行训练的“多层感知机模型”。
2.1 理论基础
首先,从整体上理解一下BP神经网络的实现过程(实线代表正向传播,虚线代表反向传播)。
当完成了一次正反向传播,也就完成了一次神经网络的训练迭代,反复迭代,误差越来越小,完整的模型也就诞生了。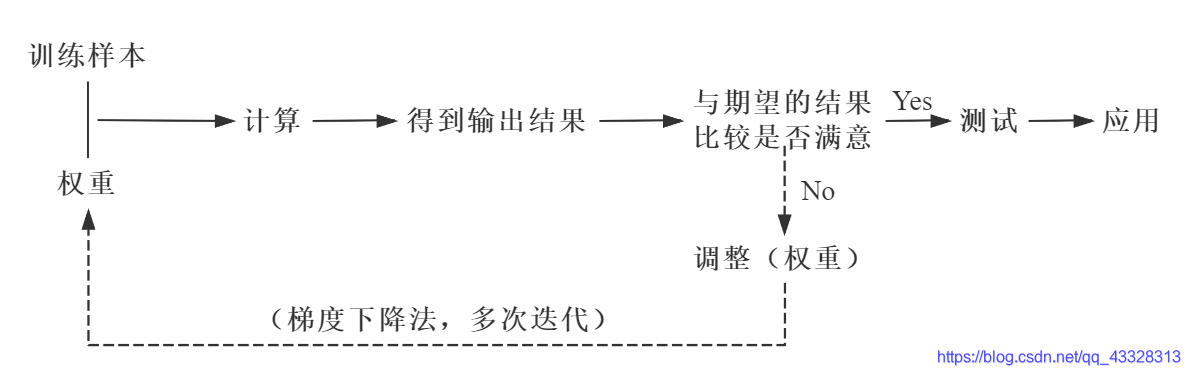
2.1.1 正向传播
数据(信息、信号)从输入端输入后,沿着网络的指向,乘以对应的权重后再加和,再将结果作为输入在激活函数中计算,将计算的结果作为输入传递给下一个节点。依次计算,直到得到最终结果。
通过每一层的感知器/神经元,层层计算,得到输出,每个节点的输出作为下一个节点的输入。这个过程就是正向传播。
2.1.2 反向传播
反向传播的基本思想就是通过计算输出层与期望值之间的误差来调整网络参数,从而使得误差变小,本质是一个“负反馈”的过程。
通过多次迭代,不断地对网络上的各个节点间的权重进行调整(更新),权重的调整(更新)采用梯度下降学习法。
反向传播的思想很简单,然而人们认识到它的重要作用却经过了很长的时间。后向传播算法产生于1970年,但它的重要性一直到David Rumelhart,Geoffrey Hinton和Ronald Williams于1986年合著的论文发表才被重视。
事实上,人工神经网络的强大力量几乎就是建立在反向传播算法基础之上的。反向传播基于四个基础等式,数学是优美的,仅仅四个等式就可以概括神经网络的反向传播过程,然而理解这种优美可能需要付出一些脑力。
2.1.3 梯度下降
在正向传播的过程中,有一个与期望的结果比较是否满意的环节,在这个环节中实际的输出结果与期望的输出结果之间就会产生一个误差,为了减小这个误差,这也就转换为了一个优化过程。
对于任何优化问题,总是会有一个目标函数 (objective function),这个目标函数就是损失函数(Loss Function)/代价函数(Cost Function)。让实际的输出结果与期望的输出结果之间的误差最小,就是利用梯度下降法原理,慢慢地寻找损失函数的最小值,从而得到模型的最终参数。
梯度下降法 是一个很重要很重要的计算方法,要说明这个方法的原理,就又涉及到另外一个问题:逻辑回归。下面只用一个图进行一个简单地说明。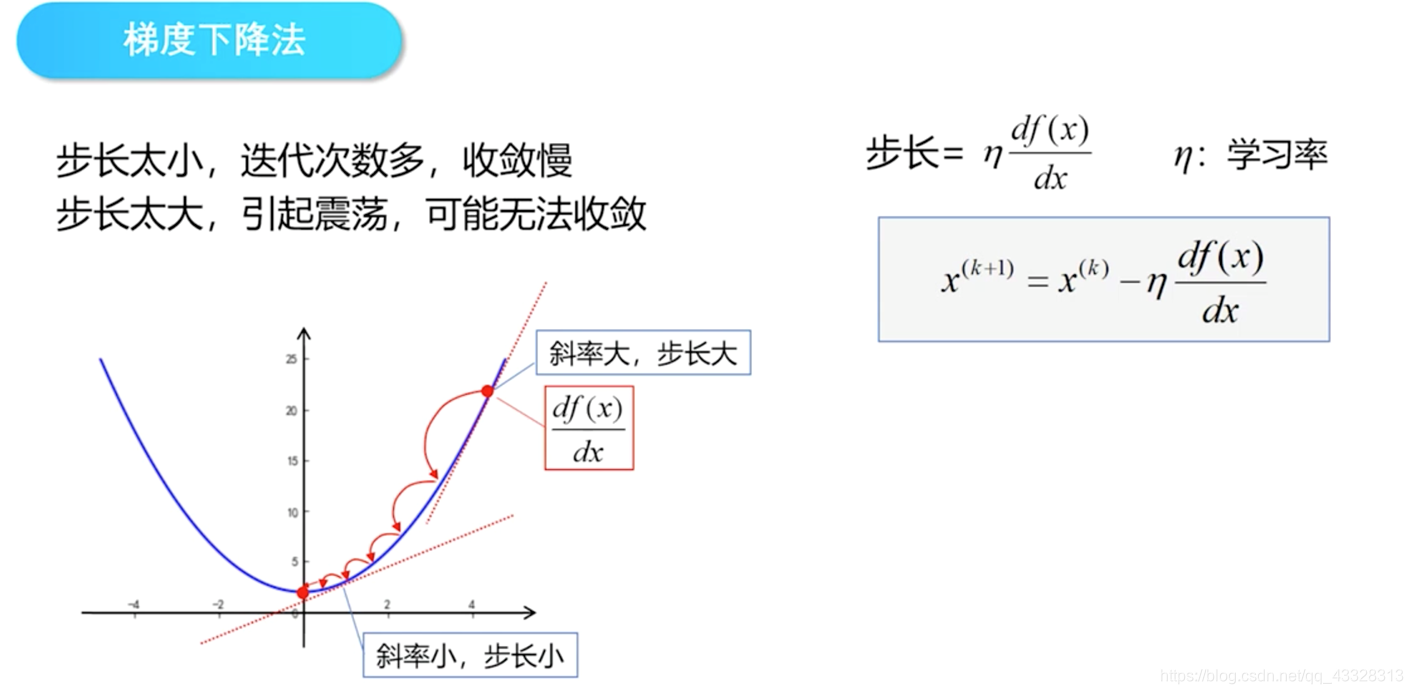
假设上图中的曲线就是损失函数的图像,它存在一个最小值。梯度是一个利用求导得到的数值,可以理解为参数的变化量。从几何意义上来看,梯度代表一个损失函数增加最快的方向,反之,沿着相反的方向就可以不断地使损失逼近最小值,也就是使网络逼近真实的关系。
那么反向传播的过程就可以理解为,根据损失loss ,来反向计算出每个参数(如
u
1
,
1
,
u
1
,
2
u_{1,1}, u_{1,2}
u1,1,u1,2等的梯度
d
(
u
1
,
1
)
,
d
(
u
1
,
2
)
,
…
d(u_{1,1}), d(u_{1,2}), …
d(u1,1),d(u1,2),…等等,再将原来的参数分别加上自己对应的梯度,就完成了一次反向传播。
但实际中的梯度下降学习法,有些像高山滑雪运动员总是在寻找坡度最大的地段向下滑行。当他处于A点位置时,沿最大坡度路线下降,达到局部极小点,则停止滑行;如果他是从B点开始向下滑行,则他最终将达到全局最小点。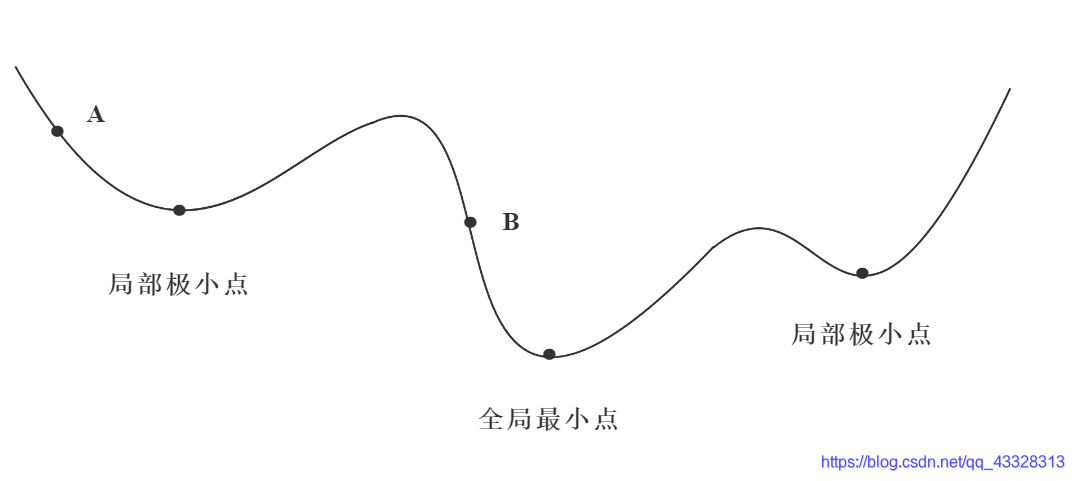
补充:逻辑回归
逻辑函数:Sigmoid函数。
可以看出逻辑函数的导函数可以转化成本身的一个表达式,这在后面用梯度下降法求解参数时会用到。
g ( y ) = e y 1 + e y 经 转 换 : g ′ ( y ) = g ( y ) ⋅ [ 1 − g ( y ) ] g(y) = \frac{e^y}{1+e^y}\\经转换:g'(y) = g(y)·[1 - g(y)] g(y)=1+eyey经转换:g′(y)=g(y)⋅[1−g(y)]
逻辑回归的原理:用逻辑函数把线性回归的结果
( − ∞ , + ∞ ) (-∞,+∞) (−∞,+∞)映射到 ( 0 , 1 ) (0,1) (0,1)。(把线性回归函数的结果y,放到sigmod函数中去,就构造了**逻辑回归函数**。)用公式描述上面这句话:
g ( y ) = 1 1 + e − y = 1 1 + e − ( θ 0 + θ 1 x 1 + … + θ n x n ) = 1 1 + e − θ γ x g(y) = \frac{1}{1+e^{-y}} = \frac{1}{1+e^{-(θ_0+θ_1x_1+…+θ_nx_n)}} = \frac{1}{1+e^{-θ^γx}} g(y)=1+e−y1=1+e−(θ0+θ1x1+…+θnxn)1=1+e−θγx1转换一下逻辑回归函数,过程如下:
g ( y ) = 1 1 + e − y → y = l n g ( y ) 1 − g ( y ) g(y) = \frac{1}{1+e^{-y}} → y = ln^{\frac{g(y)}{1-g(y)}} g(y)=1+e−y1→y=ln1−g(y)g(y)
2.2 BP算法原理
来源:一文搞定BP神经网络。
2.2.1 四个等式
首先,使用以下符号约定:
W j k l W_{jk}^l Wjkl表示:从网络中第 ( l − 1 ) (l-1) (l−1)层中的第 k k k个神经元指向第 l l l层中的第 j j j个神经元的连接的权重;b j l b_j^l bjl表示:第 l l l层中第 j j j个神经元的偏置;z j l z_j^l zjl表示:第 l l l层中第 j j j个神经元的线性结果(权值求和);a j l a_j^l ajl表示:第 l l l层中第 j j j个神经元的激活函数输出的值;σ σ σ表示:激活函数。因此,第 l l l层中第 j j j个神经元的激活值为: a j l = σ ( ∑ k W j k l ⋅ a k l − 1 + b j l ) a_j^l = σ(\sum_k W_{jk}^l·a_k^{l-1} + b_j^l) ajl=σ(∑kWjkl⋅akl−1+bjl)
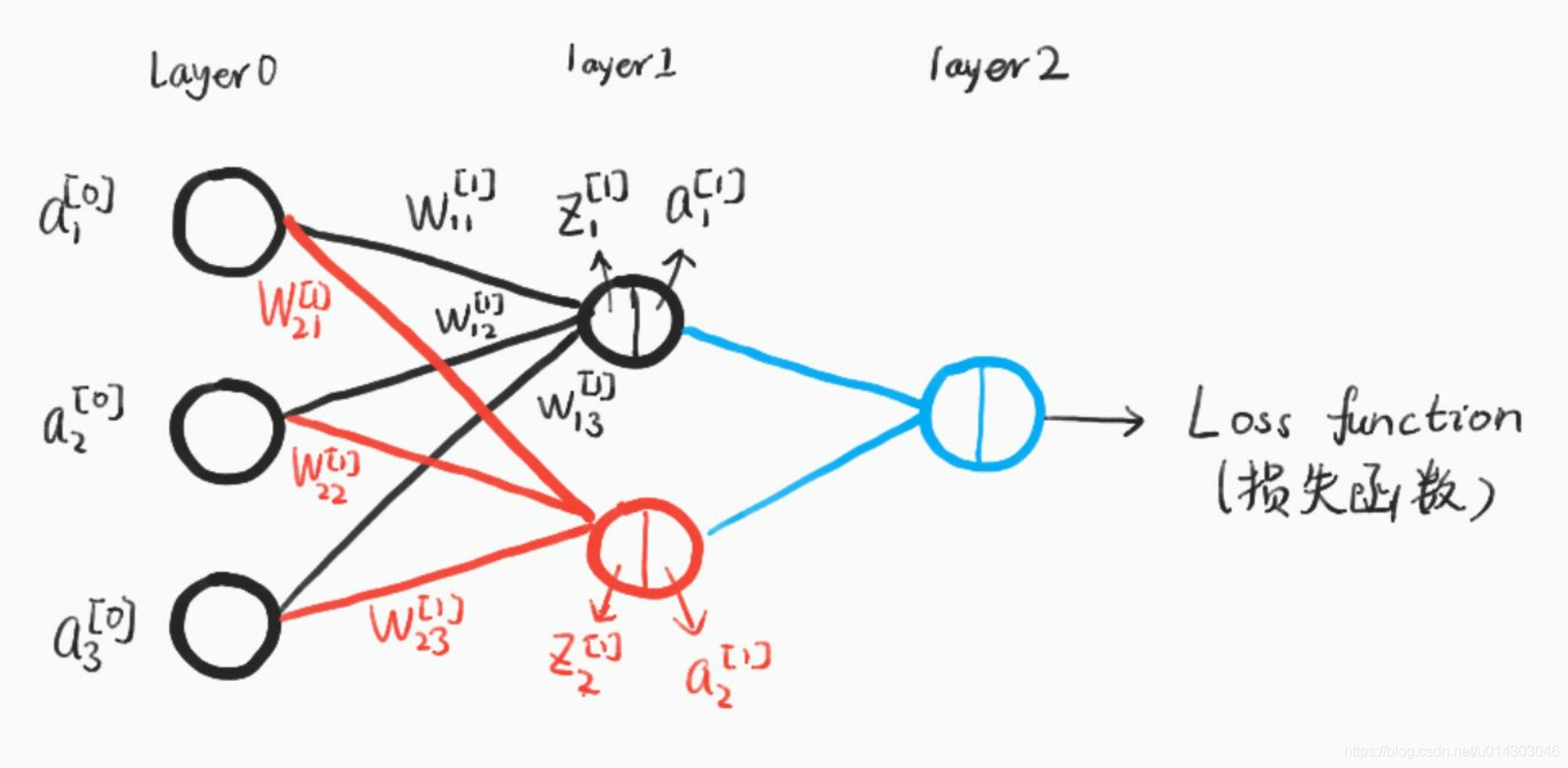
反向传播能够知道如何更改网络中的权重W WW和偏置
b bb来改变代价函数值。最终这意味着它能够计算偏导数
∂ L ( a l , y ) ∂ W j k l \frac{∂L(a^l,y)}{∂W_{jk}^l}∂Wjkl∂L(al,y)和
∂ L ( a l , y ) ∂ b j l \frac{∂L(a^l,y)}{∂b_j^l}∂bjl∂L(al,y)。为了计算这些偏导数,我们首先引入一个中间变量
δ j l δ_j^lδjl,代表:网络中第
l ll层中第
j jj个神经元的误差,由反向传播计算得出。如果为第
l ll层第
j jj个神经元添加一个扰动
Δ z j l Δz_j^lΔzjl,使得损失函数或者代价函数变小,那么就是一个好的扰动。
Δ z j l Δz_j^lΔzjl与
δ j l = ∂ L ( a l , y ) ∂ z j l δ_j^l = \frac{∂L(a^l,y)}{∂z_j^l}δjl=∂zjl∂L(al,y)符号相反。于是,每一层的误差向量可以表示为:
δ j l = [ δ 1 l δ 2 l … δ 2 n ] δ_j^l = \begin{bmatrix}δ_1^l\\δ_2^l\\…\\δ_2^n\end{bmatrix}δjl=⎣⎢⎢⎡δ1lδ2l…δ2n⎦⎥⎥⎤。下面开始介绍反向传播原理的四个基础等式。
输出层误差( L L L表示输出层层数):
δ j L = ∂ L ∂ a j L ⋅ σ ′ ( z j L ) δ_j^L = \frac{∂L}{∂a_j^L}·σ'(z_j^L)δjL=∂ajL∂L⋅σ′(zjL)
隐含层误差:
δ j L = ∑ k W k j l + 1 ⋅ δ k l + 1 ⋅ σ ′ ( z j L ) δ_j^L = \sum_k W_{kj}^{l+1}·δ_k^{l+1}·σ'(z_j^L)δjL=k∑Wkjl+1⋅δkl+1⋅σ′(zjL)
参数变化率:
∂ L ∂ b j l = δ j l ∂ L ∂ W j k l = a k l − 1 ⋅ δ j l \frac{∂L}{∂b_j^l} = δ_j^l\\ \frac{∂L}{∂W_{jk}^l} = a_k^{l-1}·δ_j^l∂bjl∂L=δjl∂Wjkl∂L=akl−1⋅δjl
参数更新规则( α α α为学习率):
b j l ← b j l − α ∂ L ∂ b j l W j k l ← W j k l − α ∂ L ∂ W j k l b_j^l ← b_j^l - α\frac{∂L}{∂b_j^l}\\ W_{jk}^l ← W_{jk}^l - α\frac{∂L}{∂W_{jk}^l}bjl←bjl−α∂bjl∂LWjkl←Wjkl−α∂Wjkl∂L
总结如下:

- 超参数:
神经网络模型中有一些参数是需要设计者给出的,也有一些参数是模型自己求解的。
比如,学习率
α
α
α,隐含层的层数,每个隐含层的神经元个数,激活函数的选取,损失函数(代价函数)的选取等等,这些需要模型设计者确定的参数被称之为**超参数**。
其它的参数,比如权重矩阵
W
W
W和偏置系数
b
b
b在确定了超参数之后是可以通过模型的计算来得到的,这些参数称之为普通参数,简称**参数**。
2.2.2 推导和计算
建立一个典型的三层神经网络结构,如下图: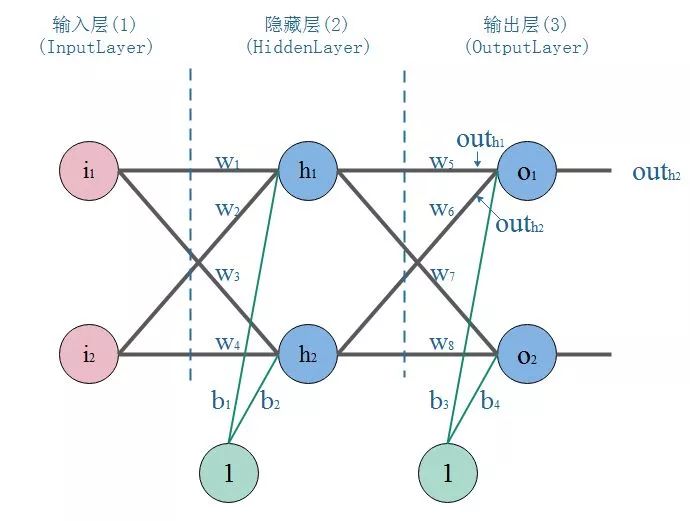
- 参数初始化:
输入:特征
i
1
=
0.1
i_1 = 0.1
i1=0.1,
i
2
=
0.2
i_2 = 0.2
i2=0.2;
输出:预期结果
O
1
=
0.01
O_1 = 0.01
O1=0.01,
O
2
=
0.99
O_2 = 0.99
O2=0.99;
初始权重:
W
1
=
0.1
,
W
2
=
0.2
,
W
3
=
0.3
,
W
4
=
0.4
W
5
=
0.5
,
W
6
=
0.6
,
W
7
=
0.7
,
W
8
=
0.8
W_1 = 0.1, W_2 = 0.2, W_3 = 0.3, W_4 = 0.4\\W_5 = 0.5, W_6 = 0.6, W_7 = 0.7, W_8 = 0.8
W1=0.1,W2=0.2,W3=0.3,W4=0.4W5=0.5,W6=0.6,W7=0.7,W8=0.8;
偏置:
b
1
=
0.55
,
b
2
=
0.56
,
b
3
=
0.66
,
b
4
=
0.67
b_1 = 0.55, b_2 = 0.56, b_3 = 0.66, b_4 = 0.67
b1=0.55,b2=0.56,b3=0.66,b4=0.67。
- 正向传播(输入层→隐含层):
计算隐含层神经元
h
1
h_1
h1的输入加权和:
i
n
h
1
=
W
1
⋅
i
1
+
W
2
⋅
i
2
+
1
⋅
b
1
=
0.1
×
0.1
+
0.2
×
0.2
+
1
×
0.55
=
0.6
in_{h_1} = W_1·i_1 + W_2·i_2 + 1·b_1 = 0.1×0.1+0.2×0.2+1×0.55 = 0.6
inh1=W1⋅i1+W2⋅i2+1⋅b1=0.1×0.1+0.2×0.2+1×0.55=0.6;
通过激活函数Sigmoid计算隐含层神经元
h
1
h_1
h1的输出:
o
u
t
h
1
=
1
e
i
n
h
1
+
1
=
1
e
−
0.6
+
1
=
0.6456563062
out_{h_1} = \frac{1}{e^{in_{h_1}}+1} = \frac{1}{e^{-0.6}+1} = 0.6456563062
outh1=einh1+11=e−0.6+11=0.6456563062;
同理计算出隐含层神经元
h
2
h_2
h2的输出:
o
u
t
h
2
=
0.6592603884
out_{h_2} = 0.6592603884
outh2=0.6592603884。
- 正向传播(隐含层→输出层):
计算输出层神经元
O
1
O_1
O1的输入加权和:
i
n
O
1
=
W
5
⋅
o
u
t
h
1
+
W
6
⋅
o
u
t
h
2
+
1
⋅
b
3
=
0.5
×
0.6456563062
+
0.6
×
0.6592603884
+
1
×
0.66
=
1.3783843861
in_{O_1} = W_5·out_{h_1} + W_6·out_{h_2} + 1·b_3 = 0.5×0.6456563062+0.6×0.6592603884+1×0.66 = 1.3783843861
inO1=W5⋅outh1+W6⋅outh2+1⋅b3=0.5×0.6456563062+0.6×0.6592603884+1×0.66=1.3783843861;
计算输出层神经元
O
1
O_1
O1的输出:
o
u
t
O
1
=
1
e
i
n
O
1
+
1
=
1
e
−
1.3789843861
+
1
=
0.7987314002
out_{O_1} = \frac{1}{e^{in_{O_1}}+1} = \frac{1}{e^{-1.3789843861}+1} = 0.7987314002
outO1=einO1+11=e−1.3789843861+11=0.7987314002;
同理计算出隐含层神经元
O
2
O_2
O2的输出:
o
u
t
O
2
=
0.8374488853
out_{O_2} = 0.8374488853
outO2=0.8374488853。
- 对比输出结果:
输出层的输出结果:
[
0.7987314002
,
0.8374488853
]
[0.7987314002, 0.8374488853]
[0.7987314002,0.8374488853],期望结果
[
0.01
,
0.99
]
[0.01, 0.99]
[0.01,0.99],明显的差太远了,这个时候我们就需要利用反向传播,更新权值
W
W
W,然后重新计算输出。
- 反向传播(计算输出误差):
此处使用均方误差(MSE)作为损失函数:
E
t
o
t
a
l
=
∑
i
=
1
2
E
o
u
t
O
1
=
1
2
(
O
1
−
o
u
t
O
1
)
2
+
1
2
(
O
2
−
o
u
t
O
2
)
2
=
0.0116359213
+
0.3110486109
=
0.3226845322
E_{total} = \sum^2_{i=1} E_{out_{O_1}} = \frac{1}{2}(O_1 - out_{O_1})^2 + \frac{1}{2}(O_2 - out_{O_2})^2 = 0.0116359213+0.3110486109 = 0.3226845322
Etotal=∑i=12EoutO1=21(O1−outO1)2+21(O2−outO2)2=0.0116359213+0.3110486109=0.3226845322;
PS:使用均方误差(MSE)作为例子,是因为计算比较简单,实际上用的时候效果不怎么样。
如果激活函数是饱和的,带来的缺陷就是系统迭代更新变慢,系统收敛就慢,当然这是可以有办法弥补的,一种方法是使用交叉熵函数作为损失函数。
交叉熵做为代价函数能达到上面说的优化系统收敛下欧工,是因为它在计算误差对输入的梯度时,抵消掉了激活函数的导数项,从而避免了因为激活函数的“饱和性”给系统带来的负面影响。
- 反向传播(更新隐含层→输出层的权值 W W W,以 W 5 W_5 W5为例):
我们知道,权重
W
W
W的大小能直接影响输出,
W
W
W不合适会使得输出存在误差。要想直到某一个
W
W
W值对误差影响的程度,可以用误差对该
W
W
W的变化率来表达。如果
W
W
W的一点点变动,就会导致误差增大很多,说明这个w对误差影响的程度就更大,也就是说,误差对该
W
W
W的变化率越高。而误差对
W
W
W的变化率就是误差对
W
W
W的**偏导**。
因此,根据链式法则有:
∂
E
t
o
t
a
l
∂
W
5
=
∂
E
t
o
t
a
l
∂
o
u
t
O
1
⋅
∂
o
u
t
O
1
∂
i
n
O
1
⋅
∂
i
n
O
1
∂
W
5
\frac{∂E_{total}}{∂W_5} = \frac{∂E_{total}}{∂out_{O_1}}·\frac{∂out_{O_1}}{∂in_{O_1}}·\frac{∂in_{O_1}}{∂W_5}
∂W5∂Etotal=∂outO1∂Etotal⋅∂inO1∂outO1⋅∂W5∂inO1。
按顺序计算:
∂
E
t
o
t
a
l
∂
o
u
t
O
1
=
0.7887314002
\frac{∂E_{total}}{∂out_{O_1}} = 0.7887314002
∂outO1∂Etotal=0.7887314002,
∂
o
u
t
O
1
∂
i
n
O
1
=
0.1607595505
\frac{∂out_{O_1}}{∂in_{O_1}} = 0.1607595505
∂inO1∂outO1=0.1607595505,
∂
i
n
O
1
∂
W
5
=
0.6456563062
\frac{∂in_{O_1}}{∂W_5} = 0.6456563062
∂W5∂inO1=0.6456563062;
联立:
∂
E
t
o
t
a
l
∂
W
5
=
∂
E
t
o
t
a
l
∂
o
u
t
O
1
⋅
∂
o
u
t
O
1
∂
i
n
O
1
⋅
∂
i
n
O
1
∂
W
5
=
0.7887314002
×
0.1607595505
×
0.6456563062
=
0.0818667051
\frac{∂E_{total}}{∂W_5} = \frac{∂E_{total}}{∂out_{O_1}}·\frac{∂out_{O_1}}{∂in_{O_1}}·\frac{∂in_{O_1}}{∂W_5} = 0.7887314002×0.1607595505×0.6456563062 = 0.0818667051
∂W5∂Etotal=∂outO1∂Etotal⋅∂inO1∂outO1⋅∂W5∂inO1=0.7887314002×0.1607595505×0.6456563062=0.0818667051;
因此,更新的
W
5
W_5
W5的值为:
W
5
′
=
W
5
−
α
⋅
∂
E
t
o
t
a
l
∂
W
5
=
0.5
−
0.5
×
0.0818667051
=
0.45906664745
W'_5 = W_5 - α·\frac{∂E_{total}}{∂W_5} = 0.5-0.5×0.0818667051 = 0.45906664745
W5′=W5−α⋅∂W5∂Etotal=0.5−0.5×0.0818667051=0.45906664745,同理可以计算出
W
6
′
,
W
7
′
,
W
8
′
W'_6,W'_7,W'_8
W6′,W7′,W8′的值。
- 反向传播(更新隐含层→输出层的偏置 b b b,以 b 3 b_3 b3为例):
同理,更新偏置,有:
∂
E
t
o
t
a
l
∂
b
3
=
∂
E
t
o
t
a
l
∂
o
u
t
O
1
⋅
∂
o
u
t
O
1
∂
i
n
O
1
⋅
∂
i
n
O
1
∂
b
3
\frac{∂E_{total}}{∂b_3} = \frac{∂E_{total}}{∂out_{O_1}}·\frac{∂out_{O_1}}{∂in_{O_1}}·\frac{∂in_{O_1}}{∂b_3}
∂b3∂Etotal=∂outO1∂Etotal⋅∂inO1∂outO1⋅∂b3∂inO1,且:
∂
i
n
O
1
∂
b
3
=
1
\frac{∂in_{O_1}}{∂b_3} = 1
∂b3∂inO1=1。
联立:
∂
E
t
o
t
a
l
∂
b
3
=
∂
E
t
o
t
a
l
∂
o
u
t
O
1
⋅
∂
o
u
t
O
1
∂
i
n
O
1
⋅
∂
i
n
O
1
∂
b
3
=
0.7887314002
×
0.1607595505
×
1
=
0.12679610536
\frac{∂E_{total}}{∂b_3} = \frac{∂E_{total}}{∂out_{O_1}}·\frac{∂out_{O_1}}{∂in_{O_1}}·\frac{∂in_{O_1}}{∂b_3} = 0.7887314002×0.1607595505×1 = 0.12679610536
∂b3∂Etotal=∂outO1∂Etotal⋅∂inO1∂outO1⋅∂b3∂inO1=0.7887314002×0.1607595505×1=0.12679610536;
因此,更新的
b
3
b_3
b3的值为:
b
3
′
=
b
3
−
α
⋅
∂
E
t
o
t
a
l
∂
b
3
=
0.66
−
0.5
×
0.12679610536
=
0.59660194732
b'_3 = b_3 - α·\frac{∂E_{total}}{∂b_3} = 0.66-0.5×0.12679610536 = 0.59660194732
b3′=b3−α⋅∂b3∂Etotal=0.66−0.5×0.12679610536=0.59660194732,,同理可以计算出
b
4
′
b'_4
b4′的更新值。
- 反向传播(更新输入层→隐含层的权值 W W W和偏置,以 W 1 W_1 W1为例):
仔细观察,我们在求
W
5
W_5
W5的更新,误差反向传递路径输出层→隐层,即out(O1)→in(O1)→w5,总误差只有一根线能传回来。但是求
W
1
W_1
W1时,误差反向传递路径是隐藏层→输入层,但是隐藏层的神经元是有**2根线**的,所以总误差沿着2个路径回来,也就是说,计算偏导时,要分开来算。
即:
∂
E
t
o
t
a
l
∂
W
1
=
∂
E
t
o
t
a
l
∂
o
u
t
h
1
⋅
∂
o
u
t
h
1
∂
i
n
i
n
1
⋅
∂
i
n
i
n
1
∂
W
1
=
(
∂
E
O
1
∂
o
u
t
h
1
+
∂
E
O
2
∂
o
u
t
h
1
)
⋅
∂
o
u
t
h
1
∂
i
n
i
n
1
⋅
∂
i
n
i
n
1
∂
W
1
=
(
∂
E
O
1
∂
i
n
O
1
⋅
∂
i
n
O
1
∂
o
u
t
h
1
+
∂
E
O
1
∂
i
n
O
1
⋅
∂
i
n
O
1
∂
o
u
t
h
2
)
⋅
∂
o
u
t
h
1
∂
i
n
i
n
1
⋅
∂
i
n
i
n
1
∂
W
1
\frac{∂E_{total}}{∂W_1} = \frac{∂E_{total}}{∂out_{h_1}}·\frac{∂out_{h_1}}{∂in_{in_1}}·\frac{∂in_{in_1}}{∂W_1} \\= (\frac{∂E_{O_1}}{∂out_{h_1}} + \frac{∂E_{O_2}}{∂out_{h_1}})·\frac{∂out_{h_1}}{∂in_{in_1}}·\frac{∂in_{in_1}}{∂W_1} \\= (\frac{∂E_{O_1}}{∂in_{O_1}}·\frac{∂in_{O_1}}{∂out_{h_1}} + \frac{∂E_{O_1}}{∂in_{O_1}}·\frac{∂in_{O_1}}{∂out_{h_2}})·\frac{∂out_{h_1}}{∂in_{in_1}}·\frac{∂in_{in_1}}{∂W_1}
∂W1∂Etotal=∂outh1∂Etotal⋅∂inin1∂outh1⋅∂W1∂inin1=(∂outh1∂EO1+∂outh1∂EO2)⋅∂inin1∂outh1⋅∂W1∂inin1=(∂inO1∂EO1⋅∂outh1∂inO1+∂inO1∂EO1⋅∂outh2∂inO1)⋅∂inin1∂outh1⋅∂W1∂inin1,结果为:
∂
E
t
o
t
a
l
∂
W
1
=
0.0011362635
\frac{∂E_{total}}{∂W_1} = 0.0011362635
∂W1∂Etotal=0.0011362635。
因此,更新的
W
1
W_1
W1的值为:
W
1
′
=
W
1
−
α
⋅
∂
E
t
o
t
a
l
∂
W
1
=
0.1
−
0.1
×
0.0011362635
=
0.0998863737
W'_1 = W_1 - α·\frac{∂E_{total}}{∂W_1} = 0.1-0.1×0.0011362635 = 0.0998863737
W1′=W1−α⋅∂W1∂Etotal=0.1−0.1×0.0011362635=0.0998863737,同理可以计算出
W
2
′
,
W
3
′
,
W
4
′
W'_2,W'_3,W'_4
W2′,W3′,W4′的值,以及,同理可以计算出偏置
b
1
′
,
b
2
′
b'_1, b'_2
b1′,b2′的值。
偏置和权重可以采用不同的学习率,每一层之间也可以采用不同的学习率。
到此,计算出所有更新的权重和偏置,完成了1次迭代训练,可以重新进行第二次正向传播。随着迭代的次数加深,输出层的误差会越来越小,模型趋于收敛。
版权归原作者 新四石路打卤面 所有, 如有侵权,请联系我们删除。
