前言
时间序列的目的:进行预测,**根据已有的时间序列数据预测未来**。思路是确定已有的时间序列变化模式,并假定这种模式会延续到未来。不考虑事物发展之间的因果。
时间序列可简化为两部分:趋势和季节性,以及两者之外的随机变动。
1 时间序列定义
** 时间序列**是事物在不同时间上的相继观察值排列而成的序列。时间序列中的时间可以是可以是年份、季度、月份或其他任何时间形式。
** 本文所用的数据文件**:链接:https://pan.baidu.com/s/1mZhZDNX4Vzt4tONi7xCcnw?pwd=52ts
提取码:52ts
1.1 朴素法
朴素法就是预测值等于实际观察到的最后一个值。它假设数据是平稳且没有趋势性与季节性的。通俗来说就是以后的预测值都等于最后的值。
这种方法很明显适用情况极少,所以我们重点通过这个方法来熟悉一下数据可视化与模型的评价及其相关代码。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")#不显示警告信息
df = pd.read_csv('time_series_data.csv')
df.info()
# 按照天聚合数据
df.Timestamp = pd.to_datetime(df.Datetime,format='%d-%m-%Y %H:%M')
df.index = df.Timestamp
df_ts = df.resample('D').sum()
df_ts
#2012 年 8 月- 2013 年 10 月用作训练数据,2013 年 11 月 – 2013 年 12 月用作测试数据。
train = df_ts['2012-08-25':'2013-10-31']
test = df_ts['2013-11-1':'2013-12-31']
train.tail()
#朴素法
dd = np.asarray(train['Count'])#训练组数据
y_hat = test.copy()#测试组数据
y_hat['naive'] = dd[len(dd) - 1]#预测组数据
#数据可视化
plt.figure(figsize=(12, 8))
plt.plot(train.index, train['Count'], label='Train')
plt.plot(test.index, test['Count'], label='Test')
plt.plot(y_hat.index, y_hat['naive'], label='Naive Forecast')
plt.legend(loc='best')
plt.title("Naive Forecast")
plt.show()
得到预测结果为:

我们可以通过计算**均方根误差**检验模型**准确率**。其中**均方根误差(RMSE)**是各数据偏离真实值的距离平方和的平均数的开方。
#计算均方根误差RMSE
from sklearn.metrics import mean_squared_error
from math import sqrt
# mean_squared_error求均方误差
rmse = sqrt(mean_squared_error(test['Count'], y_hat['naive']))
print(rmse)
得到RMSE=1053,可见朴素法的误差非常大。
1.2 简单平均法
预测值等于之前过去所有值的平均。这种方法也不准确,但在某些情况下非常有效。
#简单平均法
y_hat_avg = test.copy()#测试组数据
y_hat_avg['avg_forecast'] = train['Count'].mean()#预测组数据
plt.figure(figsize=(12,8))
plt.plot(train['Count'], label='Train')
plt.plot(test['Count'], label='Test')
plt.plot(y_hat_avg['avg_forecast'], label='Average Forecast')
plt.legend(loc='best')
plt.show()
预测结果为:

得到RMSE=2637.
1.3 移动平均法
有一种数据集,价格在某些时间大幅上升或下降。此时我们用简单平均法,就得使用所有先前数据的平均值,但这是不合理的,因为开始的数据会大幅影响预测情况。因此,我们可以**只取近段时期的数据。**
这种用某些窗口期计算平均值的预测方法就叫**移动平均法**。
#移动平均法
y_hat_avg = test.copy()#测试数据
#利用时间窗函数rolling求平均值u
y_hat_avg['moving_avg_forecast'] = train['Count'].rolling(60).mean().iloc[-1]#预测数据
plt.figure(figsize=(16,8))
plt.plot(train['Count'], label='Train')
plt.plot(test['Count'], label='Test')
plt.plot(y_hat_avg['moving_avg_forecast'], label='Moving Average Forecast')
plt.legend(loc='best')
plt.show()
得到预测结果为:

RMSE为1121
1.4 指数平滑法
在做时序预测时,一个显然的思路是:**认为离着预测点越近的点,作用越大**。假设随着时间的变化,权重以指数方式下降,年代久远的数据权重将接近于0。
将权重按照指数级进行衰减,这就是指数平滑法的基本思想。
指数平滑法有几种不同形式:一次指数平滑法针对**没有趋势和季节性**的序列,二次指数平滑法针对**有趋势但没有季节性**的序列,三次指数平滑法针对**有趋势也有季节性**的序列。“
所有的指数平滑法都要更新上一时间步长的计算结果,并使用当前时间步长的数据中包含的新信息。它们通过”混合“新信息和旧信息来实现,而相关的新旧信息的权重由一个可调整的参数来控制。
我们可以通过**调整平滑系数**,决定把多大比例的“随机”变动当成规律性的变动——平滑系数越大,我们认为随机变动中的规律性比例就越高。
1.4.1 一次指数平滑
一次指数平滑法的递推关系如下:

其中s为时间步长i(第i个时间点)上经过平滑后的值,x则为时间步长i上的实际数据。a的区间是0到1,它控制着新旧信息之间的平衡:当a接近1,只保留当前数据点;当a接近0,只保留前面的平滑值(整个曲线都是平的)。
递推关系式:

在指数平滑法中,所有先前的观测值都对当前的平滑值产生了影响,但它们所起的作用随着参数 α 幂的增大而逐渐减小。那些相对较早的观测值所起的作用相对较小。同时,称α为记忆衰减因子可能更合适——因为α的值越大,模型对历史数据“遗忘”的就越快。从某种程度来说,指数平滑法就像是拥有无限记忆(平滑窗口足够大)且权值呈指数级递减的移动平均法。一次指数平滑所得的计算结果可以在数据集及范围之外进行扩展,因此也就可以用来进行预测。
预测方式为:

s为最后一个算出来的值。h等于1代表预测的第一个值。
python代码:
#一次指数平滑
from statsmodels.tsa.api import SimpleExpSmoothing
y_hat_avg = test.copy()
fit = SimpleExpSmoothing(np.asarray(train['Count'])).fit(smoothing_level=0.6, optimized=False)
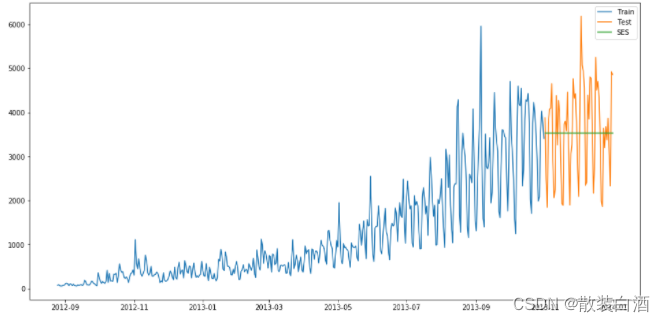
y_hat_avg['SES'] = fit.forecast(len(test))
plt.figure(figsize=(16, 8))
plt.plot(train['Count'], label='Train')
plt.plot(test['Count'], label='Test')
plt.plot(y_hat_avg['SES'], label='SES')
plt.legend(loc='best')
plt.show()
结果为RMSE=1040
1.4.2 二次指数平滑
二次指数平滑在一次指数平滑的基础上,将趋势作为一个额外考量,保留了趋势的详细信息。我们要保留并更新两个量:平滑后的数据和平滑后的趋势。
公式如下:

当前趋势告诉我们在上一个时间步长里平滑信号改变了多少。要想使趋势平滑,我们用一次指数平滑法对趋势进行处理,并使用参数 β 。临近的趋势权重大。
若要利用该计算结果进行预测,就取最后那个平滑值,然后每增加一个时间步长就在该平滑值上增加一次最后那个平滑趋势:

python代码:
from statsmodels.tsa.api import Holt
y_hat_avg = test.copy()
fit = Holt(np.asarray(train['Count'])).fit(smoothing_level=0.3, smoothing_slope=0.1)
y_hat_avg['Holt_linear'] = fit.forecast(len(test))
结果为RMSE=1033
1.4.3 三次指数平滑
如果数据集在一定时间段内的固定区间内呈现相似的模式,那么该数据集就具有季节性。二次指数平滑考虑了序列的基数和趋势,三次指数平滑在此基础上添加了一个季节分量。
公式如下:
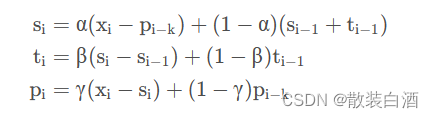
P_i是指“周期性部分”,k为周期的长度,预测公式如下:

在使用二次平滑模型与三次平滑模型前,我们可以使用sm.tsa.seasonal_decompose分解时间序列,可以得到以下分解图形——从上到下依次是原始数据、趋势数据、周期性数据、随机变量(残差值)。根据分析图形和数据可以确定对应的季节参数。
python代码:
#三次指数平滑
from statsmodels.tsa.api import ExponentialSmoothing
y_hat_avg = test.copy()
fit1 = ExponentialSmoothing(np.asarray(train['Count']), seasonal_periods=7, trend='add', seasonal='add', ).fit()
y_hat_avg['Holt_Winter'] = fit1.forecast(len(test))
结果RMSE=575,我们可以看到趋势和季节性的预测准确度很高。我们可以通过调整参数优化模型。
1.5 AR模型
AR(Auto Regressive Model)自回归模型是线性时间序列分析模型中最简单的模型。通过自身前面部分的数据与后面部分的数据之间的相关关系(自相关)来建立回归方程,从而可以进行预测或者分析。服从p阶的自回归方程表达式如下:
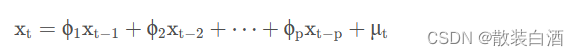
其中μ表示白噪声,是时间序列中的数值的随机波动,但是这些波动会相互抵消,最终是0。**p为自回归系数**。
所以当只有一个时间记录点时,称为一阶自回归过程,即AR(1)。其表达式为:

利用Python建立AR模型一般会用到我们之后会说到的ARIMA模型(AR模型中的p是ARIMA模型中的参数之一,只要将其他的参数设置为0即为AR模型)。您可以先阅读后续ARIMA模型的内容并参考文件中的代码查看具体的内容。
1.6 MA模型
MA(Moving Average Model)移动平均模型通过将一段时间序列中白噪声(误差)进行加权和,可以得到移动平均方程。如下模型为q阶移动平均过程,表示为MA(q),**q是移动平均阶数**。

**当前时间点的值由前q期的误差来决定**,μ为常数项,相当于普通回归中的截距项;**μ_t为当前时间点的随机误差**。MA模型的核心思想是每一期的随机误差都会影响当期值,把前q期的所有误差加起来就是对t期值的影响。
同样,利用Python建立MA模型一般会用到我们之后会说到的ARIMA模型,您可以先阅读后续ARIMA模型的内容并参考文件中的代码查看具体的内容。
1.7 ARMA模型
ARMA(Auto Regressive and Moving Average Model)自回归移动平均模型是与自回归和移动平均模型两部分组成。所以可以表示为ARMA(p, q)。**p是自回归阶数,q是移动平均阶数**。

从式子中就可以看出,自回归模型结合了两个模型的特点,其中,AR可以解决当前数据与后期数据之间的关系,MA则可以解决随机变动也就是噪声的问题。
1.8 ARIMA模型
**ARIMA(Auto Regressive Integrate Moving Average Model)差分自回归移动平均模型**是在ARMA模型的基础上进行改造的,ARMA模型是针对t期值进行建模的,而ARIMA是针对t**期与t-d期之间差值**进行建模,我们把这种不同期之间做差称为**差分**,这里的**d是几就是几阶差分**。ARIMA模型也是基于平稳的时间序列的或者差分化后是稳定的,另外前面的几种模型都可以看作ARIMA的某种特殊形式。表示为**ARIMA(p, d, q)**。**p为自回归阶数,q为移动平均阶数,d为时间成为平稳时所做的差分次数**,也就是Integrate单词的在这里的意思。
具体步骤如下:
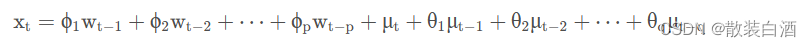
我们可以看到ARIMA模型的形式基本与ARMA的形式是一致的,只不过把x换成了w。
** python代码:**
from statsmodels.tsa.arima_model import ARIMA
ts_ARIMA= train['Count'].astype(float)
fit1 = ARIMA(ts_ARIMA, order=(7, 1, 4)).fit()
y_hat_ARIMA = fit1.predict(start="2013-11-1", end="2013-12-31", dynamic=True)
plt.figure(figsize=(16, 8))
plt.plot(train['Count'], label='Train')
plt.plot(test['Count'], label='Test')
plt.plot(y_hat_ARIMA, label='ARIMA')
plt.legend(loc='best')
plt.show()
最终RMSE为3723.
1.9 SARIMA模型
SARIMA季节性自回归移动平均模型模型在ARIMA模型的基础上添加了季节性的影响,结构参数有七个:SARIMA(p,d,q)(P,D,Q,s)
其中p,d,q分别为之前ARIMA模型中我们所说的p:趋势的自回归阶数。d:趋势差分阶数。q:趋势的移动平均阶数。
P:季节性自回归阶数。
D:季节性差分阶数。
Q:季节性移动平均阶数。
s:单个季节性周期的时间步长数。
import statsmodels.api as sm
y_hat_avg = test.copy()
fit1 = sm.tsa.statespace.SARIMAX(train.Count, order=(2, 1, 4), seasonal_order=(0, 1, 1, 7)).fit()
y_hat_avg['SARIMA'] = fit1.predict(start="2013-11-1", end="2013-12-31", dynamic=True)
plt.figure(figsize=(16, 8))
plt.plot(train['Count'], label='Train')
plt.plot(test['Count'], label='Test')
plt.plot(y_hat_avg['SARIMA'], label='SARIMA')
plt.legend(loc='best')
plt.show()
结果RMSE=933
2 时间序列预测模型优缺点
**适用范围**: 根据客观事物发展的这种连续规律性, 运用过去的历史数据, 通过统计分析, 进一步推测市场未来的发展趋势。 时间序列, 在时间序列分析预测法处于核心位置。
**优点**: 一般用 ARMA 模型拟合时间序列, 预测该时间序列未来值。 Daniel 检验平稳性。 自动回归 AR(Auto regressive) 和 移动平均 MA(Moving Average)预测模型。
**缺点**: 当遇到外界发生较大变化, 往往会有较大偏差, 时间序列预测法对于中短期预测的效果要比长期预测的效果好。
在后续的文章中我们将讲解如何确定数据的平稳性与数据预处理,为后续时间序列的建模做准备.
参考文章:https://blog.csdn.net/qq_42692386/article/details/108619863
版权归原作者 汽水啤酒花 所有, 如有侵权,请联系我们删除。