
线性回归是最流行和讨论最多的模型之一,它无疑是深入机器学习(ML)的入门之路。这种简单、直接的建模方法值得学习,这是进入ML的第一步。

在继续讨论之前,让我们回顾一下线性回归可以大致分为两类。
简单线性回归:当只有一个输入变量时,它是线性回归最简单的形式。
多元线性回归:这是一种线性回归的形式,当有两个或多个预测因子时使用。
我们将看到多个输入变量如何共同影响输出变量,同时还将了解计算与简单LR模型的不同之处。我们还将使用Python构建一个回归模型。
最后,我们将深入学习线性回归,学习共线性、假设检验、特征选择等内容。
现在有人可能会想,我们也可以用简单的线性回归来分别研究我们对所有自变量的输出。
为什么需要线性回归
从多个输入变量预测结果。但是,真的是这样吗?
考虑到这一点,假设你要估算你想买的房子的价格。你知道建筑面积,房子的年代,离你工作地点的距离,这个地方的犯罪率等等。
现在,这些因素中的一些将会对房价产生积极的影响。例如,面积越大,价格越高。另一方面,工作场所的距离和犯罪率等因素会对你对房子的估计产生负面影响。
简单线性回归的缺点:当我们只对一个结果感兴趣时,运行单独的简单线性回归会导致不同的结果。除此之外,可能还有一个输入变量本身与其他一些预测器相关或依赖于其他一些预测器。这可能会导致错误的预测和不满意的结果。
这就是多元线性回归发挥作用的地方。
数学公式
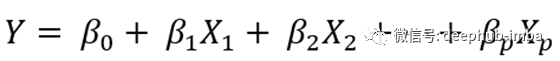
这里,Y是输出变量,X项是相应的输入变量。注意,这个方程只是简单线性回归的延伸,和每个指标都有相应的斜率系数(β)。
β的第一个参数(βo)是拦截常数和Y的值是在缺乏预测(我。e当所有X项都为0时),它在给定的回归问题中可能有意义,也可能有意义,也可能没有意义。它通常在回归的直线/平面上提供一个相关的推动。
可视化数据
我们将使用南加州大学马歇尔商学院网站上的广告数据。你可以在这里下载。
http://faculty.marshall.usc.edu/gareth-james/ISL/data.html
广告数据集包括产品在200个不同市场的销售情况,以及三种不同媒体(电视、广播和报纸)的广告预算。它是这样的
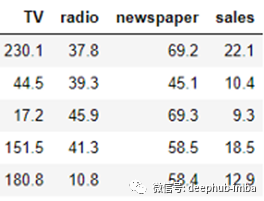
第一行数据显示,电视、广播和报纸的广告预算分别为230.1k美元、37.8k美元和69.2k美元,相应的销售量为22.1k(或22.1万)。
在简单的线性回归中,我们可以看到在不使用其他两种媒体的情况下,每一种广告媒体是如何影响销售的。然而,在实践中,这三者可能会共同影响净销售额。我们没有考虑这些媒体对销售的综合影响。
多元线性回归通过在一个表达式中考虑所有变量来解决这个问题。因此,我们的线性回归模型现在可以表示为:
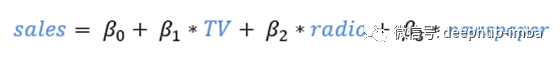
发现这些常数的值(β)是什么回归模型通过最小化误差函数,拟合最好的行或超平面(根据输入变量的数量)。这是通过最小化残差平方和( Residual Sum of Squares)来实现的,残差平方和是通过将实际结果和预测结果之间的差异平方得到的。
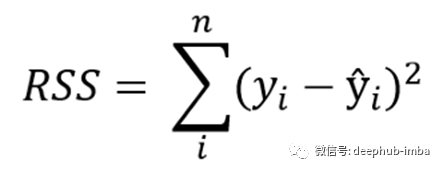
普通最小二乘法
因为这种方法求最小平方和,所以也称为普通最小二乘法(OLS)。在Python中,有两种主要的方法来实现OLS算法。
SciKit Learn:只需从Sklearn包中导入线性回归模块并将模型与数据匹配即可。这个方法非常简单,您可以在下面看到如何使用它。
from sklearn.linear_model import LinearRegressionmodel = LinearRegression()
model.fit(data.drop('sales', axis=1), data.sales)
StatsModels:另一种方法是使用StatsModels包来实现OLS。Statsmodels是一个Python包,允许对数据执行各种统计测试。我们将在这里使用它,以便您可以了解这个很棒的Python库,因为它将在后面的部分中对我们有帮助。
建立模型并解释系数
# Importing required libraries
import pandas as pd
import statsmodels.formula.api as sm# Loading data - You can give the complete path to your data here
ad = pd.read_csv("Advertising.csv")# Fitting the OLS on data
model = sm.ols('sales ~ TV + radio + newspaper', ad).fit()
print(model.params)
输出
Intercept 2.938889
TV 0.045765
radio 0.188530
newspaper -0.001037
Scikit Learn运行回归模型是最简单的方式,并且可以使用模型找到上面的参数。coef_ & model.intercept_。
现在我们有了这些值,如何解释它们呢?
- 如果我们确定电视和报纸的预算,那么增加1000美元的广播预算将导致销售增加189个单位(0.189*1000)。
- 同样地,通过固定广播和报纸,我们推断电视预算每增加1000美元,产品大约增加46个单位。
- 然而,对于报纸预算来说,由于系数几乎可以忽略不计(接近于零),很明显报纸并没有影响销售。事实上,它在0的负的一边(-0.001),如果幅度足够大,可能意味着这个代理是导致销售下降。但我们不能以如此微不足道的价值做出这种推断。
如果我们仅使用报纸预算与销售进行简单的线性回归,我们将观察到系数值约为0.055,这与我们上面看到的相比是非常显著的。为什么会这样呢?
共线性
ad.corr()
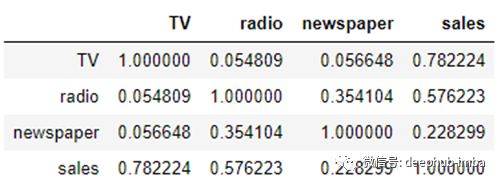
让我们用热图把这些数字形象化。
import matplotlib.pyplot as plt
%matplotlib inline> plt.imshow(ad.corr(), cmap=plt.cm.GnBu, interpolation='nearest',data=True)
> plt.colorbar()
> tick_marks = [i for i in range(len(ad.columns))]
> plt.xticks(tick_marks, data.columns, rotation=45)
> plt.yticks(tick_marks, data.columns, rotation=45)
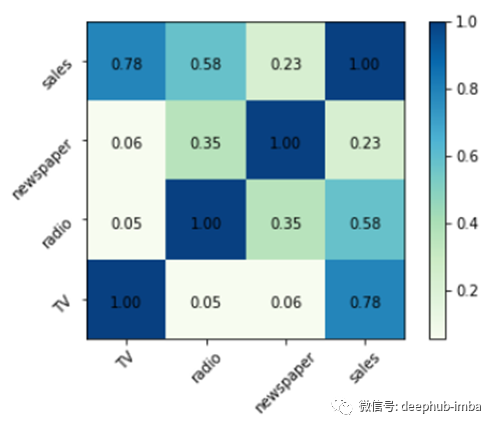
这里黑色的方块表示相关性很强(接近于1),而较亮的方块表示相关性较弱(接近于0)。这就是为什么所有的对角线都是深蓝色的,因为一个变量与它自己是完全相关的。
值得注意的是报纸和广播的相关性是0。35。这表明报纸和广播预算之间的关系是公平的。因此,可以推断出→当产品的广播预算增加时,在报纸上的花费也有增加的趋势。
这称为共线性,指的是两个或多个输入变量是线性相关的情况。
因此,尽管多元回归模型对报纸的销售没有影响,但是由于这种多重共线性和其他输入变量的缺失,简单回归模型仍然对报纸的销售有影响。
我们理解了线性回归,我们建立了模型,甚至解释了结果。到目前为止我们学的是线性回归的基础。然而,在处理实际问题时,我们通常会超越这一点,统计分析我们的模型,并在需要时进行必要的更改。
预测因子的假设检验
在运行多元线性回归时应该回答的一个基本问题是,至少有一个预测器在预测输出时是否有用。
我们发现,电视、广播和报纸这三个预测因子与销售额之间存在不同程度的线性关系。但是,如果这种关系只是偶然发生的,并且没有因为任何预测因素而对销售产生实际影响呢?
该模型只能给我们数字,以在响应变量和预测因子之间建立足够紧密的线性关系。然而,它无法证明这些关系的可信性。
我们从统计数据中获得帮助,并做一些被称为假设检验的事情。我们首先建立一个零假设和一个相应的备择假设。
因为我们的目标是找到至少一个预测器在预测输出时是否有用,所以我们在某种程度上希望至少有一个系数(不是截距)是非零的,这不仅仅是由于随机的机会,而是由于实际原因。为此,我们首先形成一个零假设:所有系数都等于零。
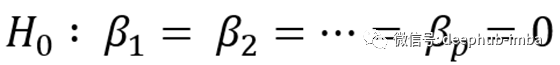
多元线性回归的一般零假设
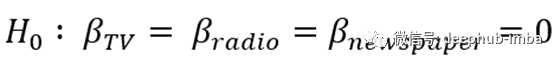
广告数据的零假设
因此,备择假设是:至少有一个系数不为零。通过发现有力的统计证据来拒绝原假设,从而证明了这一点
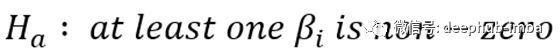
假设检验采用F-statistic进行。这个统计数据的公式包含残差平方和(RSS)和总平方和(TSS),我们不需要担心这一点,因为Statsmodels包会处理这个问题。我们在上面拟合的OLS模型的总结包含了所有这些统计数据的总结,可以用这行简单的代码得到:
print(model.summary2())
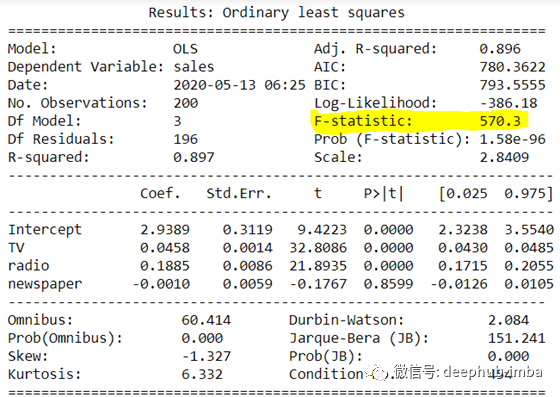
如果F-statistic的值等于或非常接近1,那么结果是支持零假设的,我们不能拒绝它。
但是我们可以看到,F-statistic比1大很多倍,因此为零假设(所有系数都为零)提供了有力的证据。因此,我们拒绝原假设,并相信至少有一个预测器在预测输出时是有用的。
注意,当预测因子(p)的数量很大,或者p大于数据样本的数量(n)时,f统计量是不合适的。
因此,我们可以说,在这三家广告代理商中,至少有一家在预测销售额方面是有用的。
但是哪一个或哪两个是重要的呢?它们都重要吗?为了找到这一点,我们将执行特征选择或变量选择。一种方法是尝试所有可能的组合。
- Only TV
- Only radio
- Only newspaper
- TV & radio
- TV & newspaper
- radio & newspaper
- TV, radio & newspaper
在这里,尝试所有7种组合仍然是可行的,但是如果有更多的预测因子,组合的数量将呈指数增长。例如,通过在我们的案例研究中再增加一个预测因子,总组合数将变为15。想象一下有一打预测器。因此,我们需要更有效的方法来执行特性选择。
特征选择
做特征选择的两种最流行的方法是:
正向选择:我们从一个没有任何预测器的模型开始,只使用截距项。然后,我们对每个预测器执行简单的线性回归,以找到最佳执行器(最低RSS)。然后我们添加另一个变量,并再次通过计算最低的RSS(残差平方和)来检查最佳的2变量组合。然后选择最佳的3变量组合,以此类推。当满足某种停止规则时,停止该方法。
逆向选择:我们从模型中的所有变量开始,然后删除统计意义最小的变量(更大的p值:检查上面的模型摘要,找到变量的p值)。重复此操作,直到达到停止规则为止。例如,我们可以在模型分数没有进一步提高的时候停止。
在这篇文章中,我将介绍向前选择方法。首先,让我们了解如何选择或拒绝添加的变量。
我们要使用2种方法来评估我们的新模型:RSS和R²。
我们已经熟悉RSS,它是残差平方和,通过将实际输出和预测结果之间的差平方来计算。它应该是模型表现良好的最小值。R²方差的程度的测量数据是用模型来解释。
数学上,它是实际结果和预测结果之间相关性的平方。R²接近1表明模型是好的和解释方差数据。接近于零的值表示模型很差。
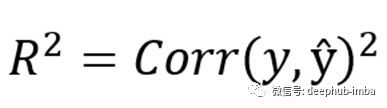
# Defining a function to evaluate a model
def evaluateModel(model):
print("RSS = ", ((ad.sales - model.predict())**2).sum())
print("R2 = ", model.rsquared)
让我们首先使用单个预测器逐个评估模型,从TV开始。
# For TV
model_TV = sm.ols('sales ~ TV', ad).fit()
evaluateModel(model_TV)
RSS = 2102.5305831313512
R^2 = 0.611875050850071
# For radio
model_radio = sm.ols('sales ~ radio', ad).fit()
evaluateModel(model_radio)
RSS = 3618.479549025088
R^2 = 0.33203245544529525
# For newspaper
model_newspaper = sm.ols('sales ~ newspaper', ad).fit()
evaluateModel(model_newspaper)
RSS = 5134.804544111939
R^2 = 0.05212044544430516
我们观察到model_TV, RSS和R²最小值是最在所有的模型。因此,我们选择model_TV作为向前基础模型。现在,我们将逐个添加广播和报纸,并检查新值。
# For TV & radio
model_TV_radio = sm.ols('sales ~ TV + radio', ad).fit()
evaluateModel(model_TV_radio)
RSS = 556.9139800676184
R^2 = 0.8971942610828957
正如我们所看到的,我们的价值观有了巨大的进步。RSS下降和R²进一步增加,model_TV相比。这是个好兆头。现在我们来看看电视和报纸。
# For TV & newspaper
model_TV_radio = sm.ols('sales ~ TV + newspaper', ad).fit()
evaluateModel(model_TV_newspaper)
RSS = 1918.5618118968275R^2 = 0.6458354938293271
报纸的加入也提高了报纸的价值,但不如广播的价值高。因此,在这一步,我们将继续电视和广播模型,并将观察当我们添加报纸到这个模型的差异
# For TV, radio & newspaper
model_all = sm.ols('sales ~ TV + radio + newspaper', ad).fit()
evaluateModel(model_all)
RSS = 556.8252629021872
R^2 = 0.8972106381789522
这些值没有任何显著的改进。因此,有必要不添加报纸,并最终确定模型与电视和广播作为选定的功能。所以我们最终的模型可以表示为:
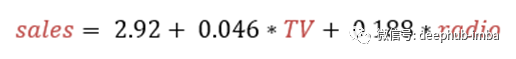
在3D图形中绘制变量TV、radio和sales,我们可以可视化我们的模型如何将回归平面与数据匹配。
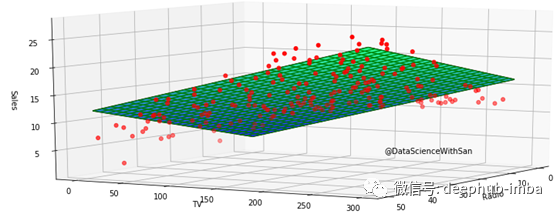
希望看完这篇文章后你会对多元线性回归有一个新的理解。
DeepHub
微信号 : deephub-imba
每日大数据和人工智能的重磅干货
大厂职位内推信息
长按识别二维码关注 ->
好看就点在看!********** **********