第3章 Stata描述统计

    在进行数据分析时，当研究者得到的数据量很小时，可以通过直接观察原始数据来获得所有的信息。但是当得到的数据量很大时，就必须借助各种描述指标来完成对数据的描述工作。用少量的描述指标来概括大量的原始数据，对数据展开进行描述的统计分析方法被称为描述性统计分析。本章将会为大家介绍的描述性统计分析方法包括定距变量的描述性统计、正态性检验和数据转换、单个分类变量的汇总、两个分两类变量的列联列表分析、多表和多维列连列表分析。

3.1定距变量的描述性统计

    数据分析中大部分变量都是定距变量，通过进行定距变量的基本描述性统计，我们可以得到数据得概要统计指标，包括平均值、最大值、最小值、标准差、百分位数、中位数、偏度系数和峰度系数等。数据分析者通过或者这些指标，可以从整体上对拟分析的数据进行宏观的把握，从而为后续进行更深入的数据分析做好必要的准备。

    数据（案例3.1）时我国电力消费情况。试通过对数据进行基本描述性分析来了解我国各地区电力消费的基本情况。变量为地区和电力消费量

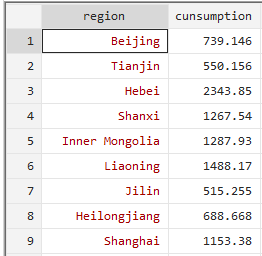
summarize cunsumption

    我们可以看到一共有31个样本参与了分析，电力消费量的平均值时1180.489，样本的标准差时903.5561，样本最小值时17.6987，样本最大值时3609.642。

案例延伸

1.获得更详细的描述性统计结果

sum cunsumption,detail

    从上图我们可以得到更加详细的信息。

    （1）百分位数（Percentiles）

    可以看出数据的第一个四分位数（25%）时550.1556，数据的第二个四分位数（50%）是891.1902，数据的第三个四分位数（75%）是1324.61，数据的百分位数的含义是低于该数据值得样本在全体样本中得百分比。例如，本例中25%分位数得含义是全体样本中有25%得数据值低于550.1556。

    （2）四个最小值（Smallest）

    本例中，最小的四个数据分别是17.6987、133.7675、337.2368、462.9585。

    （3）四个最大值（Largest）

    本例中，最大的四个数据分别是3609.642、3313.986、2941.067、2471.438。

    （4）平均值（Mean）和标准差（Std.Dev）

    （5）偏度（Skewness）和峰度（Kurtosis）

    偏度的概念是表示不对称的方向和程度。如果偏度值大于0，那么数据就具有正片都（右边有尾巴）；如果偏度值小于0，那么数据就具有负偏度（左边有尾巴）；如果偏度值等于0那么数据将呈对称分布。本例中，数据偏度为1.309032，为正偏度但不大。

    峰度概念用来表示尾重，是正太分布结合在一起考虑的。正态分布是一种对称的分布，他的峰度值正好等于3，如果某数据的峰度大于3，那么该分布将会有一个比正态分布更长的尾巴，如果某数据的峰度值小于3，那么该分布将会有一个比正态分布更短的尾巴。本例中，数据峰度为3.889152，有一个比正态分布更长的尾巴。

2.根据自己的需要或去相应的概要统计指标

tabstat cunsumption,stats(mean range sum var)

    从上图我们可以得知，数据的平均值是1180.489，极差是3591.944，总和是36595.15，方差是816413.7。

    统计量与其对应的命令代码如表3.2所示

统计量命令代码统计量命令代码统计量命令代码均值mean非缺失值总数count计数n总和sum最大值max最小值min极差range标准差sd方差var变异系数cv标准误semean偏度skewness峰度kuitosis中位数median第一个百分位数pl四分位距iqr四分位数q

3.按另一变量分类列出某变量的概要统计指标

tabstat cunsumption ,stats(mean range sum var) by(region)

4.创建变量总体均值的置信区间

ci mean cunsumption,level(98)

    基于本例中的观测样本，我们可以推断出总体98%水平的置信区间。也就是我们我有98%的信心可以认为数据总体的均值或落在【781.7159，1579.262】中，或者说，数据总体的均值落在区间【781.7159，1579.262】的概率是98%。我们可以调整括号里面的数字来调整置信水平的大小。

3.2正态性检验和数据转换

    很多统计程序对于数据的要求是比较严格的，他们只有在变量服从或者近似正态分布的时候才是有效的，所以在对整理收集的数据进行预处理的时候需要对他们进行正态分布检验，如果数据不满足正态分布假设，我们就要对数据进行必要的转换。数据转换分为线性转换和非线性转换两种。线性转换比较简单我们在第一章中有所涉及。本章主要讲的是非线性的转换。

    数据（案例3.2）是我国各地区的公共交通的运营情况，某课题组搜子整理了我国2009年各省市公共交通车辆运营的数据。（1）对数据进行正态分布检验（2）对数据执行平方根变换方法，以或去新的数据进行正态分布检验（3）对数据执行自然对数变换方法，以获取新的数据斌进行正态分布检验。变量有两个一个地区一个交通车辆运营数。

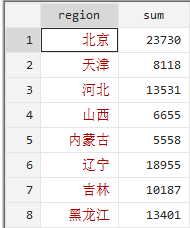
sktest sum #本命令是对数据进行正态分布检验

    上图我们可以明显的看到，sktest命令拒绝了数据呈正态分布的假设，从偏度（Pr(Skewness)=0.0065）上来看，小于0.05，拒绝正态分布的原假设；从偏度上来看（Pr(Kurtosis)=0.0804），大于 0.05，接受正态分布的原假设；但是把两者结合在一起考虑，从整体上来看Prob>chi2=0.0123，小于0.05，拒绝正太分布假设。

generate srsum=sqrt(sum) #本命令是对数据执行平方根变换方法，以获取新的数据进行正态分布检验
sktest srsum

    结果不再过多赘述，我们可以看到变换后的数据是接受了呈正太分布的原假设。

gen lsum=ln(sum) #本命令是对数据执行自然对数变换方法，获取新的数据进行正态分布检验
sktest lsum

    结果不再过多赘述，我们可以看到总体上变换后的数据是接受了正态分布的原假设。

案例延伸

1.有针对性地对数据进行变换

    我们在进行数据分析师，在对初始数据进行正态性检验之后，可以利用3.1节地相关知识得到关于数据偏度和峰度地信息，我们完全可以根据数据新的偏态特征进行有针对性地数据变换。数据变换与其对应地命令如下表所示：

Stata命令数据转换效果gen y=x^3立方减少严重负偏态gen y=x^2平方减少轻度负偏态gen y=sqrt(x)平方根减少轻度正偏态gen y=ln(x)自然对数减少轻度正偏态gen y=log10(x)以10为底地都对数减少正偏态gen y=-(sqrt(x))平方根负对数减少严重正偏态gen y=-(x^-1)负倒数减少非严重正偏态gen y=-(x^-2)平方负倒数减少非严重正偏态gen y=-(x^-3)立方负倒数减少非严重正偏态

2.关于ladder命令介绍

    此处我们介绍一个非常好用地命令：ladder。他把幂阶梯和正态分布检验有校地结合到了一起。它尝试幂阶梯上地每一种幂并逐个反馈结果是否显著地为正态或者非正态。

ladder sum

    我们可以非常轻松地看出，在95%的置信水平上，仅有平方根变化和自然对数变化是符合正态分布的，其他幂次的数据变换都不能使数据呈现正态分布。

3.关于gladder命令的介绍

gladder sum

    我们可以非常轻松的看出每种转换的直方图与正态分布曲线。与延伸2得出的结论是一致的。

3.3单个分类变量的汇总

    与前面提到的定距变量不同，分类变量的数值只代表观测值所属的类，不代表其他任何含义。因此，对分类变量的描述统计方法观察是不同类别的频数或者百分数。

    数据（案例3.3）是某国有银行沈阳分行人力资源部对分行本部在岗职工的结婚情况进行了调查。调查结果分为了两类，一类为已婚，一类为未婚或者离异。试对结婚情况这一变量进行单个变量汇总。

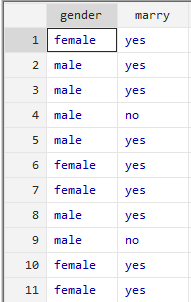
tabulate marry

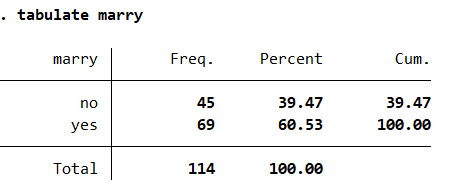
    从分析结果中我们可以看出本部一共有114人参与了调查，其中处于结婚状态的有69名员工占比60.53%处于非结婚状态的有45名员工占比39.47%。此外，结果分析栏中Cum表示的是累计百分比。

案例延伸

    试对结婚状况这一变量进行单个变量汇总并附有星点图。

tabulate marry,plot

3.4两个分类变量的列联列表分析

    在上节中我们讲述了单个分类变量的概要统计，这次我们将二位列联表

    数据（案例3.4）是某课题组对A市居民的吸烟喝酒状况进行调查研究，试对该数据进行二位列联表分析。变量分别为性别 吸烟与否 喝酒与否

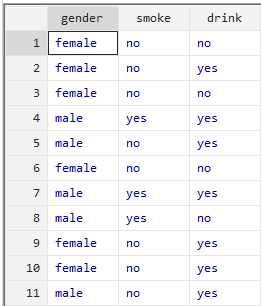
tabulate smoke drink

    从分析结果中我们可以看出本次调查所获得的信息；共有124为A市民参与了调查，其中抽烟的有68人不抽烟的有56人，有41人喝酒83人不喝酒，只吸烟不喝酒的有39人，只喝酒不吸烟的有12人。

案例延伸

    显示每个单元格的列百分比与行百分比

tabulate smoke drink,column row

    结果包含了三部分，第一行表示的聘书，第二行表示的是行百分比，第三行表示的列百分比。例如最左上角单元格的意义是：不吸烟也不喝酒的样本个数有44个，这部分在不吸烟的样本中占比78.57%、在所有不喝酒的样本中占比53.01%。

3.5多表和多维列联分析

    数据（案例3.5）是某高校经济学院针对其研究生学生的持有证书情况进行了调查。证书分为三类，包括会计证、审计师、经济师。试用stata对数据进行一下操作（1）对数据中的所有分类变量进行单个变量统计汇总（2）对数据中的所有分类变量进行二位列联表分析（3）以是否持有会计证为主分类变量，制作三个分类变量的三位列联表

tab1 account audit economy #本命令的含义是对数据中的所有分类变量进行单个变量汇总统计

    结果不再过多赘述。

tab2 account audit economy #本命令的含义是对数据中所有分类变量进行二位列联表分析

    结果不再过多赘述。

by account,sort:tabulate audit economy #本命令的含义是以是否持有会计证为主分类变量，制作的三个分类变量的三维列联表

    结果不再过多赘述。

案例延伸

    实现多种数据的聘书、标准差数据特征的列联分析。

table account audit economy,contents(freq)

    结果不再赘述。上述命令中contents括号里的内容表示频数，该括号内支持的内容与命令符号的对应关系如下图。

命令符号括号内支持的内容命令符号括号内支持的内容freq频数min xx的最小值sd xx的标准差median xx的中位数count xx非缺失观测值的计数mean xx的平均数max xx的最大值rawsum x忽略任意规定权数的总和sum xx的总和iqr xx的四分位距n xx非缺失观测值的计数pl xx的第一个百分位数