线性规划之内点法

1.内点法是在可行域内部进行搜索，最后收敛到最优解边界

2.常用的内点法有仿射尺度法、对数障碍法和原始对偶法

线性规划（LP）问题除了用单纯形法和对偶理论来求解，还有一种搜索的解法——内点法（interior point method），它是在可行域内部移动。今天我们来学习三种内点法，包括：仿射尺度法（affine-scaling），对数障碍法（log-barrier）和原始对偶法（primal-dual）.

同样的，为了便于介绍，我们引进一个新例子——弗兰妮的木柴：

每年弗兰妮从她的小树林里卖出3根火柴。一个潜在顾客愿意支付每半根90美元，另一位愿意支付每根150美元。我们的问题是弗兰妮应该卖给每位顾客多少木柴以最大化自己的收益？假设每位顾客可以尽可能多地购买。

对上述情景建立模型，很容易得到：

在二维坐标轴画出它的可行域区域。

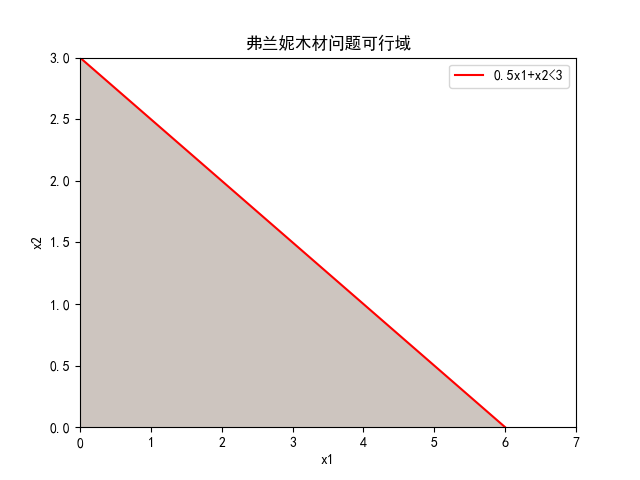
0

内点法的逻辑

内点法是在可行域内部进行搜索迭代的****算法，它有一个显著的优点：没有约束起作用，所有方向都是可行的。但我们知道最大化模型的最大改进方向是梯度方向，最小化模型的最大改进方向是负梯度方向。这样子内点法就不可避免的会在边界点停下。假设弗兰妮木材问题，从内点X0(1,0.5)往梯度方向改进，根据最大步长原理，下一个点会停留在可行域边界上X1：

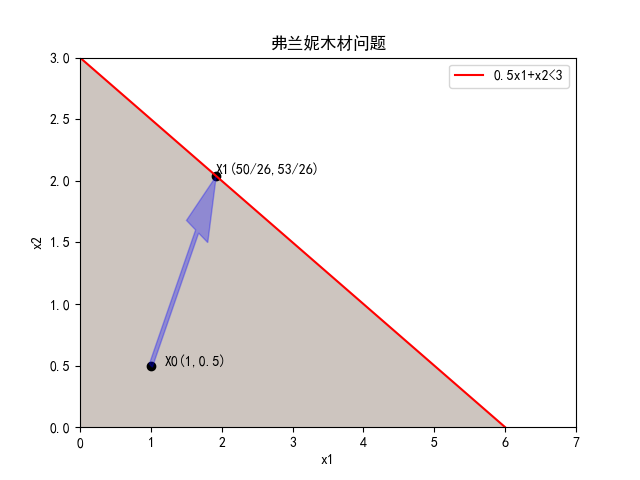
因此，内点法的关键在于，搜索点是否一直保持在可行域的“中部”指导最优解被找到，其要遵循：内点法从一个内部可行点开始，并且在一系列内部点之间进行搜索，直到最优解处收敛到可行域的边界。

要检查每次迭代点是否为内点，我们先要将LP问题变为标准型的线性规划，已弗兰妮木柴问题为例：

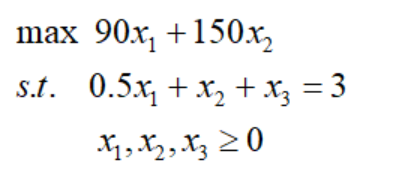
这样就很容易判断一个可行解是否为内点：给定线性规划标准型的可行解，若可行解每一个分量都严格为正，则该可行解是一个内点

下面举个例子加以说明：

可以看到，对于标准型LP问题，内点必须满足：约束条件Ax=b成立；分量严格大于0。它的下一个搜索点的方向要满足：

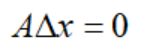
根据投影理论，我们可以得到内点的移动方向：

通常来说，取d是正负梯度方向，因为该方向是改进最快的方向，Δx保证了可行方向。上面的理论表明移动方向尽可能靠近改进方向且保持在内点上。那么Δx是否为改进方向呢，答案是肯定的，我们可以证明：

举个例子：

总结一下，内点法的核心是找到最优解以前避开可行域的边界，并保证每一轮迭代都是可行改进方向。

1

仿射尺度算法

根据上一节的原理，我们提出一种避开边界的有效工具——尺度变换（scaling），首先定义当前解的对角方阵形式：

因为内点的分量严格大于0，由此我们构建仿射尺度变换（affine scaling）和逆仿射尺度变换：

经过变换，会改变原本标准型线性规划的形式：

以弗兰妮木柴问题为例，c=(90,150,0),A=(0.5,1,1),b=(3)，则：

仿射尺度变换后的形式，要得到下一个搜索点，根据投影理论，我们得到：

利用逆仿射尺度变换可以得到原目标函数的可行改进方向Δx：

接下来就剩下最后一个问题，移动的步长是多少：

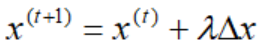
很显然，我们要严格保证每一步得到的解每个分量都严格大于0，直至收敛到最优解。对于最大化问题，如果Δx非负，则对应的标准型线性规划模型无界。否则：

为什么是这样呢，因为经过仿射尺度变换后的y，均为1：

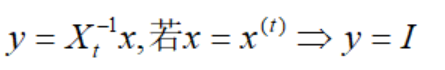
说明搜索范围在一个单位圆（维度n）内进行，只需要通过找出这种球形的极限来实现仿射尺度变换。

综上，我们得到仿射尺度算法****的步骤：

以弗兰妮木柴问题为例，我们来看看仿射尺度变换算法的细节：

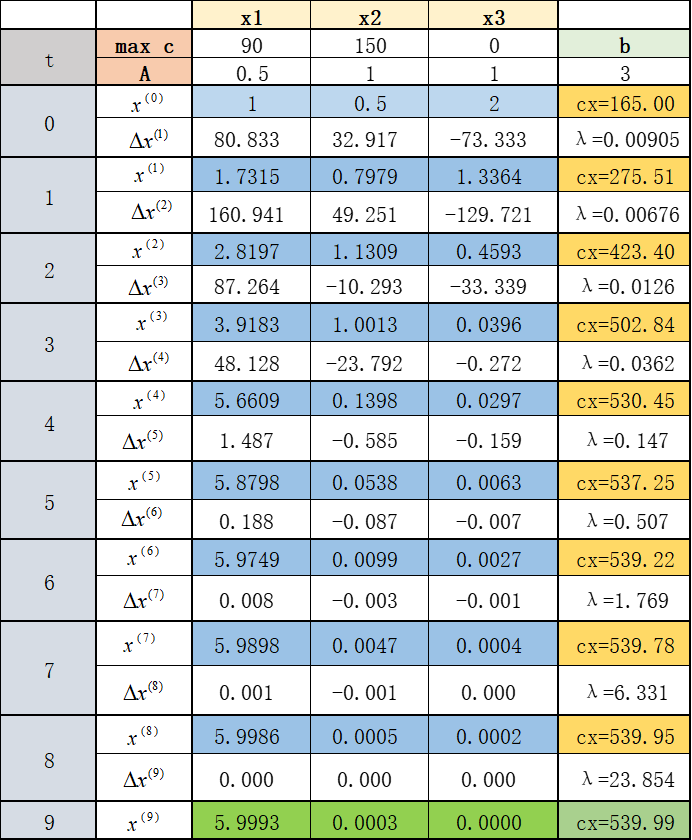
可以看到，迭代到第九次的时候，误差已经很接近最优解了。我们利用python程序可以轻松实现这个过程：

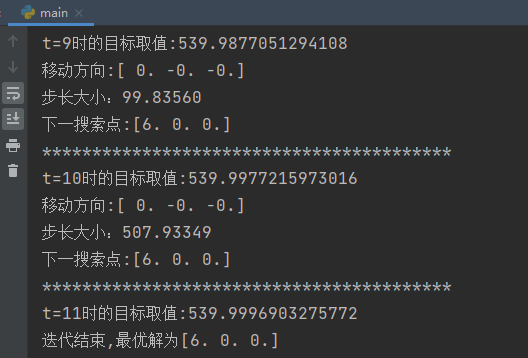
下面3D图展示了搜索过程（只展示前6次迭代）：

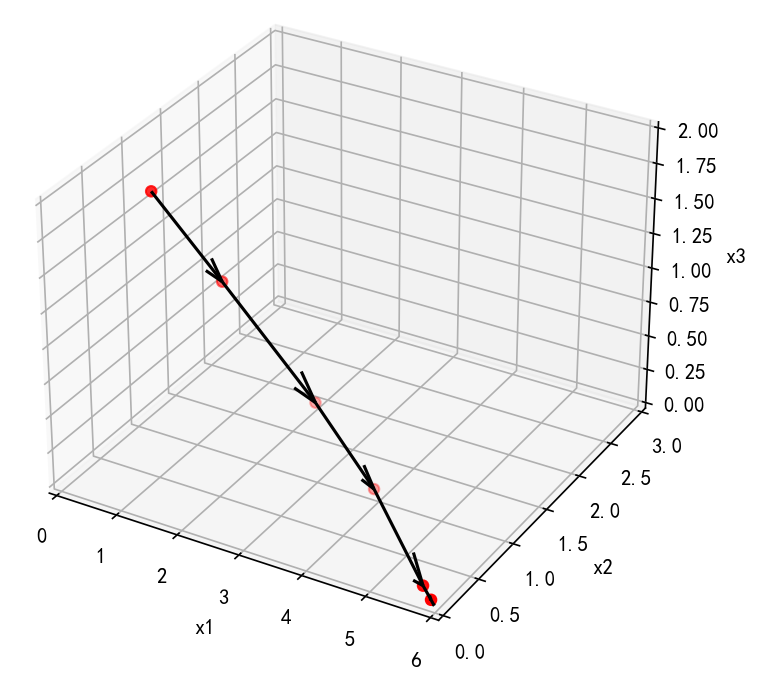
二维图更加精确的展示了搜索过程均在可行域的内点进行：

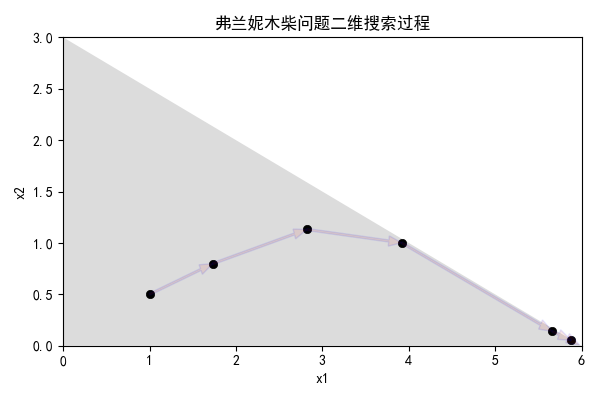
注：代码放到附录

2

对数障碍法

下面我们介绍第二种内点法——对数障碍法。先直接给出模型：

这里的思想也是尽可能使得搜索点原理边界，为什么这样呢，因为：

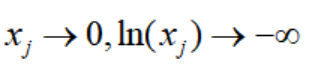
以弗兰妮木柴问题为例：

可以看到越接近边界，障碍项对真实值的影响越显著，这样就避免了搜索算法在迭代中触及可行域边界。

拥有对数障碍项的规划问题是非线性的，我们利用牛顿法的思想，在多元函数上进行二阶泰勒展开进行迭代，推导过程不再展开，这里直接给出移动的方向：

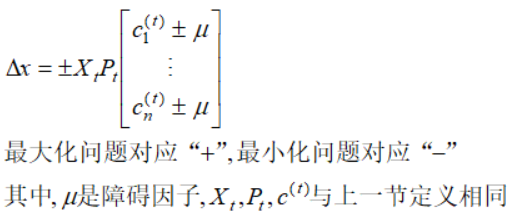
从牛顿迭代的障碍法的步长为：

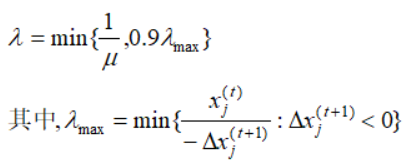
上述公式，倍数定位0.9是因为由于目标的非线性，搜索过程可能接近步长最大值以前就停止改进，或者可能是在当前解附近改进方向在更大步长之后开始降低目标函数值。

接下来剩余最后一个问题——障碍因子的确定。很显然，该因子较大时对接近边界的内点阻碍作用显著，较小时鼓励搜索过程接近边界。因此，障碍算法通常以较大的因子开始，随着搜索过程的进行缓慢将其减小到0

综合以上，我们得到障碍算法的步骤：

依旧以弗兰妮木柴问题为例，用代码实现这个过程，下图展示了前五次二维搜索过程：

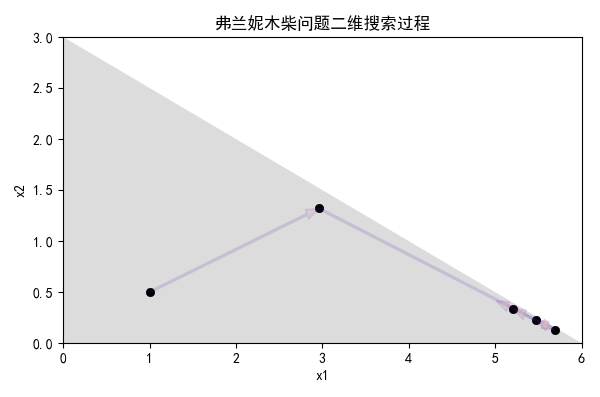
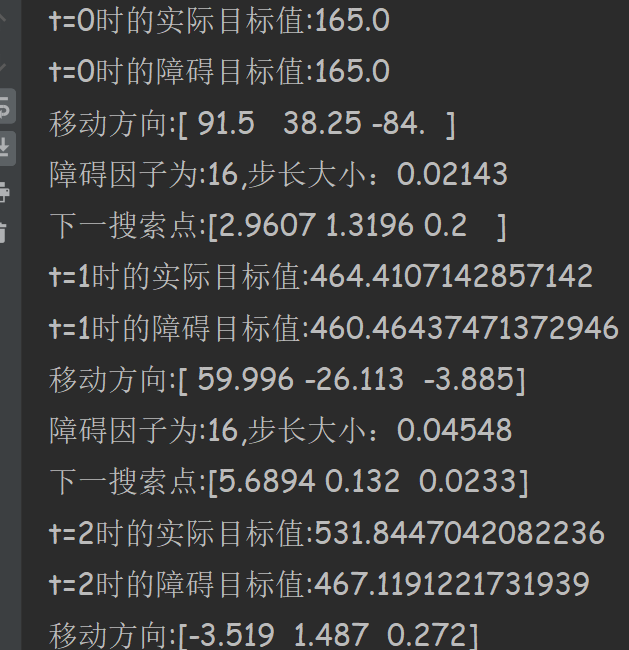
小编开发的代码经历12次迭代达到最优，下面是部分截图，代码见附录。

3

原始对偶法

本节我们讨论内点法的最后一种算法——原始对偶内点法。在对偶理论里面，我们得到了标准型原始问题与对偶问题的形式以及松弛条件：

传送门：线性规划的对偶理论

我们将对偶问题加上松弛变量，化成不含不等式约束的形式，得到：

在最优解处,我们有：

如果解不是在最优处，上面的等式不满足，而原始对偶内点法（primal-dual interior-point search）利用它们的对偶间隙（duality gap）进行迭代：

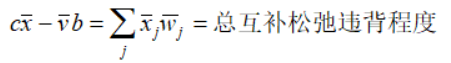
迭代原理是：原始对偶内点法始终保持原始问题和对偶问题的解在每次迭代中严格可行，并在搜索过程中系统性减小互补松弛性的违背程度

具体的，原始对偶内点法在搜索中给每个违背程度设定目标μ>0,寻找能够减小当前的互补松弛结果与目标差异的可行移动方向，并且逐渐减少μ到0，实现互补松弛，这需要：

接下来剩下最后一个问题：步长λ的确定。算法通过调整一个正的障碍因子（boundary prevention）——常数δ使得搜索过程保持在可行域内部

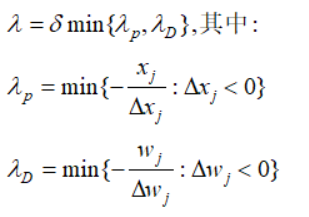
综上，我们得到原始对偶内点法的步骤：

该算法我们这里不做实现，以后会结合对偶理论一起出实现代码！今天就先结束吧，祝国庆快乐！！

【附录】：

#放射尺度变换
import sys
import numpy as np

c = np.array([90,150,0])
A = np.array([0.5,1,1])
# D = []
t = 0
x_t = np.array([1,0.5,2])
while True:
    # D.append(list(x_t))
    print('t={}时的目标取值:{}'.format(t,np.dot(c,x_t)))
    for i in list(x_t):
        if round(i,6) == 0:
            print('迭代结束,最优解为{}'.format(np.around(x_t,4)))
            sys.exit()
    X_t = np.diag(x_t)
    c_t = np.dot(c,X_t)
    A_t = np.dot(A,X_t)
    P_t = np.identity(3) - np.dot(A_t.reshape(3,1),A_t.reshape(1,3))/np.dot(A_t,A_t.T)
    delat_x = np.dot(X_t,np.dot(P_t,c_t))
    print('移动方向:{}'.format(np.around(delat_x,2)))
    a = np.dot(delat_x,np.linalg.inv(X_t))
    lam = 1/np.sqrt(np.dot(a,a))
    print('步长大小：{:.5f}'.format(lam))
    x_t = x_t + lam*delat_x
    print('下一搜索点:{}'.format(np.around(x_t,4)))
    t += 1
#     D.append(list(delat_x))
    print('*****************************************')

#对数障碍法
import numpy as np
import pandas as pd
c = np.array([90,150,0])
A = np.array([0.5,1,1])
D = []
t = 0
x_t = np.array([1,0.5,2])
y = 0
u = 16
while True:
    D.append(list(x_t))
    y_old = np.dot(c, x_t)+u*np.sum(np.log(x_t))
    print('t={}时的实际目标值:{}'.format(t,np.dot(c,x_t)))
    print('t={}时的障碍目标值:{}'.format(t, y_old))
    X_t = np.diag(x_t)
    c_t = np.dot(c,X_t)
    A_t = np.dot(A,X_t)
    P_t = np.identity(3) - np.dot(A_t.reshape(3,1),A_t.reshape(1,3))/np.dot(A_t,A_t.T)
    delat_x = np.dot(np.dot(X_t,P_t),c_t+u)
    print('移动方向:{}'.format(np.around(delat_x,3)))
    lam_list = []
    for i in range(3):
        if delat_x[i] < 0:
            lam_list.append(-0.9*x_t[i] / delat_x[i])
    lam = min(1/u,min(lam_list))
    print('障碍因子为:{},步长大小：{:.5f}'.format(u,lam))
    x_t = x_t + lam*delat_x
    print('下一搜索点:{}'.format(np.around(x_t,4)))
    y_new = np.dot(c, x_t)+u*np.sum(np.log(x_t))
    t += 1
    if y_new - y_old < 1:
        if u < 0.5:
            print('迭代结束,最优解为{}'.format(np.around(x_t, 2)))
            break
        else:
            u = u/2
    else:
        continue
#     D.append(list(delat_x))
    print('*****************************************')

import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
fig = plt.figure(figsize=(12,6))
ax = plt.axes(projection='3d')
ax.scatter(A['x1'],A['x2'],A['x3'],color='red',s=25)
ax.quiver(A['x1'],A['x2'],A['x3'],A['u'],A['v'],A['w'],arrow_length_ratio=0.2,color='black')
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel('x3')
ax.set_xlim(0,6)
ax.set_ylim(0,3)
ax.set_zlim(0,2)
ax.set_title('弗兰妮木柴问题搜索过程')
plt.show()

plt.figure(figsize=(6,4))
plt.fill_between(np.linspace(0,6,500),np.tile(np.array(0),500),3-0.5*np.linspace(0,6,500),facecolor="#DCDCDC")
plt.scatter(A['x1'],A['x2'],color='black',linewidths=0.5)
# plt.text(-6,-1,s='X0(-5,0)',verticalalignment='bottom')
for _,row in A.iterrows():
    plt.arrow(row.x1, row.x2, row.u, row.v, length_includes_head=True, head_width=0.1, width=0.02, alpha=0.1, fc='#CD2626', ec='blue')

plt.xlim(0,6)
plt.ylim(0,3)
plt.xlabel("x1")
plt.ylabel("x2")
plt.title("弗兰妮木柴问题二维搜索过程")
plt.tight_layout()
plt.show()