Datawhale X 李宏毅苹果书AI夏令营 Task3学习笔记

批量归一化

    误差表面往往是粗糙的，为了方便训练，往往需要“铲平”。**批量归一化**就是其中的一个方法。

    当输入的特征，每一个维度的值，它的范围差距很大的时候，就可能产生不同方向，斜率非常不同，坡度非常不同的误差表面。如果我们可以给不同的维度，同样的数值范围的话，那我们可能就可以制造比较好的误差表面。

    让训练变得比较容易一点其实有很多不同的方法，这些不同的方法往往就合起来统称为**特征归一化**。

特征归一化的一种可能性： Z 值归一化

•    *假设 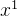![x^{1}](https://latex.csdn.net/eq?x%5E%7B1%7D) 到 ![x^{R}](https://latex.csdn.net/eq?x%5E%7BR%7D)，是我们所有的训练数据的特征向量。我们把所有训练数据的特征向量，统统都集合起来。向量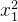 ![x_{1}^{}](https://latex.csdn.net/eq?x_%7B1%7D%5E%7B%7D) 里面就![x_1^1](https://latex.csdn.net/eq?x_1%5E1) 代表 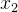![x_{1}^{}](https://latex.csdn.net/eq?x_%7B1%7D%5E%7B%7D) 的第一个元素，![](https://latex.csdn.net/eq?)![x_1^2](https://latex.csdn.net/eq?x_1%5E2) 代表 ![x_2](https://latex.csdn.net/eq?x_2) 的第一个元素，以此类推。我们把不同笔数据即不同特征向量，同一个维度里面的数值，把它取出来，对于每个维度 i，计算其平均值 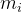![m_i](https://latex.csdn.net/eq?m_i) 和标准差 σ![_i](https://latex.csdn.net/eq?_i)。接下来我们就可以做一种归一化:
  
    ![\widetilde{x}_i^r \leftarrow \frac{x_i^r-m_i}{\delta ^i}](https://latex.csdn.net/eq?%5Cwidetilde%7Bx%7D_i%5Er%20%5Cleftarrow%20%5Cfrac%7Bx_i%5Er-m_i%7D%7B%5Cdelta%20%5Ei%7D)
  

    就是把这边的某一个数值x，减掉这一个维度算出来的平均值，再除掉这个维度，算出来的标准差，得到新的数值 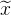![\widetilde{x}](https://latex.csdn.net/eq?%5Cwidetilde%7Bx%7D)。得到新的数值以后，再把新的数值把它塞回去。

    做完归一化以后，这个维度上面的数值就会平均是 0，其方差是 1，所以这一排数值的分布就都会在 0 上下；对每一个维度都做一样的归一化，所有特征不同维度的数值都在 0 上下，可能就可以制造一个比较好的误差表面。所以像这样子的特征归一化方式往往对训练有帮助，它可以让在做梯度下降的时候，损失收敛更快一点，训练更顺利一点。

考虑深度学习

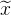    ![\widetilde{x}](https://latex.csdn.net/eq?%5Cwidetilde%7Bx%7D)代表归一化的特征，把它丢到深度网络里面，去做接下来的计算和训练。

    虽然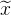![\widetilde{x}](https://latex.csdn.net/eq?%5Cwidetilde%7Bx%7D)已经做归一化了，但是通过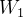![W_1](https://latex.csdn.net/eq?W_1)以后，没有做归一化,它的数值的分布仍然有很大的差异。对于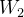![W_2](https://latex.csdn.net/eq?W_2)，a或z其实也是一种特征，也应该要对这些特征做归一化（比较推荐对z做）。

接下来计算标准差

最后，根据计算出的 µ 和 σ 进行归一化：

    产生了一个问题：因为训练数据非常多，现在一个数据集可能有上百万笔数据，GPU 的显存无法把它整个数据集的数据都加载进去。因此，在实现的时候，我们不会让这一个网络考虑整个训练数据里面的所有样本，而是只会考虑一个批量里面的样本。这个时候就不需要对整个数据集做特征归一化，而改成只在一个批量上做特征归一化作为近似。

测试时的批量归一化

    在测试的时候，我们一次会得到所有的测试数据，确实也可以在测试的数据上面，制造一个一个批量。但是假设系统上线，做一个真正的线上的应用，比如批量大小设 64，我一定要等 64 笔数据都进来，才做一次做运算，这显然是不行的。

    **移动平均：**假设现在有各个批量计算出来的 µ1, µ2, µ3, · · · · · · , µt，则可以计算移动平均

    测试的时候，在真正应用上也没有批量，就可以就直接拿µ¯ 跟 σ¯ ，也就是 µ,σ 在训练的时候，得到的移动平均来取代原来的 µ 跟 σ，如图 3.45 所示，这就是批量归一化在测试的时候的运作方式。

内部协变量偏移

    假设网络有很多层，-x 通过第一层后得到 a，a 通过第二层以后得到 b；计算出梯度以后，把 A 更新成 A′，把 B 这一层的参数更新成 B′。作者认为，我们在计算 B 更新到 B′ 的梯度的时候，这个时候前一层的参数是 A，或者是前一层的输出是 a。那当前一层从 A 变成 A′ 的时候，其输出就从 a 变成 a′ 。但是我们计算这个梯度的时候，是根据 a 算出来，所以这个更新的方向也许它适合用在 a 上，但不适合用在 a′ 上面。因为我们每次都有做批量归一化，就会让 a 和a′ 的分布比较接近。

卷积神经网络

    卷积神经网络主要用于图像分类任务。怎么把图像当做模型的输入呢？对于机器，图像可以描述为三维张量。一张图像是一个三维的张量，其中一维代表图像的宽，另外一维代表图像的高，还有一维代表图像的通道的数目。

Q：什么是通道？A：彩色图像的每个像素都可以描述为红色、绿色、蓝色的组合，这 3 种颜色就称为图像的 3 个色彩通道。这种颜色描述方式称为 RGB 色彩模型，常用于在屏幕上显示颜色。

    模型的弹性越大，就越容易过拟合。为了避免过拟合，在做图像识别的时候，考虑到图像本身的特性，并不一定需要全连接，即不需要每个神经元跟输入的每个维度都有一个权重。接下来就是针对图像识别这个任务，对图像本身特性进行一些观察。

    模型的输出应该是什么呢？模型的目标是分类，因此可将不同的分类结果表示成不同的独热向量 y′。在这个独热向量里面，类别对应的值为 1，其余类别对应的值为 0。

第 1 个观察：检测模式不需要整张图像

    人在判断一个物体的时候，往往也是抓最重要的特征。看到这些特征以后，就会直觉地看到了某种物体。对于机器，也许这是一个有效的判断图像中物体的方法。但假设用神经元来判断某种模式是否出现，也许并不需要每个神经元都去看一张完整的图像。因为并不需要看整张完整的图像才能判断重要的模式是否出现。只需要把图像的一小部分当作输入，就足以让它们检测某些特别关键的模式是否出现，这是第 1 个观察。

感受野

    卷积神经网络会设定一个区域，即**感受野**，每个神经元都只关心自己的感受野里面发生的事情，感受野是由我们自己决定的。

    我们没有办法检测所有的模式，所以同个范围可以有多个不同的神经元，即多个神经元可以去守备同一个感受野。常见的感受野设定方式就是核大小为 3 × 3。

    感受野超出了图像的范围，怎么办呢？如果不在超过图像的范围“摆”感受野，就没有神经元去检测出现在边界的模式，这样就会漏掉图像边界的地方，所以一般边界的地方也会考虑的。  超出范围就做**填充**。一般使用零填充。

第 2 个观察：同样的模式可能会出现在图像的不同区域

    同样的模式，可能会出现在图像的不同区域。因为感受野是盖满整个图像的，所以图像里面所有地方都在某个神经元的守备范围内。如果不同的守备范围都要有一个检测特征模式的神经元，参数量会太多了，因此需要做出相应的简化。

共享参数

    所谓参数共享就是两个神经元的权重完全是一样的。虽然两个神经元的参数是一模一样，但它们的输出不会永远都是一样的，因为它们的输入是不一样的，它们照顾的范围是不一样的。因为输入不一样的关系，所以就算是两个神经元共用参数，它们的输出也不会是一样的。每个感受野都只有一组参数而已，这些参数称为**滤波器**。

第 3 个观察：下采样不影响模式检测

    把一张比较大的图像做**下采样**，把图像偶数的列都拿掉，奇数的行都拿掉，图像变成为原来的 1/4，但是不会影响里面是什么东西。

汇聚

    根据第 3 个观察，**汇聚**被用到了图像识别中。汇聚没有参数，所以它不是一个层，它里面没有权重，它没有要学习的东西，汇聚比较像 Sigmoid、ReLU 等激活函数。因为它里面是没有要学习的参数的，它就是一个操作符，其行为都是固定好的，不需要根据数据学任何东西。每个滤波器都产生一组数字，要做汇聚的时候，把这些数字分组，可以 2 × 2 个一组，3 × 3、4 × 4 也可以，这个是我们自己决定的。

    做完卷积以后，往往后面还会搭配汇聚。汇聚就是把图像变小。做完卷积以后会得到一张图像，这张图像里面有很多的通道。做完汇聚以后，这张图像的通道不变。

上图为最大汇聚

    一般在实践上，往往就是卷积跟汇聚交替使用，可能做几次卷积，做一次汇聚。比如两次卷积，一次汇聚。不过汇聚对于模型的性能可能会带来一点伤害。假设要检测的是非常微细的东西，随便做下采样，性能可能会稍微差一点。

卷积神经网络的应用：下围棋

    网络的输入是一个向量，棋盘上有 19 × 19 个位置，可以把一个棋盘表示成一个 19 × 19 维的向量。在这个向量里面，如果某个位置有一个黑子，这个位置就填1，如果有白子，就填 -1，如果没有子，就填 0。不一定要黑子是 1，白子是 -1，没有子就是0，这只是一个可能的表示方式。通过把棋盘表示成向量，网络就可以知道棋盘上的盘势。把这个向量输到一个网络里面，下围棋就可以看成一个分类的问题，通过网络去预测下一步应该落子的最佳位置，所以下围棋就是一个有 19 × 19 个类别的分类问题，网络会输出 19 × 19个类别中的最好类别，据此选择下一步落子的位置。这个问题可以用一个全连接网络来解决，但用卷积神经网络的效果更好。