【C++】 排序算法合集 && 单元测试

排序算法是《数据结构与算法》中最基本的算法之一。

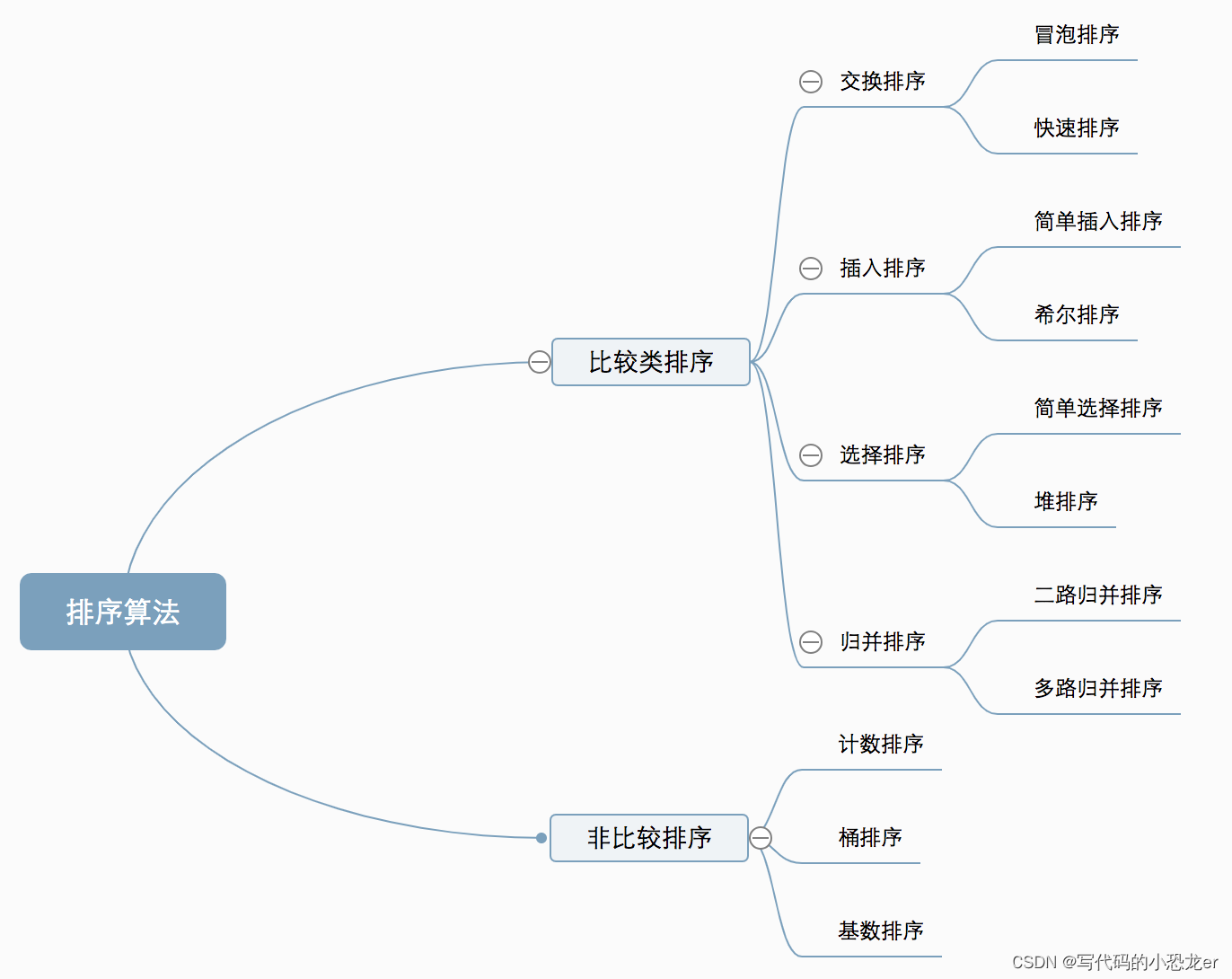
十种常见排序算法可以分为两大类：

• 比较类排序：通过比较来决定元素间的相对次序，时间复杂度为 O(nlogn)～O(n²)。
• 非比较类排序：不通过比较来决定元素间的相对次序，其时间复杂度可以突破 O(nlogn)，以线性时间运行。

【十大经典排序算法分类】

​

【十大经典排序算法的复杂度分析】

​

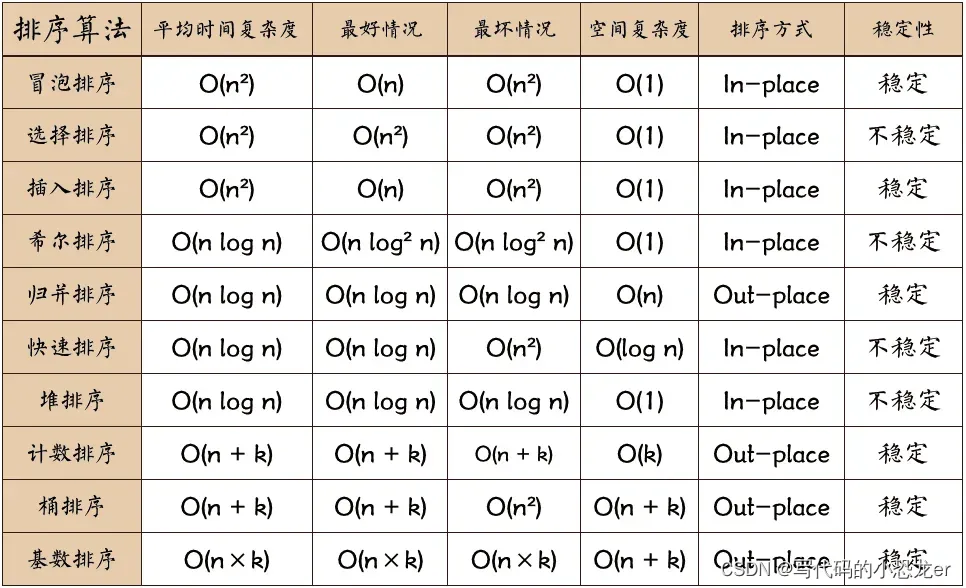
名词解释：

• 时间/空间复杂度：描述一个算法执行时间/占用空间与数据规模的增长关系。
• n：待排序列的个数。
• k：“桶”的个数（上面的三种非比较类排序都是基于“桶”的思想实现的）。
• In-place：原地算法，指的是占用常量内存，不占用额外内存。即空间复杂度为 O(1) 。
• Out-place：非原地算法，占用额外内存。
• 稳定性：假设待排序列中两元素相等，排序前后这两个相等元素的相对位置不变，则认为是稳定的。

一、排序算法代码合集 & 测试用例

    对前面分享的十种排序算法做单元测试。

1.1、博客地址

• 冒泡排序 & 选择排序：【C++】十大排序算法之 冒泡排序 & 选择排序-CSDN博客
• 插入排序 & 希尔排序：【C++】十大排序算法之 插入排序 & 希尔排序-CSDN博客
• 归并排序 & 快速排序：【C++】十大排序算法之 归并排序 & 快速排序-CSDN博客
• 堆排序 & 计数排序：【C++】十大排序算法之 堆排序 & 计数排序-CSDN博客
• 桶排序 & 基数排序：【C++】十大排序算法之 桶排序 & 基数排序-CSDN博客

1.2、 C++排序算法代码合集

/**
* @version Copyright (c) 2024 NCDC, Servo。 Unpublished - All rights reserved
* @file SortAlgorithm.hpp
* @brief 排序算法合集
* @autor 写代码的小恐龙er
* @date 2024/03/07
*/
// =================================================================
// ==========================十大排序算法===========================
// =================================================================
// 
// 
// 【冒泡排序】 -- 时间复杂度 O(n2) , 空间复杂度 O(1)
void BubbleSort(int arr[], int n) 
{
    // 设定一个交换标志 以提前结束排序
    bool isChange = false;

    // 最多做n - 1趟排序
    // 外循环为 趟数 
    for (int i = 0; i < n - 1; i++) {
        isChange = false;
        // 内循环为 针对后面的序列做冒泡排序
        for (int j = 0; j < n - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
                // 对交换标志位置位
                isChange = true;
            }
        }
        // 如果某一趟的排序未发生交换 则说明已经排序完成 无需后续排序
        if (!isChange) return;
    }
}

// 【选择排序】 -- 时间复杂度 O(n2) , 空间复杂度 O(1)
void SelectSort(int* arr, int n)
{
    // 存放最小元素的下标
    int minIndex = 0;
    // 存放每一次循环的起始位置的原始值（因为起始位置需要被最小元素替换）
    int temp = 0;

    // 排序 n - 1 次
    for (int i = 0; i < n - 1; i++) {
        minIndex = i;
        for (int j = i + 1; j < n; j++) {
            if (arr[j] < arr[minIndex]) minIndex = j;
        }

        // 将每一轮的最小值放置在循环起点
        if (minIndex != i) {
            temp = arr[minIndex];
            arr[minIndex] = arr[i];
            arr[i] = temp;
        }
    }
}

// 【插入排序】 -- 时间复杂度 O(n2) , 空间复杂度 O(1)
void InsertSort(int arr[], int n)
{
    int i = 0;
    int j = 0;
    int temp = 0;

    for (i = 1; i < n; i++) {
        temp = arr[i];

        //挪出位置
        for (j = i; j > 0 && arr[j - 1] > temp; j--) {
            arr[j] = arr[j - 1];
        }

        // 插入
        arr[j] = temp;

    }
}

// 【希尔排序】 -- 时间复杂度 O(n * logn) , 空间复杂度 O(1)
void ShellSort(int* arr, int size)
{
    int i, j, tmp, increment;
    // 选择一个增量序列 t1，t2，…，tk，其中 ti>tj，tk=1；
    // 按增量序列个数 k，对序列进行 k 趟排序；
    for (increment = size / 2; increment > 0; increment /= 2) {
        // 每趟排序，根据对应的增量 ti，将待排序列分割成若干长度为 m 的子序列，分别对各子表进行直接插入排序。 
        // 仅增量因子为 1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。
        for (i = increment; i < size; i++){
            tmp = arr[i];
            // 直接插入排序
            for (j = i - increment; j >= 0 && tmp < arr[j]; j -= increment) {
                arr[j + increment] = arr[j];
            }
            // 插入
            arr[j + increment] = tmp;
        }
    }
}

// 【归并排序】 -- 时间复杂度 O(n * logn) , 空间复杂度 O(n)
// 【分治法】&【递归法】
void Merge(int arr[], int l, int m, int r)
{
    // 将arr数组左右两个 有序序列合并在一起；
    int size = r - l + 1;
    vector<int> newArr(size, 0);

    // k代表新数组的下标
    int i = l, j = m + 1, k = 0;

    while (i <= m && j <= r) newArr[k++] = arr[i] <= arr[j] ? arr[i++] : arr[j++];
    while (i <= m) newArr[k++] = arr[i++];
    while (j <= r) newArr[k++] = arr[j++];

    // 重新赋值
    k = 0;
    for (i = l; i <= r; i++) {
        arr[i] = newArr[k++];
    }
}
// 递归
void MergeSort(int arr[], int l, int r)
{
    // 终止条件
    if (l >= r) return;

    // 中间节点
    int m = (l + r) / 2;
    // 分别递归进行子序列排列
    MergeSort(arr, l, m);
    MergeSort(arr, m + 1, r);
    // 最后将两个子序列合并在一块
    Merge(arr, l, m, r);

}

// 【快速排序】 -- 时间复杂度 O(n * logn) , 空间复杂度 O(logn) 
// 【分治法】&【递归法】
void QuickSort(int arr[], int begin, int end)
{
    // 终止条件
    if (begin > end) return;

    //基准数
    int pivot = arr[begin];
    int i = begin;
    int j = end;

    while (i != j) {
        // 从右向左 找比基准数小的数
        while (arr[j] >= pivot && i < j) j--;
        // 再从左向右找 比基准数 大的数
        while (arr[i] <= pivot && i < j) i++;
        if (i < j) {
            // 交换两个数在数组中的位置
            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
        }
    }

    // 最终将基准数归位 -- 将基准数 放置在 中间
    arr[begin] = arr[i];
    arr[i] = pivot;

    // 递归左右两侧的序列
    QuickSort(arr, begin, i - 1);
    QuickSort(arr, i + 1, end);

}

// 【堆排序】 -- 时间复杂度 O(n * logn) , 空间复杂度 O(1)
//void Swap(int arr[], int i, int j) {
//    int temp = arr[i];
//    arr[i] = arr[j];
//    arr[j] = temp;
//}
//void Heapify(int tree[], int n, int i) {
//    // n 表示序列长度，i 表示父节点下标
//    if (i >= n) return;
//    // 左侧子节点下标
//    int left = 2 * i + 1;
//    // 右侧子节点下标
//    int right = 2 * i + 2;
//    int max = i;
//    if (left < n && tree[left] > tree[max]) max = left;
//    if (right < n && tree[right] > tree[max]) max = right;
//    if (max != i) {
//        Swap(tree, max, i);
//        Heapify(tree, n, max);
//    }
//}
//void BuildHeap(int tree[], int n) {
//    // 树最后一个节点的下标
//    int last_node = n - 1;
//    // 最后一个节点对应的父节点下标
//    int parent = (last_node - 1) / 2;
//    int i;
//    for (i = parent; i >= 0; i--) {
//        Heapify(tree, n, i);
//    }
//}
//void HeapSort(int tree[], int n) 
//{
//    // 第一次建立大顶堆，从后向前依次调整
//    BuildHeap(tree, n);
//    // 每次将根和待排序的最后一次交换，然后再调整
//    int i;
//    for (i = n - 1; i >= 0; i--) {
//        // 将堆顶元素与最后一个元素交换
//        Swap(tree, i, 0);
//        // 调整成大顶堆
//        Heapify(tree, i, 0);
//    }
//}

// 【堆排序】 -- 时间复杂度 O(n * logn) , 空间复杂度 O(1)
void HeapAdjust(int* arr, int start, int end)
{
    int tmp = arr[start];
    for (int i = 2 * start + 1; i <= end; i = i * 2 + 1)
    {
        //有右孩子并且左孩子小于右孩子
        if (i < end && arr[i] < arr[i + 1]){
            i++;
        }//i一定是左右孩子的最大值
        if (arr[i] > tmp)
        {
            arr[start] = arr[i];
            start = i;
        }
        else break;
    }
    arr[start] = tmp;
}
void HeapSort(int* arr, int len)
{
    //第一次建立大根堆，从后往前依次调整
    for (int i = (len - 1 - 1) / 2; i >= 0; i--){
        HeapAdjust(arr, i, len - 1);
    }
    //每次将根和待排序的最后一次交换，然后在调整
    int tmp;
    for (int i = 0; i < len - 1; i++){
        tmp = arr[0];
        arr[0] = arr[len - 1 - i];
        arr[len - 1 - i] = tmp;
        HeapAdjust(arr, 0, len - 1 - i - 1);
    }
}

// 【计数排序】 -- 时间复杂度 O(n + k) , 空间复杂度 O(k)
void CountingSort(int arr[], int n) 
{
    if (arr == NULL) return;
    // 寻找最值元素
    int max = arr[0], min = arr[0];
    int i;
    for (i = 1; i < n; i++) {
        if (max < arr[i]) max = arr[i];
        if (min > arr[i]) min = arr[i];
    }
    int r = max - min + 1;
    // 定义辅助空间并初始化
    vector<int> C(r, 0);

    // 统计每个元素出现的次数
    for (i = 0; i < n; i++) C[arr[i] - min]++;

    i = 0;
    for (int j = 0; j < r; j++) {
        while (C[j]--) {
            arr[i++] = j + min;
        }
    }
}
// 【计数排序- 重载】 -- 时间复杂度 O(n + k) , 空间复杂度 O(k)
void CountingSort(vector<int> arr, int n)
{
    if (n == 0) return;
    // 寻找最值元素
    int max = arr[0], min = arr[0];
    int i;
    for (i = 1; i < n; i++) {
        if (max < arr[i]) max = arr[i];
        if (min > arr[i]) min = arr[i];
    }
    int r = max - min + 1;
    // 定义辅助空间并初始化
    vector<int> C(r, 0);

    // 统计每个元素出现的次数
    for (i = 0; i < n; i++) C[arr[i] - min]++;

    i = 0;
    for (int j = 0; j < r; j++) {
        while (C[j]--) {
            arr[i++] = j + min;
        }
    }
}

// 【桶排序】 -- 时间复杂度 O(n + k) , 空间复杂度 O(n + k)
void BucketSort(int arr[], int n, int r) 
{
    if (arr == NULL || r < 1) return;

    // 根据最大/最小元素和桶数量，计算出每个桶对应的元素范围
    int max = arr[0], min = arr[0];
    int i, j;
    for (i = 1; i < n; i++) {
        if (max < arr[i]) max = arr[i];
        if (min > arr[i]) min = arr[i];
    }
    int range = (max - min + 1) / r++;

    // 建立桶对应的二维数组，一个桶里最多可能出现 n 个元素
    vector<vector <int>> buckets(r, vector <int>(n, 0));
    vector <int> counts(n, 0);

    for (i = 0; i < n; i++) {
        int k = (arr[i] - min) / range;
        buckets[k][counts[k]++] = arr[i];
    }

    int index = 0;
    for (i = 0; i < r; i++) {
        // 分别对每个非空桶内数据进行排序，比如计数排序
        if (counts[i] == 0) continue;
        sort(buckets[i].begin(), buckets[i].begin() + counts[i]);
        // CountingSort(buckets[i], counts[i]);
        // 拼接非空的桶内数据，得到最终的结果
        for (j = 0; j < counts[i]; j++) {
            arr[index++] = buckets[i][j];
        }
    }
}

// 基数
#define RADIX 10

// 【基数排序】 -- 时间复杂度 O(n * k) , 空间复杂度 O(n + k)
void RadixSort(int arr[], int n) 
{
    // 获取最大值和最小值
    int max = arr[0], min = arr[0];
    int i, j, l;
    for (i = 1; i < n; i++) {
        if (max < arr[i]) max = arr[i];
        if (min > arr[i]) min = arr[i];
    }
    // 假如序列中有负数，所有数加上一个常数，使序列中所有值变成正数
    if (min < 0) {
        for (i = 0; i < n; i++) arr[i] -= min;
        max -= min;
    }
    // 获取最大值位数
    int d = 0;
    while (max > 0) {
        max /= 10;
        d++;
    }
    vector<vector <int>> queue(RADIX, vector <int>(n, 0));
    int count[RADIX] = { 0 };
    for (i = 0; i < d; i++) {
        // 分配数据
        for (j = 0; j < n; j++) {
            // 依次 从 个位 到最高位 取出 数值
            int key = arr[j] % (int)pow(RADIX, i + 1) / (int)pow(RADIX, i);
            // 放置到 对应 位数的数组中   count[key]++ 是为了记录 位数相同的  值 共有多少个
            queue[key][count[key]++] = arr[j];
        }
        // 收集数据
        int c = 0;
        // 依次将各个基数中的数据排列起来
        for (j = 0; j < RADIX; j++) {
            for (l = 0; l < count[j]; l++) {
                arr[c++] = queue[j][l];
                queue[j][l] = 0;
            }
            count[j] = 0;
        }
    }
    // 假如序列中有负数，收集排序结果时再减去前面加上的常数
    if (min < 0) {
        for (i = 0; i < n; i++) arr[i] += min;
    }
}

1.3 、C++测试代码

/**
* @version Copyright (c) 2024 NCDC, Servo。 Unpublished - All rights reserved
* @file SortTest.hpp
* @brief 排序算法测试用例
* @autor 写代码的小恐龙er
* @date 2024/03/07
*/

// 头文件
#include <iostream>
#include <fstream>
#include <vector>
#include <algorithm>
#include <memory>

void SortTest() 
{
    // 数组中的元素个数
    int n = 10;
    // 起始下标
    int begin = 0;
    // 终止下标
    int end = 9;
    int l = 0;
    int r = 9;

    // ============ 冒泡排序 =============
    int arr1[10] = {2,5,8,4,0,6,1,3,7,9};
    BubbleSort(arr1, n);
    printf("冒泡排序后为:");
    for (int i = 0; i < sizeof(arr1) / sizeof(arr1[0]); i++)
    {
        printf("%d ", arr1[i]);
    }
    std::cout << endl;

    // ============选择排序 =============
    int arr2[10] = { 2,5,8,4,0,6,1,3,7,9 };
    SelectSort(arr2, n);
    printf("选择排序后为:");
    for (int i = 0; i < sizeof(arr2) / sizeof(arr2[0]); i++)
    {
        printf("%d ", arr2[i]);
    }
    std::cout << endl;

    // ============ 插入排序 =============
    int arr3[10] = { 2,5,8,4,0,6,1,3,7,9 };
    InsertSort(arr3, n);
    printf("插入排序后为:");
    for (int i = 0; i < sizeof(arr3) / sizeof(arr3[0]); i++)
    {
        printf("%d ", arr3[i]);
    }
    std::cout << endl;

    // ============ 希尔排序 =============
    int arr4[10] = { 2,5,8,4,0,6,1,3,7,9 };
    ShellSort(arr4, n);
    printf("希尔排序后为:");
    for (int i = 0; i < sizeof(arr4) / sizeof(arr4[0]); i++)
    {
        printf("%d ", arr4[i]);
    }
    std::cout << endl;

    // ============ 归并排序 =============
    int arr5[10] = { 2,5,8,4,0,6,1,3,7,9 };
    MergeSort(arr5, l, r);
    printf("归并排序后为:");
    for (int i = 0; i < sizeof(arr5) / sizeof(arr5[0]); i++)
    {
        printf("%d ", arr5[i]);
    }
    std::cout << endl;

    // ============ 快速排序 =============
    int arr6[10] = { 2,5,8,4,0,6,1,3,7,9 };
    QuickSort(arr6, begin, end);
    printf("快速排序后为:");
    for (int i = 0; i < sizeof(arr6) / sizeof(arr6[0]); i++)
    {
        printf("%d ", arr6[i]);
    }
    std::cout << endl;

    // ============ 堆排序 =============
    int arr7[10] = { 2,5,8,4,0,6,1,3,7,9 };
    HeapSort(arr7, n);
    printf("堆排序后为  :");
    for (int i = 0; i < sizeof(arr7) / sizeof(arr7[0]); i++)
    {
        printf("%d ", arr7[i]);
    }
    std::cout << endl;

    // ============ 计数排序 =============
    int arr8[10] = { 2,5,8,4,0,6,1,3,7,9 };
    CountingSort(arr8, n);
    printf("计数排序后为:");
    for (int i = 0; i < sizeof(arr8) / sizeof(arr8[0]); i++)
    {
        printf("%d ", arr8[i]);
    }
    std::cout << endl;

    // ============ 桶排序 =============
    int arr9[10] = { 2,5,8,4,0,6,1,3,7,9 };
    BucketSort(arr9, n, 3);
    printf("桶排序后为  :");
    for (int i = 0; i < sizeof(arr9) / sizeof(arr9[0]); i++)
    {
        printf("%d ", arr9[i]);
    }
    std::cout << endl;

    // ============ 基数排序 =============
    int arr10[10] = { 2,5,8,4,0,6,1,3,7,9 };
    RadixSort(arr10, n);
    printf("基数排序后为:");
    for (int i = 0; i < sizeof(arr10) / sizeof(arr10[0]); i++)
    {
        printf("%d ", arr10[i]);
    }
    std::cout << endl;
}

using namespace std;

int main()
{
    cout << "-----------------------------------------------" << endl;
    cout << "单元测试用例 ： " << endl;
    cout << "-----------------------------------------------" << endl;

    // 排序算法的单元测试
    SortTest();
    cout << "-----------------------------------------------" << endl;

    system("pause");
    return 0;
}

1.4 、输出结果

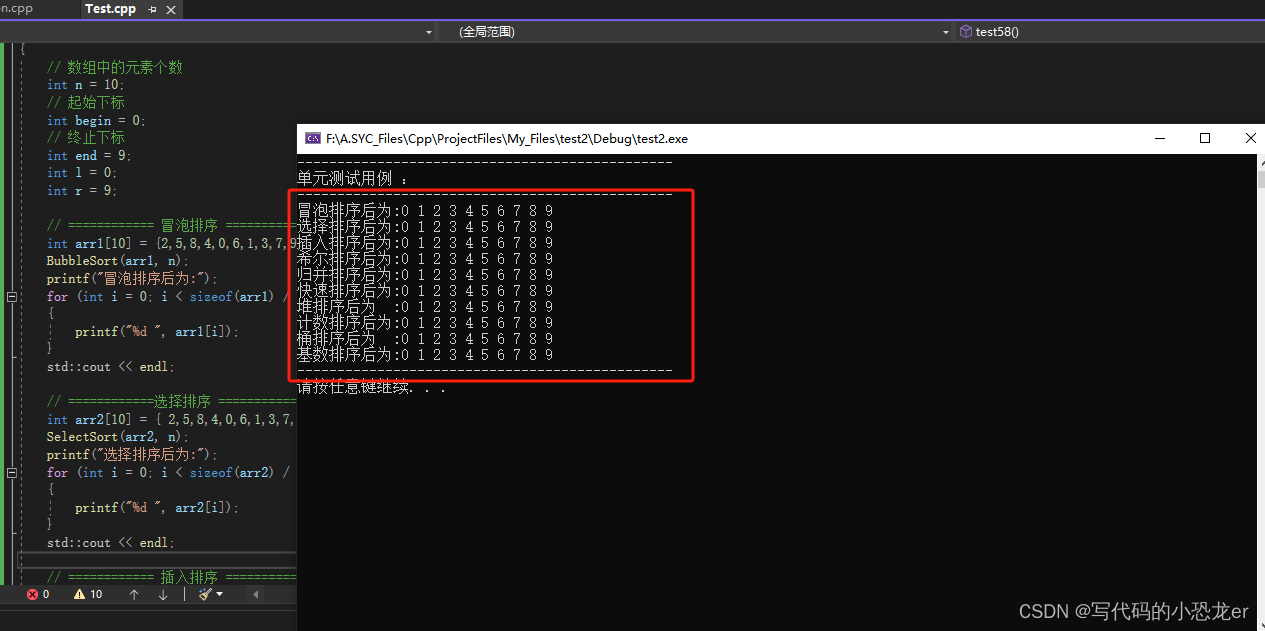
-- 排序算法结束。