人工智能/机器学习基础知识——欠采样&过采样（UnderSampling & OverSampling）

UnderSampling & OverSampling

博客园

博客园

欠采样 & 过采样

UnderSampling

欠采样

EasyEnsemble

Bagging

• 算法流程- 将多类样本随机划分成n个子集，每个子集的数量等于少数类样本的数量- 再将每个子集与其余少数类样本结合起来分别训练一个模型- 最后将n个模型集成

Balance Cascade

Boosting

• 算法流程- 第n轮训练：从多数样本中采样一部分样本与少数类样本结合起来训练一个模型 M n M_n Mn​- 第n + 1轮训练：上一轮训练完成后，将能被 M n M_n Mn​正确分类的多数样本剔除，再从现在的多数样本中采样一部分与少数类样本结合起来训练下一个模型 M n + 1 M_{n+1} Mn+1​- 最后将训练所得各个阶段的模型进行集成（加权平均）

NearMiss

• NearMiss-1- 选择到最近的K个少数类样本平均距离最近的多数类样本
• NearMiss-2- 选择到最远的K个少数类样本平均距离最近的多数类样本
• NearMiss-3- 对于每个少数类样本选择K个最近的多数类样本，目的是保证每个少数类样本都被多数类样本包围

Tomek Link

Tomek Link：表示不同类别之间距离最近的一对样本，即这两个样本互为最近邻且属于不同类别

• 如果两个样本形成了一个Tomek Link，可以认为要么其中一个是噪声，要么两个样本都在边界附近
• 通过移除Tomek Link就能清洗掉类间重叠样本，使得互为最近邻的样本皆属同一类别，从而能更好地进行分类

Edited Nearest Neighbours（ENN）

对于属于多数类的一个样本，如果其K个近邻点有超过一半都不属于多数类，则这个样本会被剔除

OverSampling

过采样

Synthetic Minority Oversampling Technique（SMOTE）

对少数类样本进行分析并根据少数类样本人工合成新样本添加到数据集中

SMOTE-Regular

• 算法流程> 假设数据为二维平面上的点集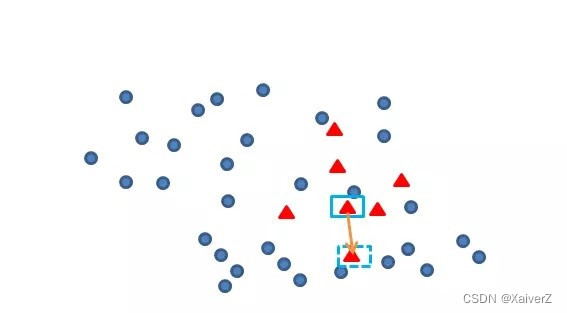- 对于每一个少数类样本 x x x- 找出该样本的k个近邻（k为超参数，由于数据为二维平面点集，故此用欧氏距离）- 对于k个近邻，选取其中m个样本，对每一个样本 x ′ x' x′，以如下方式构造新样本（m为超参数） x n e w = x + r a n d ( 0 , 1 ) ⋅ x ′ x_{new} = x + rand(0, 1) · x' xnew​=x+rand(0,1)⋅x′

SMOTE-Borderline

Paper : Borderline-SMOTE: A New Over-Sampling Method in Imbalanced Data Sets Learning

• 算法流程> 核心算法和SMOTE-Regular一致，区别在于SMOTE-Borderline只对边界样本生成新样本（边界样本即k近邻半数以上都为多数类样本的少数类样本）

ADASYN

核心算法还是SMOTE，ADASYN先计算出需要合成的样本总量再调用SMOTE

• 算法流程- 计算需要合成的样本总量 G = （ S m a x − S m i n ） ⋅ β G = （S_{max} - S_{min}）· β G=（Smax​−Smin​）⋅β其中 S m a x S_{max} Smax​为多数类样本数量， S m i n S_{min} Smin​为少数类样本数量， β β β为超参数。G为总共需合成的少数类样本数量。- 对于每个少数类样本 x i x_i xi​，找出其k近邻，并计算 Γ i = Δ i / K Z Γ_i = \frac{Δ_i / K}{Z} Γi​=ZΔi​/K​其中 Δ i Δ_i Δi​为k近邻个点中多数类样本的数量，Z为规范化因子以确保Γ构成一个分布。- 最后对每个少类样本 x i x_i xi​计算需要合成的样本数量g_i，再用SMOTE算法合成新样本 g i = Γ i ⋅ G g_i = Γ_i · G gi​=Γi​⋅G

过采样（OverSampling）与欠采样（UnderSampling）结合

由于过采样后容易产生很多与周围样本“相似度”过高的重叠样本，增大模型分类难度，而欠采样可以去除这些重叠度过大的样本。故可将二者结合起来，先进行过采样再进行欠采样，如SMOTE + ENN 或 SMOTE + Tomek