手把手教你实现AVL树、平衡二叉树

今天，小编带大家一起来学习平衡二叉树（AVL树）吧。以下就简称AVL树了。

想必能点开这篇博客的朋友都是极度深爱计算机的，那今天就让我们一起揭开AVL树的神秘面纱吧！

目录

一.基本概念

AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis。

AVL树是搜索二叉树的一种特殊形式。本质上还是一棵搜索二叉树，遵循着左小右大的原则。

但与普通搜索二叉树不同的是，它每个节点的左右子树高度差都不超过1。

为什么要这么设计呢？ 我们举个例子便理解了。

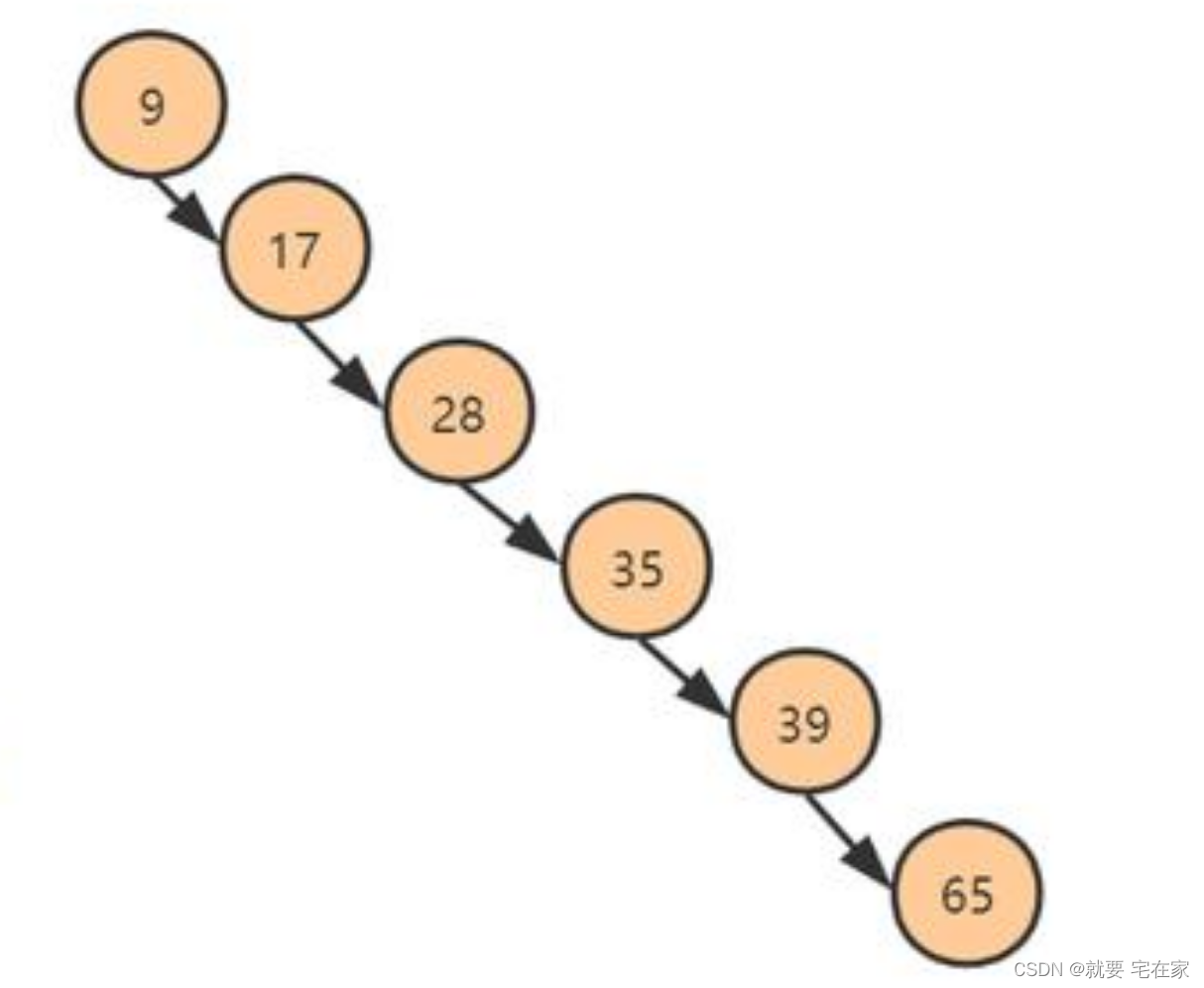
这里要是进行查找65这个数的时候，我们需要一遍遍的递归，直到这颗树的树底。但这样一棵树递归次数太多，高度低还好，如果一棵树太高，就有可能造成递归次数太多，引起栈溢出。

就算不会引起栈溢出，这种树有多高就递归几次的方式，效率也是极低的。

所以我们需要在保持左小右大的前提下，让树的高度尽可能的低，达到一种节点的左右子树高度差不大于1的效果，即是AVL树。

那以上图为例，AVL树就是这样：

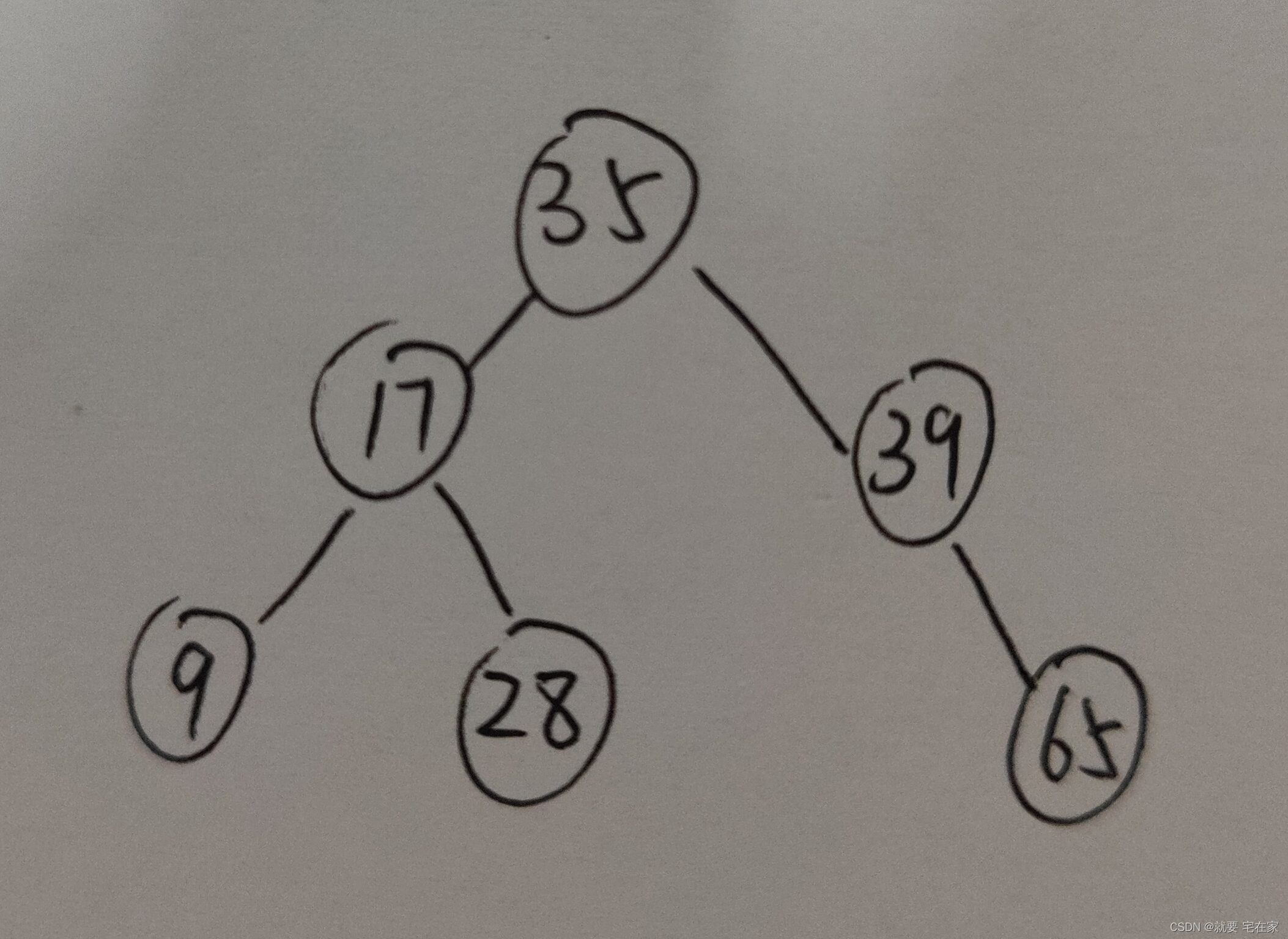
这里，我们就能看出来了，要是找到65这个数子，我们只需要递归2次，而原树则需要5次。

所以，AVL树可以理解为是搜索二叉树的优化版本。

二.实现原理

我们首先要知道节点怎么左旋转和右旋转。

（一）右旋转

以上图为例，将L右旋转的话，就是L的右子树变成A，L原来的右子树变成A的左子树即可。

（二）左旋转

与右旋转相反，将L左旋转，就是L左子树变成A，L原来的左子树变成A的右子树。

（三）整体思路

既然要实现AVL树，那么我们就需要用到几个参数。

1.struct AVLTree ，这是AVL树的结构体，结构体里除了装数据的val和连接左右子树的指针外，还应该有一个用来判断该节点左右子树高度差的参数bf。bf参数设为int类型，-1代表左子树高，0代表树一般高，1代表右子树高。同时也应注意：结构体的每个节点都应该是指针类型的，所以在一开始定义结构体变量的时候，就要定义一个指针类型的结构体。

2.bool judge_hight，这是一个bool类型的参数，用来判断这一次插入节点后，该节点的子树是否有长高的。judge_hight 初始化为true即可，因为第一次插入数据，树一定会长高。

下面，我们就可以创建AVL树了！

函数声明：void AVLTree_Insert(AVLTree* at, bool judge_hight);

AVL树元素的插入方式与搜索二叉树大体类似，但有些许不同：

假设我们现在有一个数据，按照左小右大的规则插入搜索二叉树后，当找到一个位置插入数据后，我们需要判断树是否长高了，这里就需要分为两大类了：

插入左子树和插入右子树。

（四）数据插入左子树

如果数据是插入了节点a的左子树导致长高，那么我们就需要判断a的左右子树高度差（bf）这里分为三种情况：

bf = 0 左右子树平衡，将bf改为1即可。

bf = -1 右边高， 加入左节点，树就平衡了，bf改为0，judge_hight置为false。

bf = 1 左边高，需要调用函数来判断该节点a是否还平衡，之后judge_hight置为false。设调用的函数为：void Treebalance_left(AVLTree* at)。在这个函数里，我们就需要继续判断是插入了l的左节点还是右节点。

①插入左子树左子节点

插入左子节点的含义是：节点插入a的左子树后，使a不再平衡，原因是a的左子树的左边变高。

以下三种均为插入左子节点的情况，这三种看似不同，其实一致，均是l的左边高。

图上看已经很清楚了， a的已经不平衡了，我们就需要进行右旋转a的左子节点来使a平衡。

相当于直接把l提到a的位置。

旋转后结果如图：

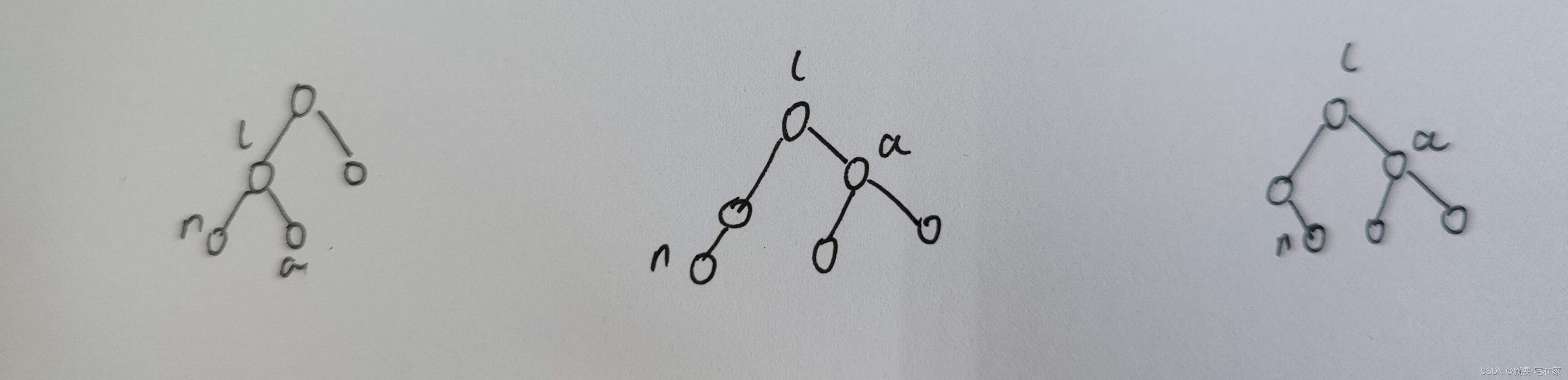
这里可以看出，a的bf改为0，l的bf改为0。

②插入左子树右子节点

与插入左子节点相反，插入右子节点是指：节点a不平衡是因为左边高，而a左边高是因为a的左子节点的右边高。也就是在a的左子节点插入了右子树。

同理，以下三种均为插入右子节点的情况，即a不平衡，l的右边高。

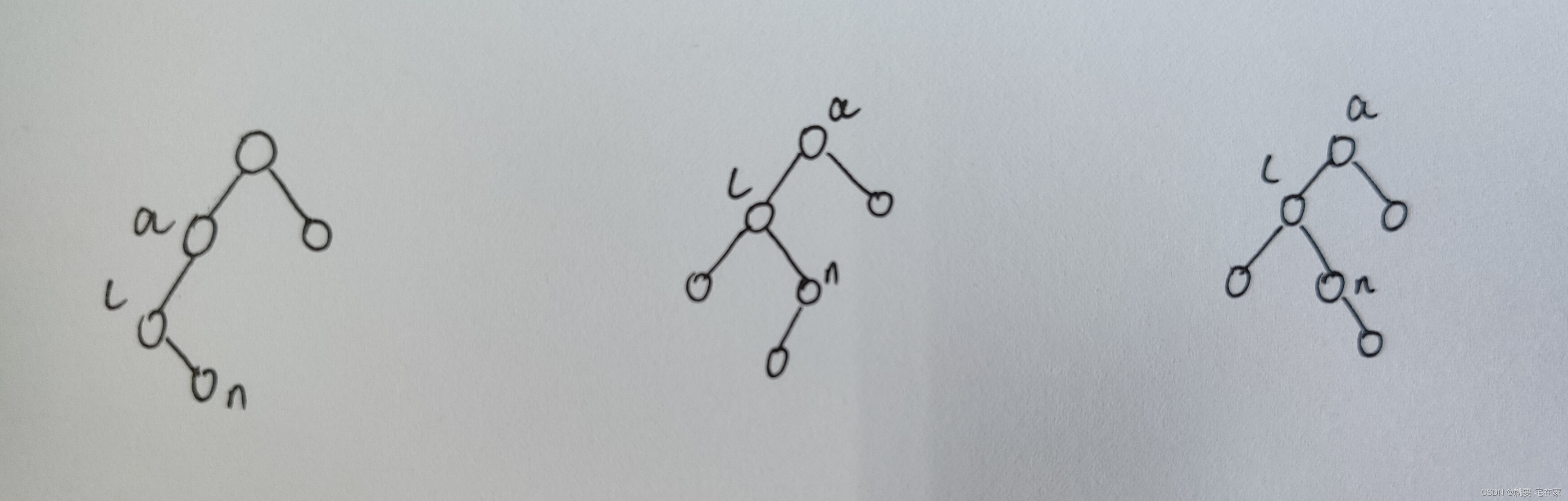
对于a而言，这种也是不平衡的情况，那么我们需要先对l进行左旋转，再对n进行右旋转。

这里值得注意的是：l左旋转后n右旋转，其实就是使n先转到l的位置，再转到a的位置。

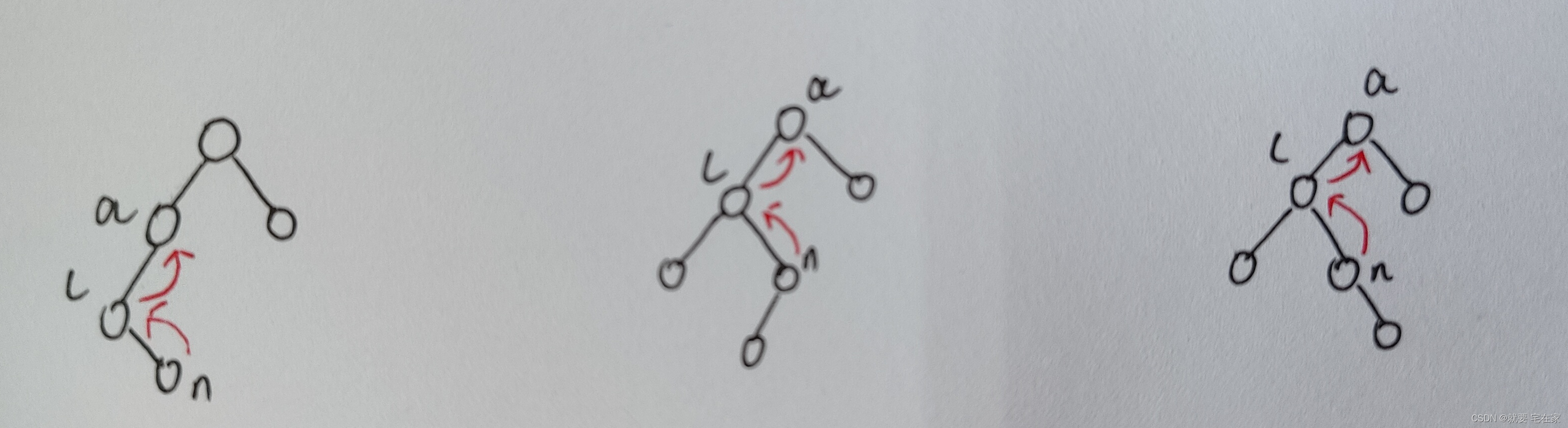
第一步：l左旋转（n转到l位置）

第二步：n右旋转（n转到a位置）

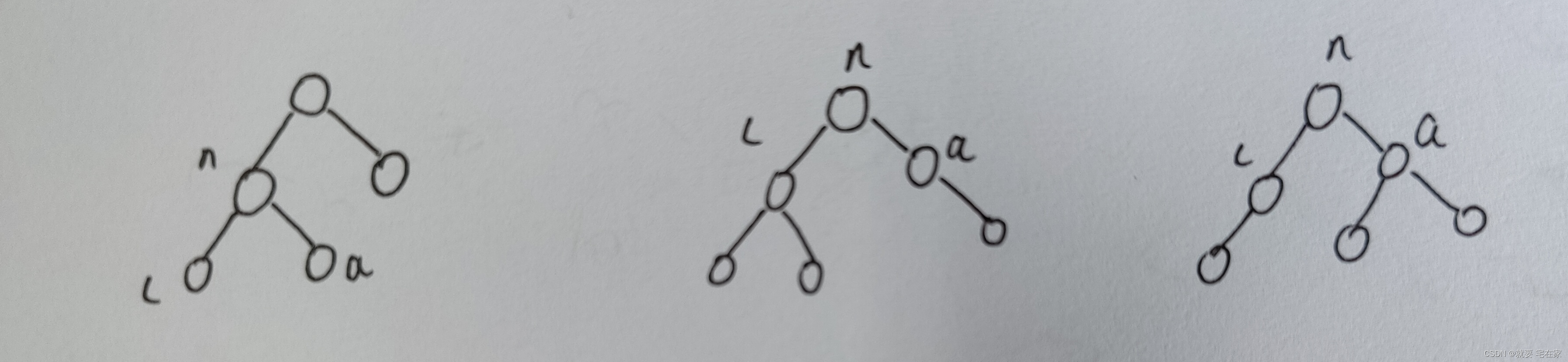
这里我们需要注意的是：此时a与l的bf值三棵树并不相同。为什么呢，因为一开始的时候三棵树n的左右子树高度并不相同。

下面给出n的bf值与a、l的bf值的规律：
第一棵第二棵第三棵n的BF值01-1a和l的BF值a=0 l=0a=-1 l=0a=0 l=1
我们需要注意的是，三棵树的旋转方式一样，但BF值不同，所以在代码里要先判断n的BF值再旋转。

（五）数据插入右子树

数据插入右子树，我们也需要判断此时节点的平衡情况，再做下一步打算。同样的，也是先判断插入数据前节点的bf值来判断，也分三种情况：

BF=0：插入右子树后BF=-1

BF=1：插入右子树后，节点平衡，BF=0，judge_hight置为false。

BF=-1：插入右子树后节点可能不平衡，需要调用函数判断一下。之后judge_hight置为false。

可以设调用的函数为void Treebalance_right(AVLTree* at);这个函数里，我们要传入该节点的右子树，判断数据是插入它的左子节点还是右子节点。

①插入右子树右子节点

以下三棵树均为插入右子节点的情况。三棵树平衡方式一样，均为l左旋转，使l转到a的位置。

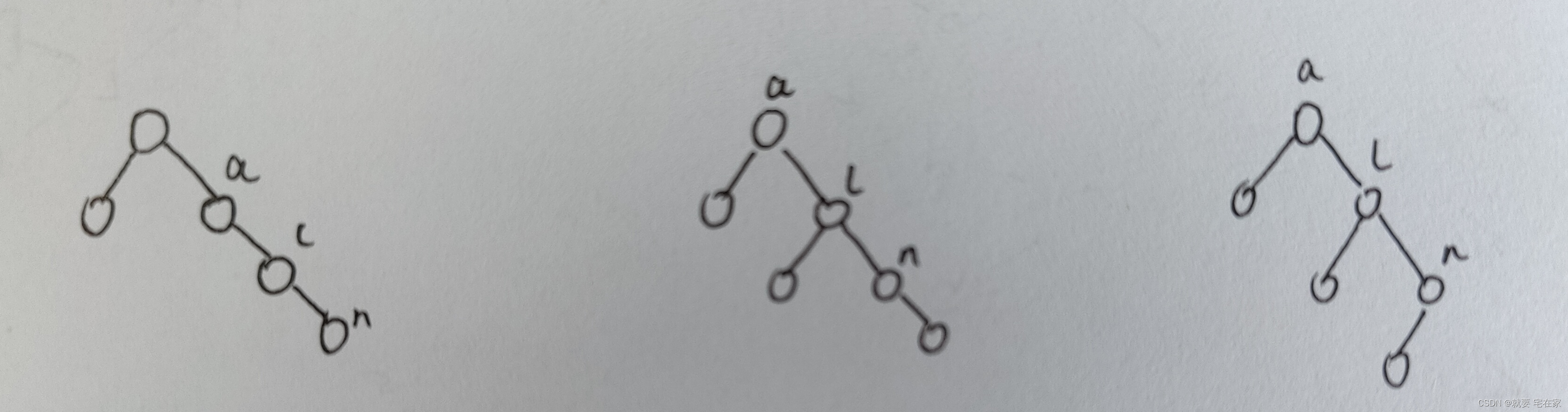
l左旋转后：

②插入右子树左子节点

以下三棵树均为插入左子节点的情况，旋转方式均为l右旋转后n左旋转，即n先跳到l位置后跳到a位置。

但是与插入左子树右子节点类似，要先判断n的BF值,写出相应的a与l旋转后的BF值再旋转。这里小编先给大家旋转完再判断BF值。（代码里一定要先判断！）

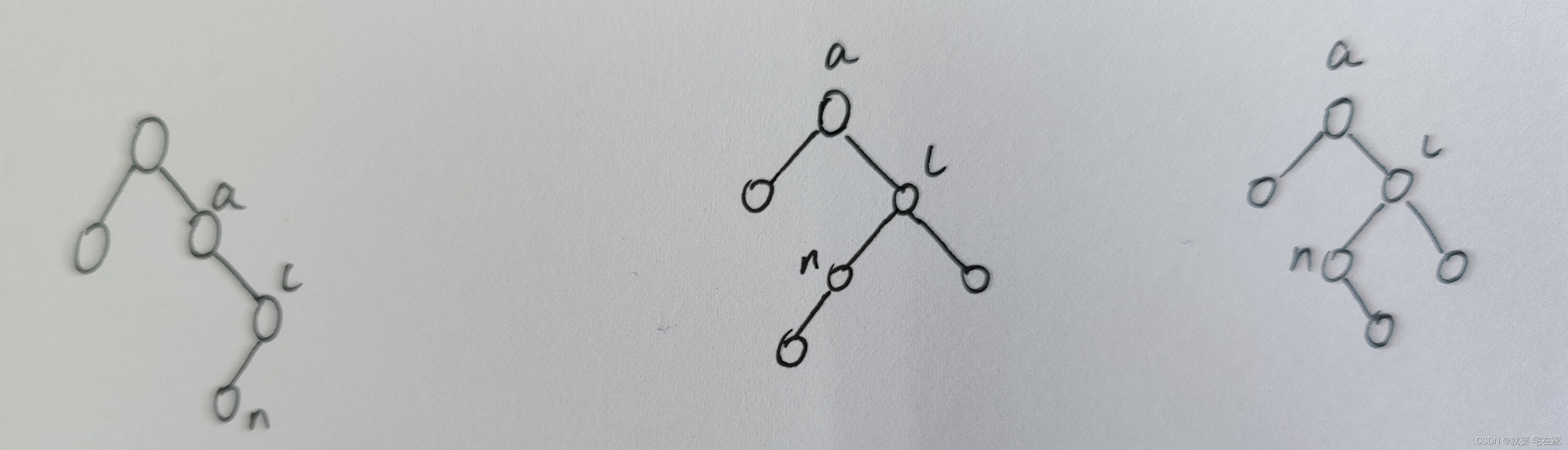
l右旋转（n跳到l的位置）

n左旋转（n跳到a的位置）

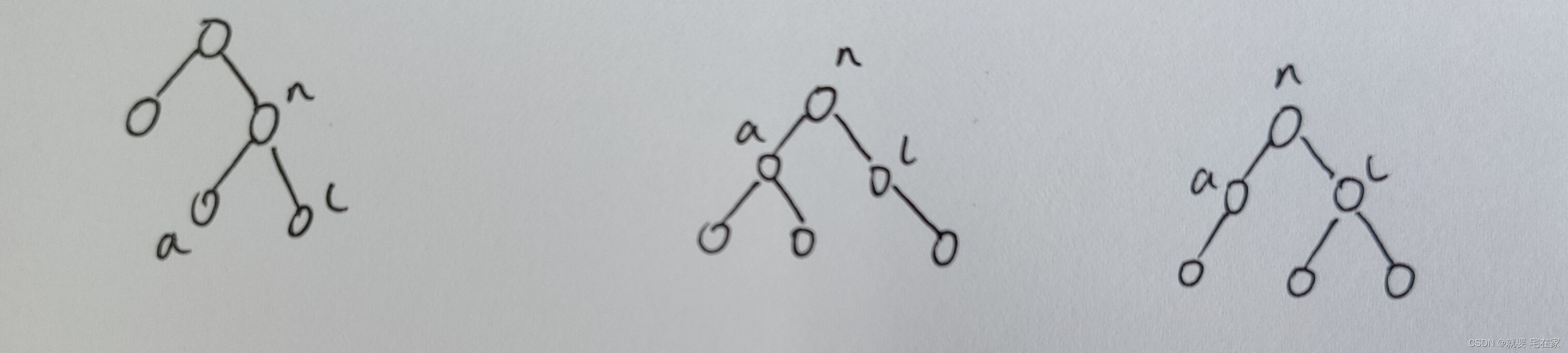
到这里,n的BF值与a、l的BF值的关系也就出来了。
n的BF值01 -1a的BF值001l的BF值0 -10

（六）思维导图

三.代码实现

#define LH 1//左树高
#define NH 0//一般高
#define RH -1//右树高
typedef int AVLTreetype;
typedef struct Tree
{
    AVLTreetype val;
    struct Tree* leftchild, * rightchild;
    int bf;//此节点子树的高度差
}*AVLTree, Tree;
void AVLTree_Insert(AVLTree& at, AVLTreetype n, bool& judge_hight);//插入AVL树
void AVLTreebalance_left(AVLTree& at);//判断左树是否平衡
void AVLTreebalance_right(AVLTree& at);//判断右树是否平衡
void L_Roll(AVLTree& at);//左旋
void R_Roll(AVLTree& at);//右旋
void AVLTree_Insert(AVLTree& at, AVLTreetype n, bool& judge_hight)//插入
{
    if (at == NULL)
    {
        AVLTreeinit(at, n);
        judge_hight = true;
        return;
    }
    else
    {
        if (n == at->val)
        {
            cout << "\nHave Insert：" << n << endl;
            judge_hight = false;
            return;
        }
        else if (n < at->val)
        {
            if (at->leftchild)
            {
                AVLTree_Insert(at->leftchild, n, judge_hight);//递归
            }
            else// at->leftchild == NULL
            {
                AVLTreeinit(at->leftchild, n);
                judge_hight = true;
            }
            if (judge_hight)
            {
                switch (at->bf)
                {
                case LH:
                    judge_hight = false;
                    AVLTreebalance_left(at);//判断是否平衡
                    break;
                case NH:
                    at->bf = LH;
                    break;
                case RH:
                    at->bf = NH;
                    judge_hight = false;
                    break;
                }
            }
        }
        else
        {
            if (at->rightchild)
            {
                AVLTree_Insert(at->rightchild, n, judge_hight);
            }
            else// at->rightchild == NULL
            {
                AVLTreeinit(at->rightchild, n);
                judge_hight = true;
            }
            if (judge_hight)
            {
                switch (at->bf)
                {
                case RH:
                    judge_hight = false;
                    AVLTreebalance_right(at);
                    break;
                case NH:
                    at->bf = RH;
                    break;
                case LH:
                    at->bf = NH;
                    judge_hight = false;
                    break;
                }
            }
        }
    }
}
void AVLTreebalance_left(AVLTree& at)
{
    AVLTree l = at->leftchild, lr = l->rightchild;
    switch (l->bf)
    {
    case LH：
        at->bf = l->bf = NH;
        R_Roll(at);
        break;
    case RH:
        switch (lr->bf)
        {
        case LH:
            at->bf = RH;
            l->bf = NH;
            break;
        case NH:
            at->bf = l->bf = NH;
            break;
        case RH:
            at->bf = NH;
            l->bf = LH;
            break;
        }
        L_Roll(at->leftchild);
        R_Roll(at);
        break;
    }
}
void AVLTreebalance_right(AVLTree& at)//判断树右边是否平衡
{
    AVLTree r = at->rightchild, rl = r->leftchild;
    switch (r->bf)
    {
    case RH:
        at->bf = r->bf = NH;/
        L_Roll(at);
        break;
    case LH:
        switch (rl->bf)
        {
        case LH:
            at->bf = NH;
            r->bf = RH;
            break;
        case NH:
            at->bf = r->bf = NH;
            break;
        case RH:
            at->bf = LH;
            r->bf = NH;
            break;
        }
        R_Roll(at->rightchild);
        L_Roll(at);
        break;
    }
}
void L_Roll(AVLTree& at)//左旋
{
    AVLTree r = at->rightchild;
    at->rightchild = r->leftchild;
    r->leftchild = at;
    at = r;
}
void R_Roll(AVLTree& at)//右旋
{
    AVLTree l = at->leftchild;
    at->leftchild = l->rightchild;
    l->rightchild = at;
    at = l;
}

小编呕心沥血之作，恳请点赞关注支持一下吧~😃 如有错误，敬请斧正