第 三 章 课 后 习 题
T 3.1
考虑文法
S
→
(
L
)
∣
a
L
→
L
,
S
∣
S
S \rightarrow (L)\space | \space a\\ L\rightarrow L, S \space | \space S
S→(L) ∣ aL→L,S ∣ S
**(a) 建立句子
(
a
,
(
a
,
a
)
)
(a,(a,a))
(a,(a,a)) 和
(
a
,
(
a
,
a
)
,
(
a
,
a
)
)
(a,(a,a),(a,a))
(a,(a,a),(a,a)) 的分析树。**
见下面两题。
(b) 为 (a) 的两个句子构造最左推导。
(
a
,
(
a
,
a
)
)
(a,(a,a))
(a,(a,a)) 最左推导的分析树(包括推导过程中的分析树):

(
a
,
(
a
,
a
)
,
(
a
,
a
)
)
(a,(a,a),(a,a))
(a,(a,a),(a,a)) 最左推导的分析树:
S
⇒
l
m
(
L
)
⇒
l
m
(
L
,
S
)
⇒
l
m
(
S
,
S
)
⇒
l
m
(
a
,
S
)
⇒
l
m
(
a
,
(
L
)
)
⇒
l
m
(
a
,
(
L
,
S
)
)
⇒
l
m
(
a
,
(
S
,
S
)
)
⇒
l
m
(
a
,
(
(
L
)
,
S
)
)
⇒
l
m
(
a
,
(
(
L
,
S
)
,
S
)
)
⇒
l
m
(
a
,
(
(
S
,
S
)
,
S
)
)
⇒
l
m
(
a
,
(
(
a
,
S
)
,
S
)
)
⇒
l
m
(
a
,
(
(
a
,
a
)
,
S
)
)
⇒
l
m
(
a
,
(
(
a
,
a
)
,
(
L
)
)
)
⇒
l
m
(
a
,
(
(
a
,
a
)
,
(
L
)
)
)
⇒
l
m
(
a
,
(
(
a
,
a
)
,
(
L
,
S
)
)
)
⇒
l
m
(
a
,
(
(
a
,
a
)
,
(
S
,
S
)
)
)
⇒
l
m
(
a
,
(
(
a
,
a
)
,
(
a
,
S
)
)
)
⇒
l
m
(
a
,
(
(
a
,
a
)
,
(
a
,
a
)
)
)
S\Rightarrow_{lm} (L)\Rightarrow_{lm} (L,S) \Rightarrow_{lm} (S,S) \Rightarrow_{lm} (a,S) \Rightarrow_{lm}(a,(L)) \Rightarrow_{lm} (a,(L,S)) \Rightarrow_{lm} (a,(S,S)) \Rightarrow_{lm} (a,((L),S))\\ \Rightarrow_{lm} (a,((L,S),S)) \Rightarrow_{lm} (a,((S,S),S))\Rightarrow_{lm} (a,((a,S),S)) \Rightarrow_{lm} (a,((a,a),S)) \Rightarrow_{lm} (a,((a,a),(L)))\\ \Rightarrow_{lm} (a,((a,a),(L))) \Rightarrow_{lm} (a,((a,a),(L,S)))\Rightarrow_{lm} (a,((a,a),(S,S))) \Rightarrow_{lm} (a,((a,a),(a,S))) \Rightarrow_{lm} (a,((a,a),(a,a)))
S⇒lm(L)⇒lm(L,S)⇒lm(S,S)⇒lm(a,S)⇒lm(a,(L))⇒lm(a,(L,S))⇒lm(a,(S,S))⇒lm(a,((L),S))⇒lm(a,((L,S),S))⇒lm(a,((S,S),S))⇒lm(a,((a,S),S))⇒lm(a,((a,a),S))⇒lm(a,((a,a),(L)))⇒lm(a,((a,a),(L)))⇒lm(a,((a,a),(L,S)))⇒lm(a,((a,a),(S,S)))⇒lm(a,((a,a),(a,S)))⇒lm(a,((a,a),(a,a)))
(c) 为 (a) 的两个句子构造最右推导。
(
a
,
(
a
,
a
)
)
(a,(a,a))
(a,(a,a)) 最右推导的分析树(包括推导过程中的分析树):
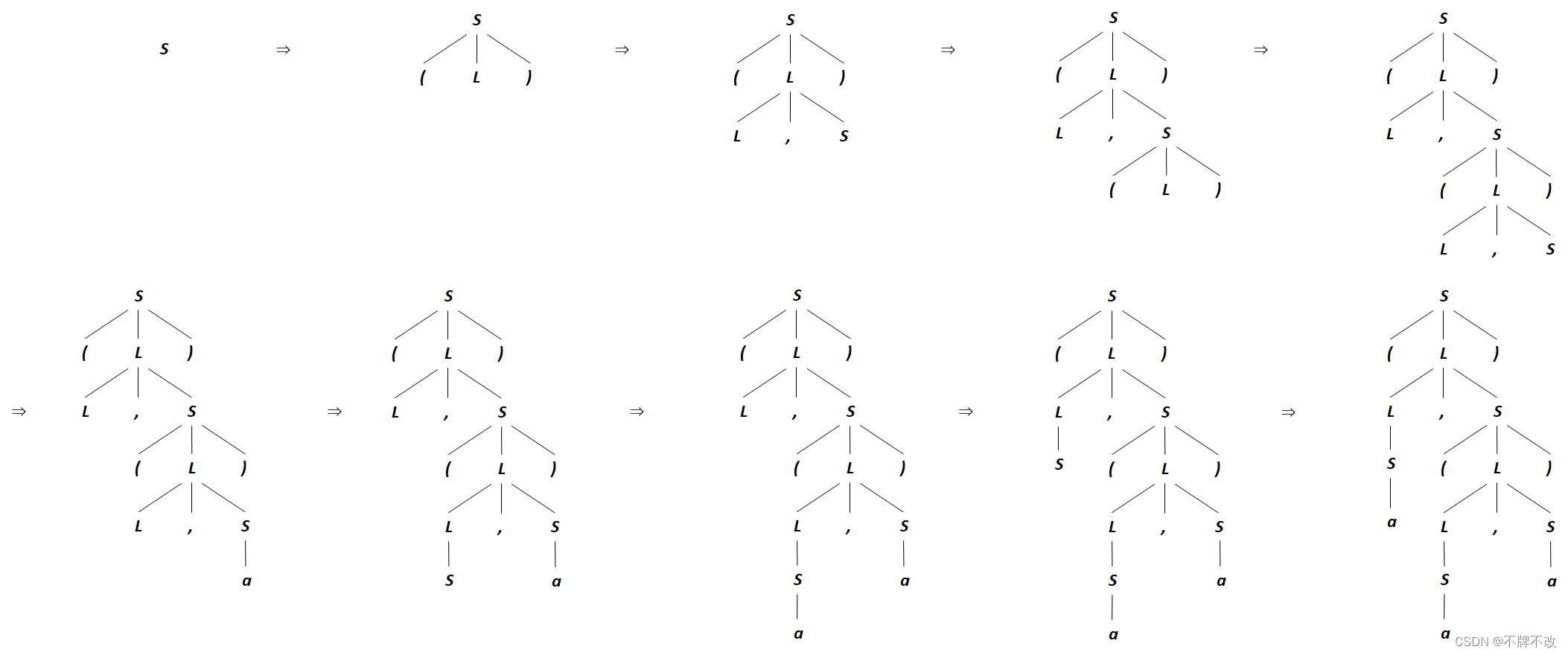
(
a
,
(
a
,
a
)
,
(
a
,
a
)
)
(a,(a,a),(a,a))
(a,(a,a),(a,a)) 最右推导:
S
⇒
r
m
(
L
)
⇒
r
m
(
L
,
S
)
⇒
r
m
(
L
,
(
L
)
)
⇒
r
m
(
L
,
(
L
,
S
)
)
⇒
r
m
(
L
,
(
L
,
(
L
)
)
)
⇒
r
m
(
L
,
(
L
,
(
L
,
S
)
)
)
⇒
r
m
(
L
,
(
L
,
(
L
,
a
)
)
)
⇒
r
m
(
L
,
(
L
,
(
S
,
a
)
)
)
⇒
r
m
(
L
,
(
L
,
(
a
,
a
)
)
)
⇒
r
m
(
L
,
(
S
,
(
a
,
a
)
)
)
⇒
r
m
(
L
,
(
(
L
)
,
(
a
,
a
)
)
)
⇒
r
m
(
L
,
(
(
L
,
S
)
,
(
a
,
a
)
)
)
⇒
r
m
(
L
,
(
(
L
,
a
)
,
(
a
,
a
)
)
)
⇒
r
m
(
L
,
(
(
S
,
a
)
,
(
a
,
a
)
)
)
⇒
r
m
(
L
,
(
(
a
,
a
)
,
(
a
,
a
)
)
)
⇒
r
m
(
S
,
(
(
a
,
a
)
,
(
a
,
a
)
)
)
⇒
r
m
(
a
,
(
(
a
,
a
)
,
(
a
,
a
)
)
)
S\Rightarrow_{rm} (L) \Rightarrow_{rm} (L,S) \Rightarrow_{rm} (L,(L)) \Rightarrow_{rm} (L,(L,S)) \Rightarrow_{rm} (L,(L,(L)))\Rightarrow_{rm} (L,(L,(L,S)))\Rightarrow_{rm} (L,(L,(L,a))) \\ \Rightarrow_{rm} (L,(L,(S,a))) \Rightarrow_{rm} (L,(L,(a,a))) \Rightarrow_{rm} (L,(S,(a,a))) \Rightarrow_{rm} (L,((L),(a,a)))\Rightarrow_{rm} (L,((L,S),(a,a))) \\ \Rightarrow_{rm} (L,((L,a),(a,a))) \Rightarrow_{rm} (L,((S,a),(a,a)))\Rightarrow_{rm} (L,((a,a),(a,a))) \Rightarrow_{rm} (S,((a,a),(a,a)))\Rightarrow_{rm} (a,((a,a),(a,a)))
S⇒rm(L)⇒rm(L,S)⇒rm(L,(L))⇒rm(L,(L,S))⇒rm(L,(L,(L)))⇒rm(L,(L,(L,S)))⇒rm(L,(L,(L,a)))⇒rm(L,(L,(S,a)))⇒rm(L,(L,(a,a)))⇒rm(L,(S,(a,a)))⇒rm(L,((L),(a,a)))⇒rm(L,((L,S),(a,a)))⇒rm(L,((L,a),(a,a)))⇒rm(L,((S,a),(a,a)))⇒rm(L,((a,a),(a,a)))⇒rm(S,((a,a),(a,a)))⇒rm(a,((a,a),(a,a)))
(d) 这个文法产生的语言是什么?
该文法产生的语言是括号匹配的串,串中的各项用“,”隔开,项可以是括号匹配的子串或 a。
T 3.2
考虑文法
S
→
a
S
b
S
∣
b
S
a
S
∣
ε
S\rightarrow aSbS\space|\space bSaS \space | \space \varepsilon
S→aSbS ∣ bSaS ∣ ε
**(a) 为句子
a
b
a
b
abab
abab 构造两个不同的最左推导,以此说明该文法是二义的。**
第一种最左推导的分析树(包括推导过程中的分析树):
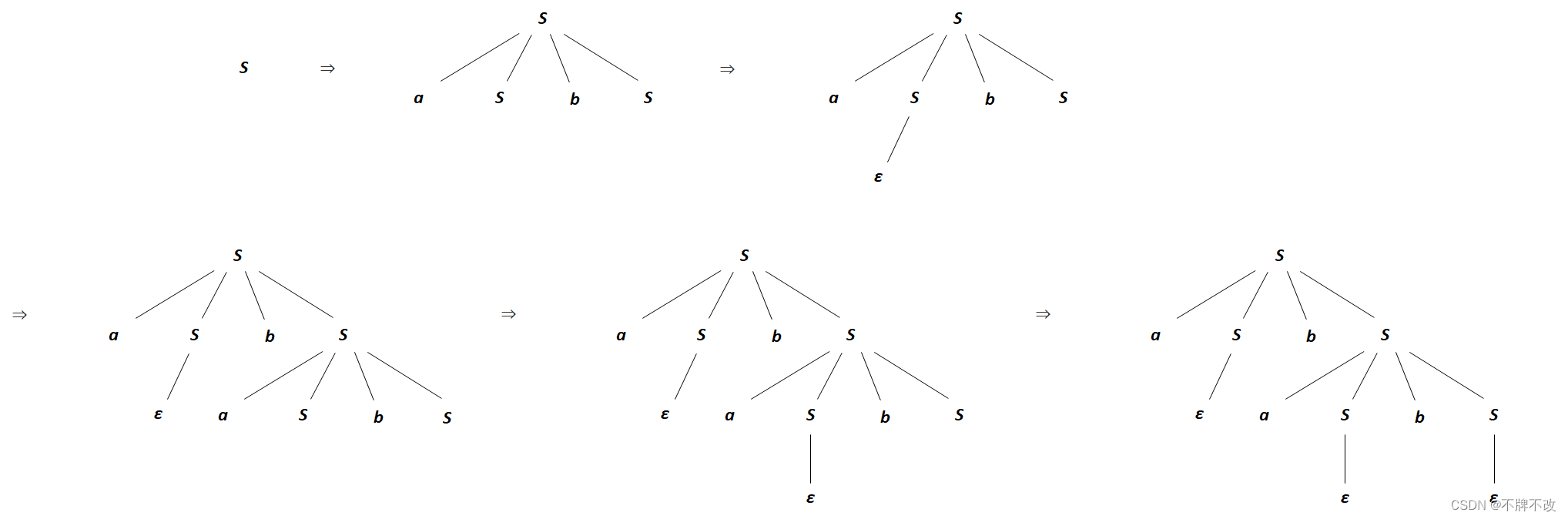
第二种最左推导的分析树(包括推导过程中的分析树):

一个文法,如果存在某个句子有不止一棵分析树与之对应,那么称这个文法是二义的;故,该文法是是二义的。
**(b) 为
a
b
a
b
abab
abab 构造对应的最右推导。**
两种最右推导的分析树(包括推导过程中的分析树)如下:
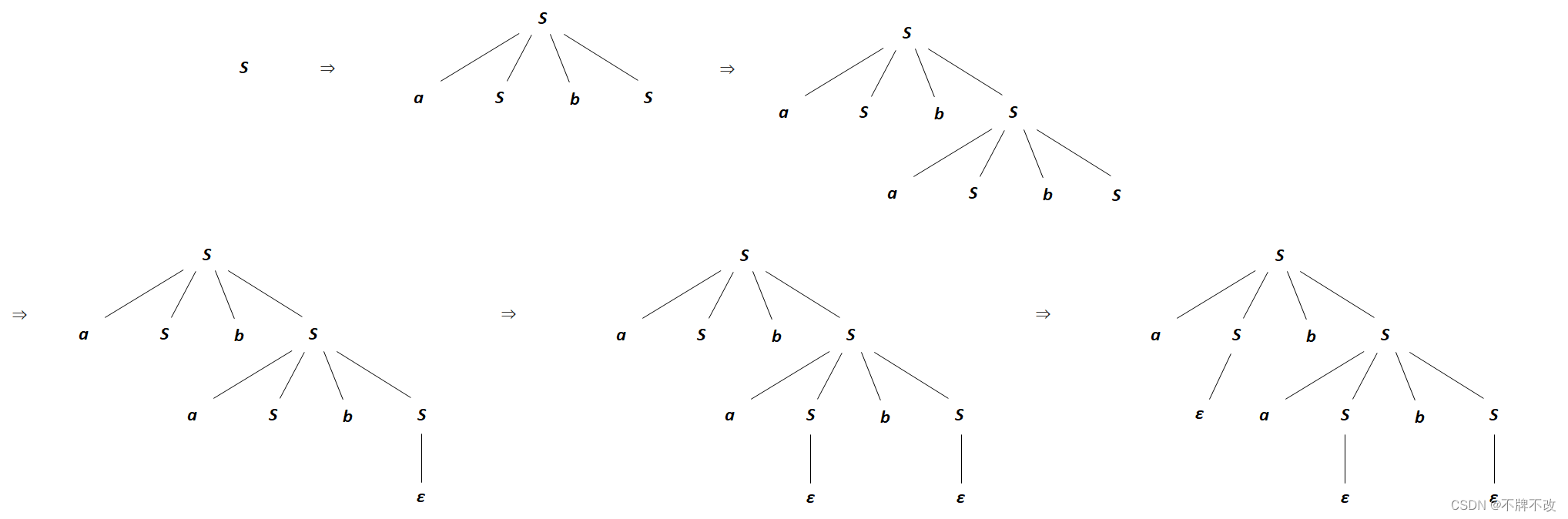

**(c) 为
a
b
a
b
abab
abab 构造对应的分析树。**
见上面四幅图。
(d) 这个文法产生的语言是什么?
通过最左推导的方式和产生式
S
→
a
S
b
S\rightarrow aSb
S→aSb 可以得到前缀为若干个
a
a
a 的任意长度的串;
通过最左推导的方式和产生式
S
→
b
S
a
S\rightarrow bSa
S→bSa 可以得到前缀为若干个
b
b
b 的任意长度的串;
题目给的产生式为
S
→
a
S
b
S
S\rightarrow aSbS
S→aSbS 、
S
→
b
S
a
S
S\rightarrow bSaS
S→bSaS 和
S
→
ε
S\rightarrow \varepsilon
S→ε,由
S
S
S 可以推导出空串,可以说明可以产生
S
→
a
S
b
S\rightarrow aSb
S→aSb 和
S
→
b
S
a
S\rightarrow bSa
S→bSa,因此由任意长度的前缀
a
a
a 和前缀
b
b
b 的子串可以构成
a
a
a 和
b
b
b 任意交错的串;
又因为每个产生式中
a
a
a 和
b
b
b 的个数都相同,**故产生
a
a
a 和
b
b
b 数目相等且任意长度的串**。
T 3.3
下面的二义文法描述命题演算公式,为它写一个等价的非二义性文法。
S
→
S
and
S
∣
S
or
S
∣
not
S
∣
true
∣
false
∣
(
S
)
S→S \space\textbf{and}\space S\space|\space S\space \textbf{or}\space S\space|\space \textbf{not}\space S\space|\space \textbf{true}\space|\space \textbf{false} \space|\space(S)
S→S and S ∣ S or S ∣ not S ∣ true ∣ false ∣ (S)
通过引入非终结符消除二义性:
E
→
E
or
T
∣
T
T
→
T
and
F
∣
F
F
→
not
F
∣
(
E
)
∣
true
∣
false
E\rightarrow E \textbf{or}\space T\space |\space T \\ T\rightarrow T \textbf{and}\space F\space |\space F \\ F\rightarrow \textbf{not} \space F\space |\space (E)\space |\space \textbf{true}\space |\space \textbf{false} \\
E→Eor T ∣ TT→Tand F ∣ FF→not F ∣ (E) ∣ true ∣ false
T 3.4
文法
R
→
R
′
∣
′
R
∣
R
R
∣
R
∗
∣
(
R
)
∣
a
∣
b
R\rightarrow R\space '|' \space R \space |\space R \space R \space|\space R^*\space|\space(R)\space|\space a \space | \space b
R→R ′∣′ R ∣ R R ∣ R∗ ∣ (R) ∣ a ∣ b
**产生字母表
{
a
,
b
}
\{a,b\}
{a,b} 上所有不含
ε
\varepsilon
ε 的正规式。注意,第一条竖线加了引号,它是正规式的或运算符号,而不是文法产生式右部各选择之间的分隔符,另外
∗
^*
∗在这里是一个普通的终结符。该文法是二义的。**
**(a) 证明该文法产生字母表
{
a
,
b
}
\{a,b\}
{a,b} 上的所有正规式。**
证明:
(1) 该文法产生的串是字母表
{
a
,
b
}
\{a,b\}
{a,b} 上的正规式:
R
→
a
R\rightarrow a
R→a和
R
→
b
R\rightarrow b
R→b产生
a
a
a和
b
b
b,而
a
a
a和
b
b
b是
{
a
,
b
}
\{a,b\}
{a,b}上的符号,因此是正规式。若
R
1
R_1
R1,
R
2
R_2
R2产生正规式
α
\alpha
α和
β
\beta
β
则:
R
→
R
1
R
2
R\rightarrow R_1R_2
R→R1R2 产生正规式
α
β
\alpha\beta
αβ
R
→
R
1
∣
R
2
R\rightarrow R_1|R_2
R→R1∣R2 产生正规式
α
∣
β
\alpha\space|\space\beta
α ∣ β
R
→
R
1
∗
R\rightarrow R_1^*
R→R1∗ 产生正规式
α
∗
\alpha^*
α∗
R
→
(
R
1
)
R\rightarrow (R_1)
R→(R1) 产生正规式
(
α
)
(\alpha)
(α)
(2) 字母表
{
a
,
b
}
\{a,b\}
{a,b} 上的所有正规式都可由此文法产生:
字母表
{
a
,
b
}
\{a,b\}
{a,b} 上的任一正规式(其中
α
\alpha
α,
β
\beta
β 为正规式)必为以下形式之一:
α
β
\alpha\beta
αβ,可由
R
→
R
R
R\rightarrow RR
R→RR 产生
α
∣
β
\alpha\space | \space\beta
α ∣ β,可由
R
→
R
∣
R
R\rightarrow R\space | \space R
R→R ∣ R 产生
α
∗
\alpha^*
α∗,可由
R
→
R
∗
R\rightarrow R^*
R→R∗ 产生
(
α
)
(\alpha)
(α),可由
R
→
(
R
)
R\rightarrow (R)
R→(R) 产生
a
a
a,可由
R
→
a
R\rightarrow a
R→a 产生
b
b
b,可由
R
→
b
R\rightarrow b
R→b 产生
因而,该文法产生字母表
{
a
,
b
}
\{a,b\}
{a,b} 上的所有正规式
**(b) 为该文法写一个等价的非二义文法。它给予算符
∗
^*
∗ 、连接和
∣
|
∣ 的优先级和结合性同 2.2 节中定义的一致。**
该文法没有体现运算符
∗
^*
∗ 、
(
)
()
()、
∣
|
∣ 和连接的优先级,因而是二义的。例如:
R
⇒
R
∣
R
⇒
a
∣
R
⇒
a
∣
R
∗
⇒
a
∣
b
∗
R
⇒
R
∗
⇒
R
∣
R
∗
⇒
a
∣
R
∗
⇒
a
∣
b
∗
R\Rightarrow R\space | \space R \Rightarrow a\space | \space R\space\Rightarrow a\space|\space R^*\Rightarrow a\space|\space b^* \\ R\Rightarrow R^* \Rightarrow R\space | \space R^*\space\Rightarrow a\space|\space R^*\Rightarrow a\space|\space b^*
R⇒R ∣ R⇒a ∣ R ⇒a ∣ R∗⇒a ∣ b∗R⇒R∗⇒R ∣ R∗ ⇒a ∣ R∗⇒a ∣ b∗
通过引入非终结符消除二义性:
E
→
E
′
∣
′
T
∣
T
T
→
T
F
∣
F
F
→
F
∗
∣
(
E
)
∣
a
∣
b
E\rightarrow E\space'|' \space T \space|\space T \\ T\rightarrow TF\space |\space F \\ F\rightarrow F^*\space | \space (E)\space |\space a \space |\space b
E→E ′∣′ T ∣ TT→TF ∣ FF→F∗ ∣ (E) ∣ a ∣ b
消除二义性后:
E
⇒
E
∣
T
⇒
E
∣
F
⇒
E
∣
F
∗
⇒
E
∣
b
∗
⇒
T
∣
b
∗
⇒
F
∣
b
∗
⇒
a
∣
b
∗
E\Rightarrow E\space|\space T\Rightarrow E\space|\space F\Rightarrow E\space|\space F^*\space\Rightarrow E\space |\space b^* \Rightarrow T\space | \space b^* \Rightarrow F \space | \space b^*\Rightarrow a \space | \space b^*
E⇒E ∣ T⇒E ∣ F⇒E ∣ F∗ ⇒E ∣ b∗⇒T ∣ b∗⇒F ∣ b∗⇒a ∣ b∗
**(c) 按上面两个文法构造句子
a
b
∣
b
∗
a
ab\space|\space b^*a
ab ∣ b∗a 的分析树。**
存在二义性:

不存在二义性:

T 3.5
条件语句文法
s
t
m
t
→
if
e
x
p
r
then
s
t
m
t
∣
m
a
t
c
h
e
d
_
s
t
m
t
m
a
t
c
h
e
d
_
s
t
m
t
→
if
e
x
p
r
then
m
a
t
c
h
e
d
_
s
t
m
t
else
s
t
m
s
t
∣
other
stmt \rightarrow \textbf{if}\space expr \space \textbf{then} \space stmt \space | \space matched\_stmt \\ matched\_stmt \rightarrow \textbf{if} \space expr \space \textbf{then} \space matched\_stmt\space \textbf{else} \space stmst \space | \space \textbf{other}
stmt→if expr then stmt ∣ matched_stmtmatched_stmt→if expr then matched_stmt else stmst ∣ other
**试图消除悬空
e
l
s
e
else
else 的二义性,请证明该文法仍然是二义的。**
由于
m
a
t
c
h
e
d
_
s
t
m
t
matched\_stmt
matched_stmt不能保证
t
h
e
n
then
then和
e
l
s
e
else
else的配对,因而存在二义性。
句型
i
f
e
x
p
r
t
h
e
n
i
f
e
x
p
r
t
h
e
n
m
a
t
c
h
e
d
_
s
t
m
t
e
l
s
e
i
f
e
x
p
r
t
h
e
n
m
a
t
c
h
e
d
_
s
t
m
t
e
l
s
e
s
t
m
t
if\space expr\space then \space if \space expr\space then \space matched\_stmt \space else \space if \space expr\space then \space matched\_stmt \space else \space stmt
if expr then if expr then matched_stmt else if expr then matched_stmt else stmt 存在两个不同的最左推导。
期望的是:
if expr then
if expr then
matched_stmt
else
if expr then
matched_stmt
else
stmt
一种和期望不一样的推导:
stmt
=> matched_stmt
=> if expr then matched_stmt else stmt
=> if expr then if expr then matched_stmt else stmt else stmt
=> if expr then if expr then matched_stmt else if expr then stmt else stmt
=> if expr then if expr then matched_stmt else if expr then matched_stmt else stmt
if expr then
if expr then
matched_stmt
else
if expr then
matched_stmt
else
stmt
另一种推导:
stmt
=> if expr then stmt
=> if expr then matched_stmt
=> if expr then if expr then matched_stmt else stmt
=> if expr then if expr then matched_stmt else matched_stmt
=> if expr then if expr then matched_stmt else if expr then matched_stmt else stmt
if expr then
if expr then
matched_stmt
else
if expr then
matched_stmt
else
stmt
T 3.8
(a) 消除习题 3.1 文法的左递归。
S
→
(
L
)
∣
a
L
→
S
L
′
L
′
→
,
S
L
′
∣
ε
S\rightarrow (L)\space | \space a \\ L\rightarrow SL' \\ L'\rightarrow\space ,SL'\space | \space \varepsilon
S→(L) ∣ aL→SL′L′→ ,SL′ ∣ ε
(b) 为 (a) 的文法构造预测分析器。
F
i
r
s
t
(
S
)
=
{
(
,
a
}
F
i
r
s
t
(
L
)
=
{
(
,
a
}
F
i
r
s
t
(
L
′
)
=
{
′
,
′
,
ε
}
F
o
l
l
o
w
(
S
)
=
{
)
,
′
,
′
,
$
}
F
o
l
l
o
w
(
L
)
=
{
)
,
$
}
F
o
l
l
o
w
(
L
′
)
=
{
)
,
$
}
First(S) = \{\space(\space,\space a\space\} \\ First(L) = \{\space(\space,\space a\space\} \\ First(L') = \{\space','\space,\space\varepsilon\space\} \\\\ Follow(S) = \{\space)\space,\space','\space,\space\$\space\} \\ Follow(L) = \{\space)\space, \space\$\space\} \\ Follow(L')= \{\space)\space, \space\$\space\} \\
First(S)={ ( , a }First(L)={ ( , a }First(L′)={ ′,′ , ε }Follow(S)={ ) , ′,′ , $ }Follow(L)={ ) , $ }Follow(L′)={ ) , $ }
非终结符输入符号()a,$SS→(L)S→aLL→SL'L→SL'L'L'→εL→,SL'L'→ε
T 3.10
构造下面文法的 LL(1) 分析表。
D
→
T
L
T
→
int
∣
real
L
→
id
R
R
→
,
id
R
∣
ε
D\rightarrow TL \\ T\rightarrow \textbf{int} \space | \space \textbf{real} \\ L\rightarrow \textbf{id} \space R \\ R\rightarrow\space ,\textbf{id}\space R \space | \space \varepsilon
D→TLT→int ∣ realL→id RR→ ,id R ∣ ε
先确定非终结符的
F
i
r
s
t
First
First 和
F
o
l
l
o
w
Follow
Follow 集:
F
i
r
s
t
(
D
)
=
F
i
r
s
t
(
T
)
=
{
int
,
real
}
F
i
r
s
t
(
L
)
=
{
id
}
F
i
r
s
t
(
R
)
=
{
′
,
′
,
ε
}
F
o
l
l
o
w
(
D
)
=
F
o
l
l
o
w
(
L
)
=
{
$
}
F
o
l
l
o
w
(
T
)
=
{
id
}
F
o
l
l
o
w
(
R
)
=
{
$
}
First(D)=First(T) = \{\textbf{int}, \textbf{real}\}\\ First(L)=\{\textbf{id}\} \\ First(R)=\{',', \varepsilon\} \\ \\ Follow(D)=Follow(L)=\{\$\} \\ Follow(T)=\{\textbf{id}\} \\ Follow(R)=\{\$\}
First(D)=First(T)={int,real}First(L)={id}First(R)={′,′,ε}Follow(D)=Follow(L)={$}Follow(T)={id}Follow(R)={$}
非终结符输入符号intrealid,$DD→TLD→TLTT→intT→realLL→idRRR→,idRR→ε
T 3.11
构造下面文法的 LL(1) 分析表。
S
→
a
B
S
∣
b
A
S
∣
ε
A
→
b
A
A
∣
a
B
→
a
B
B
∣
b
S\rightarrow aBS\space |\space bAS \space | \space \varepsilon \\ A\rightarrow bAA\space | \space a \\ B\rightarrow aBB \space | \space b
S→aBS ∣ bAS ∣ εA→bAA ∣ aB→aBB ∣ b
F
i
r
s
t
(
S
)
=
{
a
,
b
,
ε
}
F
i
r
s
t
(
A
)
=
F
i
r
s
t
(
B
)
=
{
a
,
b
}
F
o
l
l
o
w
(
S
)
=
F
o
l
l
o
w
(
A
)
=
F
o
l
l
o
w
(
B
)
=
{
$
}
First(S) = \{a, b, \varepsilon\}\\ First(A) = First(B) =\{a, b\} \\ \\ Follow(S)=Follow(A)=Follow(B)=\{\$\}
First(S)={a,b,ε}First(A)=First(B)={a,b}Follow(S)=Follow(A)=Follow(B)={$}
非终结符输入符号ab$SS→aBS
S→εS→bAS
S→εS→εAA→aA→bAABB→aBBB→b
T 3.12
下面的文法是否为 LL(1) 文法,说明理由。
S
→
A
B
∣
P
Q
x
A
→
x
y
B
→
b
c
P
→
d
P
∣
ε
Q
→
a
Q
∣
ε
S\rightarrow AB\space|\space PQx \\ A\rightarrow xy \\ B\rightarrow bc \\ P\rightarrow dP\space|\space \varepsilon\\ Q\rightarrow aQ\space | \space \varepsilon
S→AB ∣ PQxA→xyB→bcP→dP ∣ εQ→aQ ∣ ε
上面文法不是 LL(1) 文法。
LL(1) 文法:对于产生式
A
→
α
∣
β
A\rightarrow \alpha \space | \space \beta
A→α ∣ β 满足:
①
F
I
R
S
T
(
α
)
∩
F
I
R
S
T
(
β
)
=
ϕ
FIRST(\alpha)\space∩ \space FIRST(\beta) = \phi
FIRST(α) ∩ FIRST(β)=ϕ
② 若
β
⇒
∗
ε
\beta\Rightarrow ^* \varepsilon
β⇒∗ε ,那么
F
I
R
S
T
(
α
)
∩
F
o
l
l
o
w
(
A
)
=
ϕ
FIRST(\alpha)\space∩ \space Follow(A) = \phi
FIRST(α) ∩ Follow(A)=ϕ
而本题中,
F
I
R
S
T
(
A
B
)
=
{
x
}
FIRST(AB) = \{x\}
FIRST(AB)={x},
F
I
R
S
T
(
P
Q
x
)
=
{
d
,
a
,
x
}
FIRST(PQx) = \{d,a,x\}
FIRST(PQx)={d,a,x},不满足条件 ①,故,上面文法不是 LL(1) 文法。
T 3.18
为习题3.3的文法构造SLR分析表
扩展文法:



actiongotoandornottruefalse()$S0s2s3s4s511s6s7acc2s2s3s4s583r4r4r4r44r5r5r5r55s2s3s4s596s2s3s4s5107s2s3s4s5118s6/r3s7/r3r3r39s6s7r1210s6/r1s7/r1r1r111s6/r2s7/r2r2r212r6r6r6r6
T 3.29
(a) 为下面文法构造规范LR(1)分析表,画出像图3.20这样的状态转换图就可以。
S
→
V
=
E
∣
E
V
→
*
E
∣
id
E
→
V
S\rightarrow V\textbf{=}E\space|\space E\\ V\rightarrow \textbf{*}E\space|\space\textbf{id}\\ E\rightarrow V
S→V=E ∣ EV→*E ∣ idE→V
详述构建
I
0
I_0
I0的过程:
① 拓展文法:
S
′
→
S
(
0
)
S
→
V
=
E
(
1
)
S
→
E
(
2
)
V
→
*
E
(
3
)
V
→
id
(
4
)
E
→
V
(
5
)
S'\rightarrow S\space\space\space\space (0)\\ S\rightarrow V\textbf{=}E\space\space\space\space (1) \\ S\rightarrow E\space\space\space\space (2) \\ V\rightarrow \textbf{*}E\space\space\space\space (3) \\ V\rightarrow\textbf{id}\space\space\space\space (4)\\ E\rightarrow V \space\space\space\space (5)
S′→S (0)S→V=E (1)S→E (2)V→*E (3)V→id (4)E→V (5)
② 由于
S
′
S'
S′后面不会存在任何字符,所以其
F
o
l
l
o
w
Follow
Follow集中只有$元素,因此产生式(0)的搜索符为$

③ 对于项目
S
′
→
⋅
S
,
S'\rightarrow ·\space S\space, \space
S′→⋅ S , $
\space
,可以将产生式(1)代入,因为项目右部
S
S
S后面为空串,所以新项目的搜索符为$,故得到新项目
S
→
⋅
V
=
E
,
S\rightarrow·\space V\textbf{=}E\space, \space
S→⋅ V=E , $
\space
;类似地,将产生式(2)代入,得到新项目
S
→
⋅
E
,
S\rightarrow·\space E\space, \space
S→⋅ E , $

④ 对于项目
S
→
⋅
V
=
E
,
S\rightarrow·\space V\textbf{=}E\space, \space
S→⋅ V=E , $,可以将产生式(3)和(4)代入,因为项目右部
V
V
V后面为
=
=
=,所以新项目的搜索符为
=
=
=,而不是$,故得到新项目
V
→
⋅
*
E
,
=
V\rightarrow·\space\textbf{*}E\space, \space=
V→⋅ *E , =和
V
→
⋅
id
,
=
V\rightarrow·\space\textbf{id}\space, \space=
V→⋅ id , =

⑤ 对于项目
S
→
⋅
E
,
S\rightarrow·\space E\space, \space
S→⋅ E , $,可以将产生式(5)代入,因为项目右部
E
E
E后面为空串,所以新项目的搜索符为$,故得到新项目
S
→
⋅
V
,
S\rightarrow·\space V\space,\space
S→⋅ V , $

⑥ 项目
V
→
⋅
*
E
V\rightarrow ·\space\textbf{*}E
V→⋅ *E和
V
→
⋅
id
V\rightarrow· \space\textbf{id}
V→⋅ id 不会产生新的项目
⑦ 对于项目
S
→
⋅
V
,
S\rightarrow·\space V\space,\space
S→⋅ V , $,可以将产生式(3)和(4)代入,注意此时产生的新项目应该继承项目
S
→
⋅
V
,
S\rightarrow·\space V\space,\space
S→⋅ V , $的搜索符$,因此两个新项目为
V
→
⋅
*
E
,
V\rightarrow·\space\textbf{*}E\space, \space
V→⋅ *E , $和
V
→
⋅
id
,
V\rightarrow·\space\textbf{id}\space, \space
V→⋅ id , $

⑧ 不妨将第一个分量相同的项目对应的搜索符集合合并一下

生成其他状态的道理类似,只展示结果。


(b) 上述状态转换图有同心项目集吗?若有,合并同心项目集后是否会出现动作冲突?
其中
I
4
I_4
I4和
I
11
I_{11}
I11、
I
5
I_5
I5和
I
12
I_{12}
I12、
I
7
I_7
I7和
I
13
I_{13}
I13、
I
8
I_8
I8和
I
10
I_{10}
I10分别为同心项目集。
同心项目集的合并(又得到LALR自动机的过程)不会引入新的移进-归约冲突,可能会引入新的归约-归约冲突;又因为规范LR(1)自动机已经解决了移进-归约冲突的问题,所以只需要验证是否存在归约-归约冲突即可。显然合并后不存在归约-归约冲突,综上,不存在动作冲突。
版权归原作者 不牌不改 所有, 如有侵权,请联系我们删除。