【算法】详解 “清华大学（考研）OJ题”_ 二叉树重要面试OJ题

💛 前情提要💛

本章节是

数据结构

的

二叉树重要面试OJ题

的相关知识~

接下来我们即将进入一个全新的空间，对代码有一个全新的视角~

以下的内容一定会让你对

数据结构

有一个颠覆性的认识哦！！！

❗以下内容以

C语言

的方式实现，对于

数据结构

来说最重要的是

思想

哦❗

以下内容干货满满，跟上步伐吧~

作者介绍：

🎓 作者： 热爱编程不起眼的小人物🐐
🔎作者的Gitee：代码仓库
📌系列文章&专栏推荐： 《刷题特辑》、 《C语言学习专栏》、《数据结构_初阶》

📒我和大家一样都是初次踏入这个美妙的“元”宇宙🌏 希望在输出知识的同时，也能与大家共同进步、无限进步🌟

🌐为大家推荐一款刷题网站呀👉点击跳转
以下题目&算法思想，都可以从此网站中找到并参考学习哟~

📌导航小助手📌

💡本章重点

• 二叉树的层序遍历
• 二叉树重要面试OJ题
• 🔥算法思想

🍞一.广度优先遍历

🥐Ⅰ.层序遍历

💡广度优先遍历： 对于二叉树来说又称为

层序遍历

• 即访问顺序不同与先序、中序、后序遍历【这三种遍历统称为：深度优先遍历】要递归访问完一个分支后才返回再递归访问剩下的分支
• 而层序遍历就是一层一层的遍历树的结点，遍历完一层后，才遍历下一层，直至遍历完整棵树

❗特别注意：

• 对于广度优先遍历，我们一般借助队列的数据结构去实现 【对于>队列<的知识有遗忘的，可以点击跳转食用哟~】
• 在遍历完后，切记对队列所申请的空间进行释放，以防止内存泄露的情况

➡️实现方式：

• 1️⃣先将第一层的树的结点入队列
• 2️⃣当队列不为NULL时，可以借助队列FIFO（先进先出）原则，进行对已经入队列的树的结点依次读取（达到访问结点的效果）并删除在队列中已经访问过的结点
• 3️⃣在上述删除某个结点的同时，将此结点的孩子结点插入队列中（即相当于同时对下一层进行处理，以达到访问完这一层后，可以继续访问孩子节点所在的层）
• 4️⃣重复上述步骤，直至队列为NULL，代表整棵树已完全遍历

✊动图示例：

👉代码实现：

1️⃣实现

队列

的数据结构：

typedefint QDataType;typedefstruct QueueNode
{struct QueueNode* next;
    QDataType data;}QNode;typedefstruct Queue
{//int size;
    QNode* head;
    QNode* tail;}Queue;voidQueueInit(Queue* pq);voidQueueDestroy(Queue* pq);voidQueuePush(Queue* pq, QDataType x);voidQueuePop(Queue* pq);
QDataType QueueFront(Queue* pq);
QDataType QueueBack(Queue* pq);boolQueueEmpty(Queue* pq);intQueueSize(Queue* pq);voidQueueInit(Queue* pq){assert(pq);
    pq->head = pq->tail =NULL;}voidQueueDestroy(Queue* pq){assert(pq);
    QNode* cur = pq->head;while(cur){
        QNode* next = cur->next;free(cur);
        cur = next;}

    pq->head = pq->tail =NULL;}voidQueuePush(Queue* pq, QDataType x){assert(pq);
    QNode* newnode =(QNode*)malloc(sizeof(QNode));if(newnode ==NULL){printf("malloc fail\n");exit(-1);}
    newnode->data = x;
    newnode->next =NULL;if(pq->tail ==NULL){
        pq->head = pq->tail = newnode;}else{
        pq->tail->next = newnode;
        pq->tail = newnode;}}voidQueuePop(Queue* pq){assert(pq);assert(!QueueEmpty(pq));if(pq->head->next ==NULL){free(pq->head);
        pq->head = pq->tail =NULL;}else{
        QNode* next = pq->head->next;free(pq->head);
        pq->head = next;}}

QDataType QueueFront(Queue* pq){assert(pq);assert(!QueueEmpty(pq));return pq->head->data;}

QDataType QueueBack(Queue* pq){assert(pq);assert(!QueueEmpty(pq));return pq->tail->data;}boolQueueEmpty(Queue* pq){assert(pq);return pq->head ==NULL;}intQueueSize(Queue* pq){assert(pq);
    QNode* cur = pq->head;int size =0;while(cur){++size;
        cur = cur->next;}return size;}

2️⃣实现层序遍历：

voidTreeLevelOrder(BTNode* root){
    Queue q;QueueInit(&q);if(root){QueuePush(&q, root);}while(!QueueEmpty(&q)){
        BTNode* front =QueueFront(&q);QueuePop(&q);printf("%d ", front->data);if(front->left !=NULL){QueuePush(&q, front->left);}if(front->right !=NULL){QueuePush(&q, front->right);}}QueueDestroy(&q);}

🥯Ⅱ.总结

✨综上：就是

层序遍历

啦~

➡️相信大家对新的遍历方式有不一样的看法了吧🧡

🍞二.二叉树重要面试OJ题

🔥秒杀模板

❗ 秒杀口诀：

• 左右子树之间的逻辑关系➕树的遍历方式

❓忘记的同学可以>点击<前往回顾呀

✊让我们用题目来实际运用分析吧~

🏷️ 二叉树的前序遍历【难度：简单】

🔍题目传送门：
牛客网：BM23. 二叉树的前序遍历

🌐更多同类题型，不同算法思想学习，可点击>网站跳转<呀😉

给你二叉树的根节点

root

，返回它节点值的

前序

遍历。

• 示例 1：

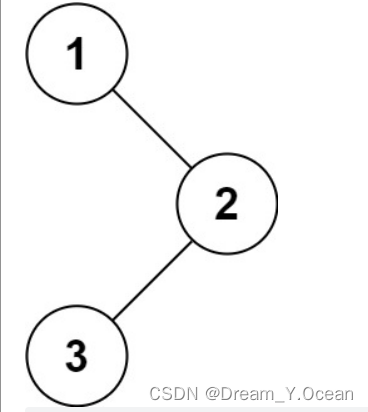
输入：root =[1,null,2,3]
输出：[1,2,3]

• 示例 2：

输入：root =[]
输出：[]

• 示例 3：

输入：root =[1]
输出：[1]

💡解题关键：

• 我们需要知道前序遍历的遍历方式
• 本题就可以运用我们的秒杀技巧

❗特别注意：

• 本题中我们需要将前序遍历得到的结点存入数组中，我们便需要提前得知此数组需要开辟多大的空间【即需要知道树的结点个数】

👉秒杀分析：

• 计算树的结点个数时，整棵树（分为根节点、左子树、右子树）来看就是：左子树总的结点个数 + 右子树总的结点个数 + 1（根节点）
• 所以逻辑关系为：+

👆综上：

• 秒杀口诀为：+➕后序遍历
• 本质：利用递归的性质，先计算左子树总的结点个数，再计算右子树总的结点个数，最终返回的是左子树与右子树总的结点个数的和 + 1（根节点自身个数）

✊动图示例：

👉代码实现：

inttreeSize(struct TreeNode* root){return root ==NULL?0:treeSize(root->left)+treeSize(root->right)+1;}voidpreorder(struct TreeNode* root,int*arr,int* i){//前序遍历if(root ==NULL){return;}

    arr[(*i)++]= root->val;preorder(root->left, arr, i);preorder(root->right, arr, i);}int*preorderTraversal(struct TreeNode* root,int* returnSize){*returnSize =treeSize(root);int* arr =(int*)malloc(sizeof(int)*(*returnSize));int i =0;preorder(root, arr,&i);return arr;}

➡️补充：

• 我们需要带着自己开辟的数组和数组下标进行前序遍历，因为需要将遍历得到的结点存入数组中
• 所以每一次下标的改变都需要让不同的递归栈帧知道，所以下标需要传的是地址（否则如果传的是下标的临时拷贝，那数组内的结点之间就会造成覆盖）

🏷️ 另一棵树的子树【难度：简单】

🔍题目传送门：
Leetcode：572. 另一棵树的子树
给你两棵二叉树

root

和

subRoot

。检验

root

中是否包含和

subRoot

具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false

二叉树

tree

的一棵子树包括

tree

的某个节点和这个节点的所有后代节点。

tree

也可以看做它自身的一棵子树

示例 1：

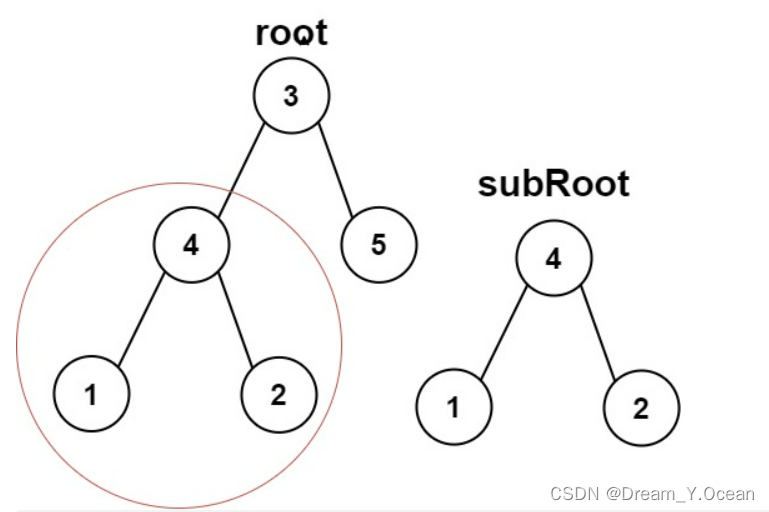
输入：root =[3,4,5,1,2], subRoot =[4,1,2]
输出：true

示例 2：

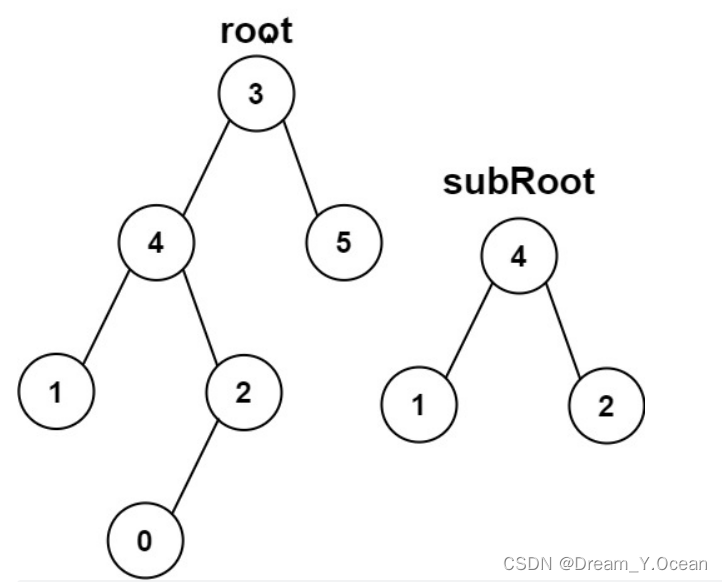
输入：root =[3,4,5,1,2,null,null,null,null,0], subRoot =[4,1,2]
输出：false

💡解题关键：

• 遍历主树的每一个结点，让每一个结点当作根节点时，去判断此时的根节点的树是否与子树相同
• 此时我们便可以复用检查两棵树是否相同的代码进行判断

👉秒杀分析：

• 因为需要遍历主树的每一个结点，让其每一个结点当根节点时的树去与子树判断是否相同
• 所以我们对主树采取前序遍历【即这样遍历下，我们可以快速且从上往下全面的判断是否为子树】，若为其余遍历方式，则可能一开始就错过导致程序做了一些无用功
• 又因为只要主树里一旦找到为子树的情况，就无需继续找子树了，所以逻辑关系为||【即主树的某个结点为树时是子树的情况，返回true，逻辑关系||遇上true就可以直接停止寻找】

➡️做题思路：

• 用前序遍历遍历主树每一个结点，让每一个结点当作根节点去作树，与需要判断的子树判断两棵树是否相同
• 一旦找到，就返回true，停止寻找

✊动图示例：

👉代码实现：

bool isSameTree(struct TreeNode* p,struct TreeNode* q){//1.树都为NULL的时候 -- 相等//2.比较比到 NULL 的时候 == 前面都比完了，那就相等if(p ==NULL&& q ==NULL){return true;}//判断p树和q树结构是否相同if(p ==NULL|| q ==NULL){return false;}//结构相同，再去判断值if(p->val != q->val){return false;}returnisSameTree(p->left, q->left)&&isSameTree(p->right, q->right);}

bool isSubtree(struct TreeNode* root,struct TreeNode* subRoot){//遍历root这棵树的每个结点，每个结点做子树根 ，去跟subRoot比较if(root ==NULL){return false;}if(isSameTree(root, subRoot)){return true;}returnisSubtree(root->left, subRoot)||isSubtree(root->right, subRoot);}

🏷️ 平衡二叉树【难度：简单】

🔍题目传送门：
Leetcode：110. 平衡二叉树
给定一个二叉树，判断它是否是高度平衡的二叉树

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1

• 示例 1：

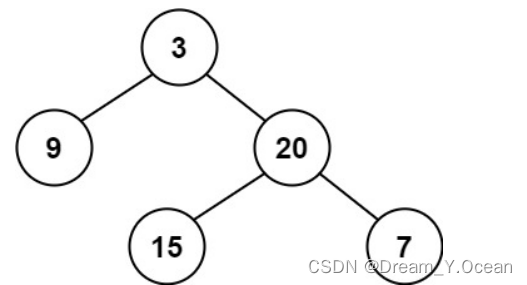
输入：root =[3,9,20,null,null,15,7]
输出：true

• 示例 2：

输入：root =[1,2,2,3,3,null,null,4,4]
输出：false

• 示例 3：

输入：root =[]
输出：true

💡解题关键：

• 我们需要遍历树中的每一个结点，并让此结点作为根节点去看作一棵树，并比较此树的左右子树的高度是否平衡

👉秒杀分析：

• 对于树中的每一个结点为根节点看作一棵树时，都需要时刻满足平衡条件，所以逻辑关系采用&&【即递归判断子树是否平衡时，只要一个不满足返回false，那整体就直接停止判断并返回false表示不平衡】
• 而遍历树中每一个结点时，我们采用前序遍历，这样一旦判断当前不满足平衡条件，就不需要判断后面的了
• 综上，秒杀口诀为：&&➕前序遍历

❗特别注意：

• 对于获取二叉树最大深度，我们采用的秒杀口诀为：后序遍历➕比较获取最大深度
• 在比较获取最大深度中，+1表示所获取子树的层数加上当前树的根节点的这一层

✊动图示例：

👉代码实现：

intmaxDepth(struct TreeNode* root){if(root ==NULL){return0;}int leftDepth =maxDepth(root->left);int rightDepth =maxDepth(root->right);return leftDepth > rightDepth ? leftDepth +1: rightDepth +1;}

bool isBalanced(struct TreeNode* root){if(root ==NULL){return true;}int leftDepth =maxDepth(root->left);int rightDepth =maxDepth(root->right);returnabs(leftDepth - rightDepth)<2&&isBalanced(root->left)&&isBalanced(root->right);}

🏷️ 二叉树的构建及遍历（清华大学）【难度：较难】

❗此题曾为

清华大学

OJ题，同学们一定要细心感受这一道题目哟❗

🔍题目传送门：
牛客网：KY11. 二叉树的构建及遍历

🌐更多同类题型，不同算法思想学习，可点击>网站跳转<呀😉

编一个程序，读入用户输入的一串先序遍历字符串，根据此字符串建立一个二叉树（以指针方式存储）。

例如如下的先序遍历字符串： ABC##DE#G##F###

其中

#

表示的是

空格

，

空格字符

代表

空树

。

建立起此二叉树以后，再对二叉树进行

中序遍历

，输出遍历结果

• 示例 1：

输入：abc##de#g##f###
输出：c b e g d f a 

💡解题关键：

• 利用二叉树本质是：递归式，从而利用递归去建立二叉树

➡️做题分析：

本质运用的是：

前序遍历

• 1️⃣构建根结点
• 控制数组下标去遍历字符串，判断当前为什么字符- 如果是#，则数组下标++【继续往后遍历】，并返回NULL- 若不是#，则创建一个二叉树的结点去存储当前字符，并让数组下标++【继续往后遍历】
• 2️⃣开始构建左右子树，并链接
• 先递归构建左子树【即回到步骤1️⃣】，递归返回的时候再开始链接结点
• 再递归构建右子树【即回到步骤1️⃣】，递归返回的时候再开始链接结点
• 3️⃣最后返回这棵二叉树的根节点

❗特别注意：

• 上述的链接结点的步骤，因为是由递归去构建二叉树的，所以本质是从二叉树的底部开始往上链接【即从NULL开始往上链接各个结点，直至构建成一棵树】
• 因为赋值运算符的结合性是从右往左，这也是为什么先执行递归，返回的时候再链接结点

✊动图示例：

👉代码实现：

#include<stdio.h>#include<stdlib.h>typedefstruct TreeNode
{struct TreeNode* left;struct TreeNode* right;char val;}TreeNode;//构建二叉树
TreeNode*CreateTree(char*str,int* i){if(str[*i]=='#'){(*i)++;//如果一上来就是#，则有可能是空树returnNULL;}
    
    TreeNode* root =(TreeNode*)malloc(sizeof(TreeNode));
    root->val = str[*i];(*i)++;//递归构建左子树，然后链接
    root->left =CreateTree(str, i);//递归构建右子树，然后链接
    root->right =CreateTree(str,i);return root;}//中序遍历voidInorder(TreeNode* root){if(root ==NULL){return;}Inorder(root->left);printf("%c ",root->val);Inorder(root->right);}intmain(){char str[101]={0};scanf("%s",str);//i表示下标int i =0;//创建树
    TreeNode* root =CreateTree(str,&i);//中序遍历Inorder(root);printf("\n");return0;}

🥯总结

✨综上：就是

二叉树重要面试OJ题

的相关内容啦~

➡️相信大家对这些题目了如指掌了吧，也十分建议同学们多多练习中间的思想哟🧡

🫓总结

综上，我们基本了解了数据结构中的 “二叉树重要面试OJ题” 🍭 的知识啦~~

恭喜你的内功又双叒叕得到了提高！！！

感谢你们的阅读😆

后续还会继续更新💓，欢迎持续关注📌哟~

💫如果有错误❌，欢迎指正呀💫

✨如果觉得收获满满，可以点点赞👍支持一下哟~✨