0
0

11种经典时间序列预测方法：理论、Python实现与应用

时间序列分析和预测在现代数据科学中扮演着关键角色，广泛应用于金融、经济、气象学和工程等领域。本文将总结11种经典的时间序列预测方法，并提供它们在Python中的实现示例。

这些方法包括：

  1. 自回归（AR）
  2. 移动平均（MA）
  3. 自回归移动平均（ARMA）
  4. 自回归积分移动平均（ARIMA）
  5. 季节性自回归积分移动平均（SARIMA）
  6. 具有外生回归量的季节性自回归积分移动平均（SARIMAX）
  7. 向量自回归（VAR）
  8. 向量自回归移动平均（VARMA）
  9. 具有外生回归量的向量自回归移动平均（VARMAX）
  10. 简单指数平滑（SES）
  11. Holt-Winters指数平滑（HWES）

本文利用Python的Statsmodels库实现这些方法。Statsmodels提供了强大而灵活的工具，用于统计建模和计量经济学分析。

1、自回归（AR）模型

自回归（AR）模型是时间序列分析中的基础模型之一。它假设序列中的每个观测值都可以表示为其前p个观测值的线性组合加上一个随机误差项。

数学表示

AR(p)模型可以表示为：

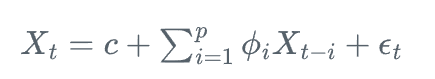
其中，X_t是t时刻的观测值，c是常数项，\phi_i是自回归系数，\epsilon_t是白噪声。

优势

  • 模型简单，易于理解和实现
  • 适用于具有短期依赖性的时间序列
  • 计算效率高

局限性

  • 假设时间序列是平稳的
  • 无法捕捉复杂的非线性模式
  • 不适用于具有明显趋势或季节性的数据

适用场景

  • 金融市场的短期价格波动预测
  • 气象数据的短期预测
  • 经济指标的短期预测

参数解释

  • p：自回归阶数，表示模型考虑的历史观测值数量
  • 自回归系数\phi_i：表示过去观测值对当前值的影响程度

Python实现

 fromstatsmodels.tsa.ar_modelimportAutoReg
 fromrandomimportrandom
 
 # 生成示例数据
 data= [x+random() forxinrange(1, 100)]
 
 # 拟合AR模型
 model=AutoReg(data, lags=1)
 model_fit=model.fit()
 
 # 进行预测
 yhat=model_fit.predict(len(data), len(data))
 print(yhat)

模型诊断

  • 自相关函数（ACF）和偏自相关函数（PACF）图
  • AIC（赤池信息准则）和BIC（贝叶斯信息准则）
  • 残差分析：检查残差的白噪声性质

2. 移动平均（MA）模型

移动平均（MA）模型假设时间序列的当前值可以表示为当前和过去的白噪声误差项的线性组合。

数学表示

MA(q)模型可以表示为：

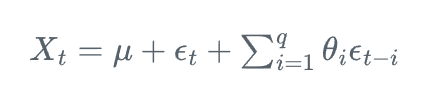
其中，X_t是t时刻的观测值，\mu是期望值，\theta_i是移动平均系数，\epsilon_t是白噪声。

优势

  • 适合模拟短期波动
  • 可以处理某些非平稳序列
  • 对异常值的敏感性较低

局限性

  • 无法捕捉长期趋势
  • 参数估计可能较为复杂
  • 不适用于具有明显趋势或季节性的数据

适用场景

  • 金融市场的短期波动分析
  • 质量控制中的过程监控
  • 信号处理中的噪声滤除

参数解释

  • q：移动平均阶数，表示模型考虑的过去白噪声误差项数量
  • 移动平均系数\theta_i：表示过去白噪声误差对当前值的影响程度

Python实现

 fromstatsmodels.tsa.arima.modelimportARIMA
 fromrandomimportrandom
 
 # 生成示例数据
 data= [x+random() forxinrange(1, 100)]
 
 # 拟合MA模型
 model=ARIMA(data, order=(0, 0, 1))
 model_fit=model.fit()
 
 # 进行预测
 yhat=model_fit.predict(len(data), len(data))
 print(yhat)

模型诊断

  • ACF和PACF图分析
  • 残差的正态性检验
  • Ljung-Box测试检验残差的独立性

3、自回归移动平均（ARMA）模型

自回归移动平均（ARMA）模型结合了自回归（AR）和移动平均（MA）模型的特性，能够同时捕捉时间序列的自相关性和移动平均特性。

数学表示

ARMA(p,q)模型可以表示为：

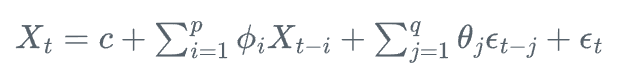
其中，X_t是t时刻的观测值，c是常数项，\phi_i是自回归系数，\theta_j是移动平均系数，\epsilon_t是白噪声。

优势

  • 比单纯的AR或MA模型更灵活
  • 可以描述更复杂的时间序列模式
  • 在许多实际应用中表现良好

局限性

  • 假设时间序列是平稳的
  • 参数估计可能较为复杂
  • 可能存在模型识别的困难（选择合适的p和q值）

适用场景

  • 经济指标预测
  • 股票市场分析
  • 工业生产过程控制

参数解释

  • p：自回归项的阶数
  • q：移动平均项的阶数
  • 自回归系数\phi_i和移动平均系数\theta_j：分别表示过去观测值和过去误差对当前值的影响程度

Python实现

 fromstatsmodels.tsa.arima.modelimportARIMA
 fromrandomimportrandom
 
 # 生成示例数据
 data= [random() forxinrange(1, 100)]
 
 # 拟合ARMA模型
 model=ARIMA(data, order=(2, 0, 1))
 model_fit=model.fit()
 
 # 进行预测
 yhat=model_fit.predict(len(data), len(data))
 print(yhat)

模型诊断

  • AIC和BIC准则用于模型选择
  • 残差分析：检查残差的白噪声性质和正态性
  • 过拟合测试：比较不同阶数模型的性能

4、自回归积分移动平均（ARIMA）模型

自回归积分移动平均（ARIMA）模型是ARMA模型的推广，通过引入差分操作来处理非平稳时间序列。它结合了差分（I）、自回归（AR）和移动平均（MA）三个组件。

数学表示

ARIMA(p,d,q)模型可以表示为：

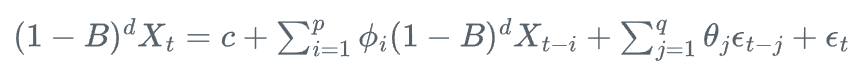
其中，B是后移算子，d是差分阶数，其他符号含义与ARMA模型相同。

优势

  • 可以处理非平稳时间序列
  • 能够捕捉复杂的时间序列模式
  • 适用于具有趋势的数据

局限性

  • 对异常值敏感
  • 可能不适合处理强烈的季节性模式
  • 参数选择可能较为复杂

适用场景

  • 经济和金融数据分析，如GDP增长率预测
  • 销售额预测
  • 气象数据分析

参数解释

  • p：自回归项的阶数
  • d：差分阶数
  • q：移动平均项的阶数

Python实现

 fromstatsmodels.tsa.arima.modelimportARIMA
 fromrandomimportrandom
 
 # 生成示例数据
 data= [x+random() forxinrange(1, 100)]
 
 # 拟合ARIMA模型
 model=ARIMA(data, order=(1, 1, 1))
 model_fit=model.fit()
 
 # 进行预测
 yhat=model_fit.predict(len(data), len(data), typ='levels')
 print(yhat)

模型诊断

  • 单位根检验：确保差分后的序列是平稳的
  • ACF和PACF图分析：辅助确定p和q的值
  • 残差分析：检查残差的独立性和正态性
  • 预测性能评估：使用均方根误差（RMSE）或平均绝对误差（MAE）等指标

扩展和变体

  • 季节性ARIMA（SARIMA）：引入季节性成分
  • ARIMAX：包含外生变量的ARIMA模型
  • 分数阶ARIMA：允许非整数阶差分

实施注意事项

  • 数据预处理：处理缺失值和异常值
  • 模型选择：使用网格搜索或信息准则（如AIC、BIC）选择最佳参数
  • 模型验证：使用交叉验证或滚动预测评估模型性能
  • 定期重估：在新数据可用时更新模型参数

ARIMA模型是时间序列分析中最常用和最强大的工具之一。它的灵活性使其能够适应各种不同类型的时间序列数据，但同时也要求分析者具有丰富的经验和专业知识来正确指定和解释模型。在实际应用中，通常需要结合领域知识、统计诊断和试验来选择最佳的模型规格。

5、季节性自回归积分移动平均（SARIMA）模型

季节性自回归积分移动平均（SARIMA）模型是ARIMA模型的扩展，专门用于处理具有季节性模式的时间序列数据。它在ARIMA模型的基础上增加了季节性成分。

数学表示

SARIMA(p,d,q)(P,D,Q)m模型可以表示为：

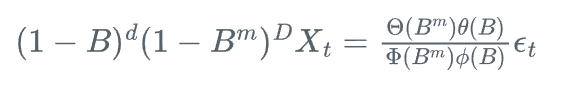
其中，B是后移算子，m是季节性周期，\phi(B)和\theta(B)分别是非季节性AR和MA多项式，\Phi(B^m)和\Theta(B^m)分别是季节性AR和MA多项式。

优势

  • 可以处理具有季节性模式的时间序列
  • 能够捕捉复杂的时间依赖结构
  • 适用于多种具有周期性的数据

局限性

  • 模型复杂度高，参数估计可能困难
  • 需要较长的时间序列才能得到可靠的季节性估计
  • 可能对异常值敏感

适用场景

  • 季节性销售数据预测
  • 旅游业客流量分析
  • 能源消耗预测

参数解释

  • p, d, q：非季节性ARIMA阶数
  • P, D, Q：季节性ARIMA阶数
  • m：季节性周期长度

Python实现

 fromstatsmodels.tsa.statespace.sarimaximportSARIMAX
 fromrandomimportrandom
 
 # 生成示例数据
 data= [x+random() forxinrange(1, 100)]
 
 # 拟合SARIMA模型
 model=SARIMAX(data, order=(1, 1, 1), seasonal_order=(1, 1, 1, 12))
 model_fit=model.fit(disp=False)
 
 # 进行预测
 yhat=model_fit.predict(len(data), len(data))
 print(yhat)

模型诊断

  • 季节性和趋势分解
  • ACF和PACF图分析（考虑季节性滞后）
  • AIC和BIC用于模型选择
  • 残差分析：检查季节性残差的白噪声性质

6、具有外生回归量的季节性自回归积分移动平均（SARIMAX）模型

SARIMAX模型是SARIMA模型的进一步扩展，它允许在模型中包含外生变量（也称为协变量或回归量）。这使得模型能够考虑额外的解释变量对时间序列的影响。

数学表示

SARIMAX模型可以表示为：

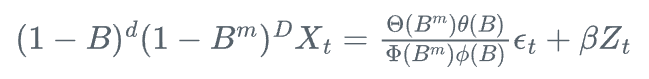
其中，Z_t是外生变量，\beta是相应的系数。

优势

  • 可以纳入额外的解释变量
  • 提高预测精度，特别是当外生变量与因变量高度相关时
  • 能够捕捉复杂的时间依赖结构和外部影响

局限性

  • 模型复杂度更高，可能面临过拟合风险
  • 需要准确预测外生变量才能进行长期预测
  • 参数估计和模型选择更为复杂

适用场景

  • 考虑天气因素的能源需求预测
  • 包含经济指标的销售预测
  • 考虑多个影响因素的金融市场分析

参数解释

与SARIMA模型相同，额外包括：

  • 外生变量的系数\beta

Python实现

 fromstatsmodels.tsa.statespace.sarimaximportSARIMAX
 fromrandomimportrandom
 
 # 生成示例数据
 data1= [x+random() forxinrange(1, 100)]
 data2= [x+random() forxinrange(101, 200)]  # 外生变量
 
 # 拟合SARIMAX模型
 model=SARIMAX(data1, exog=data2, order=(1, 1, 1), seasonal_order=(1, 1, 1, 12))
 model_fit=model.fit(disp=False)
 
 # 进行预测
 exog2= [200+random()]  # 用于预测的外生变量值
 yhat=model_fit.predict(len(data1), len(data1), exog=[exog2])
 print(yhat)

模型诊断

  • 外生变量的显著性检验
  • 多重共线性检查
  • 预测性能评估：比较包含和不包含外生变量的模型

7. 向量自回归（VAR）模型

向量自回归（VAR）模型是用于多变量时间序列分析的统计模型。它将每个变量表示为其自身滞后值和其他变量滞后值的线性函数。

数学表示

VAR(p)模型可以表示为：

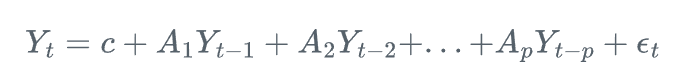
其中，Y_t是k维随机向量，c是k维常数向量，A_i是k×k系数矩阵，\epsilon_t是k维白噪声向量。

优势

  • 可以捕捉多个变量之间的相互作用
  • 允许进行系统的冲击响应分析
  • 适用于预测相互关联的时间序列

局限性

  • 参数数量随变量数量的增加而迅速增加
  • 假设变量之间的关系是线性的
  • 可能面临过度参数化的问题

适用场景

  • 宏观经济指标分析
  • 金融市场不同资产类别之间的相互影响研究
  • 多维度销售数据预测

参数解释

  • p：滞后阶数
  • k：变量数量
  • 系数矩阵A_i：表示不同变量之间的相互影响

Python实现

 fromstatsmodels.tsa.vector_ar.var_modelimportVAR
 fromrandomimportrandom
 
 # 生成示例多变量数据
 data=list()
 foriinrange(100):
     v1=i+random()
     v2=v1+random()
     row= [v1, v2]
     data.append(row)
 
 # 拟合VAR模型
 model=VAR(data)
 model_fit=model.fit()
 
 # 进行预测
 yhat=model_fit.forecast(model_fit.y, steps=1)
 print(yhat)

模型诊断

  • Granger因果检验：确定变量间的因果关系
  • 脉冲响应函数分析：评估一个变量的冲击对其他变量的影响
  • 预测误差方差分解：分析每个变量对预测误差的贡献
  • 模型稳定性检查：确保所有特征根位于单位圆内

VAR模型在多变量时间序列分析中扮演着重要角色，特别是在需要考虑多个相互关联变量的情况下。它提供了一个系统的框架来分析变量之间的动态相互作用，但同时也要求分析者具有丰富的专业知识来正确指定和解释模型。在实际应用中，通常需要结合经济理论、统计诊断和实证分析来选择最佳的模型规格。

8、向量自回归移动平均（VARMA）模型

向量自回归移动平均（VARMA）模型是VAR模型的扩展，它结合了向量自回归（VAR）和向量移动平均（VMA）的特性，用于分析多变量时间序列数据。

数学表示

VARMA(p,q)模型可以表示为：

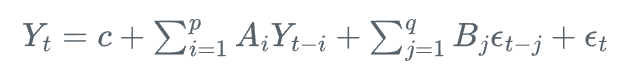
其中，Y_t是k维随机向量，c是k维常数向量，A_i和B_j是k×k系数矩阵，\epsilon_t是k维白噪声向量。

优势

  • 比VAR模型更灵活，可以捕捉更复杂的动态结构
  • 可能比VAR模型更简洁（在某些情况下）
  • 适用于具有移动平均特性的多变量时间序列

局限性

  • 参数估计复杂，可能存在识别问题
  • 计算成本高，特别是对于高维系统
  • 模型选择和诊断更为复杂

适用场景

  • 复杂的经济系统建模
  • 金融市场多资产收益率分析
  • 多变量工业过程控制

参数解释

  • p：自回归阶数
  • q：移动平均阶数
  • 系数矩阵A_i和B_j：分别表示自回归和移动平均部分的影响

Python实现

 fromstatsmodels.tsa.statespace.varmaximportVARMAX
 fromrandomimportrandom
 
 # 生成示例多变量数据
 data=list()
 foriinrange(100):
     v1=random()
     v2=v1+random()
     row= [v1, v2]
     data.append(row)
 
 # 拟合VARMA模型
 model=VARMAX(data, order=(1, 1))
 model_fit=model.fit(disp=False)
 
 # 进行预测
 yhat=model_fit.forecast()
 print(yhat)

模型诊断

  • 多变量Ljung-Box检验：检查残差的白噪声性质
  • 信息准则（如AIC、BIC）用于模型选择
  • 交叉相关函数（CCF）分析：检查变量间的相关性

9、具有外生回归量的向量自回归移动平均（VARMAX）模型

VARMAX模型是VARMA模型的进一步扩展，它允许在模型中包含外生变量。这使得模型能够考虑额外的解释变量对多个相关时间序列的影响。

数学表示

VARMAX(p,q,r)模型可以表示为：

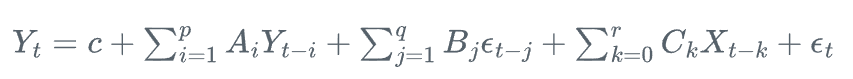
其中，X_t是外生变量向量，C_k是相应的系数矩阵。

优势

  • 可以纳入额外的解释变量，提高预测精度
  • 能够捕捉内生变量和外生变量之间的复杂关系
  • 适用于需要考虑外部因素影响的多变量时间序列分析

局限性

  • 模型复杂度高，可能面临过拟合风险
  • 需要准确预测外生变量才能进行长期预测
  • 参数估计和模型选择更为复杂

适用场景

  • 宏观经济预测（考虑政策变量）
  • 多产品销售预测（考虑营销支出）
  • 金融市场分析（考虑多个经济指标）

参数解释

与VARMA模型相同，额外包括：

  • r：外生变量的滞后阶数
  • 系数矩阵C_k：表示外生变量对内生变量的影响

Python实现

 fromstatsmodels.tsa.statespace.varmaximportVARMAX
 fromrandomimportrandom
 
 # 生成示例多变量数据和外生变量
 data=list()
 exog_data=list()
 foriinrange(100):
     v1=random()
     v2=v1+random()
     data.append([v1, v2])
     exog_data.append([i+random()])
 
 # 拟合VARMAX模型
 model=VARMAX(data, exog=exog_data, order=(1, 1))
 model_fit=model.fit(disp=False)
 
 # 进行预测
 exog_forecast= [[100+random()]]
 yhat=model_fit.forecast(exog=exog_forecast)
 print(yhat)

模型诊断

  • 外生变量的显著性检验
  • 格兰杰因果检验：检查外生变量对内生变量的因果关系
  • 预测性能评估：比较包含和不包含外生变量的模型

10、简单指数平滑（SES）模型

简单指数平滑（SES）是一种基本的时间序列预测方法，它对过去的观测值赋予指数递减的权重。这种方法特别适用于没有明显趋势或季节性的数据。

数学表示

SES模型可以表示为：

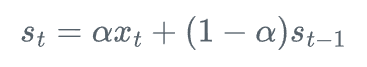
其中，s_t是t时刻的平滑值，x_t是t时刻的实际观测值，\alpha是平滑参数（0 < \alpha < 1）。

优势

  • 计算简单，易于理解和实现
  • 对最近的观测值给予更高的权重
  • 适用于短期预测

局限性

  • 不适用于具有明显趋势或季节性的数据
  • 对初始值的选择敏感
  • 可能无法捕捉复杂的时间序列模式

适用场景

  • 短期需求预测
  • 金融市场短期波动预测
  • 稳定性较高的时间序列预测

参数解释

  • \alpha：平滑参数，控制新观测值的权重

Python实现

 fromstatsmodels.tsa.holtwintersimportSimpleExpSmoothing
 fromrandomimportrandom
 
 # 生成示例数据
 data= [x+random() forxinrange(1, 100)]
 
 # 拟合SES模型
 model=SimpleExpSmoothing(data)
 model_fit=model.fit()
 
 # 进行预测
 yhat=model_fit.predict(len(data), len(data))
 print(yhat)

模型诊断

  • 残差分析：检查残差的随机性和正态性
  • 预测误差评估：使用MAE、MSE等指标
  • 参数稳定性检查：评估不同\alpha值对预测的影响

11、Holt-Winters指数平滑（HWES）模型

Holt-Winters指数平滑（HWES）模型，也称为三重指数平滑，是简单指数平滑的扩展，它可以处理具有趋势和季节性的时间序列数据。

数学表示

加法Holt-Winters模型的方程：

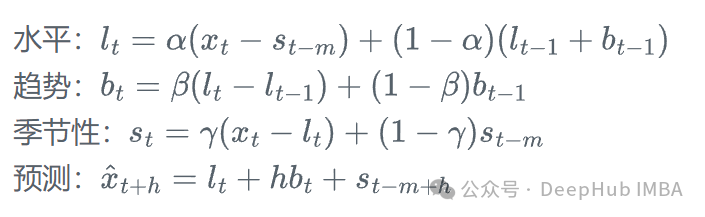
其中，l_t是水平项，b_t是趋势项，s_t是季节性项，m是季节周期，\alpha、\beta和\gamma是平滑参数。

优势

  • 可以处理具有趋势和季节性的数据
  • 对最近的观测值给予更高的权重
  • 适用于中短期预测

局限性

  • 对异常值敏感
  • 可能无法捕捉非线性趋势
  • 需要较长的历史数据来估计季节性成分

适用场景

  • 季节性销售预测
  • 能源需求预测
  • 旅游业客流量预测

参数解释

  • \alpha：水平平滑参数
  • \beta：趋势平滑参数
  • \gamma：季节性平滑参数

Python实现

 fromstatsmodels.tsa.holtwintersimportExponentialSmoothing
 fromrandomimportrandom
 
 # 生成示例数据
 data= [x+10*sin(x/5) +random() forxinrange(1, 100)]
 
 # 拟合Holt-Winters模型
 model=ExponentialSmoothing(data, seasonal_periods=12, trend='add', seasonal='add')
 model_fit=model.fit()
 
 # 进行预测
 yhat=model_fit.predict(len(data), len(data))
 print(yhat)

模型诊断

  • 残差分析：检查残差的随机性、正态性和自相关性
  • 预测误差评估：使用MAE、MAPE等指标
  • 参数稳定性检查：评估不同初始值对预测的影响

模型比较

复杂度递增

  • 最简单：SES < AR/MA < ARMA < ARIMA
  • 中等复杂：SARIMA < SARIMAX
  • 最复杂：VAR < VARMA < VARMAX

单变量 vs 多变量

  • 单变量模型：AR, MA, ARMA, ARIMA, SARIMA, SARIMAX, SES, HWES
  • 多变量模型：VAR, VARMA, VARMAX

处理能力

  • 趋势：ARIMA, SARIMA, SARIMAX, HWES
  • 季节性：SARIMA, SARIMAX, HWES
  • 外生变量：SARIMAX, VARMAX

计算效率

  • 高效：SES, AR, MA
  • 中等：ARMA, ARIMA, VAR
  • 计算密集：SARIMA, SARIMAX, VARMA, VARMAX

预测范围

  • 短期预测：SES, AR, MA, ARMA
  • 中长期预测：ARIMA, SARIMA, VAR, HWES
  • 条件长期预测：SARIMAX, VARMAX（依赖外生变量的准确预测）

如何选择

  1. 数据特征分析：- 平稳性：非平稳数据考虑ARIMA或其变体- 季节性：存在明显季节性模式选择SARIMA或HWES- 多变量关系：考虑VAR系列模型
  2. 预测目标：- 短期预测：可以考虑较简单的模型如AR、MA或SES- 长期预测：ARIMA、SARIMA或VARMAX可能更合适
  3. 计算资源：- 有限资源：优先考虑计算效率高的模型- 充足资源：可以尝试更复杂的模型或集成方法
  4. 解释性需求：- 高解释性要求：线性模型如AR、ARIMA通常更易解释- 性能优先：可以考虑非线性或机器学习方法
  5. 外部因素影响：- 存在已知外部影响因素：考虑SARIMAX或VARMAX
  6. 数据量：- 大数据集：可以考虑更复杂的模型或深度学习方法- 小数据集：简单模型如SES或AR可能更稳定

总结

本文详细介绍了11种经典的时间序列预测方法，从简单的自回归模型到复杂的多变量模型。每种方法都有其特定的应用场景和优缺点，没有一种模型可以适用于所有情况。选择合适的模型需要考虑数据特征、预测目标、可用资源和领域知识。在实践中，通常需要尝试多个模型并比较它们的性能。

时间序列分析是一个广泛而深入的领域，本文仅涵盖了其中的一部分内容。随着机器学习和深度学习技术的发展，如长短期记忆网络（LSTM）和Prophet等新方法也越来越多地应用于时间序列预测。然而，这些经典方法仍然是时间序列分析的基础，对于理解更复杂的方法和选择合适的预测策略至关重要。

在实际应用中，建议尝试多种方法并比较其性能。同时结合领域知识和数据可视化技术，可以帮助更好地理解数据的特性和选择合适的预测方法。

标签： 机器学习 时间序列 python

记录[+]

2024-10-22T09:30:45+08:00 已修改
登录后发布评论

“11种经典时间序列预测方法：理论、Python实现与应用”的评论:

还没有评论
关于作者
...
Deephub
更多文章请关注公众号：Deephub-IMBA
相关阅读

LLM2CLIP：使用大语言模型提升CLIP的文本处理，提高长文本理解和跨语言能力

解读双编码器和交叉编码器：信息检索中的向量表示与语义匹配

使用Pytorch构建视觉语言模型（VLM）

使用 PyTorch-BigGraph 构建和部署大规模图嵌入的完整教程

25 个值得关注的检索增强生成 (RAG) 模型和框架

利用PyTorch的三元组损失Hard Triplet Loss进行嵌入模型微调

告别Print，使用IceCream进行高效的Python调试

文章导航