【数据结构】用堆排序解决TOPK问题

题目名称 TOPK问题

目录

推荐阅读顺序:

1.题目->3.答案->2.题目分析->4.题目知识点

1.题目

给定一个文件，找出文件中前K个数字，最后打印在屏幕上。

void PrintTopK(const char* filename, int k)
{

}

2.题目分析

找前K个最大的？如何处理？

1.使用堆排序 O(N*logN)

2.堆选数。

a.建大堆——————————————————

   相当于选K次即可，如果有数据结构堆就相当于popK次，没有数据结构，就类比于选出最大的数在堆顶然后以此和最后一个元素互换，再向下调整，这样做K次就好，效率为O(N+logN*K)。

    这样做有一个bug，假设N很大，K很小，比如N=100亿 K=100，那么a方法就不行了。

    因为堆必须在内存上申请空间，在N很大的时候，数据在内存上就存储不下了，只能存储在磁盘中。(补充一下:**1GB约等于10亿字节**）。

b.建小堆——————————————————

    用前K个数，建K个数的小堆。K+logK*(N-K) 时间复杂度为O(N)空间复杂度为O(K)

    依次遍历后面N-K个数，如果比堆顶数据大，就替换堆顶数据，向下调整进堆。最后堆里面的数据就是最大的前K个。

3.题目答案

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
void swap(int* x, int* y)
{
    int z = 0;
    z = *x;
    *x = *y;
    *y = z;
}

void AdjustDown(int *minHeap,int size,int parent)
{
    int minchild = parent * 2 + 1;
    while (minchild < size)
    {
        if((minchild+1)<size && (minHeap[minchild] > minHeap[minchild + 1]))
        {
            minchild++;
        }
        if (minHeap[parent] > minHeap[minchild])
        {
            swap(&minHeap[parent], &minHeap[minchild]);
            parent = minchild;
            minchild = parent * 2 + 1;
        }
        else
        {
            break;
        }
    }
    
}

void PrintTopK(const char* filename, int k)
{
    assert(filename);

    FILE* fp = fopen(filename, "r");
    if (fp == NULL)
    {
        perror("file error\n");
        exit(-1);
    }

    int * minHeap = (int*)malloc(sizeof(int) * k);
    if (fp == NULL)
    {
        perror("file error\n");
        exit(-1);
    }

    for (int i = 0; i < k; i++)
    {
        fscanf(fp, "%d", &minHeap[i]);
    }

    for (int parent = (k - 1 - 1) / 2; parent >= 0; parent--)
    {
        AdjustDown(minHeap,k, parent);
    }

    int tmp = 0;
    while (fscanf(fp, "%d", &tmp) != EOF)
    {
        if (tmp > minHeap[0])
        {
            swap(&tmp, &minHeap[0]);
            AdjustDown(minHeap, k, 0);
        }
    }
    
    for (int i = 0; i < k; i++)
    {
        printf("%d ", minHeap[i]);
    }
    printf("\n");

    //不要忘记free
    free(minHeap);
    fclose(fp);
}

int main()
{
    const char* filename = "D:\\CLASS CODE\\LeetCode\\leet-code-exercise\\力扣练习\\topkdata.txt";
    int N = 10000;
    int K = 5;
    //CreateDataFile(filename, N);
    PrintTopK(filename, K);

    return 0;
}

4.题目知识点

4.1TOPK

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。 比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。 对于Top-K问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太可取了(可能数据都不能一下子全部加载到内存中，1GB差不多10亿字节)。

最佳的方式就是用堆来解决，基本思路如下：

1. 用数据集合中前K个元素来建堆，前k个最大的元素，则建小堆， 前k个最小的元素，则建大堆。

2. 用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素将剩余N-K个元素依次与堆顶元素比完之后，堆中剩余的K个元素就是所求的前K个最小或者最大的元素。

4.2堆排序详解

简单介绍一下堆排序

堆排序本质是一种选择排序，找到最大的元素之后要考虑如何选次小的元素。

堆排序时要利用堆排序本身的优势，它的父子节点的关系。

如果想看堆排序详解可以移步我的这篇博文：

(8条消息) 【数据结构】堆排序的实现_vpurple__的博客-CSDN博客https://blog.csdn.net/vpurple_/article/details/126233090?spm=1001.2014.3001.5501

4.3代码分析

向下调整函数：

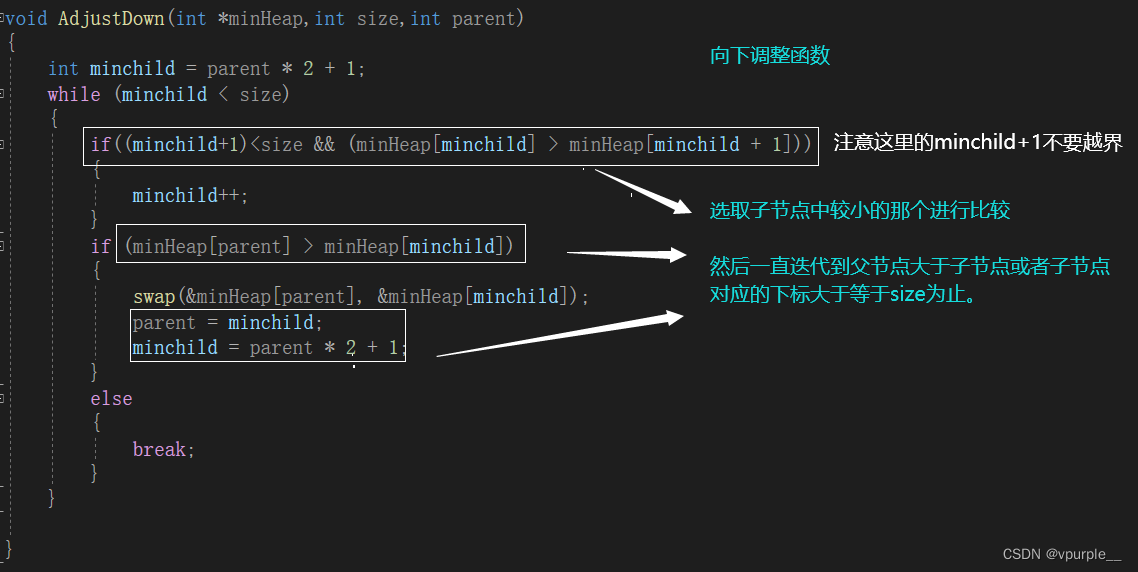
打印TOPK函数：

大家好这里是媛仔，欢迎来到媛仔的题目分享栏目，希望篇文章对你能够有所帮助~也希望大家可以找我多多交流，我们下期再见！！