文章目录
前言
近些年图神经网络十分火热,因为图数据结构其实在我们的现实生活中更常见,例如分子结构、人的社交关系、语言结构等等。NLP中的句法树、依存树就是一种特殊的图,因此,图神经网络的学习也是必不可少的。
GCN
GCN是图卷积神经网络,初期研究者为了从数学上严谨的推导该公式是有效的,所以会涉及到诸如傅里叶变换,拉普拉斯算子的知识,但是对于我们使用者而言,并不需要会证明GCN最终能收敛等等知识,能够懂大概原理和计算方式就差不多了吧…
下面介绍GCN原文中的一些关键点。
传播公式
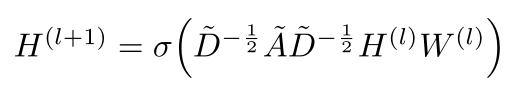
其中
H(l) 是值输入的特征
H(l+1) 是指更新后输出的新的特征
σ()为激活函数(可以是RELU等)
A
~
\widetilde{A}
A 为有自连的邻接矩阵(A为邻接矩阵,I为单位矩阵(单位矩阵对角线为1),则
A
~
\widetilde{A}
A = A + I)
D
~
\widetilde{D}
D 为自连矩阵的度矩阵,因为度矩阵除对角线上元素都为0,那么他的-1/2次方就是对角线元素取根号分之一的矩阵。
理论和实际总是会有差距,就像讲到这里肯定还是一脸懵,不知道该这么计算,那么浅浅举个例子应该就知道了。
例1
假设有这么一张图,应该怎么更新节点1的特征呢?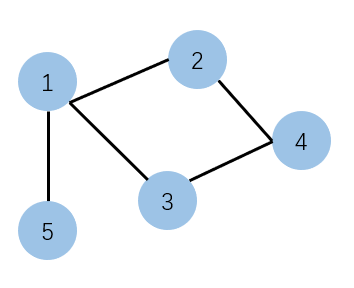
(直接上手好了)
首先图的邻接矩阵A如下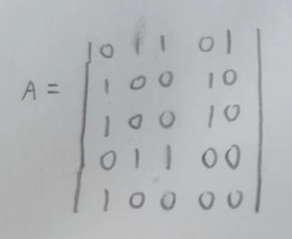
自相连矩阵
A
~
\widetilde{A}
A就是加上对角线元素,因为更新特征的时候也要考虑自己的特征,如下:
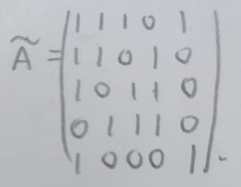
D
~
\widetilde{D}
D自连矩阵的度矩阵,就是每个对角线是对应的度,如下:
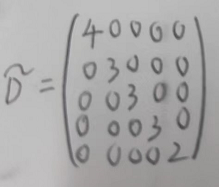
因为除对角线元素外都是0,那么他的负二分之一次方就是对每个元素开根号分之一,即可: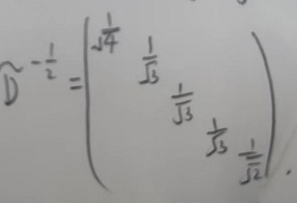
那么以节点1为例的特征更新就可以表示如下: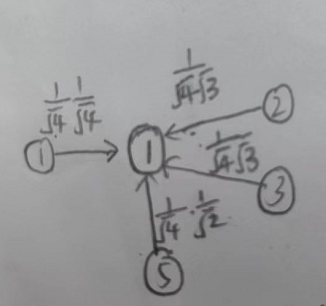
使用1、2、3、5的节点特征来更新1节点的特征,可以看到分母左边的乘数就是1节点的度的开根号,这种操作像不像归一化的操作,因此这样的计算公式也是有道理可循的。
1、2、3、5边上的数值就是此节点特征对应的权重,特征*权重之后传播给节点1更新特征,可以将他们求和然后经过激活函数即可完成更新。那么GCN如何传播以及参数更新应该就有一个比较形象的理解了,每个节点的特征都会包含一定的邻居的特征。我猜想可能GCN迭代次数多了节点特征趋于同质化的问题可能就源于此吧。
例2
例1是b站上视频看来的,感觉能够对传播公式有比较深刻的理解,因此记录下来。我们也可以看看原论文中讲的例子。
例如有两层GCN,那么他是如何传播更新呢?
经过例1应该可以比较简单理解这个公式了,这里:
A
^
\widehat{A}
A就是一个输入的常量,可以看成每个节点对应的一个权重矩阵,就是用于消息传播中挑选哪些特征来更新此节点特征的。
X就是输入的此节点的特征
W(0) 就是GCN的第一层参数,需要学习的参数
W(1) 就是GCN的第二层参数,需要学习的参数
ReLU(
A
~
\widetilde{A}
AXW(0))其实就是之前的更新参数的公式,那么这个结果就是第一层GCN后得到的此节点的特征,那么再经过第二层GCN更新之后就是两层GCN网络得到的此节点的特征了。
只不过第二次的激活函数和第一次的激活函数有所区别,第一层是ReLU,第二层是用softmax,其对应的定义如下: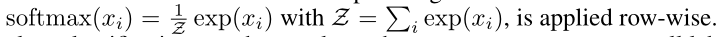
因为论文中是对应多分类任务,因此损失函数使用交叉熵函数如下: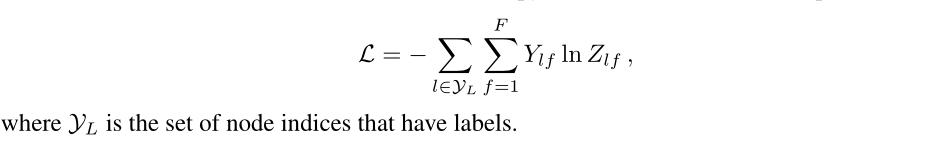
DGL中的GCN实例
dgl.DGLGraph.update_all
关于dgl图的一些基本操作可以参考:DGL的图数据结构的创建、图的特征、dgl.batch及一些理解
基于此,这里将先重点介绍一下dgl.DGLGraph.update_all的操作,理解了这个的作用,dlg的GCN代码就会变的比较简单了。
首先,我们先建立这么一张图:
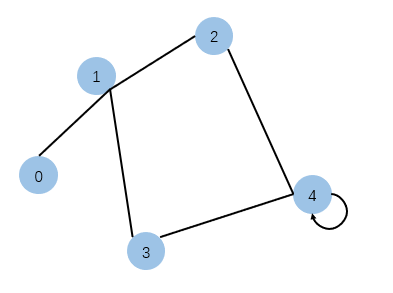
图是无向图,不仅如此,节点4能够自连。
那么直接上代码看结果就知道信号是怎么传播的了。
import dgl
import dgl.function as fn
import torch
# 构建图
g = dgl.graph(([0,1,1,1,2,3,2,4,3,4,4],[1,0,3,2,1,1,4,2,4,3,4]))# 每个节点的特征都为[1, 1]
g.ndata['x']= torch.ones(5,2)# 节点4的特征为[0.2, 0.5]
g.ndata['x'][4]= torch.tensor([0.2,0.5])# 消息汇聚更新
g.update_all(fn.copy_u(u='x', out='m'), fn.sum(msg='m', out='h'))print(g.ndata['x'])print(g.ndata['h'])
运行结果如下:
tensor([[1.0000, 1.0000],
[1.0000, 1.0000],
[1.0000, 1.0000],
[1.0000, 1.0000],
[0.2000, 0.5000]])
tensor([[1.0000, 1.0000],
[3.0000, 3.0000],
[1.2000, 1.5000],
[1.2000, 1.5000],
[2.2000, 2.5000]])
其中输出的第一个tensor是每个节点的特征
第二个tensor是进行依次消息传播后,保存在h中的更新后的消息
那么
g.update_all(fn.copy_u(u='x', out='m'), fn.sum(msg='m', out='h'))
该怎么理解呢
fn.copy_u(u='x', out='m')
这个可以理解为,拷贝一份邻居节点的“x“的特征,然后存储在“m”中,但是由于是中间变量,并不会保存在ndata中的。
fn.sum(msg='m', out='h')
这个可以理解为,使用”m“特征,对其进行对应维度求和的操作,然后得出”h“特征并且将其赋值给ndata[“h”]
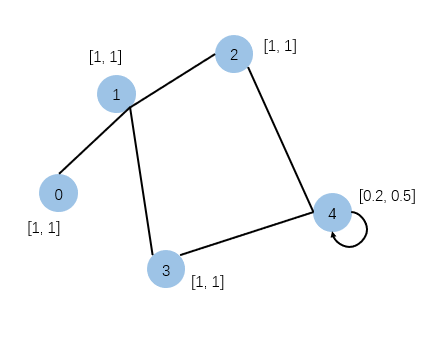
tensor([[1.0000,1.0000],[3.0000,3.0000],[1.2000,1.5000],[1.2000,1.5000],[2.2000,2.5000]])
那么再回过头来原来的图和输出的结果,可以发现他好像就是GCN的传播方式,只不过少了每个邻居节点的权重而已。
那么我们现在来看DGL官网提供的GCN代码就比较简单易懂了
首先版本号需要对上:
dgl == 0.6.1
torch == 1.9.1
否则可以会因为dgl和torch版本不匹配而报错。
我注释好的代码如下:
import dgl
import dgl.function as fn
import torch as th
import torch.nn as nn
import torch.nn.functional as F
from dgl import DGLGraph
# 定义消息传播更新的方式————————————————————————————————————# 把一个有向边的源节点的信息复到自己(目标节点)的的信息邮箱里,# 相当于放到一个中转站,缓冲区里,所以等下我们需要汇总,一并处理
gcn_msg = fn.copy_u(u='h', out='m')# 把邮箱中的信息进行聚合(这里是求和),并保存在节点的某一个特征里。
gcn_reduce = fn.sum(msg='m', out='h')# 定义GCNLayer——————————————————————————————————————————————————classGCNLayer(nn.Module):def__init__(self, in_feats, out_feats):super(GCNLayer, self).__init__()
self.linear = nn.Linear(in_feats, out_feats)defforward(self, g, feature):# 使用local_scope() 范围时,任何对节点或边的修改在脱离这个局部范围后将不会影响图中的原始特征值 。# 真白点就是:在这个范围中,你可以引用、修改图中的特征值 ,但是只是临时的,出了这个范围,一切恢复原样。# 这样做的目的是方便计算。毕竟我们在图上作消息传递和聚合,有时仅是为了计算值 并不想改变原始图。with g.local_scope():# h存储每个节点的特征值
g.ndata['h']= feature
# GCN邻居传播求和更新参数
g.update_all(gcn_msg, gcn_reduce)# 获取传播后的结果
h = g.ndata['h']# 经过线性层(公式中的W)return self.linear(h)# 定义两层GCN模型——————————————————————————————————classNet(nn.Module):def__init__(self):super(Net, self).__init__()
self.layer1 = GCNLayer(1433,16)
self.layer2 = GCNLayer(16,7)defforward(self, g, features):# 第一层激活函数为relu
x = F.relu(self.layer1(g, features))
x = self.layer2(g, x)return x
net = Net()print(net)# 定义获取自带数据集函数——————————————————————————————————————————————————from dgl.data import CoraGraphDataset
defload_cora_data():
dataset = CoraGraphDataset()print(dataset)# 这个数据集中只有一个图,因此不用自己分batch
g = dataset[0]# 每个节点的特征值
features = g.ndata['feat']# 每个节点的标签
labels = g.ndata['label']# 用于区分参与训练的节点
train_mask = g.ndata['train_mask']# 用于区分参与测试的节点
test_mask = g.ndata['test_mask']return g, features, labels, train_mask, test_mask
# 定义评价模型的函数————————————————————————————————————————————defevaluate(model, g, features, labels, mask):
model.eval()with th.no_grad():
logits = model(g, features)
logits = logits[mask]
labels = labels[mask]
_, indices = th.max(logits, dim=1)
correct = th.sum(indices == labels)return correct.item()*1.0/len(labels)# 模型训练———————————————————————————————————————————————————————————————import time
import numpy as np
g, features, labels, train_mask, test_mask = load_cora_data()# GCN需要考虑自己的特征,因此需要自连
g.add_edges(g.nodes(), g.nodes())
optimizer = th.optim.Adam(net.parameters(), lr=1e-2)
dur =[]for epoch inrange(50):if epoch >=3:
t0 = time.time()
net.train()
logits = net(g, features)
logp = F.log_softmax(logits,1)
loss = F.nll_loss(logp[train_mask], labels[train_mask])
optimizer.zero_grad()
loss.backward()
optimizer.step()if epoch >=3:
dur.append(time.time()- t0)
acc = evaluate(net, g, features, labels, test_mask)print("Epoch {:05d} | Loss {:.4f} | Test Acc {:.4f} | Time(s) {:.4f}".format(
epoch, loss.item(), acc, np.mean(dur)))
但是如果还记得GCN原文中的公式的话,会发现代码可能有点问题,因为原文中不是有个邻居权重的吗,那个
D
~
\widetilde{D}
D什么的计算去哪了,好像在代码里没看到权重计算的东西,好像这里就是单纯的求和。
我也盯着代码找了一会,这个权重好像确实没出现啊,然后我在官网继续往下看了看
大概的意思就是说这个例子他把权重去了,就是简单求和了
哦,那没事了,这就是简单版的GCN。
完整版的在这里
参考
SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS
合集【图神经网络基础】( 代码DGL版 )
版权归原作者 Icy Hunter 所有, 如有侵权,请联系我们删除。