文章目录
1.1 全连接前馈神经网络
前馈神经网络（Feedforward Neural Network,FNN）也称为多层感知器（实际上前馈神经网络由多层Logistic回归模型组成）
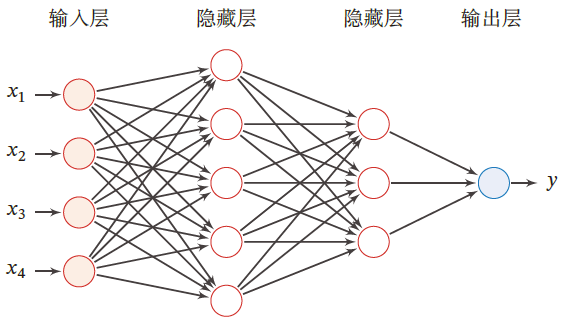
前馈神经网络中，各个神经元属于不同的层
每层神经元接收前一层神经元的信号，并输出到下一层
- 输入层：第0层
- 输出层：最后一层
- 隐藏层：其他中间层
整个网络中无反馈，信号从输入层向输出层单向传播，可用一个有向无环图表示
1.1.1 符号说明
超参数
符号含义
L
L
L神经网络层数
M
l
M_l
Ml第
l
l
l 层神经元个数
f
l
(
⋅
)
f_l(\cdot)
fl(⋅)第
l
l
l 层神经元的激活函数
参数
符号含义
W
(
l
)
∈
R
M
l
×
M
l
−
1
W^{(l)}\in \R^{M_l\times M_{l-1}}
W(l)∈RMl×Ml−1第
l
−
1
l-1
l−1 层到第
l
l
l 层的权重矩阵
b
(
l
)
∈
R
M
l
×
M
l
−
1
b^{(l)}\in \R^{M_l\times M_{l-1}}
b(l)∈RMl×Ml−1第
l
−
1
l-1
l−1 层到第
l
l
l 层的偏置
活性值
符号含义
z
(
l
)
∈
R
M
l
z^{(l)}\in\R^{M_l}
z(l)∈RMl第
l
l
l 层神经元的净输入（净活性值）
a
(
l
)
∈
R
M
l
a^{(l)}\in \R^{M_{l}}
a(l)∈RMl第
l
l
l 层神经元的输出（活性值）
1.1.2 信息传播公式
神经网络的第
l
l
l 层有
M
l
M_l
Ml 个神经元，相应的有
M
l
M_l
Ml 个净输入和活性值，所以二者需要由
R
M
l
\R^{M_l}
RMl 向量来表示
第
l
l
l 层的输入为第
l
−
1
l-1
l−1 层的活性值，相应的为
R
M
l
−
1
\R^{M_{l-1}}
RMl−1 向量，即
z
(
l
−
1
)
,
a
(
l
−
1
)
∈
R
M
l
−
1
z^{(l-1)},a^{(l-1)}\in \R^{M_{l-1}}
z(l−1),a(l−1)∈RMl−1
故第
l
l
l 层神经元的净输入需要经过一个 **仿射变换**，即
z
(
l
)
=
W
(
l
)
a
(
l
−
1
)
+
b
(
l
)
，其中
W
(
l
)
∈
R
M
l
×
M
l
−
1
=
W
(
l
−
1
)
f
l
−
1
(
z
(
l
−
1
)
)
+
b
(
l
)
\begin{aligned} z^{(l)}&=W^{(l)}a^{(l-1)}+b^{(l)}，其中 W^{(l)}\in \R^{M_l\times M_{l-1}}\\ &=W^{(l-1)}f_{l-1}(z^{(l-1)})+b^{(l)} \end{aligned}
z(l)=W(l)a(l−1)+b(l)，其中W(l)∈RMl×Ml−1=W(l−1)fl−1(z(l−1))+b(l)
活性值
a
(
l
)
a^{(l)}
a(l) 需要经过一个 **非线性变换**
a
(
l
)
=
f
l
(
z
(
l
)
)
=
f
l
(
W
(
l
)
a
(
l
−
1
)
+
b
(
l
)
)
\begin{aligned} a^{(l)}&=f_l(z^{(l)})\\ &=f_l(W^{(l)}a^{(l-1)}+b^{(l)}) \end{aligned}
a(l)=fl(z(l))=fl(W(l)a(l−1)+b(l))
进而可知，由输入到网络最后的输出
a
(
L
)
a^{(L)}
a(L)
x
=
a
(
0
)
→
W
1
z
(
1
)
→
f
1
(
)
a
(
1
)
⋯
→
f
L
−
1
(
)
a
(
L
−
1
)
→
W
L
z
(
L
)
→
f
L
(
)
a
(
L
)
=
ϕ
(
x
;
W
;
b
)
x=a^{(0)}\xrightarrow{W_1}z^{(1)}\xrightarrow{f_1()}a^{(1)}\cdots\xrightarrow{f_{L-1}()}a^{(L-1)}\xrightarrow{W_{L}}z^{(L)}\xrightarrow{f_L()}a^{(L)}=\phi(x;W;b)
x=a(0)W1z(1)f1()a(1)⋯fL−1()a(L−1)WLz(L)fL()a(L)=ϕ(x;W;b)
其中
W
,
b
W,b
W,b 表示网络中所有层的连接权重和偏置
前馈神经网络可以通过逐层的信息传递，整个网络可以看做一个复合函数
ϕ
(
x
;
W
;
b
)
\phi(x;W;b)
ϕ(x;W;b)
通用近似定理
根据通用近似定理，对于具有 线性输出层
z
(
l
)
z^{(l)}
z(l) 和至少一个 **具有挤压性质的激活函数**
ϕ
(
⋅
)
\phi(\cdot)
ϕ(⋅) 的隐藏层组成的前馈神经网络，只要隐藏层的神经元数量足够，就可以以任意精度来近似任何一个定义在实数空间中的有界闭函数
1.1.3 神经网络与机器学习结合
神经网络可以作为一个万能函数，用于进行复杂的特征转换或逼近一个条件分布
在机器学习中，输入样本的特征对分类器性能的影响很大
若要获得很好的分类效果，需要将样本的原始特征向量
x
x
x 转换到更有效的特征向量
ϕ
(
x
)
\phi(x)
ϕ(x) ——特征抽取
多层前馈神经网络恰好可以看做一个非线性函数
ϕ
(
⋅
)
\phi(\cdot)
ϕ(⋅) ，将输入
x
∈
R
D
x\in \R^D
x∈RD 映射到输出
ϕ
(
x
)
∈
R
D
′
\phi(x)\in \R^{D'}
ϕ(x)∈RD′ ，因此可将多层前馈神经网络看作一种特殊的特征转换方法，其输出
ϕ
(
x
)
\phi(x)
ϕ(x) 作为分类器的输入
y
^
=
g
(
ϕ
(
x
)
;
θ
)
\hat{y}=g(\phi(x);\theta)
y^=g(ϕ(x);θ)
g ( ⋅ ) g(\cdot) g(⋅) 为线性或非线性分类器θ \theta θ 为分类器 g ( ⋅ ) g(\cdot) g(⋅) 的参数y ^ \hat{y} y^ 为分类器输出
若分类器
g
(
⋅
)
g(\cdot)
g(⋅) 为
L
o
g
i
s
t
i
c
回归
Logistic回归
Logistic回归 或
S
o
f
t
m
a
x
回归
Softmax回归
Softmax回归 ，则相当于在输出层引入分类器，神经网络直接输出在不同类别的条件概率
p
(
y
∣
x
)
p(y\vert x)
p(y∣x)
二分类问题
对于二分类问题
y
∈
{
0
,
1
}
y\in \{0,1\}
y∈{0,1} ，且采用
L
o
g
i
s
t
i
c
回归
Logistic回归
Logistic回归 ，那么
L
o
g
i
s
t
i
c
Logistic
Logistic 相当与神经网络的输出层，只需要一个神经元，其激活函数就是
L
o
g
i
s
t
i
c
函数
Logistic函数
Logistic函数 ，可直接作为类别
y
=
1
y=1
y=1 的条件概率
p
(
y
=
1
∣
x
)
=
a
(
L
)
∈
R
p(y=1\vert x)=a^{(L)}\in \R
p(y=1∣x)=a(L)∈R
多分类问题
对于多分类问题
y
∈
{
1
,
⋯
,
C
}
y\in \{1,\cdots,C\}
y∈{1,⋯,C} ，如果使用
S
o
f
t
m
a
x
回归
Softmax回归
Softmax回归 ，相当于网络最后一层设置
C
C
C 个神经元，其激活函数为
S
o
f
t
m
a
x
函数
Softmax函数
Softmax函数 ，网络最后一层的输出可以作为每个类的条件概率
y
^
=
s
o
f
t
m
a
x
(
z
(
l
)
)
\hat{y}=softmax(z^{(l)})
y^=softmax(z(l))
其中，
z
(
L
)
∈
R
C
z^{(L)}\in \R^C
z(L)∈RC 为第
L
L
L 层神经元的净输入
y
^
∈
R
C
\hat{y}\in\R^C
y^∈RC 为第
L
L
L 层神经元的活性值，每一维分别表示不同类别标签的预测条件概率
1.1.4 参数学习
如果采用交叉熵损失函数，对于样本
(
x
,
y
)
(x,y)
(x,y) ，其损失函数为
L
(
y
,
y
^
)
=
−
y
log
y
^
,
y
∈
{
0
,
1
}
C
\mathcal{L}(y,\hat{y})=-y\log \hat{y},y\in \{0,1\}^C
L(y,y^)=−ylogy^,y∈{0,1}C
给定训练集
D
=
{
(
x
i
,
y
i
)
}
i
=
1
N
\mathcal{D}=\{(x_i,y_i)\}_{i=1}^N
D={(xi,yi)}i=1N ，将每个样本
x
i
x_i
xi 输入给前馈网络得到
y
^
i
\hat{y}_i
y^i ，其结构化风险函数为
R
(
W
,
b
)
=
1
N
∑
i
=
1
N
L
(
y
i
,
y
^
i
)
+
1
2
λ
∥
W
∥
F
2
\mathcal{R}(W,b)=\frac{1}{N}\sum\limits_{i=1}^N\mathcal{L}(y_i,\hat{y}_i)+\frac{1}{2}\lambda\Vert W\Vert_F^2
R(W,b)=N1i=1∑NL(yi,y^i)+21λ∥W∥F2
λ \lambda λ 为超参数， λ \lambda λ 越大， W W W 越接近于0- 一般用 F r o b e n i u s Frobenius Frobenius 范数（F范数）作为惩罚项 ∥ W ∥ F 2 = ∑ l = 1 L ∑ i = 1 M l ∑ j = 1 M l − 1 ( ω i j ( l ) ) 2 \Vert W\Vert_F^2=\sum\limits_{l=1}^L\sum\limits_{i=1}^{M_l}\sum\limits_{j=1}^{M_{l-1}}\left(\omega_{ij}^{(l)}\right)^2 ∥W∥F2=l=1∑Li=1∑Mlj=1∑Ml−1(ωij(l))2
对于网络参数，可以通过梯度下降的方法学习
W
(
l
)
←
W
(
l
)
−
α
∂
R
(
W
,
b
)
∂
W
(
l
)
←
W
(
l
)
−
α
(
1
N
∑
i
=
1
N
∂
L
(
y
i
,
y
^
i
)
∂
W
(
l
)
+
λ
W
(
l
)
)
b
(
l
)
←
b
(
l
)
−
α
∂
R
(
W
,
b
)
∂
b
(
l
)
←
b
(
l
)
−
α
(
1
N
∑
i
=
1
N
∂
L
(
y
i
,
y
^
i
)
∂
b
(
l
)
)
\begin{aligned} W^{(l)}&\leftarrow W^{(l)}-\alpha\frac{\partial \mathcal{R}(W,b)}{\partial W^{(l)}}\\ &\leftarrow W^{(l)}-\alpha\left(\frac{1}{N}\sum\limits_{i=1}^N\frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial W^{(l)}}+\lambda W^{(l)}\right)\\ b^{(l)}&\leftarrow b^{(l)}-\alpha\frac{\partial \mathcal{R}(W,b)}{\partial b^{(l)}}\\ &\leftarrow b^{(l)}-\alpha\left(\frac{1}{N}\sum\limits_{i=1}^N\frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial b^{(l)}}\right) \end{aligned}
W(l)b(l)←W(l)−α∂W(l)∂R(W,b)←W(l)−α(N1i=1∑N∂W(l)∂L(yi,y^i)+λW(l))←b(l)−α∂b(l)∂R(W,b)←b(l)−α(N1i=1∑N∂b(l)∂L(yi,y^i))
矩阵求导
根据求导的自变量和因变量是标量，
列向量
列向量
列向量 还是矩阵 ，我们有9种可能的矩阵求导定义：
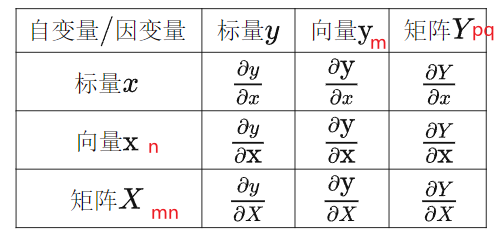
含标量情况：
∂ 标量 ∂ 标量 = 标量 \frac{\partial 标量}{\partial 标量}=标量 ∂标量∂标量=标量∂ 标量 ∂ 向量 = 向量 \frac{\partial 标量}{\partial 向量}=向量 ∂向量∂标量=向量 ， ∂ 标量 ∂ 矩阵 = 矩阵 \frac{\partial 标量}{\partial 矩阵}=矩阵 ∂矩阵∂标量=矩阵∂ 向量 ∂ 标量 = 向量 \frac{\partial 向量}{\partial 标量}=向量 ∂标量∂向量=向量 ， ∂ 矩阵 ∂ 标量 = 矩阵 \frac{\partial 矩阵}{\partial 标量}=矩阵 ∂标量∂矩阵=矩阵
标量情况，第2种和第3种情况，引出信息的两种布局方式
- 分子布局：结果的行维度与分子行维度相同
- 分母布局：结果的行维度与分母行维度相同
不论是向量也好，矩阵也好，对向量求导也好，对矩阵求导也好，结果都可以转化成标量之间的求导，最后把结果按照一定的方式拼接起来，以向量或者矩阵的形式表达出来。
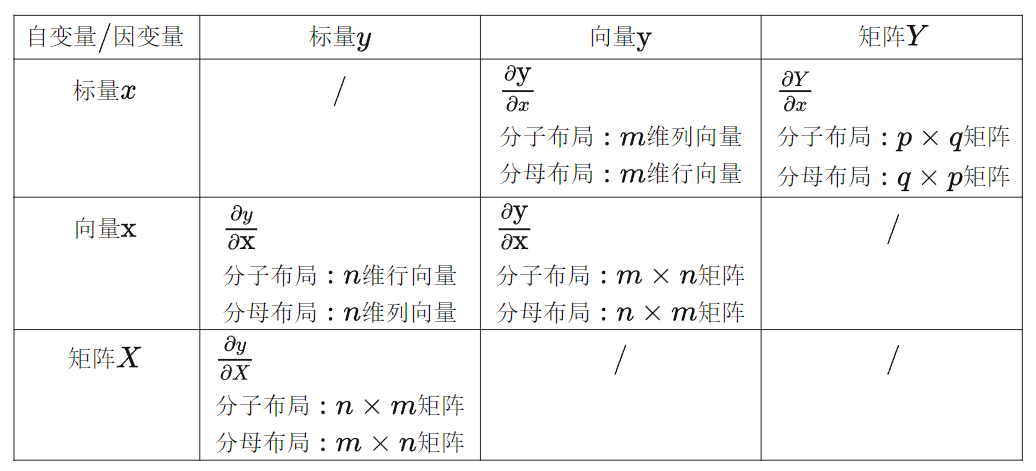
分子布局和分母布局的结果相差一个转置
在机器学习的算法推导中，通常遵循以下布局规则：
- 如果向量或矩阵对标量求导，则以分子布局为主
- 如果标量对向量或矩阵求导，则以分母布局为主
- 向量对向量求导，有些分歧，一般以分子布局的雅克比矩阵为主。
本文沿用nndl的思路，以分母布局为主
若
x
(
i
)
∈
R
x^{(i)}\in \R
x(i)∈R ，向量
x
=
[
x
(
1
)
x
(
2
)
⋮
x
(
M
)
]
∈
R
M
×
1
x=\left[\begin{matrix}x^{(1)}\\x^{(2)}\\\vdots\\x^{(M)}\end{matrix}\right]\in \R^{M\times 1}
x=x(1)x(2)⋮x(M)∈RM×1
- 若 y = g ( x ) ∈ R 1 × 1 y=g(x)\in\R^{1\times 1} y=g(x)∈R1×1 ，则 ∂ y ∂ x = [ ∂ y ∂ x ( 1 ) ∂ y ∂ x ( 2 ) ⋮ ∂ y ∂ x ( M ) ] ∈ R M × 1 \frac{\partial y}{\partial x}=\left[\begin{matrix} \frac{\partial y}{\partial x^{(1)}}\ \frac{\partial y}{\partial x^{(2)}}\ \vdots\ \frac{\partial y}{\partial x^{(M)}} \end{matrix} \right]\in \R^{M\times 1} ∂x∂y=∂x(1)∂y∂x(2)∂y⋮∂x(M)∂y∈RM×1
- 若 y i = g i ( x ) y_i=g_i(x) yi=gi(x) ， y = [ y 1 y 2 ⋮ y N ] ∈ R N × 1 y=\left[\begin{matrix}y_1\y_2\\vdots\y_N\end{matrix}\right]\in \R^{N\times 1} y=y1y2⋮yN∈RN×1 ，则 ∂ y ∂ x = [ ∂ y 1 ∂ x , ∂ y 2 ∂ x , ⋯ , ∂ y N ∂ x ] = [ ∂ y 1 ∂ x 1 ∂ y 2 ∂ x 1 ⋯ ∂ y N ∂ x 1 ∂ y 1 ∂ x 2 ∂ y 2 ∂ x 2 ⋯ ∂ y N ∂ x 2 ⋮ ⋮ ⋱ ⋮ ∂ y 1 ∂ x M ∂ y 2 ∂ x M ⋯ ∂ y N ∂ x M ] ∈ R M × N \frac{\partial y}{\partial x}=\left[ \begin{matrix} \frac{\partial y_1}{\partial x},\frac{\partial y_2}{\partial x},\cdots,\frac{\partial y_N}{\partial x} \end{matrix} \right]=\left[ \begin{matrix} \frac{\partial y_1}{\partial x_1}&\frac{\partial y_2}{\partial x_1}&\cdots&\frac{\partial y_N}{\partial x_1}\ \frac{\partial y_1}{\partial x_2}&\frac{\partial y_2}{\partial x_2}&\cdots&\frac{\partial y_N}{\partial x_2}\ \vdots&\vdots&\ddots&\vdots\ \frac{\partial y_1}{\partial x_M}&\frac{\partial y_2}{\partial x_M}&\cdots&\frac{\partial y_N}{\partial x_M}\ \end{matrix} \right]\in \R^{M\times N} ∂x∂y=[∂x∂y1,∂x∂y2,⋯,∂x∂yN]=∂x1∂y1∂x2∂y1⋮∂xM∂y1∂x1∂y2∂x2∂y2⋮∂xM∂y2⋯⋯⋱⋯∂x1∂yN∂x2∂yN⋮∂xM∂yN∈RM×N
链式法则
y
=
f
5
(
f
4
(
f
3
(
f
2
(
f
1
(
x
)
)
)
)
)
→
∂
y
∂
x
=
∂
f
5
∂
f
4
∂
f
4
∂
f
3
∂
f
3
∂
f
2
∂
f
2
∂
f
1
∂
f
1
∂
x
y=f_5(f_4(f_3(f_2(f_1(x)))))\rightarrow \frac{\partial y}{\partial x}=\frac{\partial f_5}{\partial f_4}\frac{\partial f_4}{\partial f_3}\frac{\partial f_3}{\partial f_2}\frac{\partial f_2}{\partial f_1}\frac{\partial f_1}{\partial x}
y=f5(f4(f3(f2(f1(x)))))→∂x∂y=∂f4∂f5∂f3∂f4∂f2∂f3∂f1∂f2∂x∂f1
若
x
∈
R
x\in \R
x∈R，
{
y
i
=
g
i
(
x
)
y
=
[
g
1
(
x
)
,
g
2
(
x
)
,
⋯
,
g
M
(
x
)
]
∈
R
M
z
i
=
f
i
(
y
)
z
=
[
f
1
(
y
)
,
f
2
(
y
)
,
⋯
,
f
N
(
y
)
]
∈
R
N
\begin{cases} y_i=g_i(x)&y=[g_1(x),g_2(x),\cdots,g_M(x)]\in \R^{M}\\ z_i=f_i(y)&z=\left[f_1(y),f_2(y),\cdots,f_N(y)\right]\in \R^{N} \end{cases}
{yi=gi(x)zi=fi(y)y=[g1(x),g2(x),⋯,gM(x)]∈RMz=[f1(y),f2(y),⋯,fN(y)]∈RN
则有
∂
z
∂
x
=
∂
y
∂
x
1
×
M
∂
z
∂
y
M
×
N
∈
R
1
×
N
\frac{\partial z}{\partial x}=\frac{\partial y}{\partial x}_{1\times M}\frac{\partial z}{\partial y}_{M\times N}\in\R^{1\times N}
∂x∂z=∂x∂y1×M∂y∂zM×N∈R1×N
若
x
∈
R
M
x\in \R^{M}
x∈RM
{
y
i
=
g
i
(
x
)
y
=
[
g
1
(
x
)
,
g
2
(
x
)
,
⋯
,
g
K
(
x
)
]
∈
R
K
z
i
=
f
i
(
y
)
z
=
[
f
1
(
y
)
,
f
2
(
y
)
,
⋯
,
f
N
(
y
)
]
∈
R
N
\begin{cases} y_i=g_i(x)&y=[g_1(x),g_2(x),\cdots,g_K(x)]\in \R^{K}\\ z_i=f_i(y)&z=\left[f_1(y),f_2(y),\cdots,f_N(y)\right]\in \R^{N} \end{cases}
{yi=gi(x)zi=fi(y)y=[g1(x),g2(x),⋯,gK(x)]∈RKz=[f1(y),f2(y),⋯,fN(y)]∈RN
则有
∂
z
∂
x
=
∂
y
∂
x
M
×
K
∂
z
∂
y
K
×
N
∈
R
M
×
N
\frac{\partial z}{\partial x}=\frac{\partial y}{\partial x}_{M\times K}\frac{\partial z}{\partial y}_{K\times N}\in \R^{M\times N}
∂x∂z=∂x∂yM×K∂y∂zK×N∈RM×N
若
X
∈
R
M
×
N
X\in R^{M\times N}
X∈RM×N ，
{
y
i
=
g
i
(
X
)
y
=
[
g
1
(
X
)
,
g
2
(
X
)
,
⋯
,
g
K
(
X
)
]
∈
R
K
z
i
=
f
(
y
)
∈
R
\begin{cases} y_i=g_i(X)&y=[g_1(X),g_2(X),\cdots,g_K(X)]\in \R^{K}\\ z_i=f(y)\in \R \end{cases}
{yi=gi(X)zi=f(y)∈Ry=[g1(X),g2(X),⋯,gK(X)]∈RK
则有
∂
z
∂
x
i
j
=
∂
y
∂
x
i
j
1
×
K
∂
z
∂
y
K
×
1
∈
R
\frac{\partial z}{\partial x_{ij}}=\frac{\partial y}{\partial x_{ij}}_{1\times K}\frac{\partial z}{\partial y}_{K\times 1}\in \R
∂xij∂z=∂xij∂y1×K∂y∂zK×1∈R
更为高效的参数学习
梯度下降法需要计算损失函数对参数的偏导数，如果通过链式法则逐一对每个参数求偏导，会很低效
- 反向传播算法
- 自动梯度计算
反向传播算法
目标
求解
W
(
l
)
←
W
(
l
)
−
α
∂
R
(
W
,
b
)
∂
W
(
l
)
←
W
(
l
)
−
α
(
1
N
∑
i
=
1
N
∂
L
(
y
i
,
y
^
i
)
∂
W
(
l
)
+
λ
W
(
l
)
)
b
(
l
)
←
b
(
l
)
−
α
∂
R
(
W
,
b
)
∂
b
(
l
)
←
b
(
l
)
−
α
(
1
N
∑
i
=
1
N
∂
L
(
y
i
,
y
^
i
)
∂
b
(
l
)
)
\begin{aligned} W^{(l)}&\leftarrow W^{(l)}-\alpha\frac{\partial \mathcal{R}(W,b)}{\partial W^{(l)}}\\ &\leftarrow W^{(l)}-\alpha\left(\frac{1}{N}\sum\limits_{i=1}^N\frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial W^{(l)}}+\lambda W^{(l)}\right)\\ b^{(l)}&\leftarrow b^{(l)}-\alpha\frac{\partial \mathcal{R}(W,b)}{\partial b^{(l)}}\\ &\leftarrow b^{(l)}-\alpha\left(\frac{1}{N}\sum\limits_{i=1}^N\frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial b^{(l)}}\right) \end{aligned}
W(l)b(l)←W(l)−α∂W(l)∂R(W,b)←W(l)−α(N1i=1∑N∂W(l)∂L(yi,y^i)+λW(l))←b(l)−α∂b(l)∂R(W,b)←b(l)−α(N1i=1∑N∂b(l)∂L(yi,y^i))
可见参数求解的核心部分为
∂
L
(
y
i
,
y
^
i
)
∂
W
(
l
)
\frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial W^{(l)}}
∂W(l)∂L(yi,y^i) ，对于矩阵求导，可以对逐个元素求导，再排列为矩阵形式，根据链式法则
∂
L
(
y
i
,
y
^
i
)
∂
w
i
j
(
l
)
=
∂
z
(
l
)
∂
w
i
j
(
l
)
∂
L
(
y
i
,
y
^
i
)
∂
z
(
l
)
∂
L
(
y
i
,
y
^
i
)
∂
b
(
l
)
=
∂
z
(
l
)
∂
b
(
l
)
∂
L
(
y
i
,
y
^
i
)
∂
z
(
l
)
\frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial w_{ij}^{(l)}}=\frac{\partial z^{(l)}}{\partial w^{(l)}_{ij}}\frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial z^{(l)}}\\ \frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial b^{(l)}}=\frac{\partial z^{(l)}}{\partial b^{(l)}}\frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial z^{(l)}}
∂wij(l)∂L(yi,y^i)=∂wij(l)∂z(l)∂z(l)∂L(yi,y^i)∂b(l)∂L(yi,y^i)=∂b(l)∂z(l)∂z(l)∂L(yi,y^i)
计算
∂
z
(
l
)
∂
w
i
j
(
l
)
\frac{\partial z^{(l)}}{\partial w^{(l)}_{ij}}
∂wij(l)∂z(l)
因
z
M
l
×
1
(
l
)
=
W
M
l
×
M
l
−
1
(
l
)
a
M
l
−
1
×
1
(
l
−
1
)
+
b
M
l
(
l
)
z^{(l)}_{M_l\times 1}=W^{(l)}_{M_{l}\times M_{l-1}}a^{(l-1)}_{M_{l-1}\times 1}+b^{(l)}_{M_{l}}
zMl×1(l)=WMl×Ml−1(l)aMl−1×1(l−1)+bMl(l)
- 分母布局，故需要将 z ( l ) z^{(l)} z(l) 转置求偏导，第 i i i 个元素为 a j ( l − 1 ) a_j^{(l-1)} aj(l−1)
计算
∂
z
(
l
)
∂
b
(
l
)
\frac{\partial z^{(l)}}{\partial b^{(l)}}
∂b(l)∂z(l)
计算
∂
L
(
y
i
,
y
^
i
)
∂
z
(
l
)
\frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial z^{(l)}}
∂z(l)∂L(yi,y^i)
计算误差项
∂
L
(
y
i
,
y
^
i
)
∂
z
(
l
)
\frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial z^{(l)}}
∂z(l)∂L(yi,y^i) 表示第
l
l
l 层神经元对最终损失的影响，也反映了最终损失对第
l
l
l 层神经元的敏感程度，不同神经元对网络能力的贡献程度，从而比较好地解决了贡献度分配问题
δ
(
l
)
=
Δ
∂
L
(
y
i
,
y
^
i
)
∂
z
(
l
)
=
[
∂
L
(
y
i
,
y
^
i
)
∂
z
1
(
l
)
∂
L
(
y
i
,
y
^
i
)
∂
z
2
(
l
)
⋮
∂
L
(
y
i
,
y
^
i
)
∂
z
M
l
(
l
)
]
=
Δ
[
δ
1
(
l
)
δ
2
(
l
)
⋮
δ
M
l
(
l
)
]
∈
R
M
l
×
1
\delta^{(l)}\overset{\Delta}{=}\frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial z^{(l)}}=\left[ \begin{matrix} \frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial z_1^{(l)}}\\ \frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial z_2^{(l)}}\\ \vdots\\ \frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial z_{M_l}^{(l)}} \end{matrix} \right]\overset{\Delta}{=}\left[ \begin{matrix} \delta_1^{(l)}\\ \delta_2^{(l)}\\ \vdots\\ \delta_{M_l}^{(l)} \end{matrix} \right]\in \R^{M_l\times 1}
δ(l)=Δ∂z(l)∂L(yi,y^i)=∂z1(l)∂L(yi,y^i)∂z2(l)∂L(yi,y^i)⋮∂zMl(l)∂L(yi,y^i)=Δδ1(l)δ2(l)⋮δMl(l)∈RMl×1
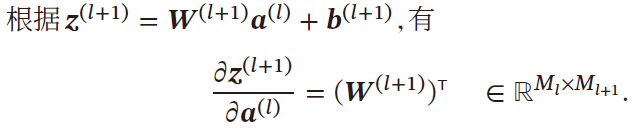
z ( l + 1 ) ∈ R M l + 1 z^{(l+1)}\in \R^{M_{l+1}} z(l+1)∈RMl+1 ， a ( l ) ∈ R M l a^{(l)}\in \R^{M_l} a(l)∈RMl ，所以 z ( l + 1 ) a ( l ) = 分母布局 [ w 11 w 21 ⋯ w M l + 1 1 w 12 w 22 ⋯ w M l + 1 2 ⋮ ⋮ ⋱ ⋮ w 1 M l w 2 M l ⋯ w M l + 1 M l ] ∈ R M l × M l + 1 \frac{z^{(l+1)}}{a^{(l)}}\xlongequal{分母布局}\left[ \begin{matrix} w_{11}&w_{21}&\cdots &w_{M_{l+1}1}\\ w_{12}&w_{22}&\cdots &w_{M_{l+1}2}\\ \vdots&\vdots&\ddots&\vdots\\ w_{1M_l}&w_{2M_l}&\cdots &w_{M_{l+1}M_l}\\ \end{matrix} \right]\in \R^{M_l\times M_{l+1}} a(l)z(l+1)分母布局w11w12⋮w1Mlw21w22⋮w2Ml⋯⋯⋱⋯wMl+11wMl+12⋮wMl+1Ml∈RMl×Ml+1
根据
a
(
l
)
=
f
l
(
z
(
l
)
)
=
(
f
l
(
z
1
(
l
)
)
f
l
(
z
2
(
l
)
)
⋮
f
l
(
z
M
l
(
l
)
)
)
a^{(l)}=f_l(z^{(l)})=\left(\begin{matrix}f_l(z_1^{(l)})\\f_l(z_2^{(l)})\\\vdots\\f_l(z_{M_l}^{(l)})\\\end{matrix}\right)
a(l)=fl(z(l))=fl(z1(l))fl(z2(l))⋮fl(zMl(l)) ，
z
(
l
)
=
(
z
1
(
l
)
z
2
(
l
)
⋮
z
M
l
(
l
)
)
z^{(l)}=\left(\begin{matrix}z_1^{(l)}\\z^{(l)}_2\\\vdots\\z_{M_l}^{(l)}\end{matrix}\right)
z(l)=z1(l)z2(l)⋮zMl(l)，分母布局
∂
a
(
l
)
∂
z
(
l
)
=
∂
f
l
(
z
(
l
)
)
∂
z
(
l
)
=
[
∂
f
l
(
z
1
(
l
)
)
∂
z
1
(
l
)
∂
f
l
(
z
2
(
l
)
)
∂
z
1
(
l
)
⋯
∂
f
l
(
z
M
l
(
l
)
)
∂
z
1
(
l
)
∂
f
l
(
z
1
(
l
)
)
∂
z
2
(
l
)
∂
f
l
(
z
2
(
l
)
)
∂
z
2
(
l
)
⋯
∂
f
l
(
z
M
l
(
l
)
)
∂
z
2
(
l
)
⋮
⋮
⋱
⋮
∂
f
l
(
z
1
(
l
)
)
∂
z
M
l
∂
f
l
(
z
2
(
l
)
)
∂
z
M
l
(
l
)
⋯
∂
f
l
(
z
M
l
(
l
)
)
∂
z
M
l
(
l
)
]
=
[
∂
f
l
(
z
1
(
l
)
)
∂
z
1
(
l
)
0
⋯
0
0
∂
f
l
(
z
2
(
l
)
)
∂
z
2
(
l
)
⋯
0
⋮
⋮
⋱
⋮
0
0
⋯
∂
f
l
(
z
M
l
(
l
)
)
∂
z
M
l
(
l
)
]
=
d
i
a
g
(
∂
f
l
(
z
i
(
l
)
)
∂
z
i
(
l
)
)
∈
R
M
l
×
M
l
,
i
=
1
,
⋯
,
M
l
\begin{aligned} \frac{\partial a^{(l)}}{\partial z^{(l)}}&=\frac{\partial f_l(z^{(l)})}{\partial z^{(l)}}\\ &=\left[ \begin{matrix} \frac{\partial f_l(z_1^{(l)})}{\partial z_1^{(l)}}&\frac{\partial f_l(z_2^{(l)})}{\partial z_1^{(l)}}&\cdots&\frac{\partial f_l(z_{M_l}^{(l)})}{\partial z_{1}^{(l)}}\\ \frac{\partial f_l(z_1^{(l)})}{\partial z_2^{(l)}}&\frac{\partial f_l(z_2^{(l)})}{\partial z_2^{(l)}}&\cdots&\frac{\partial f_l(z_{M_l}^{(l)})}{\partial z_{2}^{(l)}}\\ \vdots&\vdots&\ddots&\vdots\\ \frac{\partial f_l(z_1^{(l)})}{\partial z_{M_l}}&\frac{\partial f_l(z_2^{(l)})}{\partial z_{M_l}^{(l)}}&\cdots&\frac{\partial f_l(z_{M_l}^{(l)})}{\partial z_{M_l}^{(l)}}\\ \end{matrix} \right]=\left[ \begin{matrix} \frac{\partial f_l(z_1^{(l)})}{\partial z_1^{(l)}}&0&\cdots&0\\ 0&\frac{\partial f_l(z_2^{(l)})}{\partial z_2^{(l)}}&\cdots&0\\ \vdots&\vdots&\ddots&\vdots\\ 0&0&\cdots&\frac{\partial f_l(z_{M_l}^{(l)})}{\partial z_{M_l}^{(l)}}\\ \end{matrix} \right]\\ &=diag \left(\frac{\partial f_l(z^{(l)}_i)}{\partial z_i^{(l)}}\right)\in \R^{M_l\times M_l},i=1,\cdots,M_l \end{aligned}
∂z(l)∂a(l)=∂z(l)∂fl(z(l))=∂z1(l)∂fl(z1(l))∂z2(l)∂fl(z1(l))⋮∂zMl∂fl(z1(l))∂z1(l)∂fl(z2(l))∂z2(l)∂fl(z2(l))⋮∂zMl(l)∂fl(z2(l))⋯⋯⋱⋯∂z1(l)∂fl(zMl(l))∂z2(l)∂fl(zMl(l))⋮∂zMl(l)∂fl(zMl(l))=∂z1(l)∂fl(z1(l))0⋮00∂z2(l)∂fl(z2(l))⋮0⋯⋯⋱⋯00⋮∂zMl(l)∂fl(zMl(l))=diag(∂zi(l)∂fl(zi(l)))∈RMl×Ml,i=1,⋯,Ml
[
W
(
l
+
1
)
]
T
⋅
δ
(
l
+
1
)
=
[
w
11
w
21
⋯
w
M
l
+
1
1
w
12
w
22
⋯
w
M
l
+
1
2
⋮
⋮
⋱
⋮
w
1
M
l
w
2
M
l
⋯
w
M
l
+
1
M
l
]
[
δ
1
(
l
+
1
)
δ
2
(
l
+
1
)
⋮
δ
M
l
+
1
(
l
+
1
)
]
=
[
∑
t
=
1
M
l
+
1
w
t
1
δ
t
(
l
+
1
)
∑
t
=
1
M
l
+
1
w
t
2
δ
t
(
l
+
1
)
⋮
∑
t
=
1
M
l
+
1
w
t
M
l
+
1
δ
t
(
l
+
1
)
]
∈
R
M
l
d
i
a
g
(
∂
f
l
(
z
i
(
l
)
)
∂
z
i
(
l
)
)
[
W
(
l
+
1
)
]
T
⋅
δ
(
l
+
1
)
=
[
∂
f
l
(
z
1
(
l
)
)
∂
z
1
(
l
)
0
⋯
0
0
∂
f
l
(
z
2
(
l
)
)
∂
z
2
(
l
)
⋯
0
⋮
⋮
⋱
⋮
0
0
⋯
∂
f
l
(
z
M
l
(
l
)
)
∂
z
M
l
(
l
)
]
[
∑
t
=
1
M
l
+
1
w
t
1
δ
t
(
l
+
1
)
∑
t
=
1
M
l
+
1
w
t
2
δ
t
(
l
+
1
)
⋮
∑
t
=
1
M
l
+
1
w
t
M
l
+
1
δ
t
(
l
+
1
)
]
=
[
∂
f
l
(
z
1
(
l
)
)
∂
z
1
(
l
)
∑
t
=
1
M
l
+
1
w
t
1
δ
t
(
l
+
1
)
⋮
∂
f
l
(
z
i
(
l
)
)
∂
z
i
(
l
)
∑
t
=
1
M
l
+
1
w
t
i
δ
t
(
l
+
1
)
⋮
∂
f
l
(
z
M
l
(
l
)
)
∂
z
M
l
(
l
)
∑
t
=
1
M
l
+
1
w
t
M
l
δ
t
(
l
+
1
)
]
=
Δ
[
δ
1
(
l
)
⋮
δ
i
(
l
)
⋮
δ
M
l
(
l
)
]
\begin{aligned} \left[W^{(l+1)}\right]^T\cdot \delta^{(l+1)}&=\left[ \begin{matrix} w_{11}&w_{21}&\cdots &w_{M_{l+1}1}\\ w_{12}&w_{22}&\cdots &w_{M_{l+1}2}\\ \vdots&\vdots&\ddots&\vdots\\ w_{1M_l}&w_{2M_l}&\cdots &w_{M_{l+1}M_l}\\ \end{matrix} \right]\left[ \begin{matrix} \delta_1^{(l+1)}\\ \delta_2^{(l+1)}\\ \vdots\\ \delta_{M_{l+1}}^{(l+1)} \end{matrix} \right]\\ &=\left[ \begin{matrix} \sum\limits_{t=1}^{M_{l+1}}w_{t1}\delta_t^{(l+1)}\\ \sum\limits_{t=1}^{M_{l+1}}w_{t2}\delta_t^{(l+1)}\\ \vdots\\ \sum\limits_{t=1}^{M_{l+1}}w_{tM_{l+1}}\delta_t^{(l+1)}\\ \end{matrix} \right]\in\R^{M_l}\\ diag \left(\frac{\partial f_l(z^{(l)}_i)}{\partial z_i^{(l)}}\right)\left[W^{(l+1)}\right]^T\cdot \delta^{(l+1)}&=\left[ \begin{matrix} \frac{\partial f_l(z_1^{(l)})}{\partial z_1^{(l)}}&0&\cdots&0\\ 0&\frac{\partial f_l(z_2^{(l)})}{\partial z_2^{(l)}}&\cdots&0\\ \vdots&\vdots&\ddots&\vdots\\ 0&0&\cdots&\frac{\partial f_l(z_{M_l}^{(l)})}{\partial z_{M_l}^{(l)}}\\ \end{matrix} \right]\left[ \begin{matrix} \sum\limits_{t=1}^{M_{l+1}}w_{t1}\delta_t^{(l+1)}\\ \sum\limits_{t=1}^{M_{l+1}}w_{t2}\delta_t^{(l+1)}\\ \vdots\\ \sum\limits_{t=1}^{M_{l+1}}w_{tM_{l+1}}\delta_t^{(l+1)}\\ \end{matrix} \right]\\ &=\left[\begin{matrix} \frac{\partial f_l(z_1^{(l)})}{\partial z_1^{(l)}}\sum\limits_{t=1}^{M_{l+1}}w_{t1}\delta_t^{(l+1)}\\ \vdots\\ \frac{\partial f_l(z_i^{(l)})}{\partial z_i^{(l)}}\sum\limits_{t=1}^{M_{l+1}}w_{ti}\delta_t^{(l+1)}\\ \vdots\\ \frac{\partial f_l(z_{M_l}^{(l)})}{\partial z_{M_l}^{(l)}}\sum\limits_{t=1}^{M_{l+1}}w_{tM_{l}}\delta_t^{(l+1)} \end{matrix} \right]\overset{\Delta}{=}\left[\begin{matrix} \delta^{(l)}_1\\ \vdots\\ \delta^{(l)}_i\\ \vdots\\ \delta^{(l)}_{M_l}\\ \end{matrix} \right] \end{aligned}
[W(l+1)]T⋅δ(l+1)diag(∂zi(l)∂fl(zi(l)))[W(l+1)]T⋅δ(l+1)=w11w12⋮w1Mlw21w22⋮w2Ml⋯⋯⋱⋯wMl+11wMl+12⋮wMl+1Mlδ1(l+1)δ2(l+1)⋮δMl+1(l+1)=t=1∑Ml+1wt1δt(l+1)t=1∑Ml+1wt2δt(l+1)⋮t=1∑Ml+1wtMl+1δt(l+1)∈RMl=∂z1(l)∂fl(z1(l))0⋮00∂z2(l)∂fl(z2(l))⋮0⋯⋯⋱⋯00⋮∂zMl(l)∂fl(zMl(l))t=1∑Ml+1wt1δt(l+1)t=1∑Ml+1wt2δt(l+1)⋮t=1∑Ml+1wtMl+1δt(l+1)=∂z1(l)∂fl(z1(l))t=1∑Ml+1wt1δt(l+1)⋮∂zi(l)∂fl(zi(l))t=1∑Ml+1wtiδt(l+1)⋮∂zMl(l)∂fl(zMl(l))t=1∑Ml+1wtMlδt(l+1)=Δδ1(l)⋮δi(l)⋮δMl(l)
合并求梯度
∂
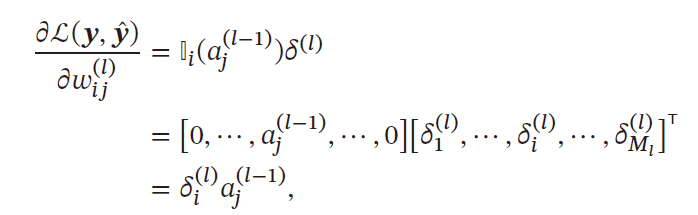
L
(
y
i
,
y
^
i
)
∂
w
i
j
(
l
)
=
[
0
,
⋯
,
a
j
(
l
−
1
)
,
⋯
0
]
[
δ
1
(
l
)
⋮
δ
i
(
l
)
⋮
δ
M
l
(
l
)
]
=
a
j
(
l
−
1
)
δ
i
(
l
)
=
a
j
(
l
−
1
)
∂
f
l
(
z
i
(
l
)
)
∂
z
i
(
l
)
∑
t
=
1
M
l
+
1
w
t
i
δ
t
(
l
+
1
)
⟺
[
δ
(
l
)
⋅
a
(
l
−
1
)
]
i
j
即
[
∂
L
(
y
i
,
y
^
i
)
∂
W
(
l
)
]
i
j
=
[
δ
(
l
)
⋅
a
(
l
−
1
)
]
i
j
\begin{aligned} \frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial w_{ij}^{(l)}}&=\left[0,\cdots,a_j^{(l-1)},\cdots 0\right]\left[\begin{matrix} \delta^{(l)}_1\\ \vdots\\ \delta^{(l)}_i\\ \vdots\\ \delta^{(l)}_{M_l}\\ \end{matrix} \right]\\ &=a_j^{(l-1)}\delta^{(l)}_i=a^{(l-1)}_j\frac{\partial f_l(z_i^{(l)})}{\partial z_i^{(l)}}\sum\limits_{t=1}^{M_{l+1}}w_{ti}\delta_t^{(l+1)}\\ &\iff \left[\delta^{(l)}\cdot a^{(l-1)}\right]_{ij}\\ 即\left[\frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial W^{(l)}}\right]_{ij}&=\left[\delta^{(l)}\cdot a^{(l-1)}\right]_{ij} \end{aligned}
∂wij(l)∂L(yi,y^i)即[∂W(l)∂L(yi,y^i)]ij=[0,⋯,aj(l−1),⋯0]δ1(l)⋮δi(l)⋮δMl(l)=aj(l−1)δi(l)=aj(l−1)∂zi(l)∂fl(zi(l))t=1∑Ml+1wtiδt(l+1)⟺[δ(l)⋅a(l−1)]ij=[δ(l)⋅a(l−1)]ij
故梯度
∂
L
(
y
i
,
y
^
i
)
∂
W
(
l
)
\frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial W^{(l)}}
∂W(l)∂L(yi,y^i) 关于第
l
l
l 层权重
W
(
l
)
W^{(l)}
W(l) 的梯度为
∂
L
(
y
i
,
y
^
i
)
∂
W
(
l
)
=
δ
(
l
)
⋅
a
(
l
−
1
)
∈
R
M
l
×
M
l
−
1
\frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial W^{(l)}}=\delta^{(l)}\cdot a^{(l-1)}\in \R^{M_l\times M_{l-1}}
∂W(l)∂L(yi,y^i)=δ(l)⋅a(l−1)∈RMl×Ml−1
同理，
L
(
y
,
y
^
)
\mathcal{L}(y,\hat{y})
L(y,y^) 关于第
l
l
l 层偏置
b
(
l
)
b^{(l)}
b(l) 的梯度为
∂
L
(
y
i
,
y
^
i
)
∂
b
(
l
)
=
δ
(
l
)
∈
R
M
l
\frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial b^{(l)}}=\delta^{(l)}\in \R^{M_l}
∂b(l)∂L(yi,y^i)=δ(l)∈RMl
其中
δ
(
l
)
=
[
∂
f
l
(
z
1
(
l
)
)
∂
z
1
(
l
)
∑
t
=
1
M
l
+
1
w
t
1
δ
t
(
l
+
1
)
⋮
∂
f
l
(
z
i
(
l
)
)
∂
z
i
(
l
)
∑
t
=
1
M
l
+
1
w
t
i
δ
t
(
l
+
1
)
⋮
∂
f
l
(
z
M
l
(
l
)
)
∂
z
M
l
(
l
)
∑
t
=
1
M
l
+
1
w
t
M
l
δ
t
(
l
+
1
)
]
=
f
l
′
(
z
(
l
)
)
⊙
[
(
W
(
l
+
1
)
)
T
δ
(
l
+
1
)
]
\delta^{(l)}=\left[\begin{matrix} \frac{\partial f_l(z_1^{(l)})}{\partial z_1^{(l)}}\sum\limits_{t=1}^{M_{l+1}}w_{t1}\delta_t^{(l+1)}\\ \vdots\\ \frac{\partial f_l(z_i^{(l)})}{\partial z_i^{(l)}}\sum\limits_{t=1}^{M_{l+1}}w_{ti}\delta_t^{(l+1)}\\ \vdots\\ \frac{\partial f_l(z_{M_l}^{(l)})}{\partial z_{M_l}^{(l)}}\sum\limits_{t=1}^{M_{l+1}}w_{tM_{l}}\delta_t^{(l+1)} \end{matrix} \right]=f'_l(z^{(l)})\odot \left[\left(W^{(l+1)}\right)^T\delta^{(l+1)}\right]
δ(l)=∂z1(l)∂fl(z1(l))t=1∑Ml+1wt1δt(l+1)⋮∂zi(l)∂fl(zi(l))t=1∑Ml+1wtiδt(l+1)⋮∂zMl(l)∂fl(zMl(l))t=1∑Ml+1wtMlδt(l+1)=fl′(z(l))⊙[(W(l+1))Tδ(l+1)]
误差的反向传播
第
l
l
l 层的误差项可以通过第
l
+
1
l+1
l+1 层的误差项计算得到，这就是 **误差的反向传播**
第
l
l
l 层的一个神经元的误差项是与该神经元相连的第
l
+
1
l+1
l+1 层的神经元的误差项的权重和，然后，再乘上该神经元激活函数的梯度。
算法过程
在计算出每一层的误差项后，就可以求得本层的梯度，可以用随机梯度下降法来训练前馈神经网络
- 前馈计算每一层的净输入 z ( l ) z^{(l)} z(l) 和净激活值 a ( l ) a^{(l)} a(l) ，直至最后一层
- 反向传播计算每一层的误差项 δ ( l ) \delta^{(l)} δ(l)
- 计算每一层的偏导数，并更新参数
自动梯度计算
神经网络的参数主要通过梯度下降来优化，需要手动用链式求导来计算风险函数对每个参数的梯度，并转换为计算机程序。
- 手动计算并转换为计算机程序的过程容易出错
目前，主流的深度学习框架都包含了自动梯度计算功能，只需要考虑网络结构并用代码实现，大大提高了开发效率
数值微分
用数值方法计算函数
f
(
x
)
f(x)
f(x) 的导数
f
′
(
x
)
=
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
f'(x)=\lim\limits_{\Delta x\rightarrow 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}
f′(x)=Δx→0limΔxf(x+Δx)−f(x)
- 找到一个合适的 Δ x \Delta x Δx 十分困难- Δ x \Delta x Δx 过小，会引起数值计算问题，舍入误差- Δ x \Delta x Δx 过大，会增加截断误差（受模型影响的理论值与数值解之间的误差）在实际应用中，经常使用以下公式计算梯度，减少截断误差 f ′ ( x ) = lim Δ x → 0 f ( x + Δ x ) − f ( x + Δ x ) 2 Δ x f'(x)=\lim\limits_{\Delta x\rightarrow 0} \frac{f(x+\Delta x)-f(x+\Delta x)}{2\Delta x} f′(x)=Δx→0lim2Δxf(x+Δx)−f(x+Δx)
- 数值微分另一个问题是计算复杂度假设参数数量为 N N N ，则每个参数都需要单独施加扰动，并计算梯度。假设每次正向传播的计算复杂度为 O ( N ) O(N) O(N) ，则计算数值微分的总体时间复杂度为 O ( N 2 ) O(N^2) O(N2)
符号微分
符号计算一般来讲是对输入的表达式，用计算机来通过迭代或递归使用一些事先定义的规则进行转换．当转换结果不能再继续使用变换规则时，便停止计算．
- 一般包括对数学表达式的化简、因式分解、微分、积分、解代数方程、求解常微分方程等运算
符号微分可以在编译时就计算梯度的数学表示，并进一步利用符号计算方法进行优化
且符号计算与平台无关，可在CPU或GPU上运行
缺点：
- 编译时间较长，特别是对于循环，需要很长时间进行编译
- 为了进行符号微分，一般需要设计一种专门的语言来表示数学表达式，并且要对变量（符号）进行预先声明
- 很难对程序进行调试
自动微分
符号微分：处理数学表达式
自动微分：处理一个函数或一段程序
基本原理：所欲偶的数值计算可以分解为一些基本操作，包含+, −, ×, / 和一些初等函数exp, log, sin, cos 等，然后利用链式法则来自动计算一个复合函数的梯度
以
f
(
x
;
w
,
b
)
=
1
e
x
p
(
−
(
w
x
+
b
)
)
+
1
f(x;w,b)=\frac{1}{exp(-(wx+b))+1}
f(x;w,b)=exp(−(wx+b))+11 为例，其中
x
x
x 为输入标量，
w
,
b
w,b
w,b 为权重和偏置
计算图
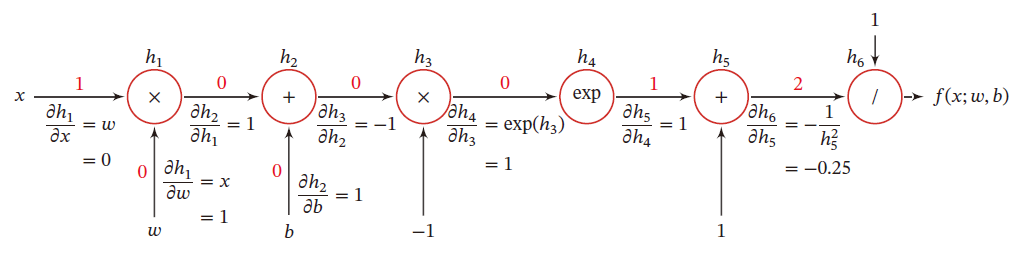
复合函数关于参数的导数可以通过计算图路径上节点的所有导数连乘法得到
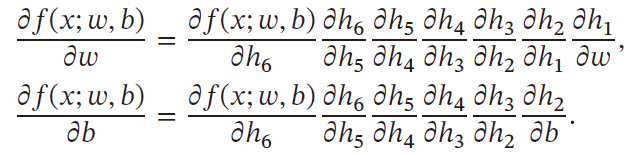
如果函数与参数之间有多条路径，则将这些路径上的导数相加，可以得到最终的梯度
根据计算导数的顺序，自动微分可以分为：前向模式和反向模式
- 前向模式：按照计算图中与参数计算方向相同的方向来递归计算梯度
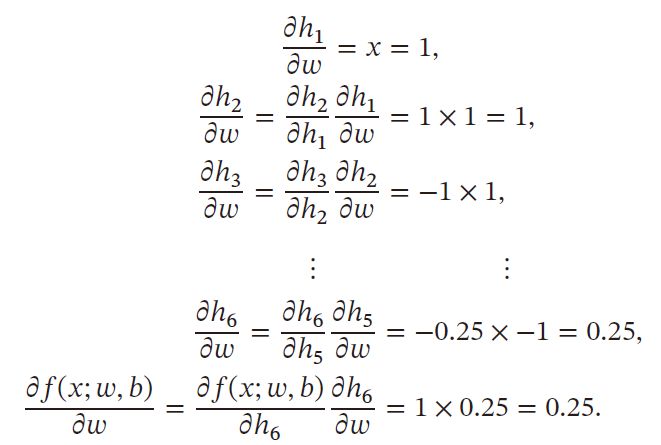
- 反向模式：按照计算图中与参数计算方向相反的方向来计算梯度
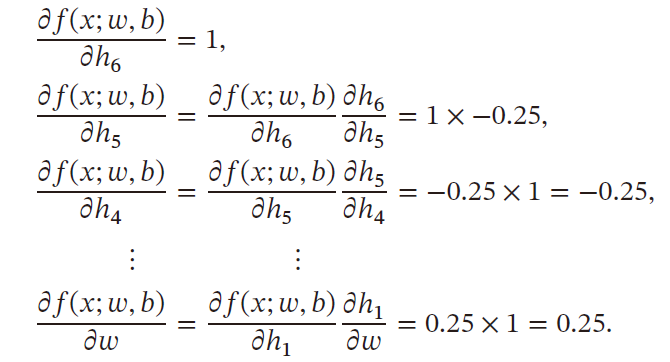反向模式与反向传播的梯度计算方式相同
准则：
当输入变量的数量大于输出变量的数量，用反向模式
- 前向模式需要对每一个输入都进行遍历
- 反向模式需要对每一个输出都进行遍历
在前馈神经网络中，风险函数为
f
:
R
N
→
R
f:\R^{N}\rightarrow \R
f:RN→R 输出为标量，采用反向模式，内存占用小，只需要计算一遍
静态计算图和动态计算图
静态计算图：在编译时构建计算图，运行过程中不可修改
- 在构建时可以进行优化，并行能力强
- 灵活性差
动态计算图：在程序运行时构建计算图
- 不容易优化，输入不同结构的网络，难以并行计算
- 灵活性高
自动微分与符号微分区别
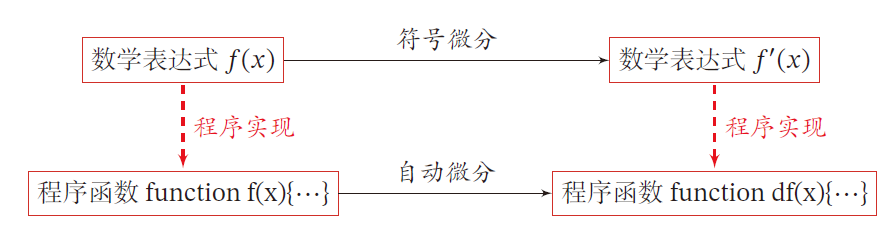
符号微分和自动微分都用计算图和链式法则自动求导
符号微分：
- 符号微分在编译阶段先构造一个符合函数的计算图，通过符号计算得到导数表达式，并对表达式进行优化
- 在程序运行运行阶段才代入变量数值计算导数
自动微分：
- 无需事先编译，程序运行阶段，边计算边记录计算图
- 计算图上的局部梯度都直接代入数值进行计算，然后用前向或反向模式计算最终梯度
优化问题
神经网络的参数学习比线性模型更加困难
- 非凸优化问题
- 梯度消失问题
非凸优化问题
神经网络的优化问题是一个非凸优化问题
y
=
σ
(
w
2
σ
(
w
1
x
)
)
y=\sigma(w_2\sigma(w_1x))
y=σ(w2σ(w1x))
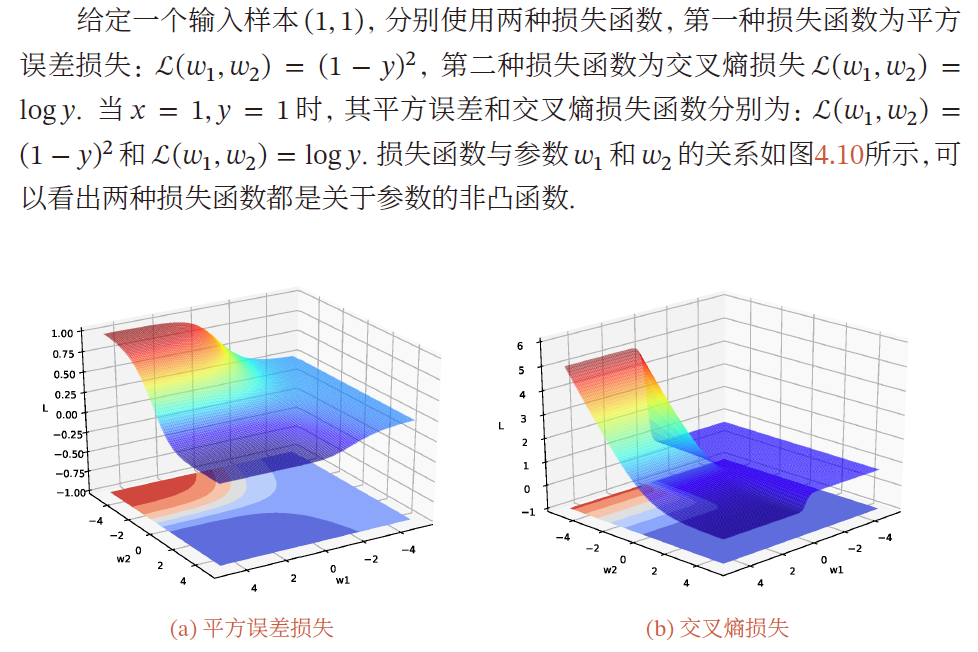
梯度消失问题
在神经网络中，误差反向传播的迭代公式为
δ
(
l
)
=
f
l
′
(
z
(
l
)
)
⊙
[
(
W
(
l
+
1
)
)
T
δ
(
l
+
1
)
]
\delta^{(l)}=f'_l(z^{(l)})\odot \left[\left(W^{(l+1)}\right)^T\delta^{(l+1)}\right]
δ(l)=fl′(z(l))⊙[(W(l+1))Tδ(l+1)]
误差在反向传播时，在每一层都要乘以该层激活函数的导数
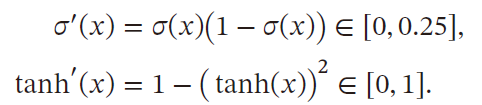
S
S
S 型激活函数的导数值域都
≤
1
\le 1
≤1
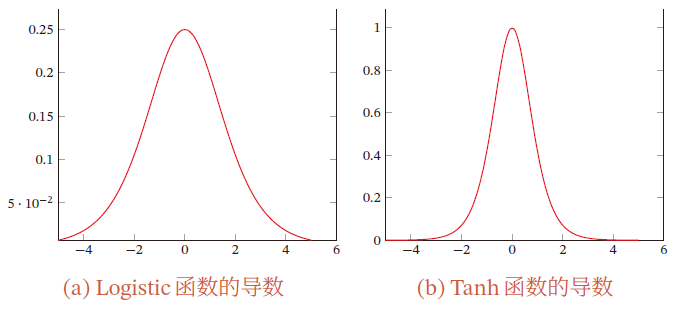
在饱和区导数接近于0，这样误差经过每一层传递会不断衰减，当网络层数很深时，梯度就会不断衰减， 甚至消失，这就是梯度消失问题
- 可以采用导数比较大的激活函数，ReLU函数
1.1.5 全连接的前馈神经网络问题
参数太多
应用于图像处理领域，如果输入图像的像素为
100
×
100
×
3
100\times 100\times 3
100×100×3 ，在全连接网络中，第一层隐藏层的每个神经元到输入层都有
100
×
100
×
3
=
30000
100\times 100\times3=30000
100×100×3=30000 个互相独立的连接，相应的有
30000
30000
30000 个权重参数，随着隐藏层的神经元数量增多，参数的规模也会急剧增加
局部不变性
自然图像中的问题有局部不变形，比如尺寸缩放、平移、旋转等操作不影响语义特征，但全连接的前馈神经网络很难提取这些局部不变的特征——数据增强
本文转载自: https://blog.csdn.net/qq_40479037/article/details/133707385
版权归原作者 AmosTian 所有， 如有侵权，请联系我们删除。
版权归原作者 AmosTian 所有， 如有侵权，请联系我们删除。