首先就要说到中文分词 现阶段的分词手法一般有三大流派
1.基于规则: 前后向最大匹配
2.基于统计:HMM, CRF
3.基于深度学习:Bilstm+crf
那么我们今天重点要讲的就是其中之一HMM隐马尔可夫模型
再说一下为什么要进行分词?
1.更好的理解语义(能够提高模型性能)
2.为了更重要的任务 如(命名实体识别、情感分析、文本分类 、语义识别等等)
3.应用场景的需要 (淘宝、百度)搜索算法对于分词的要求就非常高
But 并非所有中文任务都需要进行分词! 比如说 Bert (NSP)
然后绕不开的一个点就是**语料库 **
想要有好的分词效果 那就必须要有高质量的语料库 (高质量语料库一般都由人工标注完成)
 这里我截取了一个小的语料库
这里我截取了一个小的语料库
我们将每一行 都看成是一篇文章 每篇文章用空格隔开 这里的语料库是基于分词的语料库 是用来帮助我们分词的 也有词性标注语料库 情感分析语料库等等
然后就要说到我们分词的一个标识问题了
每个字都有一个标识(我们也可以叫做隐藏状态)我们可以根据我们的隐藏状态得到所有的标识
B:词语开始
M:词语中间
E:词语结束
S:单独成词
那么我们中文分词的最终目的是什么呢?
就是为了得到状态!
举个例子: 我正在写博客! 那么相对应的BMES标识是 SBEBMES
**那么我们就可以根据一直状态进行分词 即在‘E’ 'S'后面输出空格即可 那么我们输出的分词结果就是 我[空格]正在[空格]写博客[空格]![空格] **
这就是我们平时一直说的中文分词的底层逻辑!
我们正常分词的流程怎么走?
首先根据我们的语料库已经分好的词 得到每一个字的状态 就是刚才的BMES
然后再根据每一个字的状态 去统计我们的三个矩阵(初始,转移,发射矩阵)
统计完三个矩阵之后 我们可以很容易的得到有BMES组成的序列 然后就在ES后输出空格 我们分词就结束了
那么我们HMM真正的训练和预测过程是怎样的?
首先说训练过程(实际就是求解上面三个矩阵的过程)这三个矩阵同深度学习的思想可以理解为参数 也就是W和B
那么根据我们求解出来的这三个矩阵 我们在遇到一个新的句子的时候 我们就可以根据这三个矩阵去计算每一个字他的BMES的概率是多少 (也可以说是每一种路径的概率) 然后我们在根据维特比算法去求解出最优路径 也就是我们概率最大的BMES序列分布
看图

还有一个问题就是 这里的维特比算法和HMM其实不是强相关 只是如果HMM不依赖维特比算法 那么它的计算会变得复杂很多
那么我们重点来了** 如何计算初始矩阵 转移矩阵 和发射矩阵?**
首先我们说**初始矩阵 **初始矩阵的作用是:统计每篇文章的第一个字是什么状态
注意 我们一开始统计的都是频次 也就是BMES的频次 后面才转化为概率
那么我们根据统计每篇文章的第一个字是什么状态可以得到一个表格 再由我们的频次转化为概率就是我们初始矩阵做的事情
为了讲的更详细 我们举一个实例
我们用 【今天 天气 真 不错 。】 【麻辣肥牛 好吃 !】 【我 喜欢 吃 好吃 的!】 这三个句子来做我们的语料库
对应的BMES的序列为【BEBESBES】 【BMMEBES】 【SBESBESS】 这三个句子来做我们的语料库 那么我们得到的初始矩阵就是如下图所示

然后就是我们的转移矩阵:(就是当前状态到下一状态的概率)
这里可以通俗解释一下 就是 当前这个字的状态是B 那么下一个字的状态是什么? BMES中的哪一个?那么我们就可以列成一个矩阵
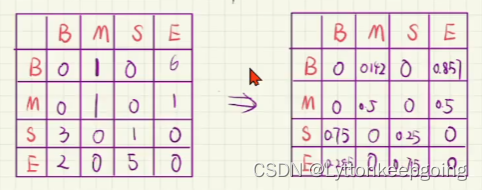
由这个矩阵我们可以看到 B后面接B的有0个 B后面接M的有1个 B后面接S的有0个 B后面接E的有6个 依次类推 那么我们可以根据每个转移状态的的个数 得出概率 (注意 我们这是横着看的)
接下来就是发射矩阵:(统计某种状态下,所有字出现的次数(概率))
就是BMES 有哪些字是B 哪些字是E MS 依次遍历语料库中的每一个字
得到的矩阵为下 实际上是一个双重字典

那么得到这三个矩阵之后 我们的训练部分就完成了
接下来就是预测过程:(给到一个新句子 根据我们的三个矩阵 得到BMES的序列)
那么为了方便 我们同样举一个简单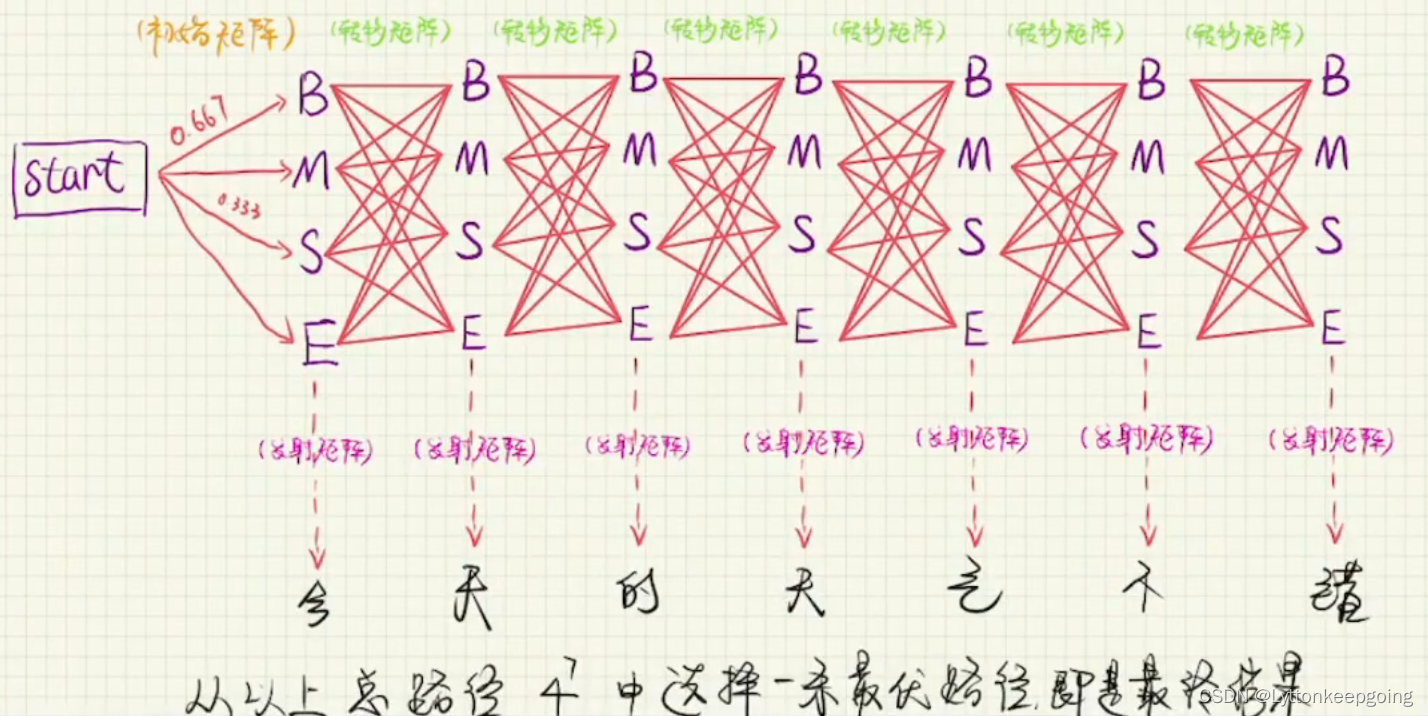 的例子【今天的天气真不错】==》【BESBEBE】
的例子【今天的天气真不错】==》【BESBEBE】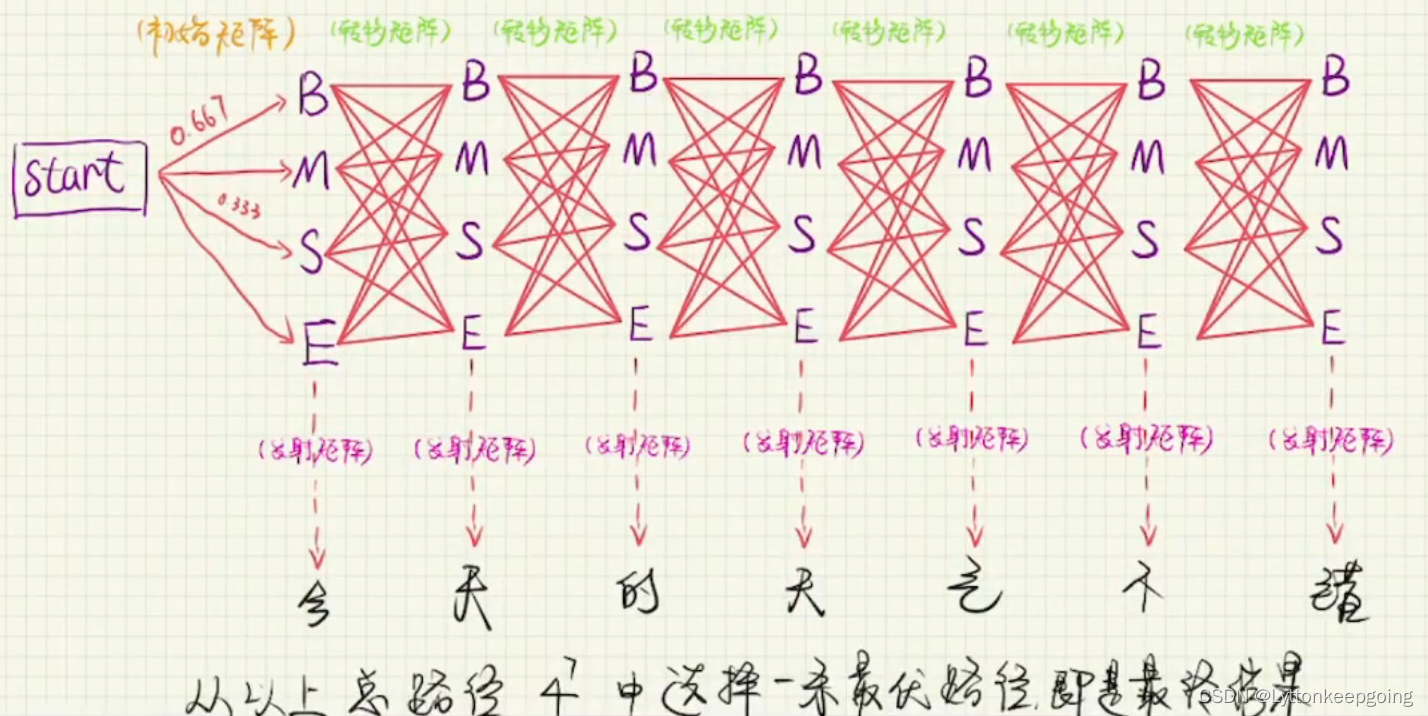
这句话是七个字 每一个字有四种状态 那么他的路线总数一共就有4^7 每一条路线我们都要计算概率
首先 上来查找初始矩阵 然后得到第一个 BS的概率分别为0.667和0.333 那么如果我们往B转移的同时 他的发射矩阵同样也有一个概率 就是B为今的概率 从上图可以知道为0.142 那么从今往下一个字转移 那么我们就要查询 转移矩阵 得知 B往E转移的概率为0.857 同时我们也要查询一下发射矩阵 E为天的概率 那么依次类推下去我们就可以查询出所有路径的概率 就是4^7个概率
那么我们要如何快速的得到我们的最有路径 那么就要用到我们的维特比算法
维特比算法的核心思想就是边计算边删除那些概率比较小的路径
从开始初始矩阵赋值开始计算 如上图 要想到达第二个B 也就是如果天是B 那么将会有四条路经到达第二个B 那么这四个路径中必然有一条最优路径 且 找出最优路径的同时删除其他非最优路径 同理到达第二个MSE 都会存在一条最优路径 维特比算法的核心思想还有一点就是 如果当前路径是最优路径 那么到达上一个节点的路径也必然是最优路径 那么我们得到这四条最优路径之后 就不能再得出哪一条路径是最优的 因为他们都只是局部最优 那么到达最后一个字的时候仍然保有四条路径 那么这四条路径 我们就可以角逐出谁是真正的全局最优
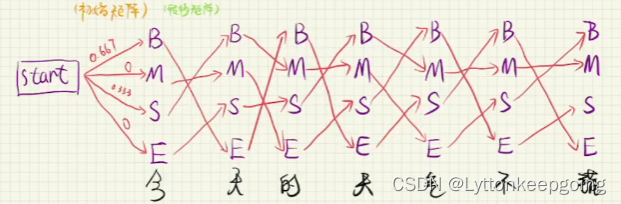
**总结一下就是 根据上面的方法 每到达一个字都只会有4条路经 在4条路径中 选择最优的 则可得到状态序列 分词结束 **
最后呢 就是HMM的代码实现 (注释写得非常清楚 这里就不再详细讲解了)

训练集分布 首先处理训练集 也就是打上BMES由上面的原始语料库生成状态文件 就是下面的all_train_state.txt
下面的这两个函数就是用来生成这个状态文件的
import pickle
from tqdm import tqdm
import numpy as np
import os
def make_label(text_str): # 从单词到label的转化 如:今天 --》BE 麻辣肥牛 --》BMME
text_len = len(text_str)
if text_len == 1:
return 'S'
return 'B' + 'M' * (text_len - 2) + 'E' # 除了开头结尾是BE 其余都是M
def text_to_state(file='all_train_text.txt'): # 将原始的语料库转化为对应的状态文件
if os.path.exists('all_train_state.txt'): # 如果存在该文件 就直接退出
return
all_data = open(file, 'r', encoding='utf-8').read().split('\n')
# 打开文件并按行切分到all_data中 all_data 是一个list
with open('all_train_state.txt', 'w', encoding='utf-8') as f: # 打开写入的文件
for d_index, data in tqdm(enumerate(all_data)): # 逐行遍历
if data: # 如果data不为空
state_ = ""
for w in data.split(" "): # 当前文章按照空格切分 w是文章中的一个词语
if w : # 如果w不为空
state_ = state_ + make_label(w) + " " # 制作单个单词的label
if d_index != len(all_data) - 1: # 最后一行不加'\n' 其余都加
state_ = state_.strip() + '\n' #
f.write(state_)
然后我们定义HMM类 最关键的就是三大矩阵 然后用维特比算法来预测
class HMM:
def __init__(self, file_text = 'all_train_text.txt', file_state = 'all_train_state.txt'):
self.all_states = open(file_state, 'r', encoding='utf-8').read().split('\n') # 按行获取所有的状态
self.all_texts = open(file_text, 'r', encoding='utf-8').read().split('\n') # 按行获取所有的文本
self.states_to_index = {'B': 0, 'M': 1, 'S':2, 'E':3} # 给每一个状态一个索引,以后可以根据状态获取索引
self.index_to_states = ["B", "M", "S", "E"] # 根据索引获取对应状态
self.len_states = len(self.states_to_index) # 状态长度:这里是4 也有bioes
self.init_matrix = np.zero((self.len_states)) # 初始矩阵 1 * 4 对应BMES
self.transfer_matrix = np.zero((self.len_states, self.len_states)) # 转移状态矩阵 4*4
self.emit_matrix = {"B":{"total": 0}, "M":{"total":0}, "S":{"total":0}, "E":{"total":0}}
# 发射矩阵 使用的2级字典 这里初始化了一个total键 储存当前状态出现的总次数 为后面的归一化做准备
def cal_init_matrix(self, state): #计算初始矩阵
self.init_matrix[self.states_to_index[states[0]]] += 1 # BMSE 四种状态 对应状态出现一次加一
def cal_transfer_matrix(self, states): # 计算转移矩阵
sta_join = "".join[states] # 状态转移从当前状态到后一状态 即从sta1到sta2
sta1 = sta_join[:-1]
sta2 = sta_join[1:]
for s1, s2 in zip(sta1, sta2): # 同时遍历s1, s2
self.trainsfer_matrix[self.states_to_index[s1], self.states_to_index[s2]] += 1
def cal_emit_matrix(self, words, states): # 计算发射矩阵
for word , state in zip("".join(words), "".join(states)): # 先把words和states 拼接起来再遍历 因为中间有空格
self.emit_matrix[state][word] = self.emit_matrix[state].get(word, 0) + 1
self.emit_matrix[state]["total"] += 1 # 注意这里多添加了一个total键 储存当前状态出现的总次数 为了后面的归一化使用
def normalize(self):
self.init_matrix = self.init_matrix/np.sum(self.init_matrix)
self.transfer_matrix = self.transfer_matrix/np.sum(self.trainsfer_matrix, axis = 1 , keepdims = True)
self.emit_matrix = {state:{word:t/word_times["total"]*100 for word, t in word_times.items() if word != "total"} for state, word_times in self.emit_matrix.items()}
def train(self):
if os.path.exists("three_matrix.pkl"): # 如果已经存在参数了 就不训练了
self.init_matrix, self.transfer_matrix, self.emit_matrix = pickle.load(open("three_matrix.pkl", "rb"))
return
for words, states in tqdm(zip(self.all_texts, self.all_states)): # 按行读取文件 调用三个矩阵的求解函数
words = words.split(" ") # 在文件中 都按照空格切分
states = states.split(" ")
self.cal_init_matrix(states[0])
self.cal_transfer_matrix(states)
self.cal_emit_matrix(words, states)
self.normalize() # 矩阵求完之后进行归一化
pickle.dump([self.init_matrix, self.transfer_matrix, self.emit_matrix], open("three_matrix.pkl", "wb")) # 保存参数
def viterbi_t(text, hmm):
states = hmm.index_to_states
emit_p = hmm.emit_matrix
trans_p = hmm.transfer_matrix
states_p = hmm.init_matrix
V = [{}]
path = {}
for y in states:
V[0][y] = start_p[hmm.states_to_index[y]] * emit_p[y].get(text[0], 0)
path[y] = [y]
for t in range(1, len(text)):
V.append({})
newpath = {}
neverSeen = text[t] not in emit_p['S'].keys() and \
text[t] not in emit_p['M'].keys() and \
text[t] not in emit_p['E'].keys() and \
text[t] not in emit_p['B'].keys()
for y in states:
emitP = emit_p[y].get(text[t], 0) if not neverSeen else 1.0 # 设置成未知字单独成词
(prob, state) = max([(V[t-1][y0] * trans_p[hmm.states_to_index[y0], hmm.states_to_index[y]] * emitP, y0) for y0 in states if V[t-1]])
V[t][y] = prob
newpath[y] = path[states] + [y]
path = newapth
(prob. state) = max([(V[len(text)-1][y], y ) for y in state])
result = ""
for t, s in zip(text, path[state]):
result += t
if s == "S" or s == "E" :
result += " "
return result
if __name__ == "__main__":
text_to_state()
text = "输入要分词的句子 "
hmm = HMM()
hmm.train()
result = viterbi_t(text, hmm)
print(result)
版权归原作者 Lyttonkeepgoing 所有, 如有侵权,请联系我们删除。