1. 支持向量机
支持向量机(Support Vector Machine, SVM)是一类按监督学习(supervised learning)方式对数据进行二元分类的广义线性分类器(generalized linear classifier),其决策边界是对学习样本求解的最大边距超平面(maximum-margin hyperplane)。SVM使用铰链损失函数(hinge loss)计算经验风险(empirical risk)并在求解系统中加入了正则化项以优化结构风险(structural risk),是一个具有稀疏性和稳健性的分类器。SVM可以通过核方法(kernel method)进行非线性分类,是常见的核学习(kernel learning)方法之一。SVM被提出于1964年,在二十世纪90年代后得到快速发展并衍生出一系列改进和扩展算法,在人像识别、文本分类等模式识别(pattern recognition)问题中有得到应用。
2. SVM欧式距离
SVM中使用的是欧式距离,高等数学中的立体几何告诉我们,三维空间中所有处于同一平面的点所对应的方程,任何一个平面都可以用三元一次方程来表示。如果知道一个平面的法向量W=(a,b,c),平面内一点P=(x1,y1,z1),平面内任意一点(x,y,z),可以求得与法向量垂直,且过P点的平面。方程如下:
(x-x1)a+(y-y1)b+(z-z1)c=0 (点法式方程)
即满足此方程的所有(x,y,z)点组成了该平面,式子中(x-x1),(y-y1),(z-z1)为这两点组成的向量,展开后方程为ax+by+cz-(ax1+by1+cz1)=0,其中-(ax1+by1+cz1)为常数,为0时表明该平面过原点。
记D=-(ax1+by1+cz1)。由点到面的距离公式得到:
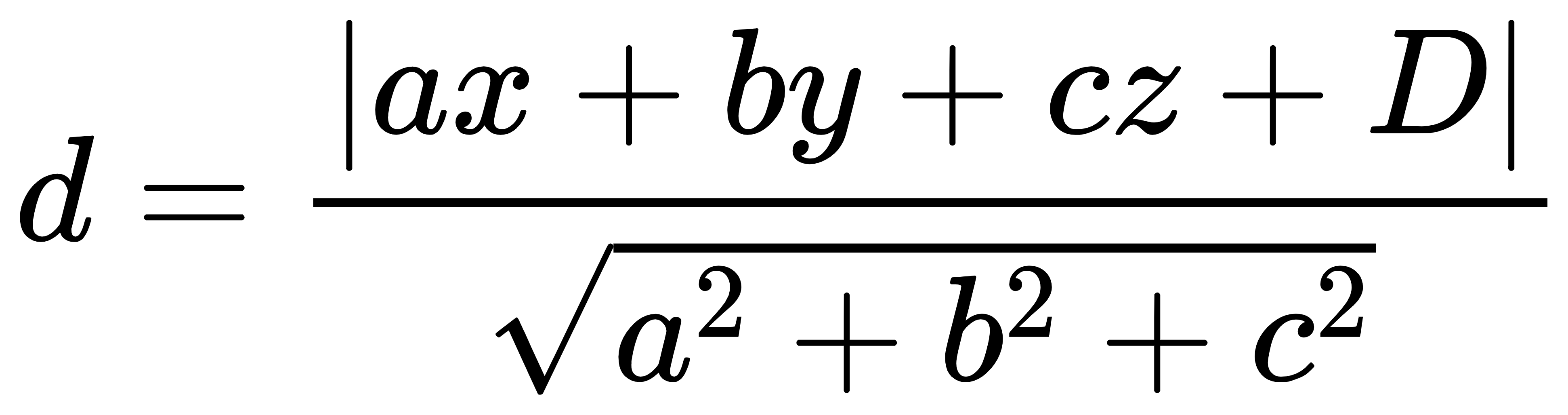
两平面之间的距离公式是:互相平行的两个平面,设两个平面是:ax+by+cz+d=0,ax+by+cz+e=0。那么两平面的距离为:
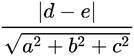
现假设划分超平面的线性方程为:

上式中,W=(w1,w2,…,wn)为法向量坐标,X=(x1,x2,…,xn)为超平面内的满足此方程的任意点坐标。b为位移项,源点到超平面距离与其有关。一旦W与b确定了,由X组成的平面也就确定了。
在三维空间中,已知A1点的坐标与A2点的坐标,且都在平面内;W为该平面的法向量,d为点X到平面的距离。

可以得到
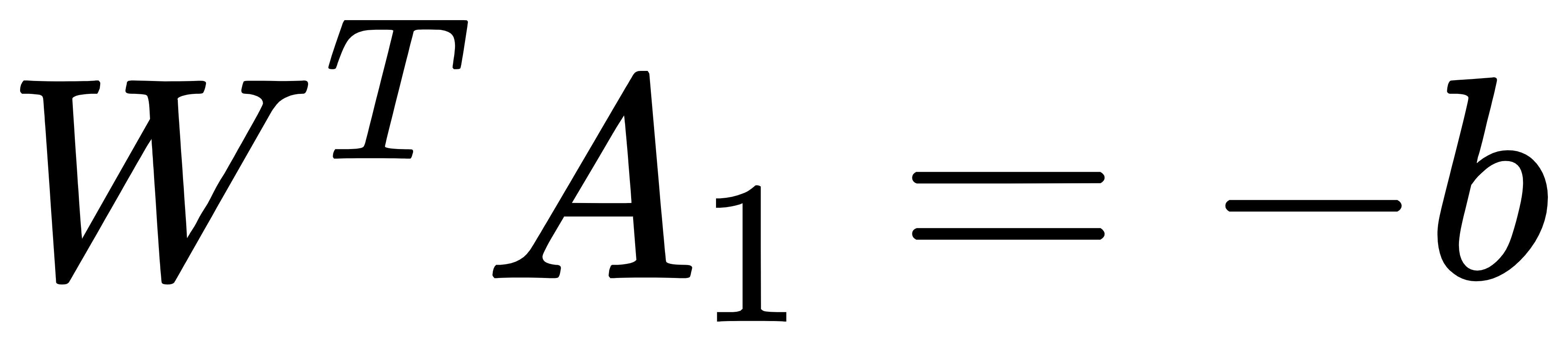

根据图可以由两点的坐标可以计算XA1向量。我们知道向量的内积公式: ab=|a||b|cosθ
所以平面外任意点X到平面的距离公式可以计算如下:
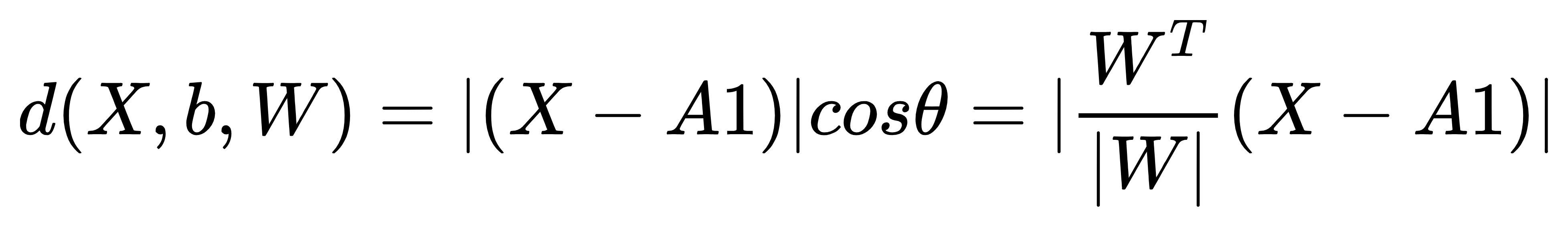
其中WT**/W**为单位法向量。上式进一步化简可得到:

上式中**|W|为二阶范式,三维空间中表示向量的模。二阶范式的计算公式如下:**
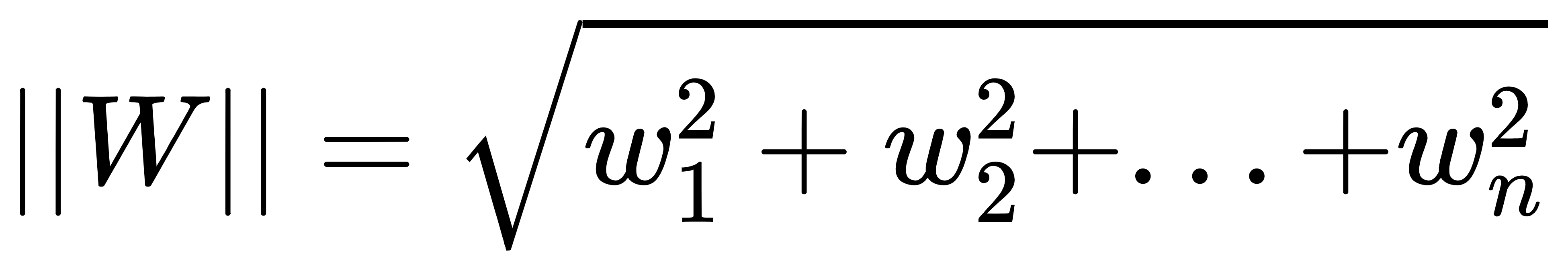
3. 线性可分
前面已经了解到了,SVM是一个线性分类器,通过核函数也可以进行非线性分类。在二维空间或三维空间中,两个点集(D0和D1)被一条直线或者平面完全分开叫做线性可分。

严格的数学定义如下:
D0和D1是n维欧式空间中的两个点集。如果存在n维向量W和实数b,使得所有属于D0的点Xi都有WXi+b>0,所有属于D1的点Xj都有WXi+b<0,则我们称D0与D1线性可分。我们知道在平面直角坐标系与空间直角坐标系中,当点在线上或者平面中时,WX+b=0,当不在线上或者平面时,则WX+b≠0;(在线或者面上方大于0,下方则小于0)。
4. 最大间隔超平面
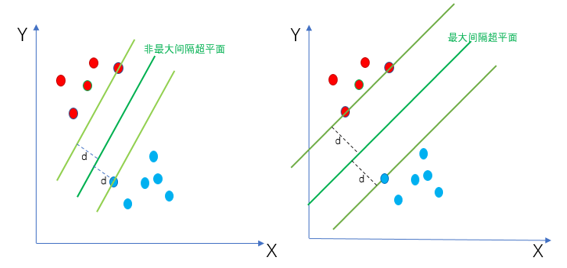
SVM的目标是找到一个最佳的超平面(WX+b=0),将D0与D1进行分开。所谓最佳就是使得离超平面最近的点越远越好,也就是找到最大间隔超平面。如下图所示,左边为任意一个非最大间隔超平面,右边为最大间隔超平面。从图中可以看出最大间隔超平面使得距离超平面最近的点的距离d最大化。距离d越大,表示分类效果越好,鲁棒性越好。
- 支持向量
样本中距离超平面最近的点叫做支持向量。因为这些点对分类的超平面起着决定性的作用,决定了超平面的位置。

6. SVM****目标函数与最优化问题
从上图中我们可以知道支持向量到超平面的距离为d,其他点到超平面的距离均大于d。这里我们定义数据集标签(目标值)的取值为y=1或y=-1,分别表示两个类别。于是,根据前面的距离公式,进一步可以得到如下两个式子:
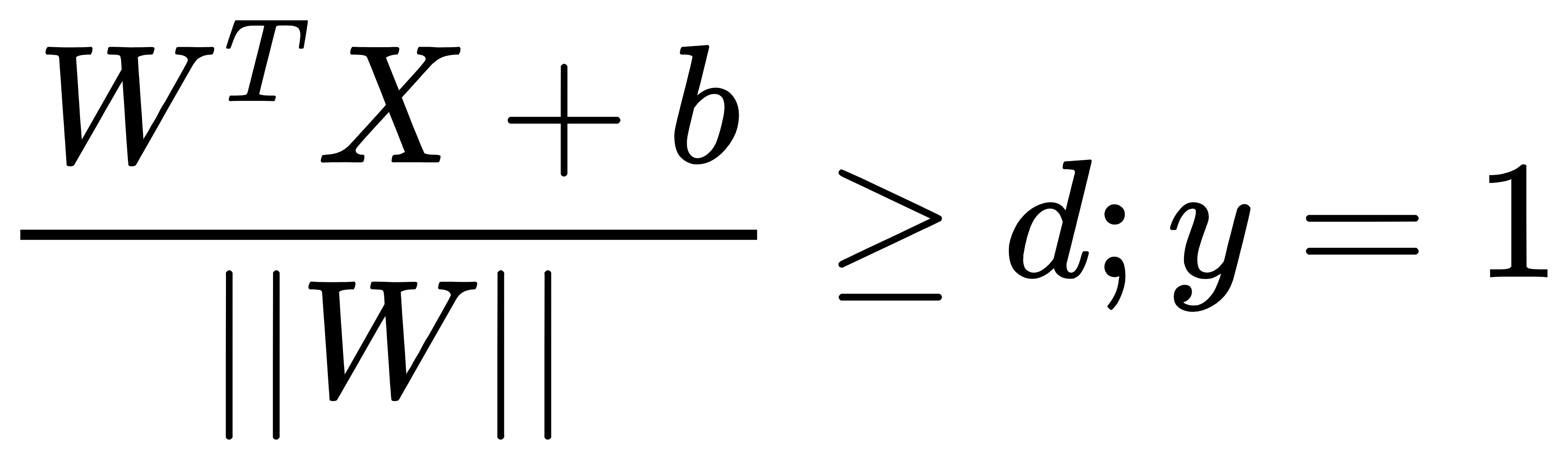

上式中,分子与前面稍有不同,去掉了绝对值,超平面的两侧分别为正值与负值。对上式子进行转换可以得到:

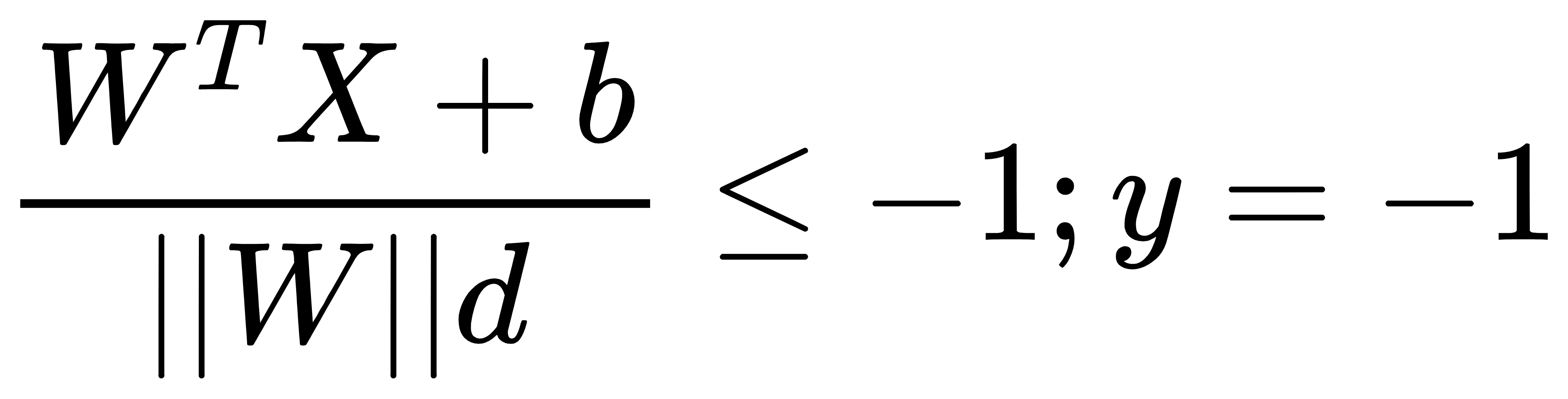
然后我们可以得到最大间隔超平面的上下两个超平面的方程如下图所示。

现在对式子作变量替换,替换如下:

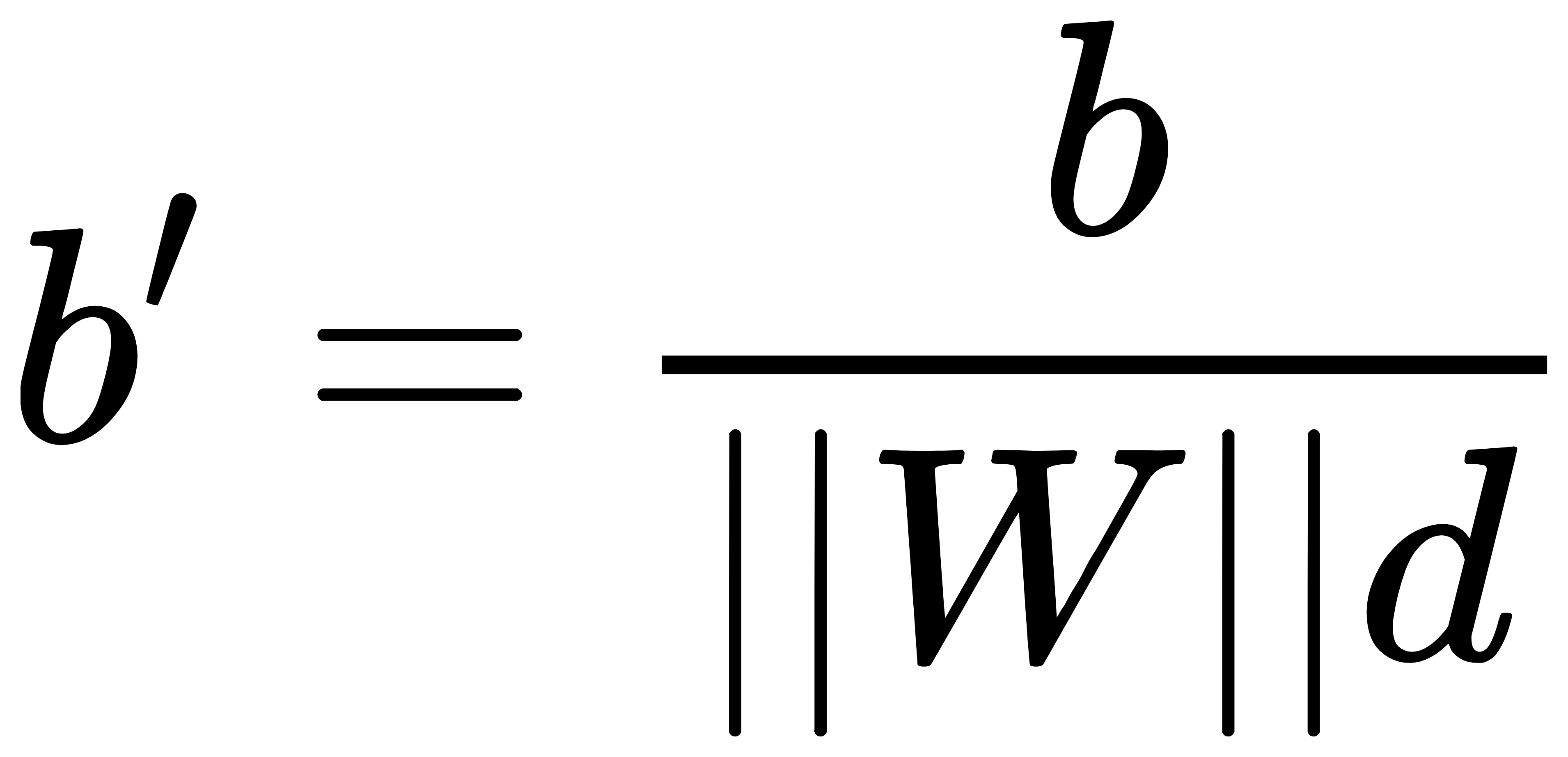
所以上下两个边界(最大间隔超平面边界)的平面方程可以写为下面这样:


同样道理,我们对最大间隔超平面也进行变量伸缩变换,对WTX+b=0等式左右两边同时除以**||W||d**,所表示的超平面没有变化。在使用上面的式子W’与b’替换得到最大间隔超平面的方程为:

由于y的两个类别是-1与1.对于距离公式去掉绝对值后,第i个样本点到最大间隔超平面的距离公式如下:

最大间隔超平面的目标函数(2d的值)可以表示为:

上式中,花括号内是求支持向量(离最大间隔超平面最近的点)到最大间隔超平面的距离。整个式子表示找到使得支持向量到最大间隔超平面的距离最大的情况下,W’,b’的取值。我们知道了最大间隔超平面的上下两个平面的方程,所以支持向量到最大间隔超平面的距离为d,也就是最小值,根据两个平行超平面的公式现在可以求得d的值如下:

所以最大间隔就是2d。在图中表示更清晰,如下:

目标函数(2d的值)则可以进一步表示为:

为了让求解变得简单,上述问题的最大值转换为以下目标函数的最小值:

其约束条件为:

转换后的目标函数的平方是为了去除二阶范式W’的根号,将来计算方便,不改变最优的W’,b’的结果值。
- 拉格朗日乘子法与目标函数求解
拉格朗日乘子法是给定约束条件求极值,现在设z=f(x,y)在条件g(x,y)=0的情况下,在点(x0,y0)处(切点处,只有切点处才是附近的最大或者最小值,否则偏导数如果不等于0,则沿着x或者y方向走一小段距离,则值变大或者变小)取得极值。那么f(x,y)与g(x,y)在该点(x0,y0)处的梯度(两个偏导数所在方向的向量的和)必定平行;

所以(fx′(x0,y0),fy′(x0,y0))(fx′(x0,y0),fy′(x0,y0))与向量(gx′(x0,y0),gy′(x0,y0))(gx′(x0,y0),gy′(x0,y0))平行。所以有
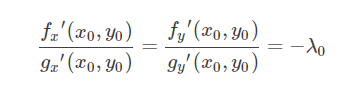
进一步得到:

然后引入辅助函数(拉格朗日函数)L(x,y,λ)=f(x,y)+λg(x,y) ,将条件极值转换为无条件极值问题求解,对该函数求偏导得
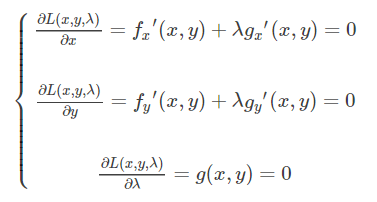
上式为等式约束下的拉格朗日函数,其中所求的偏导数的点为驻点,驻点可能是极值,若实际问题有解,则必为极值。关于拉格朗日乘子法这里不作过多探讨。
下面介绍不等式约束下的拉格朗日乘子法:
对于不等式约束条件的求解,需要满足KKT(Karush-Kuhn-Tucker)条件才能进行求解。以下为KKT问题与条件。
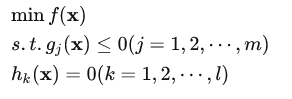
KKT条件给出了判断是否为最优解的必要条件,即:

与前面的等式条件极值相比较,多了个μ大于等于0(具体为什么大于等于0,可以参考https://zhuanlan.zhihu.com/p/26514613)。上式中告诉我们如果gj(X)小于0,则μj=0,,在SVM中表示这些点不是支持向量;若gj(X)=0,则表明约束在边界上,则由梯度关系μj>0,对应支持向量。再回头看W’与b’的式子我们可知道支持向量(其对应的λ大于0)确定了W’与b’的值,其他点对该参数没影响。
构造拉格朗日函数如下:
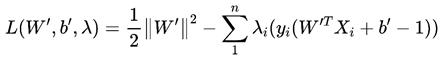
约束条件为:

**8. **拉格朗日对偶问题
对于有约束的最优化问题,可以通过KTT条件把有约束的最优化问题转换成无约束的最优化问题,但是有时候直接求解KKT条件也很困难,可以通过求解原问题的对偶问题来得到原问题的一个下界估计。(对于非凸优化问题,可以用拉格朗日对偶问题来求解)
假设目标函数及约束条件如下:

构造拉格朗日如下:
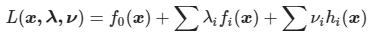
其又可转化为以下形式:
minxmaxλ,νL(x,λ,ν) s.t.λ≥0
即先将x当作常数,把λ,ν当作变量,去求拉格朗日函数的最大值。然后在把x当作变量从中找最小值(上述等价于求min f,此处不作证明)。
对偶问题的一个特性就是,无论原问题是什么,只要换成对偶问题,它都是一个凸优化问题(此处不作证明)。下面给出原问题与对偶问题的解的关系原问题:
minxmaxλ,νL(x,λ,ν) s.t. λ≥0
对偶问题:maxλ,νminxL(x,λ,ν) s.t. λ≥0
那么原问题的解是大于等于对偶问题的解的(引用别人的,此处不作证明)。
** 弱对偶性**
d∗=maxλ,ηθD(λ,η)≤minxθP(x)=p∗
这个性质便是弱对偶性( weak duality )。弱对偶性对任何优化问题都成立,这似乎是显然的,因为这个下界并不严格,有时候甚至取到非常小,对近似原问题的解没多大帮助。
强对偶性
强对偶是是一个非常好的性质,因为在强对偶成⽴的情况下,可以通过求解对偶问题来得到原始问题的解,在 SVM 中就是这样做的。当然并不是所有的对偶问题都满⾜强对偶性,在 SVM 中是直接假定了强对偶性的成⽴,其实只要满一些条件,强对偶性是成⽴的,比如说 Slater 条件(此处不作介绍)与KKT条件。
关于Slater
当Slater条件成立时,KKT条件是最优性的充要条件,此时对偶间隙为零(强对偶性成立)
如果Slater条件不成立,满足KKT条件的解也是最优解。
如果Slater条件不成立,即使优化问题存在全局最优解,也可能不存在解满足KKT条件。
由于原问题是一个图凸二次规划问题,所以原问题利用强对偶性转化:

对W’求偏导:

对b’求偏导:

将上面两个式子代入原目标函数

得到上式如下:
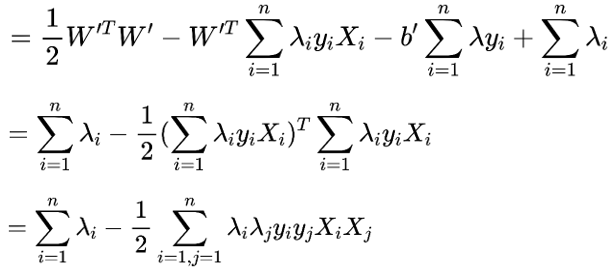
此时,我们求得了min(w,b)最小值,然后再求max(λ)的最大值。所以继续对λ求极大值:

条件为

将上式负号提出来,进一步将极大值转换为求极小值:

如果我们求得了λ,那么W’与b’就都可以求得了。上式是一个二次规划问题,还是比较复杂的,一般采用序列最小优化算法(SMO)求解。
9. SMO****算法
序列最小优化算法(Sequential minimal optimization, SMO)是一种用于解决支持向量机训练过程中所产生优化问题的算法。SMO由微软研究院的约翰·普莱特于1998年发明被广泛使用于SVM的训练过程中。1998年,SMO算法发表在SVM研究领域内引起了轰动,因为先前可用的SVM训练方法必须使用复杂的方法,并需要昂贵的第三方二次规划工具。而SMO算法较好地避免了这一问题。
由于目标函数为凸函数,一般的优化算法都通过梯度方法一次优化一个变量求解二次规划问题的最大值,但是,对于以上问题,由于限制条件

的存在,没办法一次只更新一个参数。为了克服以上的困难,SMO采用一次更新两个变量的方法。具体步骤如下:
现在假设需要更新的参数为λi, λj,固定其他参数可以得到下面约束:
λiyi+λjyj=C , λi≥0, λj≥0
其中

所以

这样就把目标问题转换为了只有一个约束条件的最优化问题。
对于只有一个约束条件的最优化问题,完全可以在λi上对优化目标求偏导,令导数为0,从而求出变量λinew,然后根据λinew求出λjnew。
多次迭代直至收敛。通过SMO求得最优解λ※。(迭代求解过程仍然很复杂,下面具体讲解SMO算法优化目标函数)
我们知道SMO算法是一次性优化两个变量。假设要优化的两个变量(关于如何选取这两个变量,后面有讲)为λ1,λ2,那么约束条件如下:
λ1y1+λ2y2=C
假设λi取值范围为[0,t]。由于y1,y2取值为1或-1。λ1,λ2在[0,t]和[0,t]矩形区域内,并且两者的关系直线只能为1或者-1。当y1与y2不同号时,无非两种情况,第一种是λ1-λ2=k,也就是λ2=λ1-k。第二种情况是λ2=λ1-k。 所以当y1与y2异号时,λ1,λ2关系如图所示。

针对第一种情况,我们可以看出来λ2范围是(0,t−λ2+λ1),第二种情况的范围是(λ2−λ1,t)。这里我们把k又表示回了λ1, λ2,由于我们要通过迭代的方法来优化λ1, λ2的取值,所以我们令上一轮的λ1, λ2分别是λ1o, λ2o。这里的o指的是old的意思,我们把刚才求到的结论综合一下,就可以得到λ2下一轮的下界L是max(0, λ2o−λ1o),上界H是min(t+λ2o−λ1o,t)。
同理,当λ1, λ2异号时,也有k>0与k<0两种情况讨论。
当y1=y2=1时, λ1+λ2=k,此时λ2范围为(0, λ1o+λ2o)。当k>t的时候,这时候λ2的范围为(λ1o+λ2o-t,t)。
当y1=y2==-1时,λ1+λ2=k,此时k<0,由于这个时候不满足约束条件0≤λ1, λ2≤t。所以此时没有解。将两种情况综合以下得到下界L是max(0, λ1o+λ2o-t),上界是 min(λ1o+λ2o,t)。具体关系如下图:

现在假设通过迭代之后下一轮λ2是λ2new,unc,这里unc未经约束的意思。那么我们加上刚才的约束,可以得到:

这里的λ2new,unc是我们利用求导得到取极值时的,但问题是由于存在约束,这个值并不一定能取到。所以上述的一系列操作就是为了探讨约束存在下我们能够取到的极值情况。
我们现在已经得到了下一轮迭代之后得到的新的的取值范围,接下来要做的就是像梯度下降一样,求解出使得损失函数最小的λ1和λ2的值,由于λ1+λ2的值已经确定,所以我们求解出其中一个即可。
前面我们知道优化目标为:
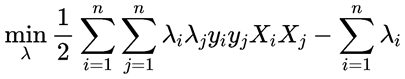


为了表示方便我们用Kij=Xi*Xj表示,将λ1和λ2作为第一轮选择的变量代入得:


我们已经知道了λ1y1+λ2y2=C,因为y1为1或者-1,所以可以得到λ1=y1(C-λ2y2)。为了进一步简化式子,令

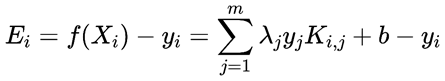
上式中,f(Xi)表示wxi+b的预测值。Ei为第i的样本预测值与实际值的差。
再代入上式化简可以得到:

然后对λ2求导求极值得到:
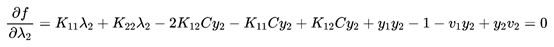
最后解得:

再根据H,L公式进行约束剪辑,得到满足约束条件的情况下最好的值,然后带入λ2求得λ1。这样就优化了一对参数,重复选择参数进行优化,知道达到迭代停止的条件(收敛或设置的阈值)为止。最后得到了所有的λ。
选择参数时,第一个参数选择不满足KKT条件的λ(尽量选择违反KKT最严重的样本),因为原问题的解的最优解是该点满足KKT条件的充分必要条件。第二参数选择能使目标函数增长最快的变量,一般选择两变量所对应样本间隔最大的点为第二个参数,或者寻找能使第二个参数足够大的变化,也就是|E1-E2|最大。然后带入之前求偏导时的式子:

可以求得W’。通过前面我们已经知道了λi>0对应的点都是支持向量,随便找一个支持向量带入边界方程可以得到:
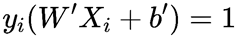
两边同时乘以yi然后求出b’即可。

为了更具有鲁棒性,可以求得支持向量的b’的平均值。 这样我们就得到了最大间隔超平面。
最后用f(x)表示预测模型的超平面,则可以表示如下:
**10. **硬间隔代码实现
由于SVM过程比较复杂,直接实现难度大,可以考虑python的sklearn库实现。

import numpy as np
from sklearn.svm import LinearSVC
import matplotlib.pyplot as plt
import matplotlib as mpl
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn import svm
from sklearn.metrics import accuracy_score
def npz_read(file_dir):
npz = np.load(file_dir)
data = npz['data']
label_list = npz['label']
npz.close()
return data, label_list
def split_train_test(data, label_list):
xtrain, xtest, ytrain, ytest = train_test_split(data, label_list, test_size=0.3)
return xtrain, xtest, ytrain, ytest
if __name__ == '__main__':
file_name = r'分布1.npz'
data, label_list = npz_read(file_name)
xtrain, xtest, ytrain, ytest = split_train_test(data, label_list)
# 线性核处理
# linear_svm = svm.LinearSVC(C=0.5, class_weight='balanced')线性问题,效率比svm.SVC高
linear_svm = svm.SVC(kernel='linear',C=10)#核函数使用线性核,相当于没有使用核函数,参数C越大,对分类要求越严,越接近硬间隔
fig=plt.figure()
ax=fig.add_subplot(111)
ax.set_xlabel("X1", color='r', fontsize=12,loc='right')
ax.set_ylabel("X2", color='r', fontsize=12,loc='top',rotation=0,labelpad=-10)
cm_dark=mpl.colors.ListedColormap(['g','r'])
ax.scatter(np.array(xtrain)[:,0],np.array(xtrain)[:,1],c=np.array(ytrain).squeeze(),cmap=cm_dark,s=30)
linear_svm.fit(xtrain, ytrain)
b = linear_svm.intercept_
print(b)
w = linear_svm.coef_
print(w)
x = np.linspace(-5, 5) # 从 -5 到 5 产生一些连续的值(随机的)
y= - (w[0][0]) / w[0][1]*x-(b/w[0][1]) # 带入 x 的值,,转换为点斜式,获得直线(超平面)方程
ax.plot(x, y, 'k-')
#超平面上下界方程为WX+b=正负1
yup= - (w[0][0]) / w[0][1]*x-(b/w[0][1])+(1/w[0][1]) # 带入 x 的值,,转换为点斜式,获得直线(超平面)方程
ydown=- (w[0][0]) / w[0][1]*x-(b/w[0][1])-(1/w[0][1])
ax.plot(x, yup, 'k--')
ax.plot(x, ydown, 'k--')
y_pred = linear_svm.predict(xtest)
print('测试集y',ytest )
print('预测y',y_pred)
print("支持向量索引: ", linear_svm.support_)
print("支持向量: ", linear_svm.support_vectors_)
print("支持向量的lamada的值:", linear_svm.dual_coef_)
print("超平面方程为:"+str(round(w[0][0],2))+"x1"+"+"+str(round(w[0][1],2))+"x2"+"+"+str(round(b[0],2))+"=0")
print('线性核的准确率为:{}'.format(accuracy_score(y_pred=y_pred, y_true=ytest)))
plt.show()



**11. **软间隔
为了避免过拟合以及数据中存在的’噪声’数据对模型的影响,又有了软间隔方法,也就是允许在原有的目标函数的基础添加一个loss函数,允许少数样本被错误分类。下图是一个更直观的理解:

上面图是完全线性可分的,当存在某些样本不满足线性可分时,就须使用软间隔来解决此类问题了。对于每一个训练样本(Xi,yi)我们都引入一个松弛变量ξi≥0,对于不满足yi(WXi+b)≥1(上下边界两侧)的样本,通过加上一个松弛变量后,使其满足yi(WXi+b)+ξi≥1,即让软间隔最大化。加入松弛变量后,我们希望间隔尽可能大的同时,又希望训练样本误分类的样本点个数尽可能少,对于样本中分类错误的我们定义一个损失为loss,则目标优化函数可以写为:

上式子中为了方便,W就相当于前面的W’了。对于损失函数,为了方便求解,我们通常希望具有凸函数且连续可导的性质, 这里通常采用hinge损失函数(中文翻译为合页损失函数)。
hinge损失:L(z)=max(0,1-z)
当z在上下界两侧时候,z是大于等于1的,此时,损失为0,否则损失为1-z。加上hinge损失函数后的目标优化函数为:

C为为惩罚系数,用来控制间隔和松弛变量惩罚的平衡,需要根据实际情况调节,当C无穷大时,上式为了满足约束就变成了硬间隔的目标优化函数(没有后面的那一项了)。我们知道yi(WXi+b)+ξi≥1,引入松弛变量ξi(ξi≥0)后,可以将目标优化函数重新变换为下式:

约束条件为


构造拉格朗日函数如下:
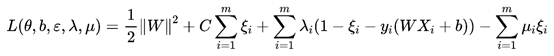
其中μi≥0, λi≥0是拉格朗日乘子。对W,b, ξi分别求偏导得到:

将上式带入拉格朗日式子得到的对偶问题如下:

约束条件:
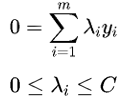
与前面的硬间隔对比可以知道,前者λi≥0,后者多了个C。软间隔SVM的KKT条件为:

参数的求解仍然可以通过前面额SMO算法求解。
通过以上KKT条件,我们知道任意的Xi,yi,总有λi=0或yi(WXi+b)+ ξi-1=0。对于每个加入软间隔的样本,到自己类别的最大间隔边界(支持向量所在的边界)距离为ξi**/**||W||。
若λi=0,则表示该样本不会对最后求得的超平面有影响。
若C>λi>0,则0<μi<C,可以得到ξi=0,表明该样本为支持向量,在最大间隔边界上。
若λi=C,则μi=0,此时若0≤ξi<1,则该样本落在自己真实类一边的最大间隔与分割超平面之间,样本被正确分类(如上个图中夹在虚线与实线中的两个绿色点)。
若λi=C,则μi=0,此时若ξi=1,则该样本落在分割超平面上,此时无法判断其属于哪一类。
若λi=C,则μi=0,此时若ξi>1,则该样本落在自己真实类的另一边,被错误分类了。
由此可以看出,软间隔支持向量机的最终模型也只与支持向量有关。
**12. **软间隔SVM代码实现
与硬间隔代码几乎一样,只需要将前面的参数C改小一点,另外使用线性不可分的数据,其他不变。

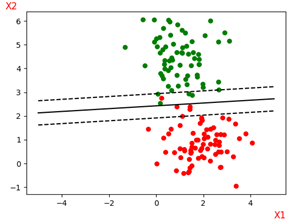
13. 线性不可分与核函数
如果数据集完全线性不可分,且使用软间隔模型准确率很低,就要考虑其他办法。比如下面两个图中(借鉴网上的)

左边样本点有蓝色和红色两个类,无法线性可分,经过变换后到高维空间后,图中任意一个样本点经过变换,使得原本在平面中变到了三维空间中可以找到一个平面将其线性分割。也就是说我们的预测模型f(x)=WX+b,要经过某种变换,假设该映射为Ф(X),则新的SVM模型预测模型为:
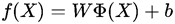
我们将变换Ф(X)带入到目标函数对偶问题中得到:

映射的维数越高,Ф(Xi)Ф(Xj)越困难,现在假设有一个函数满足:
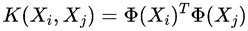
那么此时的K(Xi,Xj)就称作核函数。对偶目标函数则如下:

求解后可以得到

哪样的可以作为核函数呢?这里有个定理(mercer定理),当核矩阵(此处不作讲解)半正定时,k可以作为核函数。此时,总能找到一个与之对应的映射Ф。
有了这个之后,选取合适的核函数至关重要,若核函数选择不佳,将样本映射到不合适的特征空间,会导致模型性能不佳。以下给出常见的核函数:

简单介绍上述核函数及优缺点:
** 线性核**:只能解决线性可分问题,简单易用,可解释性强。
** 多项式核**:依靠升维使得原本线性不可分的数据线性可分。可以解决某些非线性问题,幂数太大不适用。
** 高斯核**:也叫RBF核,或径向基核,函数可以映射到无限维(可用泰勒级数展开至无限维),只有一个参数。容易过拟合,可解释性差,计算速度比较慢。
** 拉普拉斯核**:拉普拉斯核彻底等价于指数核,惟一的区别在于前者对参数的敏感性下降,也是一种径向基核函数。
** Sigmoid核**:也叫双曲正切核,采用Sigmoid函数作为核函数时,支持向量机实现的就是一种多层感知器神经网络。
常见的核函数有很多,还包括对数核、柯西核、卡方核、Wave Kernel(适用于语音处理场景)、Spherical Kernel等。另外核函数可以通过线性组合,直积等方式得到的仍然是核函数。
下面举一个使用核函数的例子:
现在有下面的样本数据分布,属于完全非线性的不可分。
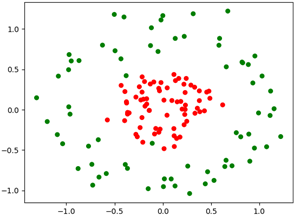
如果不使用核函数或者使用线性核函数不能够很好的划分的,就如下图这样,测试集上的准确率很低,才0.6左右。
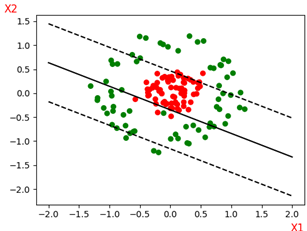
我们可以思考任意一个样本点(Xi,Xj)若果经过映射或者核函数变换从二维平面变换到三维空间,就有可能找到一个超平面划分了。
现在先使用高斯核函数来看看分类情况,在scikit-learn库中的高斯核为:
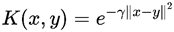
其中γ值为高斯函数sigama的倒数,其值越大,高斯分布越窄,模型越倾向过拟合,γ值越小越倾向欠拟合。现在先来看下高斯函数的样子:

现在我们可以用高斯核将样本数据映射到三维空间。俯视图中的每个同心圆构成一个平面,图中的平面正好将两类数据进行线性划分。

代码实现:

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC, SVC
import matplotlib.pyplot as plt
import matplotlib as mpl
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
def npz_read(file_dir):
npz = np.load(file_dir)
data = npz['data']
label_list = npz['label']
npz.close()
return data, label_list
def split_train_test(data, label_list):
xtrain, xtest, ytrain, ytest = train_test_split(data, label_list, test_size=0.3)
return xtrain, xtest, ytrain, ytest
def RBFKernelSVC(gamma = 1.0):
return Pipeline([("std_scaler", StandardScaler()),("svc", SVC(kernel="rbf", gamma=gamma))])
def plot_decision_boundary(model, axis):
# meshgrid函数用两个坐标轴上的点在平面上画格,返回坐标矩阵
X0, X1 = np.meshgrid(
# 随机两组数,起始值和密度由坐标轴的起始值决定
np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
)
X_grid_matrix = np.c_[X0.ravel(), X1.ravel()]
y_predict = model.predict(X_grid_matrix)
y_predict_matrix = y_predict.reshape(X0.shape)
# 设置色彩表
from matplotlib.colors import ListedColormap
my_colormap = ListedColormap(['#B0E0E6', '#FFFFCD', '#BDFCC9'])
# 绘制等高线,并且填充等高区域的颜色
plt.contourf(X0, X1, y_predict_matrix, linewidth=10, cmap=my_colormap)
if __name__ == '__main__':
file_name = r'环形分布7.npz'
data, label_list = npz_read(file_name)
xtrain, xtest, ytrain, ytest = split_train_test(data, label_list)
rbf_svc = RBFKernelSVC(gamma=10)
rbf_svc.fit(xtrain, ytrain)
plot_decision_boundary(rbf_svc, axis=[-2, 2, -2, 2])
cm_dark = mpl.colors.ListedColormap(['g', 'r'])
plt.scatter(np.array(xtrain)[:,0],np.array(xtrain)[:,1],c=np.array(ytrain).squeeze(),cmap=cm_dark,s=30)
plt.show()
y_pred = rbf_svc.predict(xtest)
print('高斯核的准确率为:{}'.format(accuracy_score(y_pred=y_pred, y_true=ytest)))

下图为绘制的等高线决策边界:

若将γ(gamma)值调大,模型更加拟合,也就是样本点的高斯分布图变多了,许多个高斯分布图重叠的区域就形成了决策区域与决策边界。
14. SVM****应用
前面提到过SVM应用于文本分类、字符识别、图像识别、人脸识别等。下面介绍几个简单的应用。
SVM癌症预测分类:
数据集为美国威斯康星州医疗人员采集了患者乳腺肿块经过细针穿刺 (FNA) 后的数字化图像,通过图像特征提取,将肿瘤肿瘤分成良性和恶性。通过相关性热力图可以选择与分类标签相关性强的特征,当特征与特征之间相关性强时,可以其中选择一个,尽可能让特征少,避免过拟合。
代码实现:

#!/usr/bin/env python
# coding: utf-8
import os
import pandas as pd
from svm_kernel_环形数据 import RBFKernelSVC
column = ['Sample code number', 'Clump Thickness', 'Uniformity of Cell Size', 'Uniformity of Cell Shape',
'Marginal Adhesion', 'Single Epithelial Cell Size', 'Bare Nuclei', 'Bland Chromatin', 'Normal Nucleoli',
'Mitoses', 'Class']
# 加载数据集
data = pd.read_csv('breast-cancer-wisconsin.data',names=column)
# id列删除
data.drop(['Sample code number'], axis=1, inplace=True) # axis参数默认为0,为1表示删除列
features_remain = [
'Uniformity of Cell Shape',
'Bland Chromatin'
]
# - 特征字段筛选,观测各变量之间的关系,使用DataFrame的corr函数,然后用热力图可视化呈现
# 将肿瘤诊断结果可视化
import seaborn as sns
import matplotlib.pyplot as plt
# 用热力图呈现字段之间的相关性
corr = data[column[1:]].corr()
plt.figure(figsize=(5,5))
sns.heatmap(corr, cmap="Purples", annot=True)
plt.show()
"""
- 颜色越深代表相关性约大,选择相关性大的作为特征,若特征之间有较强相关性,选择其中一个代表即可,特征选择的目的是降维,用少量的特征代表数据的特性,这样可以增强分类器的泛化能力,避免数据过拟合。
"""
# # 特征选择
# 准备训练集和测试集
# 抽取30%的数据作为测试集,其余作为训练集
from sklearn.model_selection import train_test_split
train,test = train_test_split(data, test_size=0.3)
train_y = train['Class']
test_y = test['Class']
train_x = train[features_remain]
test_x = test[features_remain]
# - 数据规范,为了数据在同一个量级上,避免维度问题造成数据误差,这里采用Z-Score规范化数据,保证每个特征维度的数据均值为0,方差为1
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
train_x_scaler = scaler.fit_transform(train_x)
test_x_scaler = scaler.transform(test_x)
# 建模(训练和预测)
# - SVM分类器
from sklearn import svm
from sklearn.metrics import accuracy_score
linearsvc_model = svm.SVC(kernel='linear',C=1)
linearsvc_model.fit(train_x_scaler, train_y)
prediction = linearsvc_model.predict(test_x_scaler)
print(f"线性核测试集准确率: {accuracy_score(test_y, prediction)}")#0.938
rbf_svc = RBFKernelSVC(gamma=10)
rbf_svc.fit(train_x_scaler, train_y)
prediction = rbf_svc.predict(test_x_scaler)
print(f"高斯核测试集准确率: {accuracy_score(test_y, prediction)}")#0.928


15. SVM****多分类
这里简单介绍关于多分类,有几种思路。
第一种是一对多法(one-versus-rest,OVR)
假如我有四类要划分(也就是4个label),他们是A、B、C、D。于是我在抽取训练集的时候,分别抽取
(1)A所对应的向量作为正集,B,C,D所对应的向量作为负集;
(2)B所对应的向量作为正集,A,C,D所对应的向量作为负集;
(3)C所对应的向量作为正集,A,B,D所对应的向量作为负集;
(4)D所对应的向量作为正集,A,B,C所对应的向量作为负集;
测试时,将样本用这4个分类器去分类预测,结果为正集的那个就是我们要的预测结果。其缺点是数据不均衡时,不适用。
一对多还可以使用基于决策树的SVM,这里不作介绍。
第二种是一对一法(one-versus-one)
其做法是在任意两类样本之间设计一个SVM,因此 k kk 个类别的样本就需要设计 k ( k − 1 ) / 2 k(k-1)/2k(k−1)/2 个SVM。当对一个未知样本进行分类时,最后得票最多的类别即为该未知样本的类别,这种策略称为投票法。
假设有四类A,B,C,D四类。在训练的时候我们选择(A,B)、 (A,C)、(A,D)、(B,C)、(B,D)、(C,D)所对应的向量作为训练集,然后得到六个训练结果,在测试的时候,把对应的向量分别对六个结果进行测试,然后采取投票形式,最后得到一组结果。当类别很多时,模型的个数很大,代价很大。
SVM鸢尾花预测分类
Iris数据集是常用的分类实验数据集,由Fisher, 1936收集整理。Iris也称鸢尾花卉数据集,是一类多重变量分析的数据集。数据集包含150个数据样本,分为3类,每类50个数据,每个数据包含4个属性。可通过花萼长度,花萼宽度,花瓣长度,花瓣宽度4个属性预测鸢尾花卉属于(Setosa,Versicolour,Virginica)三个种类中的哪一类。
该数据集包含了4个属性:
Sepal.Length(花萼长度),单位是cm;
Sepal.Width(花萼宽度),单位是cm;
Petal.Length(花瓣长度),单位是cm;
Petal.Width(花瓣宽度),单位是cm;
种类:Iris Setosa(山鸢尾)、Iris Versicolour(杂色鸢尾),以及Iris Virginica(维吉尼亚鸢尾)。
SVM鸢尾花多分类代码:

import numpy as np
from sklearn import svm
from sklearn import model_selection
import matplotlib.pyplot as plt
import matplotlib as mpl
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
file_path = "Iris.data"
# 该方法可将输入的字符串作为字典it 的键进行查询,输出对应的值
# 该方法就是相当于一个转换器,将数据中非浮点类型的字符串转化为浮点
def iris_type(s):
it = {b'Iris-setosa':0, b'Iris-versicolor':1, b'Iris-virginica':2}
return it[s]
# 加载data文件,类型为浮点,分隔符为逗号,对第四列也就是data 中的鸢尾花类别这一列的字符串转换为0-2 的浮点数
data = np.loadtxt(file_path, dtype=float, delimiter=',', converters={4:iris_type})
# 对data 矩阵进行分割,从第四列包括第四列开始后续所有列进行拆分
x, y = np.split(data, (4,), axis=1)
# 对x 矩阵进行切片,所有行都取,但只取前两列
x = x[:, 0:2]
print(x)
# 随机分配训练数据和测试数据,随机数种子为1,测试数据占比为0.3
data_train, data_test, tag_train, tag_test = model_selection.train_test_split(x, y, random_state=1, test_size=0.3)
#=============== 模型搭建 ===============
def classifier():
clf = svm.SVC(C=0.5, # 误差惩罚系数,默认1
kernel='linear', # 线性核 kenrel='rbf':高斯核
decision_function_shape='ovr') # OVR一对多决策函数
return clf
# 定义SVM(支持向量机)模型
clf = classifier()
#=============== 模型训练 ===============
def train(clf, x_train, y_train):
clf.fit(x_train, # 训练集特征向量
y_train.ravel()) # 训练集目标值
# 训练SVM 模型
train(clf, data_train, tag_train)
#=============== 模型评估 ===============
def show_accuracy(a, b, tip):
acc = a.ravel() == b.ravel()
print('%s Accuracy:%.3f' % (tip, np.mean(acc)))
def print_accuracy(clf, x_train, y_train, x_test, y_test):
# 分别打印训练集和测试集的准确率
# score(x_train, y_train):表示输出x_train, y_train 在模型上的准确率
print('training prediction:%.3f' % (clf.score(x_train, y_train)))
print('test data prediction:%.3f' % (clf.score(x_test, y_test)))
# 原始结果与预测结果进行对比
# predict() 表示对x_train 样本进行预测,返回样本类别
show_accuracy(clf.predict(x_train), y_train, 'training data')
show_accuracy(clf.predict(x_test), y_test, 'testing data')
# 计算决策函数的值,表示x到各分割平面的距离
print('decision_function:\n', clf.decision_function(x_train))
print_accuracy(clf, data_train, tag_train, data_test, tag_test)
#============== 模型可视化 ===============
def draw(clf, x):
iris_feature = 'sepal length', 'sepal width', 'petal length', 'petal width'
# 开始画图
# 第0 列的范围
x1_min, x1_max = x[:, 0].min(), x[:, 0].max()
# 第1 列的范围
x2_min, x2_max = x[:, 1].min(), x[:, 1].max()
x1, x2 = np.mgrid[x1_min:x1_max:200j, x2_min:x2_max:200j]
grid_test = np.stack((x1.flat, x2.flat), axis=1)
print('grid_test:\n', grid_test)
# 输出样本到决策面的距离
z = clf.decision_function(grid_test)
print('the distance to decision plane:\n', z)
# 预测分类值
grid_hat = clf.predict(grid_test)
print('grid_hat:\n', grid_hat)
grid_hat = grid_hat.reshape(x1.shape)
cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
plt.pcolormesh(x1, x2, grid_hat, cmap=cm_light)
# 样本点
plt.scatter(x[:, 0], x[:, 1], c=np.squeeze(y), edgecolor='k', s=50, cmap=cm_dark)
# 测试点
plt.scatter(data_test[:, 0], data_test[:, 1], s=120, facecolor='none', zorder=10)
plt.xlabel(iris_feature[0], fontsize=10)
plt.ylabel(iris_feature[1], fontsize=10)
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.title('SVM鸢尾花分类', fontsize=10)
plt.show()
draw(clf, x)


小结:本文先介绍了SVM的由来及应用领域,对SVM的原理进行了介绍,推导了一些公式,最后构造拉格朗日函数求解,由于是凸二次规划问题,转换为对偶问题求解,最后利用SMO序列化最小算法求最优解,最后举了鸢尾花与癌症的例子,本作者能力有限,未对Slater条件及hessian矩、梯度下降法求解SVM参数进行详细介绍,关于梯度下降求解参数可以参考最后一个链接。
版权归原作者 Air_IoT 所有, 如有侵权,请联系我们删除。