文章目录
前言
提示：本系列主要讲解如何用python实现常见组合优化问题中的QUBO公式：
量子退火作为解决组合优化问题的利器，车辆路径问题（VRP : Vehicle Routing Problem）是最经常被提起的现实应用。该问题的定义和特点如下：
- 车辆路径问题 (VRP) 是优化多辆送货车辆的送货顺序的组合优化问题，是旅行商问题 (TSP) 的推广。
- 这是一个可以应用于各种现实世界问题的问题，例如物流中的货物配送、工厂中的货物搬运，以及按需运输服务中的车辆分配计划。
- VRP 是一个典型的组合优化问题，也是经典的NP-Hard问题，普通计算机很难在多项式时间内找到精确解。
- 量子退火有望利用量子隧穿效应实时解决 NP-Hard 组合优化问题。
一、车辆路径问题（VRP）的QUBO建模
本章节主要参考以下论文：
齋藤和広, 大山重樹, 梅木智光, 黒川茂莉, 小野智弘, "配送計画問題への量子アニーリング適用に関する初期評価" DEIM2020 D2-4(day1 p25) https://proceedings-of-deim.github.io/DEIM2020/papers/D2-4.pdf
作为一个基本的VRP，我们考虑了当多辆运送车辆访问所有目标基地时，搜索总旅行成本最小的路线的组合优化问题。
我们假设所有的送货车辆都从一个叫做 Depot 的基地出发，并且总是在最后返回到 Depot。移动成本使用基地之间的距离计算。距离矩阵的实现如下：
- VRP的QUBO的定义： 我们把地点1作为Depot，然后假设有2辆车用来配送4个地点。2辆车的配送示意图如下：
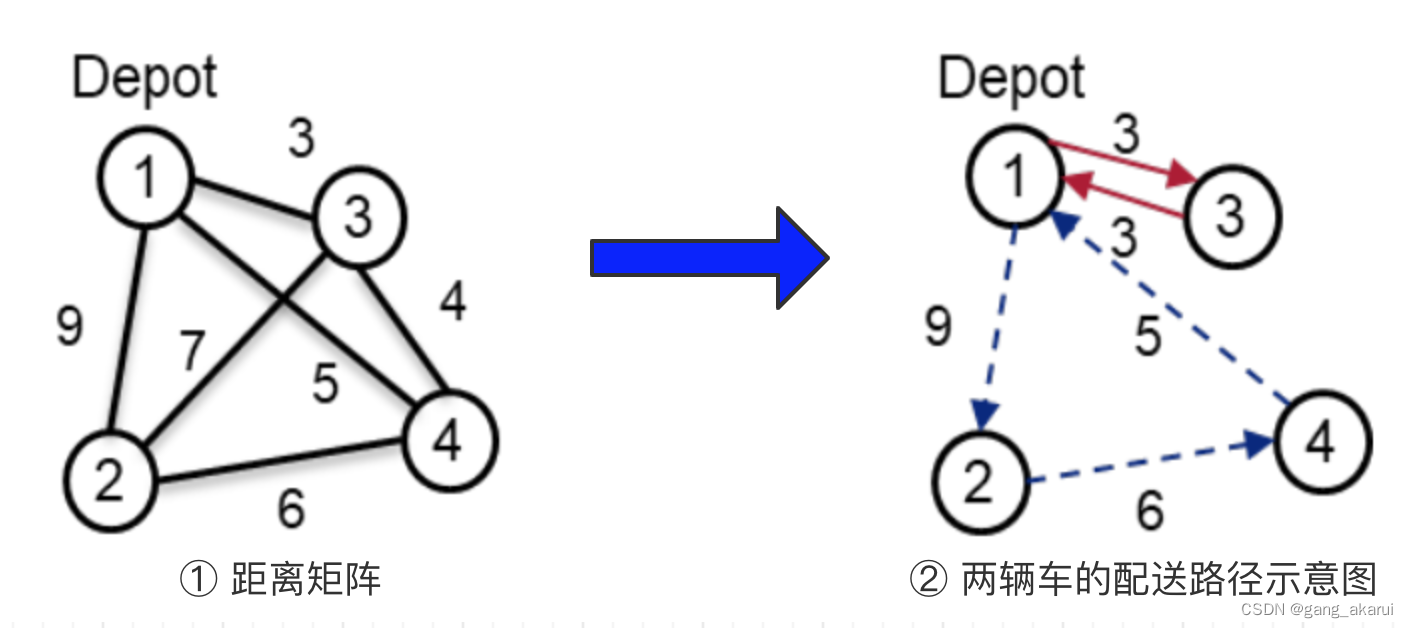
其实大家可以可以把VRP问题理解为，有V辆车，V辆车各自负责不重叠的地点子集，所有车辆负责的地点子集的路径总和最小。
所以这里我们有三个参数需要设定：
- V：车辆个数
- P：地点个数
- S：时间步（TSP建模中，我们不需要设置时间步，因为S=P+1）
小写字母代表变量：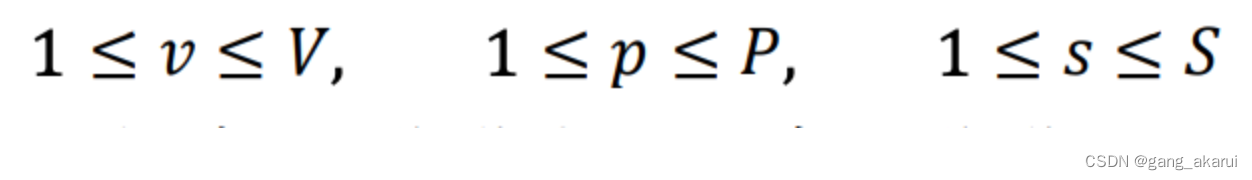
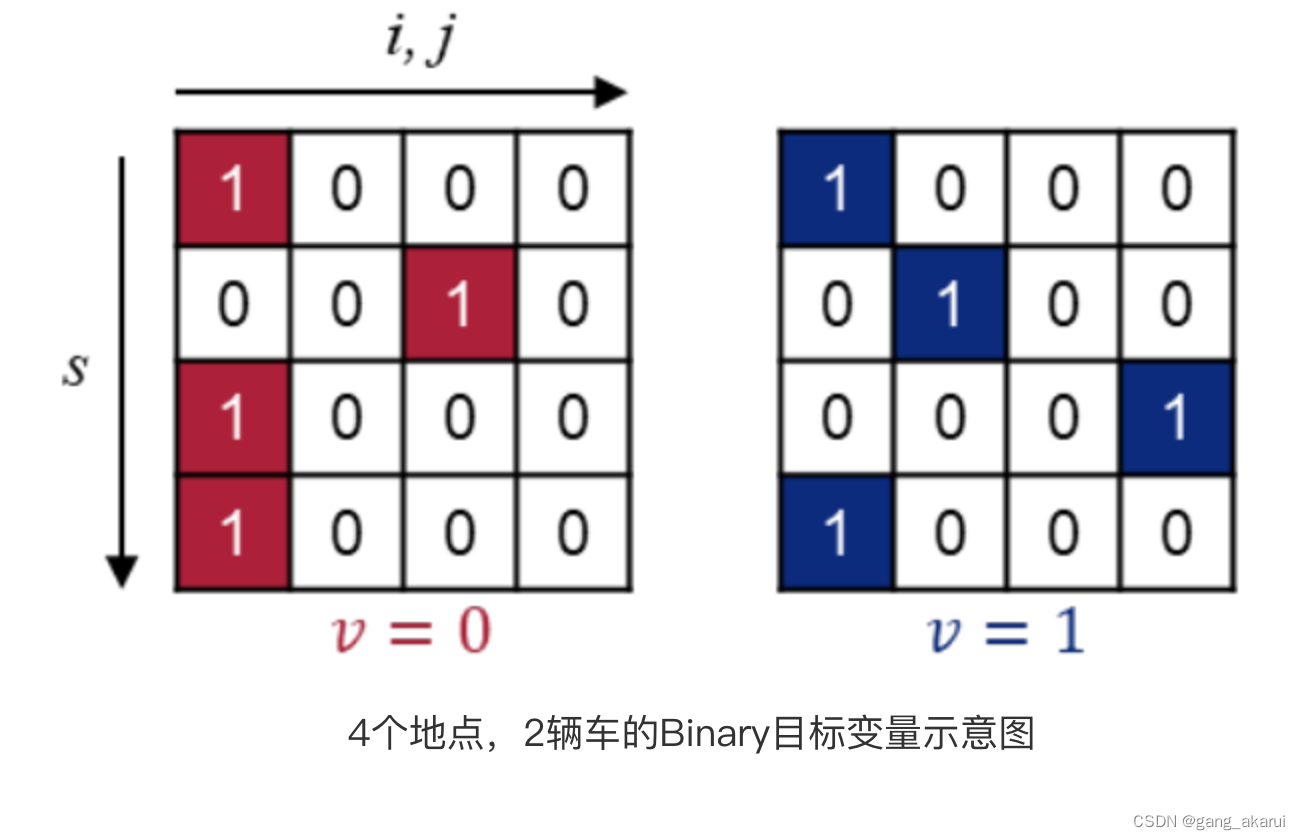
1.目标变量
目标变量如下所示：
我们期待的QUBO矩阵如下图所示，
- 红色矩阵代表车辆1，从地点1==>地点3==>地点1；
- 蓝色矩阵代表车辆2，从地点1==>地点2==>地点4==>地点1。
下面写出目标函数和约束条件：
2.目标函数定义
- 目标函数 – 其实就是TSP的目标函数，又增加了一个车辆的维度 ∑ v = 1 V \sum_{v=1}^V ∑v=1V。
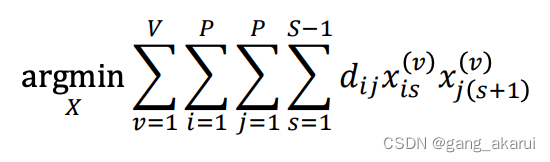
3.约束条件定义
- 约束条件 – 条件a：第1个时间步的地点必须是Depot地点 – 条件b：第S个时间步的地点必须是Depot地点 – 条件c：除了Depot地点，剩余地点必须被访问过一次 – 条件d：相同时间步，不同车辆v不能在同一地点p各个约束条件对应的表达式如下图：
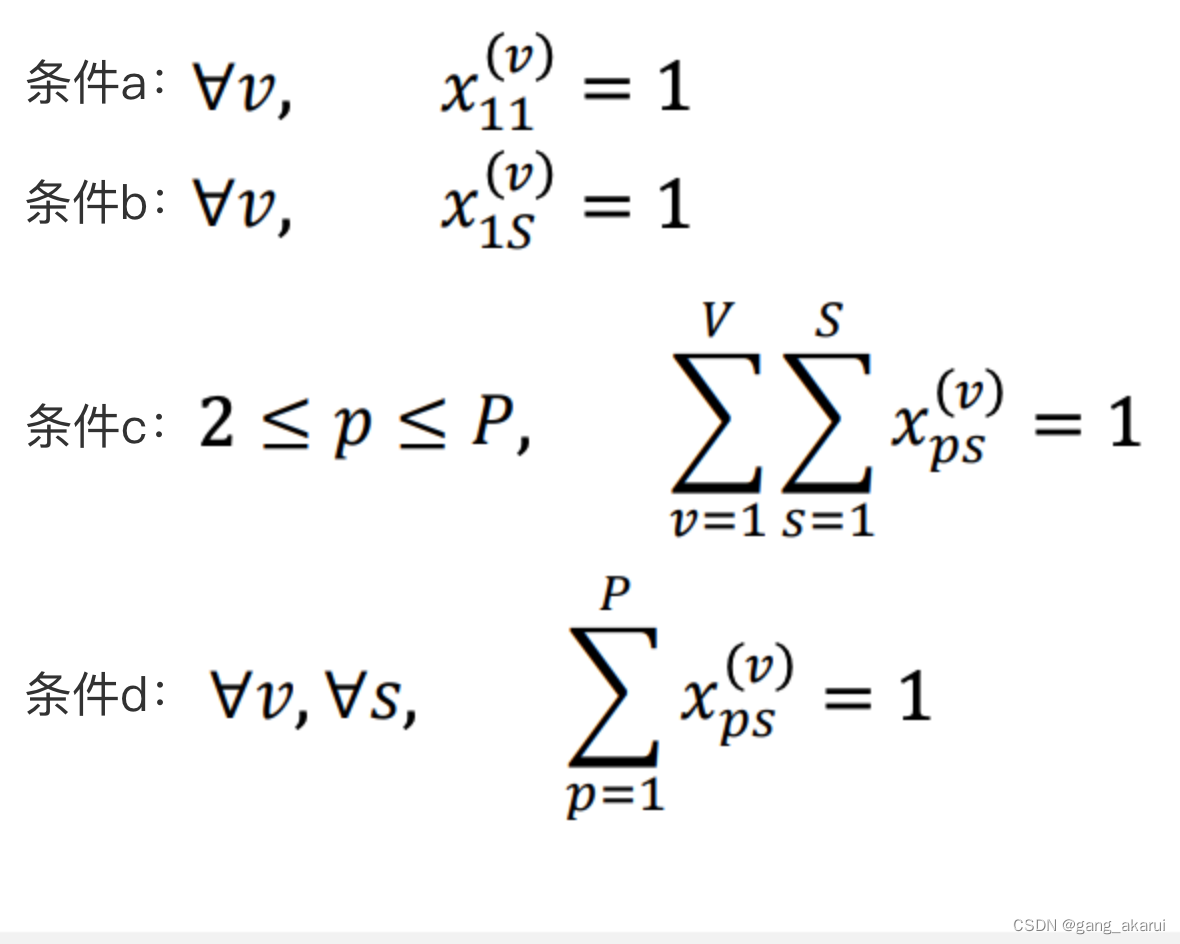最后转换后的哈密顿量 H \mathcal{H} H为: H = H o b j + w 1 H a + w 2 H b + w 3 H c + w 4 H d \mathcal{H}=\mathcal{H}_{obj}+w_1 \mathcal{H}_a+w_2 \mathcal{H}_b+w_3 \mathcal{H}_c+w_4 \mathcal{H}_d H=Hobj+w1Ha+w2Hb+w3Hc+w4HdH o b j = ∑ v = 1 V ∑ i = 1 P ∑ j = 1 P ∑ s = 1 S − 1 d i j x i s ( v ) x j ( s + 1 ) ( v ) \mathcal{H}_{obj}=\sum_{v=1}^V \sum_{i=1}^P \sum_{j=1}^P \sum_{s=1}^{S-1} d_{i j} x_{i s}^{(v)} x_{j(s+1)}^{(v)} Hobj=∑v=1V∑i=1P∑j=1P∑s=1S−1dijxis(v)xj(s+1)(v)H a = ∑ v = 1 V ( 1 − x 11 ( v ) ) 2 \mathcal{H}_a=\sum_{v=1}^V\left(1-x_{11}^{(v)}\right)^2 Ha=∑v=1V(1−x11(v))2H b = ∑ v = 1 V ( 1 − x 1 S ( v ) ) 2 \mathcal{H}_b=\sum_{v=1}^V\left(1-x_{1 S}^{(v)}\right)^2 Hb=∑v=1V(1−x1S(v))2H c = ∑ p = 2 P ( 1 − ∑ v = 1 V ∑ s = 1 S x p s ( v ) ) 2 \mathcal{H}_c=\sum_{p=2}^P\left(1-\sum_{v=1}^V \sum_{s=1}^S x_{p s}^{(v)}\right)^2 Hc=∑p=2P(1−∑v=1V∑s=1Sxps(v))2H d = ∑ v = 1 V ∑ s = 1 s ( 1 − ∑ p = 1 P x p s ( v ) ) 2 \mathcal{H}_d=\sum_{v=1}^V \sum_{s=1}^s\left(1-\sum_{p=1}^P x_{p s}^{(v)}\right)^2 Hd=∑v=1V∑s=1s(1−∑p=1Pxps(v))2
二、Python实现VRP的QUBO
本章节主要来自以下代码库：https://github.com/yskmt2018/quantum2020/blob/master/vehicle_routing_problem.ipynb
1.引入库
import math
import pyqubo
import numpy as np
import pandas as pd
from openjij import SQASampler
2.设置参数和距离矩阵
# 车辆个数
V =3
# 地点个数
L =len(distance[0])
# 最大时间步
S =10
# 距离矩阵
distance = np.array([[0,548,776,696,582,274,502,194,308,194,536,502,452,1020,393,208,1196,983,427,482,479,517],[548,0,684,308,194,502,730,354,696,742,1084,594,1102,298,741,582,712,1085,1024,202,220,1050],[776,684,0,992,878,502,274,810,468,742,400,1278,1152,819,510,514,399,537,579,509,285,555],[696,308,992,0,114,650,878,502,844,890,1232,514,300,263,593,153,801,1128,729,1230,317,946],[582,194,878,114,0,536,764,388,730,776,1118,400,511,886,168,514,396,594,886,190,729,1042],[274,502,502,650,536,0,228,308,194,240,582,776,270,343,716,535,1269,410,1177,494,1133,651],[502,730,274,878,764,228,0,536,194,468,354,1004,144,353,408,220,636,514,1180,1146,130,648],[194,354,810,502,388,308,536,0,342,388,730,468,476,1296,338,1100,1125,986,710,320,279,460],[308,696,468,844,730,194,194,342,0,274,388,810,263,138,145,740,1251,1262,402,569,189,877],[194,742,742,890,776,240,468,388,274,0,342,536,1190,757,293,580,1195,124,268,505,309,602],[536,1084,400,1232,1118,582,354,730,388,342,0,878,369,161,306,1074,1110,1130,347,163,817,637],[502,594,1278,514,400,776,1004,468,810,536,878,0,381,1041,1004,1251,406,578,1231,584,727,902],[452,1102,1152,300,511,270,144,476,263,1190,369,381,0,720,1011,991,957,233,758,934,1054,154],[1020,298,819,263,886,343,353,1296,138,757,161,1041,720,0,156,958,1202,919,401,685,716,994],[393,741,510,593,168,716,408,338,145,293,306,1004,1011,156,0,798,270,298,618,246,766,957],[208,582,514,153,514,535,220,1100,740,580,1074,1251,991,958,798,0,1244,516,710,1086,946,1098],[1196,712,399,801,396,1269,636,1125,1251,1195,1110,406,957,1202,270,1244,0,1112,1031,1106,785,913],[983,1085,537,1128,594,410,514,986,1262,124,1130,578,233,919,298,516,1112,0,593,109,649,1150],[427,1024,579,729,886,1177,1180,710,402,268,347,1231,758,401,618,710,1031,593,0,676,785,602],[482,202,509,1230,190,494,1146,320,569,505,163,584,934,685,246,1086,1106,109,676,0,394,263],[479,220,285,317,729,1133,130,279,189,309,817,727,1054,716,766,946,785,649,785,394,0,826],[517,1050,555,946,1042,651,648,460,877,602,637,902,154,994,957,1098,913,1150,602,263,826,0],])
3.QUBO实现
H o b j = ∑ v = 1 V ∑ i = 1 P ∑ j = 1 P ∑ s = 1 S − 1 d i j x i s ( v ) x j ( s + 1 ) ( v ) \mathcal{H}_{obj}=\sum_{v=1}^V \sum_{i=1}^P \sum_{j=1}^P \sum_{s=1}^{S-1} d_{i j} x_{i s}^{(v)} x_{j(s+1)}^{(v)} Hobj=∑v=1V∑i=1P∑j=1P∑s=1S−1dijxis(v)xj(s+1)(v)
defbuild_objective(x: pyqubo.array.Array)-> pyqubo.core.express.AddList:
H =sum(distance[l_from][l_to]* x[v][s][l_from]* x[v][s+1][l_to]for v inrange(V)for s inrange(S-1)for l_from inrange(L)for l_to inrange(L))return H
H a = ∑ v = 1 V ( 1 − x 11 ( v ) ) 2 \mathcal{H}_a=\sum_{v=1}^V\left(1-x_{11}^{(v)}\right)^2 Ha=∑v=1V(1−x11(v))2
defbuild_depot_start_rule(x: pyqubo.array.Array)-> pyqubo.core.express.Constraint:
H = pyqubo.Constraint(sum((x[v][0][0]-1)**2for v inrange(V)),'w_0')return H
H b = ∑ v = 1 V ( 1 − x 1 S ( v ) ) 2 \mathcal{H}_b=\sum_{v=1}^V\left(1-x_{1 S}^{(v)}\right)^2 Hb=∑v=1V(1−x1S(v))2
defbuild_depot_end_rule(x: pyqubo.array.Array)-> pyqubo.core.express.Constraint:
H = pyqubo.Constraint(sum((x[v][S-1][0]-1)**2for v inrange(V)),'w_1')return H
H c = ∑ p = 2 P ( 1 − ∑ v = 1 V ∑ s = 1 S x p s ( v ) ) 2 \mathcal{H}_c=\sum_{p=2}^P\left(1-\sum_{v=1}^V \sum_{s=1}^S x_{p s}^{(v)}\right)^2 Hc=∑p=2P(1−∑v=1V∑s=1Sxps(v))2
defbuild_vehicle_stay_rule(x: pyqubo.array.Array)-> pyqubo.core.express.Constraint:
H = pyqubo.Constraint(sum((sum(x[v][s][l]for l inrange(L))-1)**2for v inrange(V)for s inrange(S)),'w_2')return H
H d = ∑ v = 1 V ∑ s = 1 s ( 1 − ∑ p = 1 P x p s ( v ) ) 2 \mathcal{H}_d=\sum_{v=1}^V \sum_{s=1}^s\left(1-\sum_{p=1}^P x_{p s}^{(v)}\right)^2 Hd=∑v=1V∑s=1s(1−∑p=1Pxps(v))2
defbuild_location_visit_rule(x: pyqubo.array.Array)-> pyqubo.core.express.Constraint:
H = pyqubo.Constraint(sum((sum(x[v][s][l]for v inrange(V)for s inrange(S))-1)**2for l inrange(1, L)),'w_3')return H
H = H o b j + w 1 H a + w 2 H b + w 3 H c + w 4 H d \mathcal{H}=\mathcal{H}_{obj}+w_1 \mathcal{H}_a+w_2 \mathcal{H}_b+w_3 \mathcal{H}_c+w_4 \mathcal{H}_d H=Hobj+w1Ha+w2Hb+w3Hc+w4Hd
# Vehicle Routing
x = pyqubo.Array.create('x', shape=(V,S,L), vartype='BINARY')%%time
H = build_objective(x)+ \
pyqubo.Placeholder('w_1')* build_depot_start_rule(x)+ \
pyqubo.Placeholder('w_2')* build_depot_end_rule(x)+ \
pyqubo.Placeholder('w_3')* build_vehicle_stay_rule(x)+ \
pyqubo.Placeholder('w_4')* build_location_visit_rule(x)
feed_dict ={'w_1':1000,'w_2':1000,'w_3':1000,'w_4':1000}
model = H.compile()
qubo, constant = model.to_qubo(feed_dict=feed_dict)
4.OpenJij求解QUBO目标变量
OpenJij（GitHub链接）是使用普通计算机提供SQA（Simulated Quantum Annealing）API来求解，经常用来搭配OpenJij使用。
sampler = SQASampler(trotter=20, num_reads=10)
response = sampler.sample_qubo(qubo)
5.输出求解结果路径
defextract_samples(response)->(list,list):
solutions =[]
energies =[]for record in response.record:
sol, num_occ = record[0], record[2]
solution, broken, energy = model.decode_solution(dict(zip(response.variables, sol)), vartype='BINARY', feed_dict=feed_dict)iflen(broken)==0:
solutions +=[solution]* num_occ
energies +=[energy]* num_occ
return solutions, energies
solutions, energies = extract_samples(response)defvehicle_movement(solution:list)->list:
vehicles =[]for v inrange(V):
solution_sorted =sorted(solution['x'][v].items(), key=lambda x:x[0])
s =[i[1]for i in solution_sorted]
df = pd.DataFrame(s).astype(int)
df.columns =[chr(l)for l inrange(65,65+L)]
vehicles.append(df)return vehicles
best_solution = solutions[energies.index(min(energies))]
best_vehicles = vehicle_movement(best_solution)defhighlight_positive(val:int)->str:if val ==1:return'color: {}; font-weight: bold'.format('red')else:return'color: {}'.format('gray')for v inrange(V):
display_html('<b>vehicle-{}</b>'.format(v+1)+ best_vehicles[v].style.applymap(highlight_positive)._repr_html_()+'<br>', raw=True)
最后的输出结果如下：
总结
本文讲解以最短距离为优化目标的VRP的求解，约束条件也比较简单，真正的应用里，也有以最短时间为优化目标的，也有很多考率以下约束条件的：
- 优先送货服务
- 车辆载货量有限制
- 指定时间配送
至于建模以上类似的约束条件，下面两篇文章可以给大家一些启示：
- A Hybrid Solution Method for the Capacitated Vehicle Routing Problem Using a Quantum Annealer https://arxiv.org/abs/1811.07403
- Quantum Annealing of Vehicle Routing Problem with Time, State and Capacity https://arxiv.org/abs/1903.06322
下一篇讲解，护士工作时间排班问题。
本文转载自: https://blog.csdn.net/gangshen1993/article/details/128164636
版权归原作者 gang_akarui 所有， 如有侵权，请联系我们删除。
版权归原作者 gang_akarui 所有， 如有侵权，请联系我们删除。