0
0

KAN专家混合模型在高性能时间序列预测中的应用：RMoK模型架构探析与Python代码实验

Kolmogorov-Arnold网络（KAN）的提出为深度学习领域带来了重要突破，它作为多层感知器（MLP）的一种替代方案，展现了新的可能性。MLP作为众多深度学习模型的基础构件，包括目前最先进的预测方法如N-BEATS、NHiTS和TSMixer，已经在各个领域得到广泛应用。

但是我们在使用KAN、MLP、NHiTS和NBEATS进行的预测基准测试中发现，KAN在各种预测任务中表现出较低的效率和准确性。这项基准测试使用了M3和M4数据集，涵盖了超过99,000个独特的时间序列，频率范围从每小时到每年不等。这些结果表明，KAN在时间序列预测领域的应用前景并不乐观。

近期，随着论文《KAN4TSF: KAN和基于KAN的模型对时间序列预测有效吗？》中引入的可逆KAN混合模型（Reversible Mixture of KAN, RMoK）号称能够提高KAN的性能。本文将深入探讨RMoK模型的架构和内部机制，并通过Python实现一个小型实验来验证其性能。

为了全面理解本研究，建议读者参考原始论文以获取更详细的信息（本文最后的参考附带所有内容链接）。

KAN模型回顾

在深入RMoK架构之前，我们首先回顾KAN的基本原理和工作机制。

图1MLP与KAN的比较：MLP在连接上具有可学习的权重，节点上有固定的激活函数。KAN在连接上使用可学习的激活函数，节点执行求和操作。

上图展示了MLP和KAN的核心差异。在MLP中连接代表可学习的权重，节点是固定的激活函数（如ReLU、tanh等）。而KAN采用了不同的方法，在连接上使用可学习的激活函数，节点则执行这些函数的求和操作。

这种设计体现了Kolmogorov-Arnold表示定理，该定理指出多元函数可以通过单变量函数的组合来表示。具体而言，KAN使用B样条作为可学习函数来模拟非线性数据，如图2所示。这种方法为模型提供了极大的灵活性，使其能够学习复杂的非线性关系。

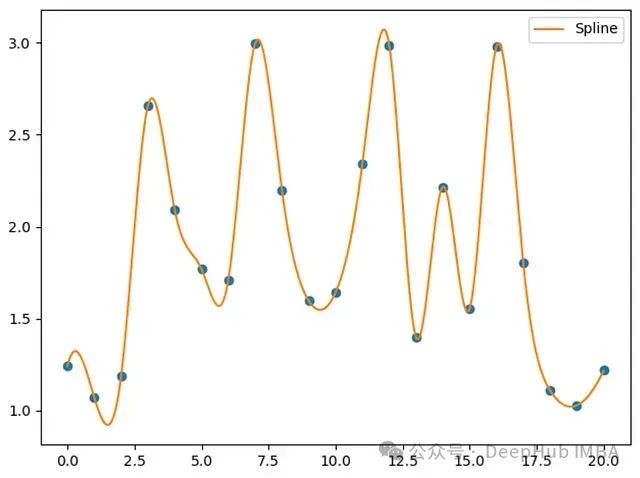
图2：三次样条拟合非线性数据示例。

尽管样条函数具有很强的灵活性，研究人员仍然提出了多种KAN变体，以进一步扩展其应用范围和提高性能。其中，Wav-KAN、JacobiKAN和TaylorKAN是RMoK模型中采用的三种重要变体。

Wav-KAN

Wav-KAN使用小波函数代替样条函数。小波函数在处理信号（如时间序列）时特别有效，因为它们能同时提取频率和位置信息。

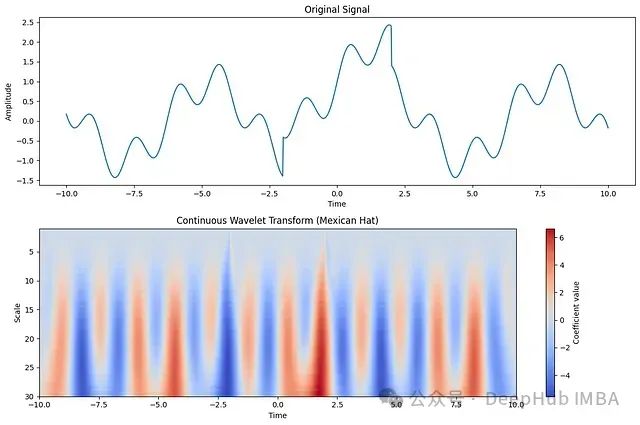
图3：使用Ricker小波（又称墨西哥帽小波）对信号进行变换的示例。

图3展示了Ricker小波如何将输入信号转换。下图中的振荡变化反映了原始信号的特征，而在-2.5和2.5标记附近的深色区域则表示原始信号的突变。这种特性使Wav-KAN特别适合处理时间序列数据，能够有效捕捉位置和频率的变化。

JacobiKAN和TaylorKAN

除了样条函数，雅可比多项式和泰勒多项式也是常用的函数近似方法，分别导致了JacobiKAN和TaylorKAN的开发。

TaylorKAN

泰勒多项式是函数在展开点处导数的无限和的近似。展开点是函数和其近似的导数相等的位置。

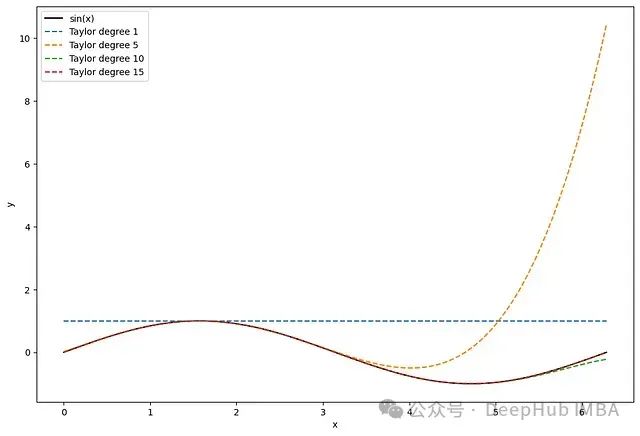
图4：使用泰勒多项式近似sin(x)函数。随着多项式阶数增加，近似效果逐渐改善。

图4展示了使用不同阶数的泰勒多项式对sin(x)函数的近似，其中π/2是展开点。可以观察到，随着阶数增加，近似效果显著提升。然而，值得注意的是，当远离展开点时，近似效果会迅速下降。

JacobiKAN

雅可比多项式形成一个函数基，可以组合使用来近似更复杂的函数，类似于B样条的作用。

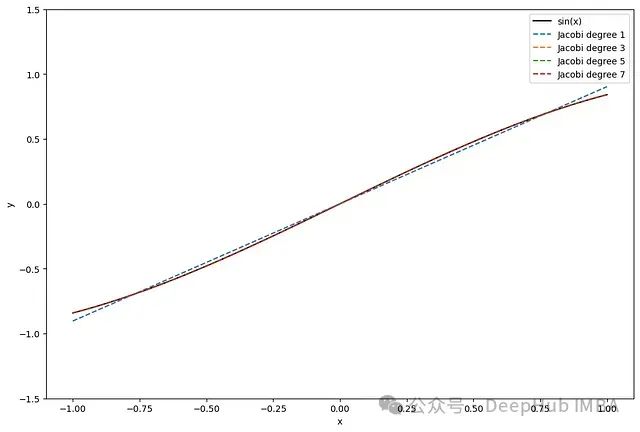
图5：使用雅可比多项式近似sin(x)函数。同样，随着多项式阶数增加，近似效果不断改善。

图5再次展示了对sin(x)函数的近似，这次使用雅可比多项式。与泰勒多项式相比，雅可比多项式在整个函数域内提供了更均衡的近似效果。

雅可比多项式更适合全局近似，其误差通常均匀分布。相比之下，泰勒多项式更适合局部近似。

综上所述，我们可以看到，将Wav-KAN用于信号处理，JacobiKAN用于准确的全局近似，以及TaylorKAN用于局部近似相结合，有可能在学习时间序列数据的复杂关系方面取得显著成效。这正是RMoK模型的核心思想。

RMoK模型架构解析

可逆KAN混合模型（Reversible Mixture of KAN, RMoK）是一种结构简洁而高效的模型，它巧妙地将门控网络与由不同专家KAN层组成的单一"KAN混合"层相结合。图6详细展示了RMoK的完整架构。

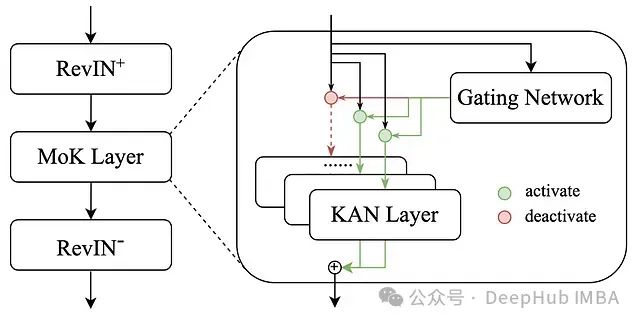
图6：RMoK模型架构示意图。

从图6中我们可以看到，RMoK模型采用了RevIN（Reversible Instance Normalization，可逆实例归一化）技术。RevIN是一种先进的预处理方法，专门用于处理非平稳时间序列数据，它显著提高了预测模型的性能。

数据流和处理流程

RMoK模型中的数据处理流程如下：

  1. 数据输入：时间序列数据从模型顶部输入。
  2. RevIN处理：数据首先通过RevIN进行归一化处理。
  3. KAN混合层：归一化后的数据进入KAN混合（MoK）层。
  4. 预测生成：MoK层输出经过反归一化处理，得到最终预测结果。

KAN混合（MoK）层

MoK层是RMoK模型的核心组件，它由以下部分组成：

  1. 门控网络：负责为数据的不同部分激活适当的专家层。
  2. 专家KAN层：包括Wav-KAN、JacobiKAN和TaylorKAN，每种专家层专注于捕捉时间序列数据的特定特征：- Wav-KAN：专门学习频率和位置特征- JacobiKAN：擅长捕捉长期变化- TaylorKAN：专注于局部短期变化的学习

门控网络的作用是动态地决定在处理数据的不同部分时应该激活哪些专家层。这种机制使得模型能够灵活地应对时间序列中的各种模式和变化。

预测生成过程

在MoK层中，每个专家层独立生成预测，然后这些预测被组合起来形成一个综合预测。这个过程发生在归一化的数据空间中。综合预测通过反归一化处理，得到最终的时间序列预测结果。

RMoK的优势

RMoK模型的设计理念虽然简洁，但其效果却非常显著。它的主要优势在于：

  1. 灵活性：通过组合不同的KAN专家层，模型能够适应各种复杂的时间序列模式。
  2. 精确性：每个专家层都专注于特定类型的特征，使得模型能够全面且精确地捕捉时间序列的各个方面。
  3. 可解释性：模型的分层结构和专家机制提高了预测结果的可解释性。

RMoK模型的核心创新在于为时间序列预测任务选择了合适的"专家"组合。Wav-KAN处理信号特征，JacobiKAN负责全局趋势，而TaylorKAN则关注局部变化，这种组合使得模型能够全面地分析和预测复杂的时间序列数据。

通过深入理解RMoK模型的架构和工作原理，我们可以更好地认识其在时间序列预测任务中的潜力。接下来将通过一个Python实验来实际验证RMoK模型的性能。

实验设计与实施

为了验证RMoK模型的有效性，我们设计了一个对比实验，将RMoK模型与其他先进的时间序列预测模型（如PatchTST、iTransformer和TSMixer）进行性能比较。本实验聚焦于长期预测任务，使用了电力变压器数据集（ETT）作为基准。

数据集介绍

本实验采用的ETT数据集是记录了中国某省两个地区的电力变压器油温数据。数据集包含四个子集，分别以每小时和每15分钟的频率采样。我们的实验专注于使用两个15分钟采样频率的数据集（ETTm1和ETTm2）。

实验环境配置

为了简化实验流程并确保结果的可复现性，我们基于官方仓库的RMoK模型实现，扩展了neuralforecast库。这使我们能够以统一的方式使用和测试不同的预测模型。

需要注意的是，在本文撰写时RMoK模型尚未被纳入neuralforecast的稳定版本。因此要复现实验结果，需要克隆特定的代码仓库分支。如果该分支已合并到主分支，可以通过以下命令安装：

 pip install git+https://github.com/Nixtla/neuralforecast.git

代码实现

1、环境准备

首先导入必要的库和模块：

 importpandasaspd  
 importnumpyasnp  
 importmatplotlib.pyplotasplt  
   
 fromdatasetsforecast.long_horizonimportLongHorizon  
   
 fromneuralforecast.coreimportNeuralForecast  
 fromneuralforecast.losses.pytorchimportMAE, MSE  
 fromneuralforecast.modelsimportTSMixer, PatchTST, iTransformer, RMoK  
   
 fromutilsforecast.lossesimportmae, mse  
 fromutilsforecast.evaluationimportevaluate

2、数据加载函数

定义了一个辅助函数来加载数据集，并设置相应的实验参数：

 defload_data(name):  
     ifname=='Ettm1':  
         Y_df, *_=LongHorizon.load(directory='./', group='ETTm1')  
         Y_df['ds'] =pd.to_datetime(Y_df['ds'])  
         freq='15T'  
         h=96  
         val_size=11520  
         test_size=11520  
     elifname=='Ettm2':  
         Y_df, *_=LongHorizon.load(directory='./', group='ETTm2')  
         Y_df['ds'] =pd.to_datetime(Y_df['ds'])  
         freq='15T'  
         h=96  
         val_size=11520  
         test_size=11520  
   
     returnY_df, h, val_size, test_size, freq

设置预测horizon为96个时间步，这相当于预测未来24小时的数据。

3、模型初始化和训练

为每个数据集初始化并训练模型：

 DATASETS= ['Ettm1', 'Ettm2']  
   
 fordatasetinDATASETS:  
     Y_df, horizon, val_size, test_size, freq=load_data(dataset)  
   
     rmok_model=RMoK(input_size=horizon,  
                       h=horizon,   
                       n_series=7,  
                       num_experts=4,  
                       dropout=0.1,  
                       revine_affine=True,  
                       learning_rate=0.001,  
                       scaler_type='identity',  
                       max_steps=1000,  
                       early_stop_patience_steps=5)
     
     # 初始化其他模型...
     
     models= [rmok_model, patchtst_model, iTransformer_model, tsmixer_model]  
   
     nf=NeuralForecast(models=models, freq=freq)
     
     # 使用交叉验证进行训练和预测
     nf_preds=nf.cross_validation(df=Y_df, val_size=val_size, test_size=test_size, n_windows=None)  
     nf_preds=nf_preds.reset_index()
     
     # 保存预测结果
     evaluation=evaluate(df=nf_preds, metrics=[mae, mse], models=['RMoK', 'PatchTST', 'iTransformer', 'TSMixer'])  
     evaluation.to_csv(f'{dataset}_results.csv', index=False, header=True)

在RMoK模型中，使用了4个专家（Wav-KAN、JacobiKAN、TaylorKAN和一个简单的MLP）。学习率设置为0.001，最大训练步数为1000，早停值为5。

4、结果评估

使用平均绝对误差（MAE）和均方误差（MSE）来评估模型性能：

 ettm1_eval=pd.read_csv('Ettm1_results.csv')  
 ettm1_eval=ettm1_eval.drop(['unique_id'], axis=1).groupby('metric').mean().reset_index()  
   
 ettm2_eval=pd.read_csv('Ettm2_results.csv')  
 ettm2_eval=ettm2_eval.drop(['unique_id'], axis=1).groupby('metric').mean().reset_index()

实验结果与分析

表1总结了各模型在ETTm1和ETTm2数据集上的性能：

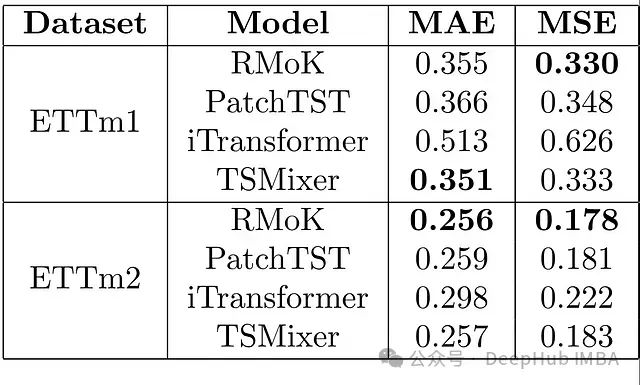
表1：不同模型在96时间步预测horizon上的性能指标。最佳结果以粗体显示。

可以观察到：

  1. 对于ETTm1数据集，RMoK模型在MSE指标上取得了最佳成绩。
  2. 在ETTm2数据集上，RMoK模型在MAE和MSE两个指标上都优于其他模型。

这些结果表明，RMoK模型在长期时间序列预测任务中展现出了强大的性能，能够与当前最先进的预测方法（如TSMixer和PatchTST）相媲美，甚至在某些情况下表现更优。

总结

本研究深入探讨了可逆KAN混合（RMoK）模型，这是一种将不同KAN专家层巧妙结合的创新模型，专门用于时间序列预测任务。RMoK模型的核心优势在于：

  1. 利用Wav-KAN提取频率和位置信息
  2. 通过JacobiKAN捕捉长期变化趋势
  3. 使用TaylorKAN精确建模局部短期变化

实验结果证实，将这些专家层作为混合专家系统组合使用，能够显著提升模型在预测任务中的表现。需要强调的是，本实验旨在展示如何在Python环境中实现和应用RMoK模型，而非提供一个全面的基准测试。尽管如此，实验结果仍然令人鼓舞，表明RMoK模型在实际应用中具有巨大潜力。

未来研究方向

  1. 在更多样化的数据集上进行全面的基准测试，以进一步验证RMoK模型的泛化能力。
  2. 探索RMoK模型在不同领域（如金融、气象学、生物信息学等）中的应用潜力。
  3. 研究如何进一步优化RMoK模型的架构，以提高其计算效率和预测准确度。
  4. 调研RMoK模型与其他先进技术（如注意力机制、图神经网络等）的结合可能性。

通过持续的研究和改进，相信RMoK模型将在时间序列预测领域发挥越来越重要的作用，为解决复杂的预测问题提供有力支持。

参考资料：

KAN4TSF: Are KAN and KAN-based models Effective for Time Series Forecasting

https://arxiv.org/pdf/2408.11306

KAN: Kolmogorov-Arnold Networks

https://arxiv.org/pdf/2404.19756

RMoK

https://github.com/2448845600/KAN4TSF

标签： 机器学习 时间序列 KAN
登录后发布评论

“KAN专家混合模型在高性能时间序列预测中的应用：RMoK模型架构探析与Python代码实验”的评论:

还没有评论
关于作者
...
Deephub
更多文章请关注公众号：Deephub-IMBA
相关阅读

25 个值得关注的检索增强生成 (RAG) 模型和框架

利用PyTorch的三元组损失Hard Triplet Loss进行嵌入模型微调

告别Print，使用IceCream进行高效的Python调试

为什么卷积现在不火了：CNN研究热度降温的深层原因分析

SMoA: 基于稀疏混合架构的大语言模型协同优化框架

TSMamba：基于Mamba架构的高效时间序列预测基础模型

基于MCMC的贝叶斯营销组合模型评估方法论： 系统化诊断、校准及选择的理论框架

文章导航