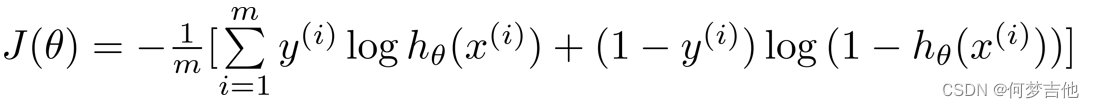【机器学习吴恩达】2022课程笔记（持续更新）

一、机器学习

1.1 机器学习定义

计算机程序从经验E中学习，解决某一任务T，进行某一性能P，通过P测定在T上的表现因经验E而提高

eg：跳棋程序
E：程序自身下的上万盘棋局
T：下跳棋
P：与新对手下跳棋时赢的概率

1.2 监督学习 supervised learning

1.2.1 监督学习定义

给算法一个数据集，其中包含了正确答案，算法的目的是给出更多的正确答案

如预测房价（回归问题）、肿瘤良性恶性分类（分类问题）

1.3 无监督学习 unsupervised learning

1.3.1 无监督学习定义

只给算法一个数据集，但是不给数据集的正确答案，由算法自行分类。

如聚类
1.谷歌新闻每天收集几十万条新闻，并按主题分好类
2.市场通过对用户进行分类，确定目标用户
3.鸡尾酒算法：两个麦克风分别离两个人不同距离，录制两段录音，将两个人的声音分离开来（只需一行代码就可实现，但实现的过程要花大量的时间）

1.3.2 聚类算法

二、单变量的线性回归 univariate linear regression——预测问题

2.1 单变量线性函数

假设函数 hθ(x) = θ0 + θ1x
代价函数****平方误差函数或者平方误差代价函数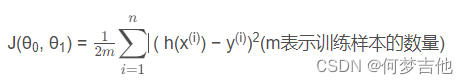
在这里插入图片描述

h(x(i))是预测值，也写做y帽，y(i)是实际值，两者取差
分母的2是为了后续求偏导更好计算。

目标： 最小化代价函数，即minimize J(θ0, θ1)

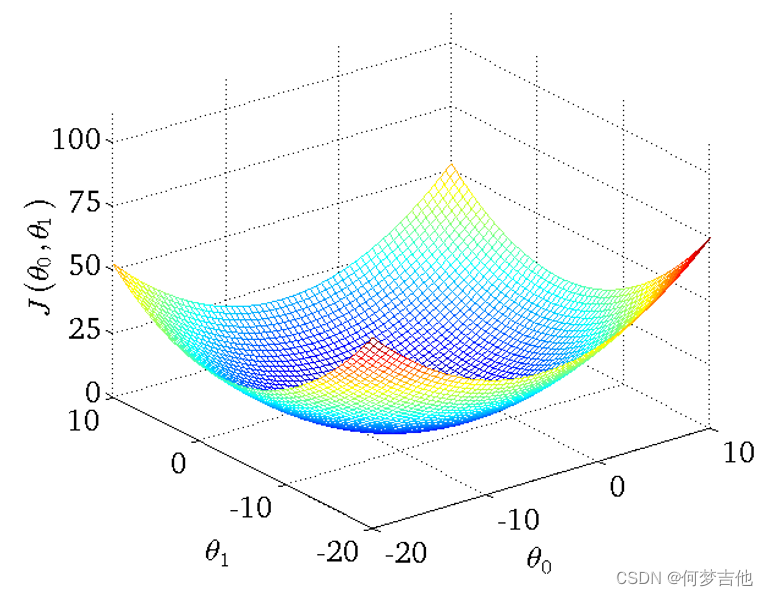
得到的代价函数的三维图如下
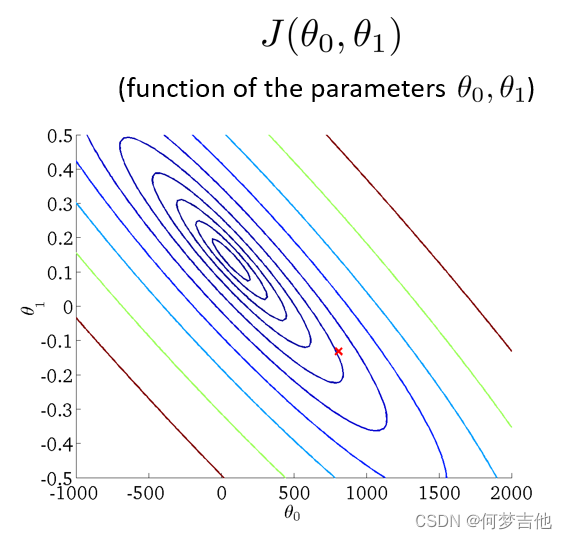
将三维图平面化 等高线图 contour plot 等高线的中心对应最小代价函数

2.2 梯度下降算法 Gradient Descent algorithm

算法思路

指定θ0 和 θ1的初始值
不断改变θ0和θ1的值，使J(θ0,θ1)不断减小
得到一个最小值或局部最小值时停止

梯度：函数中某一点(x, y)的梯度代表函数在该点变化最快的方向
（选用不同的点开始可能达到另一个局部最小值）

梯度下降公式
在这里插入图片描述

θ0和θ1应同步更新，否则如果先更新θ0，会使得θ1是根据更新后的θ0去更新的，与正确结果不相符
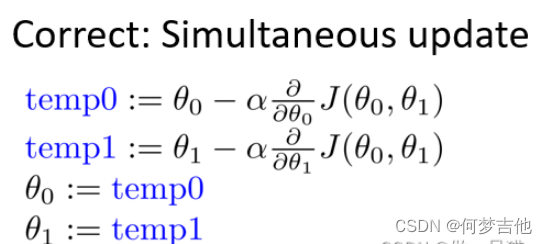
原理：偏导表示的是斜率，斜率在最低点左边为负，最低点右边为正。在移动过程中，偏导值会不断变小，进而移动的步幅也不断变小，最后不断收敛直到到达最低点；在最低点处偏导值为0，不再移动

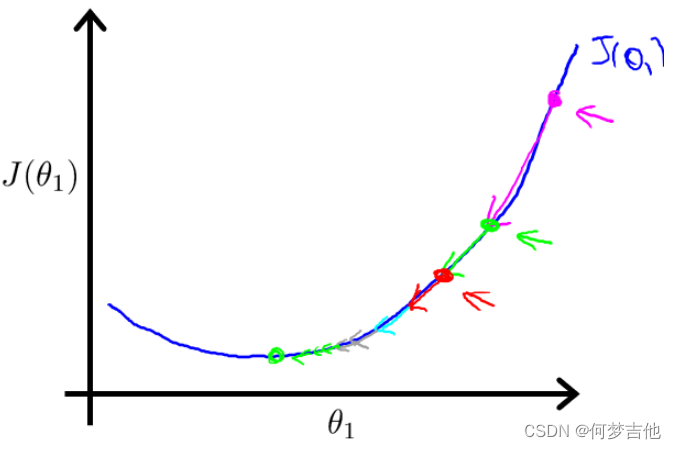
关于α的选择
如果α选择太小，会导致每次移动的步幅都很小，最终需要很多步才能最终收敛
如果α选择太大，会导致每次移动的步幅过大，可能会越过最小值，无法收敛甚至会发散

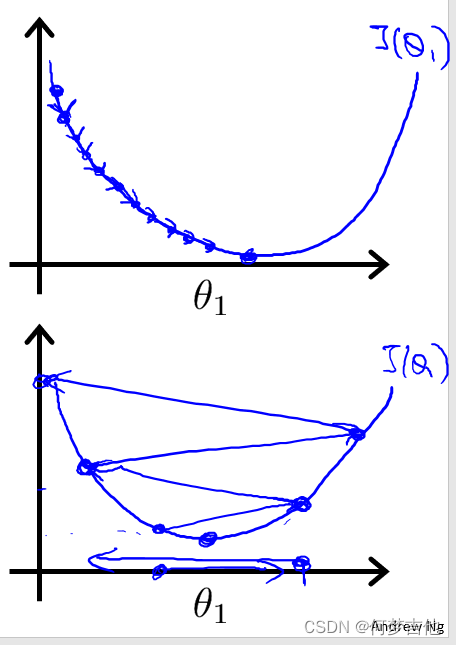
在这里插入图片描述

2.3 用于线性回归的梯度下降 ——Batch梯度下降

公式推导
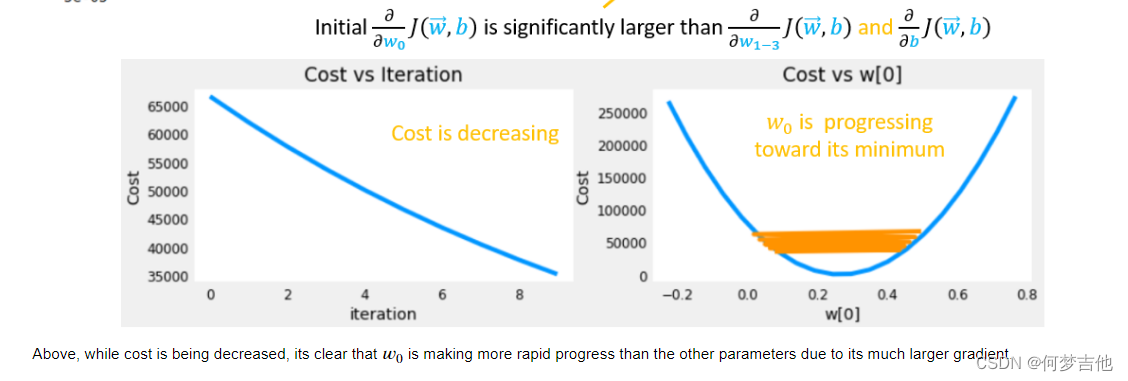
梯度回归的局限性：可能得到的是局部最优解线性回归的梯度下降的函数是凸函数，bowl shape，因此没有局部最优解，只有全局最优解拓展：凸函数与凹函数
批量梯度下降代码实现 批处理是指在一次迭代中运行所有的例子 验证梯度下降是否正常工作的一个好方法是看一下𝐽(𝑤,𝑏)的值。并检查它是否每一步都在减少

defgradient_descent(x, y, w_in, b_in, cost_function, gradient_function, alpha, num_iters):"""
    Performs batch gradient descent to learn theta. Updates theta by taking 
    num_iters gradient steps with learning rate alpha
    
    Args:
      x :    (ndarray): Shape (m,)
      y :    (ndarray): Shape (m,)
      w_in, b_in : (scalar) Initial values of parameters of the model
      cost_function: function to compute cost
      gradient_function: function to compute the gradient
      alpha : (float) Learning rate
      num_iters : (int) number of iterations to run gradient descent
    Returns
      w : (ndarray): Shape (1,) Updated values of parameters of the model after
          running gradient descent
      b : (scalar)                Updated value of parameter of the model after
          running gradient descent
    """# number of training examples
    m =len(x)# An array to store cost J and w's at each iteration — primarily for graphing later
    J_history =[]
    w_history =[]
    w = copy.deepcopy(w_in)#avoid modifying global w within function
    b = b_in
    
    for i inrange(num_iters):# Calculate the gradient and update the parameters
        dj_dw, dj_db = gradient_function(x, y, w, b )# Update Parameters using w, b, alpha and gradient
        w = w - alpha * dj_dw               
        b = b - alpha * dj_db               

        # Save cost J at each iterationif i<100000:# prevent resource exhaustion 
            cost =  cost_function(x, y, w, b)
            J_history.append(cost)# Print cost every at intervals 10 times or as many iterations if < 10if i% math.ceil(num_iters/10)==0:
            w_history.append(w)print(f"Iteration {i:4}: Cost {float(J_history[-1]):8.2f}   ")return w, b, J_history, w_history #return w and J,w history for graphing

三、numpy的向量Vectors、矩阵Matrices

参考课后作业 C1_W2_Lab01_Python_Numpy_Vectorization_Soln
or
网上教程

四、多元线性回归 multiple linear regression

4.1多变量线性回归函数

多元特征表示

在这里插入图片描述

x(i) 表示第 i 组样本
xj(i) 表示第 i 组样本中的第 j 个数据

特征参数
多元变量线性回归模型

4.2 多元梯度下降法 Gradient Descent With Multiple Variables

损失函数计算J
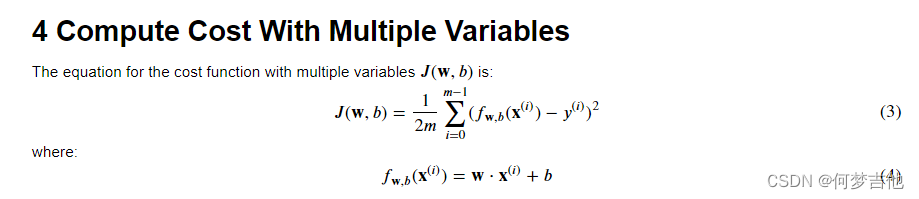
计算梯度
梯度下降实现

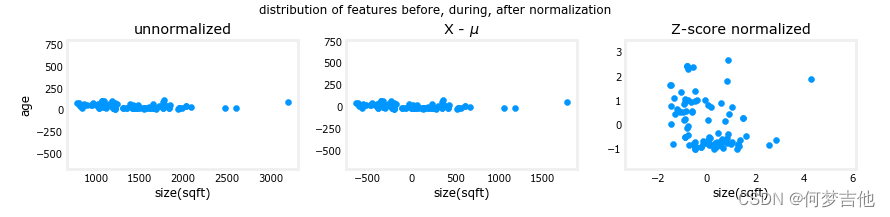
4.3 特征缩放 feature scaling (使具有相似的范围)

目的：让梯度下降运行的更快
问题：当特征范围相差太大时，会一直来回振荡，梯度下降效率低。如下例中，x1范围为0~~2000， x2范围为 1~~5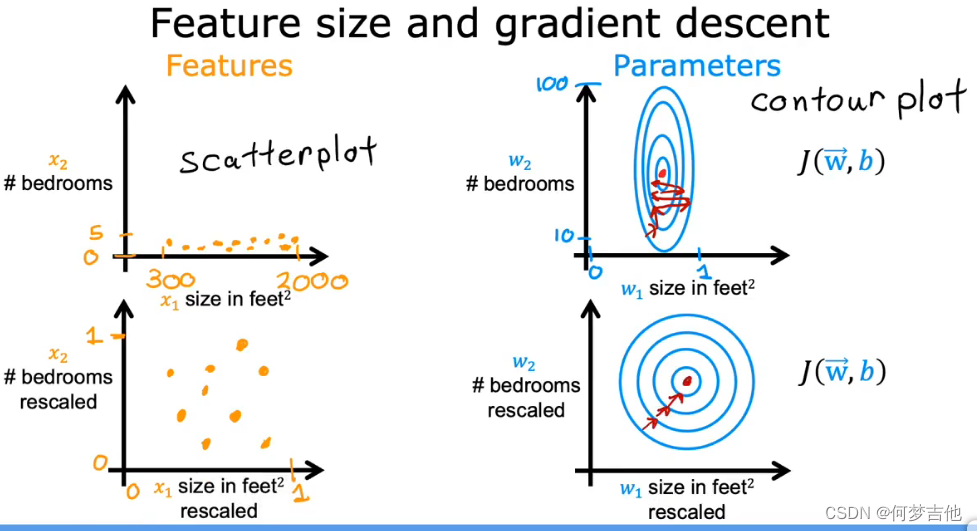

在课后作业 C1_W2_Lab03_Feature_Scaling_and_Learning_Rate_Soln
让中解释了为什么要采用特征缩放=》在梯度下降过程中对参数的更新可以使每个参数的进展相等！！！！！！！

4.3.1 Mean normalization 均值归一化

在这里插入图片描述

4.3.2 Z-score normalization Z-score归一化

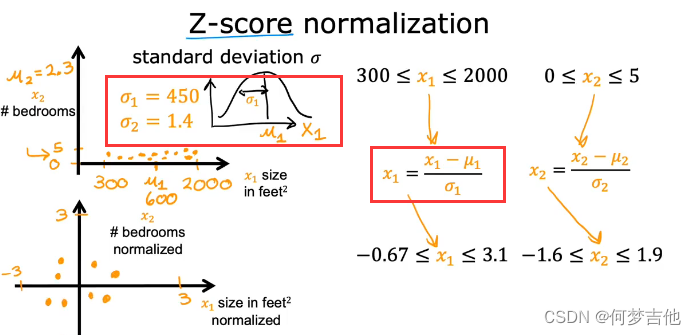
在这里插入图片描述

最终缩放范围

课后作业 C1_W2_Lab03_Feature_Scaling_and_Learning_Rate_Soln
第一步发现从每个特征中去除平均值或平均数值。这就留下了以零为中心的特征。很难看到 "年龄 "特征的差异，但 "尺寸（平方英尺）"显然是在零附近。第二步是除以方差。这使得两个特征都以零为中心，尺度相似。

4.4 如何选择学习率

4.4.1 学习曲线 learning curve

通过学习曲线，可以找到何时可以开始训练我的模型，即多少次iterations后收敛
在这里插入图片描述
还有一种方法是：自动收敛测试 automatic convergence test

4.4.2 学习率的选择

问题：如果学习率太大或者太小的情况、J代码写错了
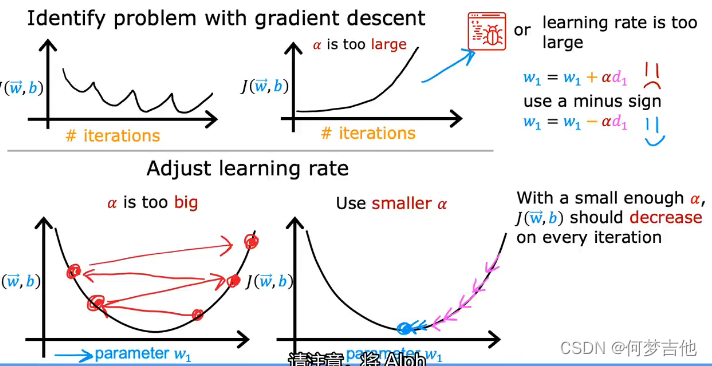
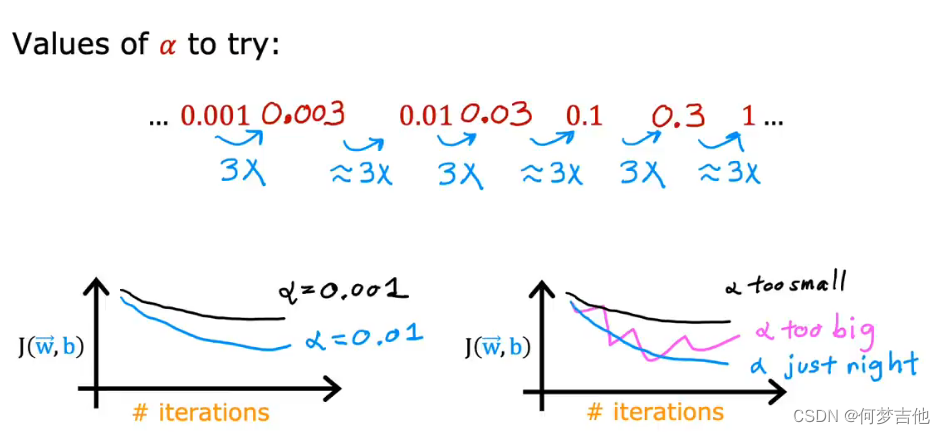
选取合适的α：
…， 0.001，0.003，0.01，0.03，0.1，0.3，1，…以3为倍数找到一个最大值，以该最大值或比该最大值略小的值作为α

4.5 特征和多项式回归polynomial regression

4.5.1 特征工程 feature engineering

通过转换、结合设计新的特征x

假设有两个特征：x1 是土地宽度，x2 是土地纵向深度，则有hθ(x) = θ0 + θ1x1 + θ2x2
由于房价实际与面积挂钩，所以可假设x = x1 * x2，则有hθ(x) = θ0 + θ1x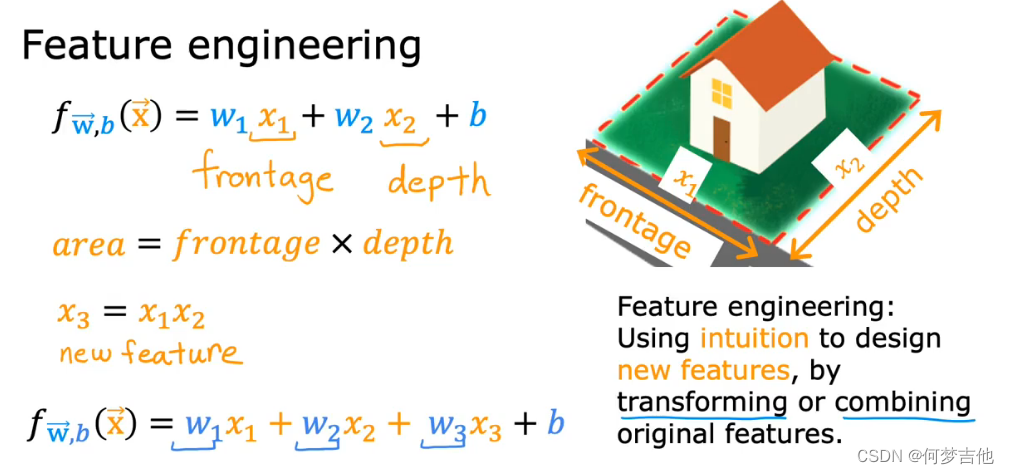
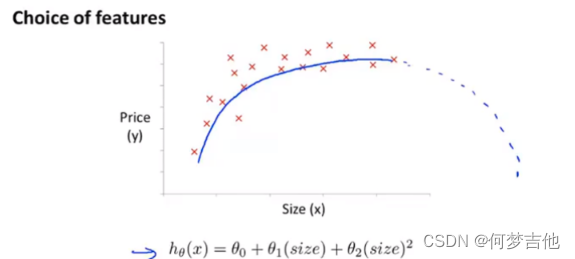
在这里插入图片描述

4.5.2 多项式回归

选用二次模型拟合曲线后半明显下降，不符合实际
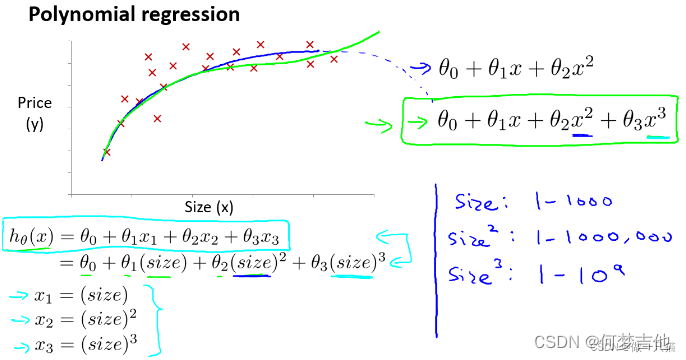
选用三次模型拟合曲线符合实际，但由于次方的出现，要十分注意自变量范围的选取特征被重新标定，特征缩放，让它们彼此之间具有可比性
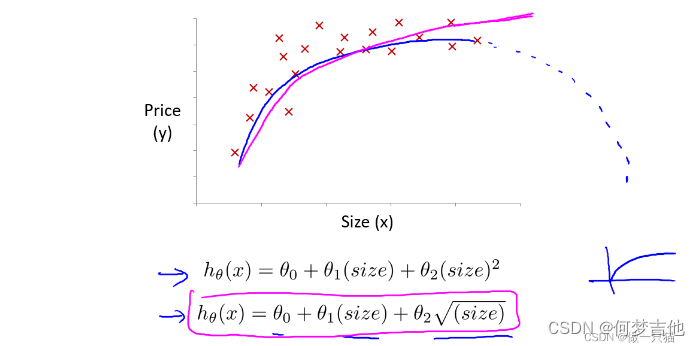
选用根号模型能充分拟合，且自变量范围可变曲度大

五、逻辑回归logistic regression——分类问题

5.1 线性回归对于分类问题的局限性

由于离群点的存在，线性回归不适用于分类问题。
如下图（阈值为0.5），由于最右离群点，再用线性回归与实际情况不拟合。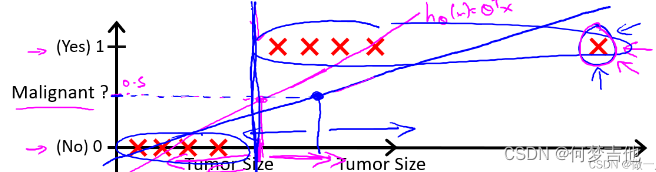
在这里插入图片描述
引入 逻辑回归（logistic regression） 算法，来解决这个问题。

逻辑回归模型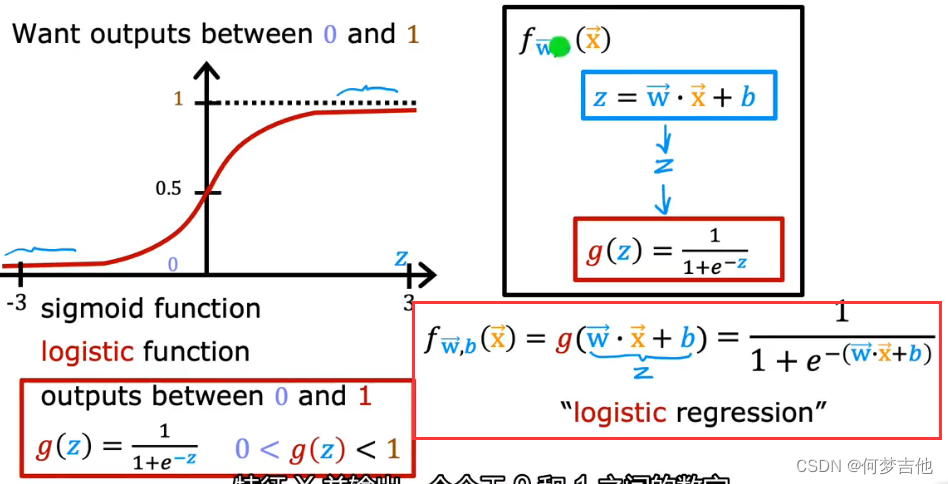sigmoid function === logistic function

课后作业C1_W3_Lab02_Sigmoid_function_Soln
这张图可以更好的帮理解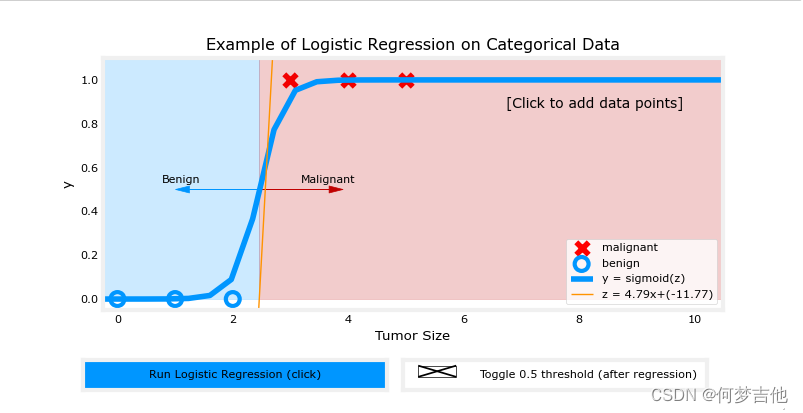
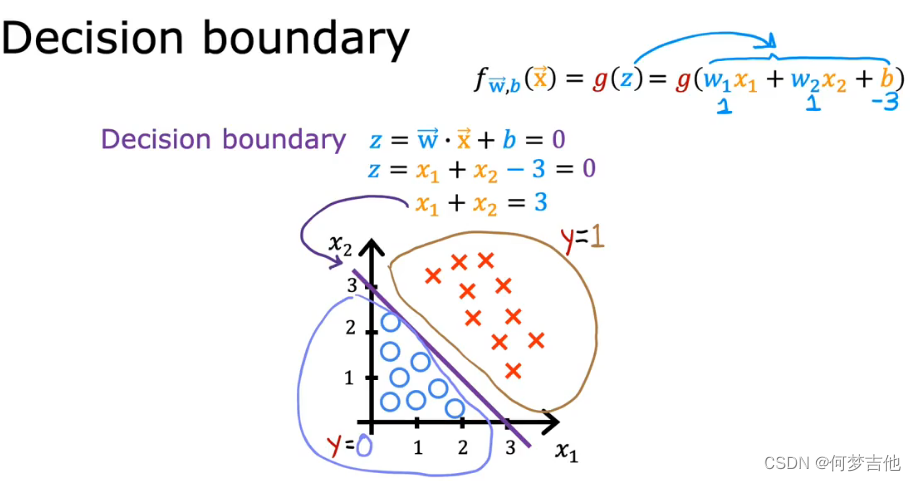
在这里插入图片描述

5.2 决策边界 decision boundary

推导什么情况下是分界线
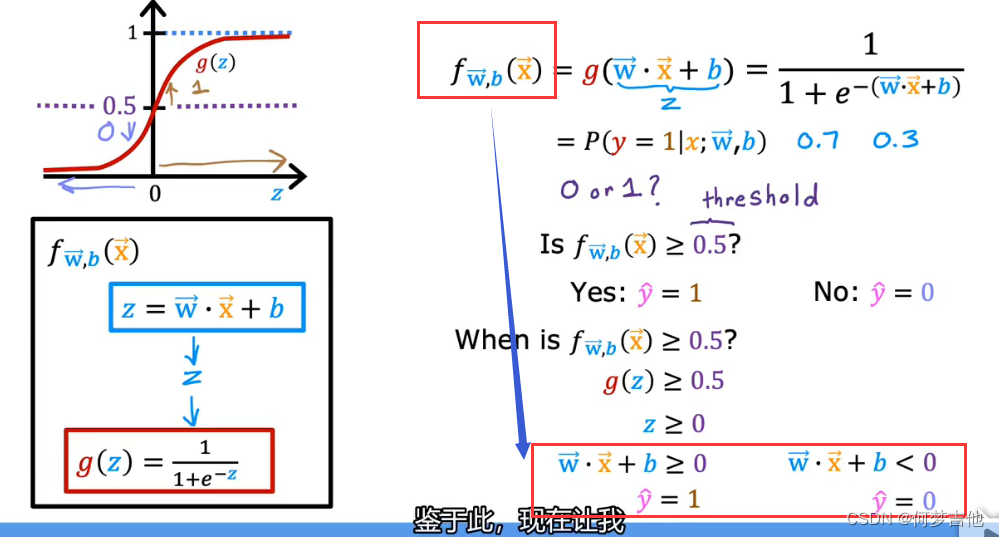
eg1
eg2
eg3

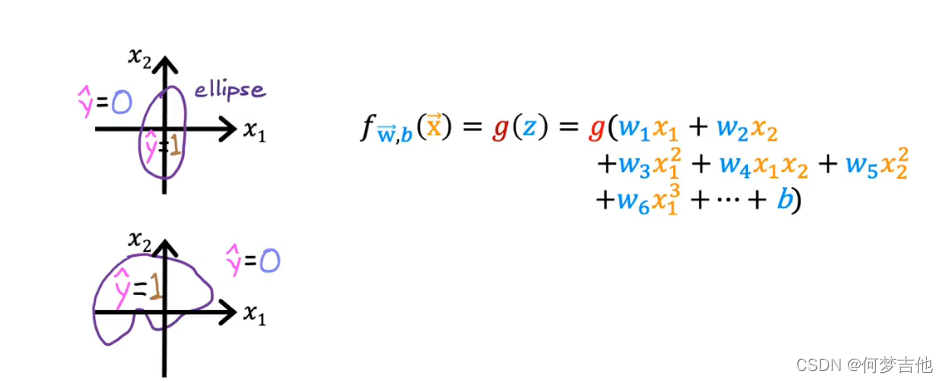
5.3 代价函数 cost function

5.3.1 cost function的导出

问题线性回归的损失函数J 采用的是平方误差squared error cost，应用到分类问题时候的J图像不是convext凸函数，无法用梯度下降找到全局最小值！

将线性回归的代价函数改写为如下形式 （即把1/2提到后面去）
得到逻辑回归的cost function

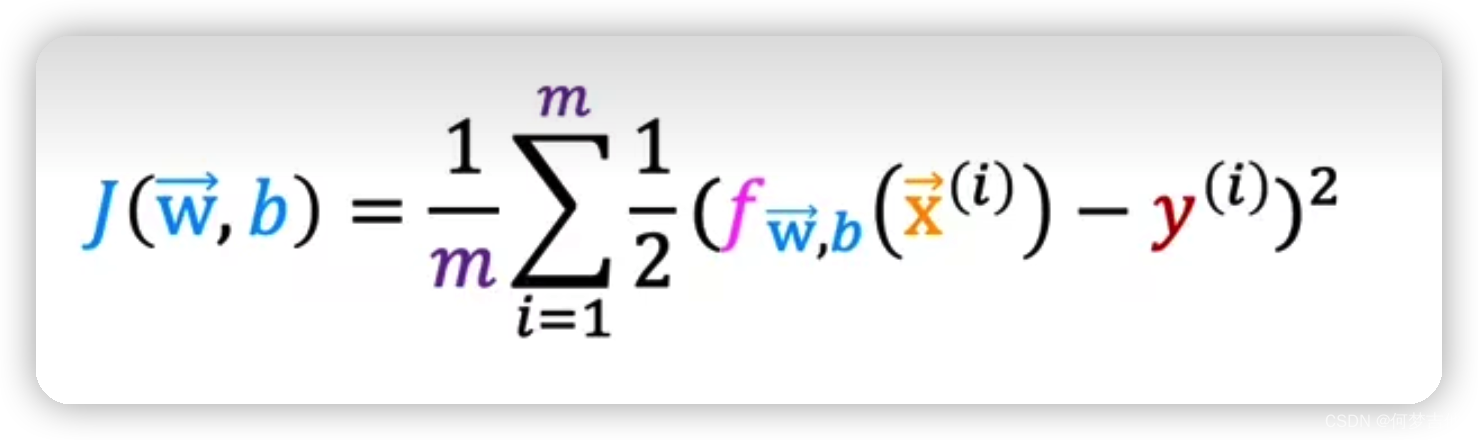
在这里插入图片描述
定义loss function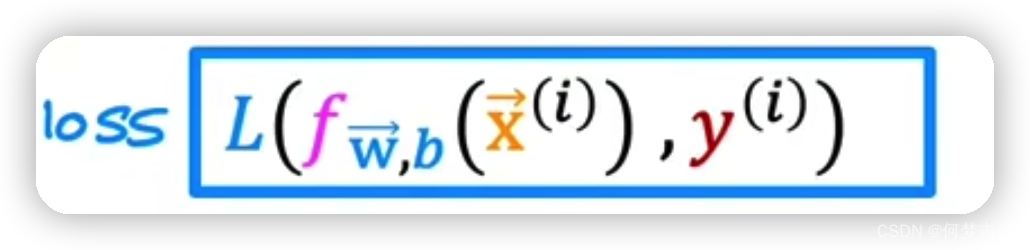

注意区分定义

损失函数 loss function是在一个训练样本的表现，把所有训练样本的损失加起来得到的代价函数cost function，才能衡量模型在整个训练集上的表现

在这里插入图片描述

5.3.2 逻辑回归的损失函数

在这里插入图片描述
y表示实际，hθ(x)表示预测
（hθ(x)就是这里的f wb 因为2021课程用的是hθ(x) 两个课程都有涉及）

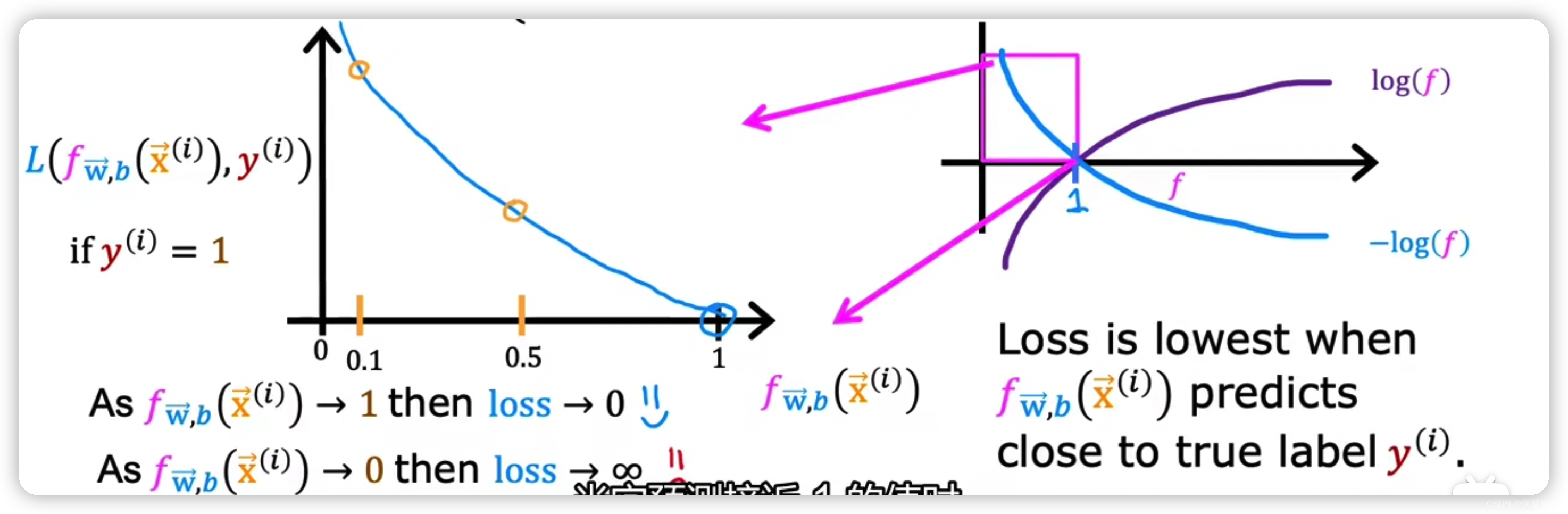
当真是值y = 1时 if 预测hθ(x) = 1, cost = 0 if 预测hθ(x) = 0, cost = ∞ （预测与实际完全不一致，损失函数很大，预测和实际差距很大）

在这里插入图片描述

当真实值y = 0时 if 预测hθ(x) = 0, cost = 0 if 预测hθ(x) = 1, cost = ∞ （预测与实际完全不一致，损失函数很大，预测和实际差距很大）

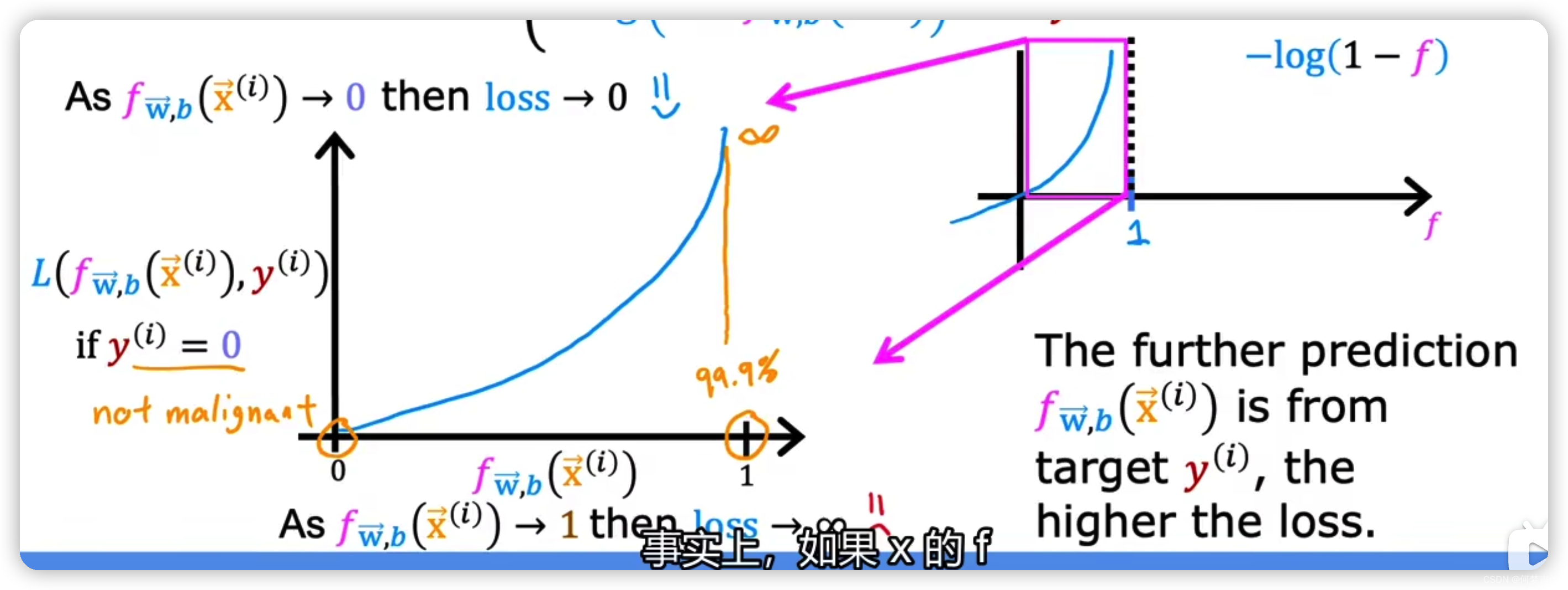
注意一下 f= -log（1-x）图像的画法

5.3.3 简化代价函数与梯度下降

把分类讨论巧妙利用条件合并为一个式子
在这里插入图片描述
进而得到的cost function J 为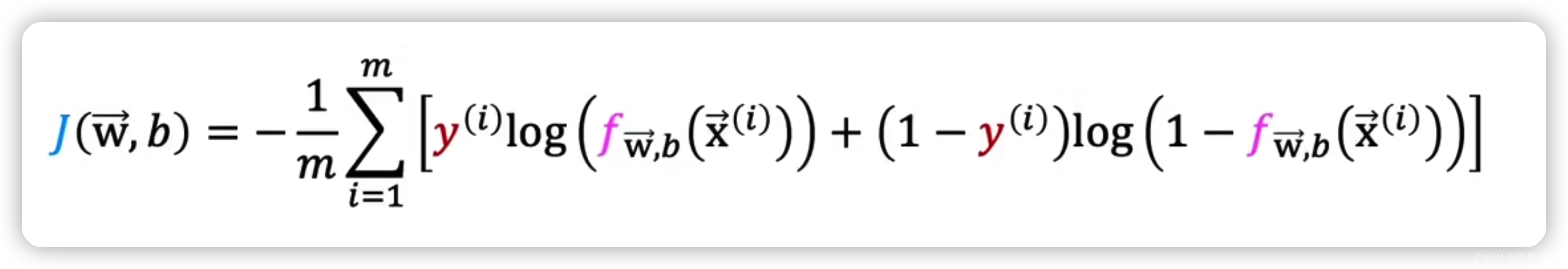

在旧的课程中是这样写的，都是一样的！后面不再赘述！

代价J 是平均损失，是包含m个样本的训练集的平均损失

梯度下降注意： 逻辑回归的梯度下降看似与线性回归的梯度下降相同，但本质不同，因为他们的fx的原型不一样

传送门：逻辑回归梯度下降公式推导

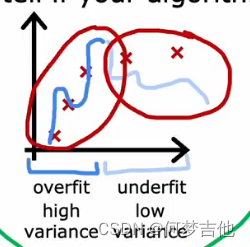
六、过拟合问题

6.1 过拟合定义

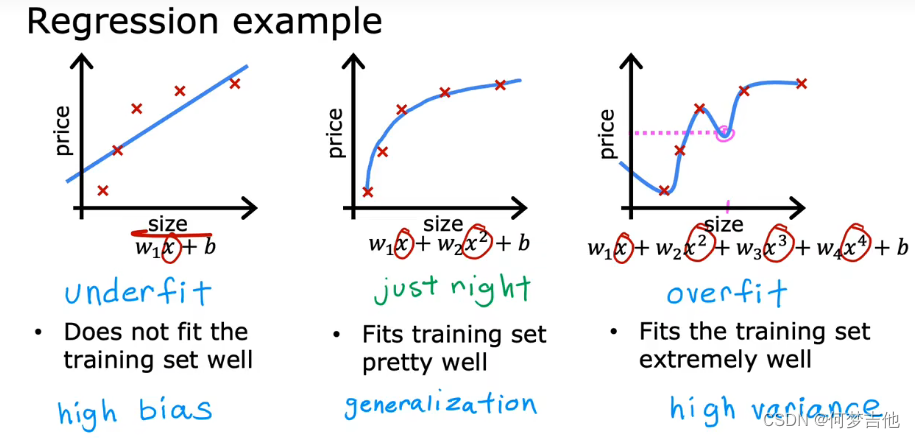
定义****过拟合 当变量过多时，训练出来的假设能很好地拟合训练集，所以代价函数实际上可能非常接近于0，但得到的曲线为了千方百计的拟合数据集，导致它无法泛化到新的样本中，无法预测新样本数据泛化指一个假设模型应用到新样本的能力
例子
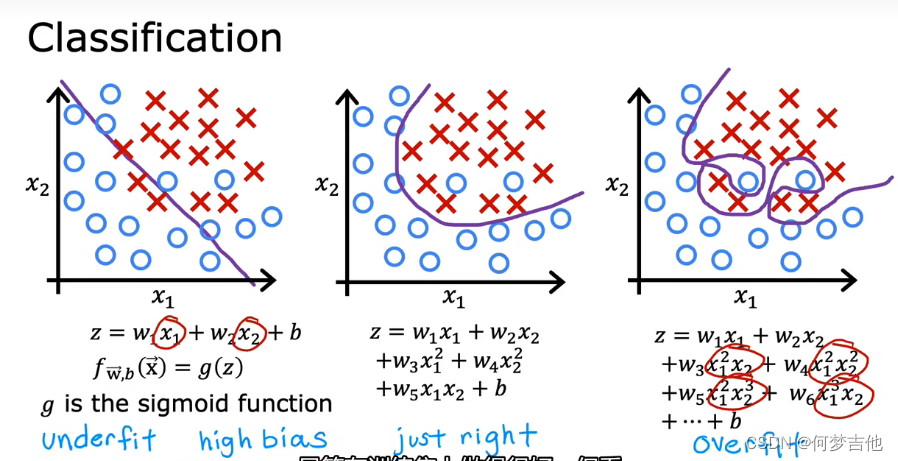
解决过拟合方法1. 得到更多的数据2. 特征选择——选用特征的一部分3. 正则化——减少参数大小

6.2 过拟合的代价函数（正则化原理）

房价预测引入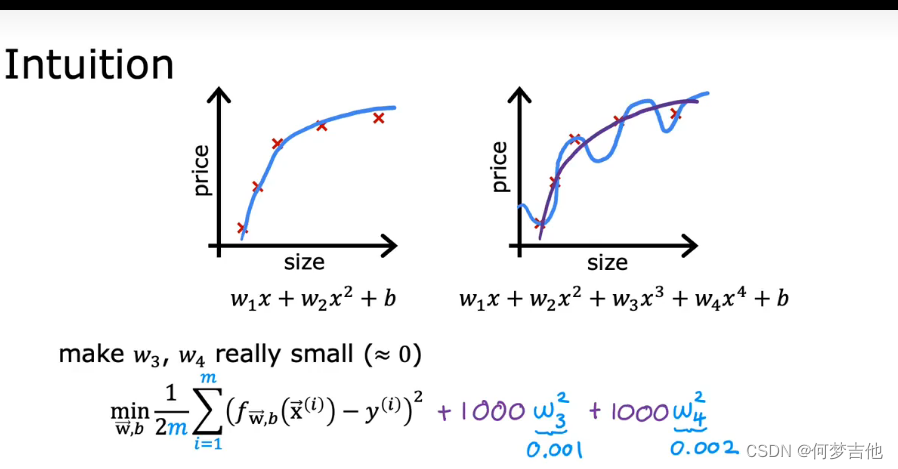以左图为例，其代价函数为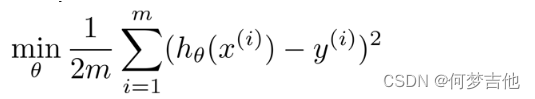在之后再加上两项（1000为任意一个较大的数）

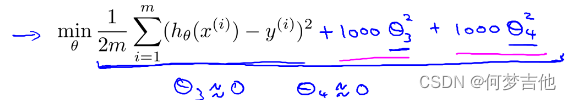
在这里插入图片描述

为了最小化代价函数，自然而然地θ3，θ4要等于0，从而去除了这两项，相当于惩罚这两项使得原来的式子变为二次函数
在一般的回归函数中，使参数的值更小一般会使得曲线更为平滑而减少过拟合情况的发生

引入正则化项的代价函数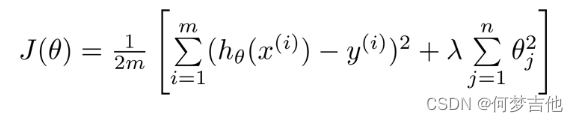1. 如果有很多参数，我们不清楚哪个参数是高阶项，即不知道惩罚哪个能获得更好拟合的结果，因此引入正则化项统一惩罚参数以得到较为简单的函数2. 统一惩罚能得到简单结果是因为，高阶项受到惩罚的效果会更强，反映在图像上就是使其影响变弱3. 其中 .+ 后的一项为正则化项， λ 为正则化参数，作用是控制两个不同目标之间的取舍（1）第一个目标与第一项有关，即我们想要更加拟合数据集 fit data！（2）第二个目标与第二项有关，即我们想要参数θj尽量小 keep θj samll4. 惩罚从θ1到θn，不包括θ0(也就是新版的b)（之所以不惩罚θ0是为了让拟合的函数尽量简单，极端情况就是hθ(x) = θ0，代表的一条水平线，不过实操中有无θ0影响不大）5. 若 λ 设置的过大，即对θ1θ2θ3θ4的惩罚程度过大，导致θ1θ2θ3θ4都接近于0，最后假设模型只剩一个θ0，出现欠拟合情况

原理如下图

在这里插入图片描述

添加正则化项后，代价函数对该权重的偏导变大，即dJ/dw变大。所以w更新时，即w:=w-a(dJ/dw)时，w会变得更小
因为要损失函数尽量小，也就是J尽量小。当lamada很大时，w只能小趋近于0

6.3 用于线性回归的正则方法 Regularized Linear Regression

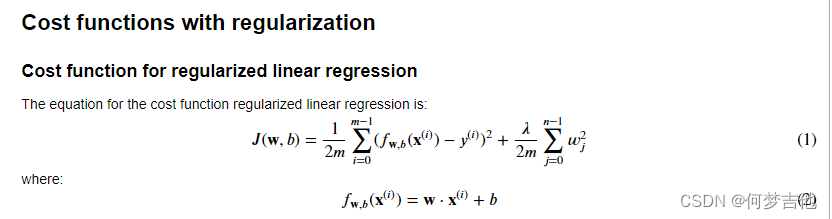
在这里插入图片描述

因为我们没有对b（θ0）正则化，没有试图去缩小b，因此求偏导没有影响

更新公式的数学推导
展开，提项正则化就是在每一次执行gd迭代后，会用一个略微小于1的数乘以wj 执行更新，让wj的值变小了一点，这就解释了为什么正则化可以在每次迭代中shrink 缩小wj的值

代码实现

defcompute_cost_linear_reg(X, y, w, b, lambda_ =1):"""
    Computes the cost over all examples
    Args:
      X (ndarray (m,n): Data, m examples with n features
      y (ndarray (m,)): target values
      w (ndarray (n,)): model parameters  
      b (scalar)      : model parameter
      lambda_ (scalar): Controls amount of regularization
    Returns:
      total_cost (scalar):  cost 
    """

    m  = X.shape[0]
    n  =len(w)
    cost =0.for i inrange(m):
        f_wb_i = np.dot(X[i], w)+ b                                   #(n,)(n,)=scalar, see np.dot
        cost = cost +(f_wb_i - y[i])**2#scalar             
    cost = cost /(2* m)#scalar  
 
    reg_cost =0for j inrange(n):
        reg_cost +=(w[j]**2)#scalar
    reg_cost =(lambda_/(2*m))* reg_cost                              #scalar
    
    total_cost = cost + reg_cost                                       #scalarreturn total_cost                                                  #scalar

6.4 用于线性回归的正则方法 Regularized Linear Regression

当使用很多特征训练逻辑回归时，很容易过拟合，如下图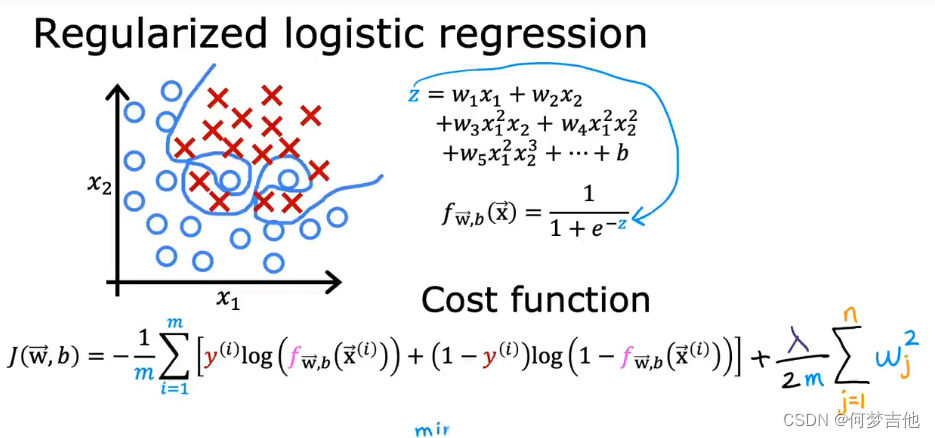在这里插入图片描述
在gd时，更新参数和线性回归类似，只不过这里的f是sigmoid的logistic函数

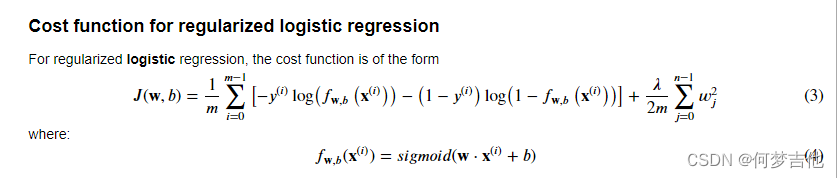
在这里插入图片描述

逻辑回归正则化损失函数代码实现

defcompute_cost_logistic_reg(X, y, w, b, lambda_ =1):"""
    Computes the cost over all examples
    Args:
    Args:
      X (ndarray (m,n): Data, m examples with n features
      y (ndarray (m,)): target values
      w (ndarray (n,)): model parameters  
      b (scalar)      : model parameter
      lambda_ (scalar): Controls amount of regulariza
    Returns:
      total_cost (scalar):  cost 
    """

    m,n  = X.shape
    cost =0.for i inrange(m):
        z_i = np.dot(X[i], w)+ b                                      #(n,)(n,)=scalar, see np.dot
        f_wb_i = sigmoid(z_i)#scalar
        cost +=-y[i]*np.log(f_wb_i)-(1-y[i])*np.log(1-f_wb_i)#scalar
             
    cost = cost/m                                                      #scalar

    reg_cost =0for j inrange(n):
        reg_cost +=(w[j]**2)#scalar
    reg_cost =(lambda_/(2*m))* reg_cost                              #scalar
    
    total_cost = cost + reg_cost                                       #scalarreturn total_cost                                                  #scalar

用正则化计算梯度代码

""" 线性回归 """defcompute_gradient_linear_reg(X, y, w, b, lambda_):"""
    Computes the gradient for linear regression 
    Args:
      X (ndarray (m,n): Data, m examples with n features
      y (ndarray (m,)): target values
      w (ndarray (n,)): model parameters  
      b (scalar)      : model parameter
      lambda_ (scalar): Controls amount of regularization
      
    Returns:
      dj_dw (ndarray (n,)): The gradient of the cost w.r.t. the parameters w. 
      dj_db (scalar):       The gradient of the cost w.r.t. the parameter b. 
    """
    m,n = X.shape           #(number of examples, number of features)
    dj_dw = np.zeros((n,))
    dj_db =0.for i inrange(m):                             
        err =(np.dot(X[i], w)+ b)- y[i]for j inrange(n):                         
            dj_dw[j]= dj_dw[j]+ err * X[i, j]               
        dj_db = dj_db + err                        
    dj_dw = dj_dw / m                                
    dj_db = dj_db / m   
    
    for j inrange(n):
        dj_dw[j]= dj_dw[j]+(lambda_/m)* w[j]return dj_db, dj_dw

 """逻辑回归"""defcompute_gradient_logistic_reg(X, y, w, b, lambda_): 
     。。。。。。。。。。。。。。。。。。。
    for i inrange(m):
        f_wb_i = sigmoid(np.dot(X[i],w)+ b)#(n,)(n,)=scalar
    。。。。。。。。。。。。。。。。。。。

    return dj_db, dj_dw

七、神经网络(深度学习算法)

7.1 认识神经网络

必要性当特征值只有两个时，我们仍可以用之前学过的算法去解决但当特征值很多，且含有很多个多次多项式时，用之前的算法就很难解决了例子：图像感知 Recogonition image 计算机识别汽车是靠像素点的亮度值给定数据集汽车和非汽车的数据，按照之前的方法划分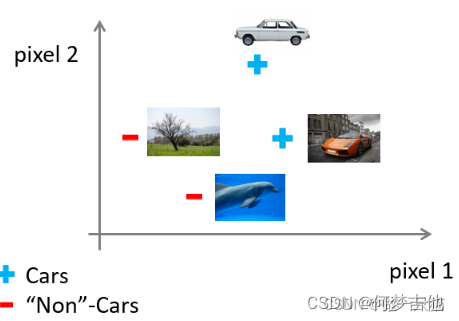可以看到仅针对50*50像素的灰白图片，就有2500个特征值（作为一个特征向量input ）。当引入rgb时，特征值达到了7500个，如果算上多次多项式，特征值达到了三百万个，显然再继续用之前的算法难以处理这么庞大的数据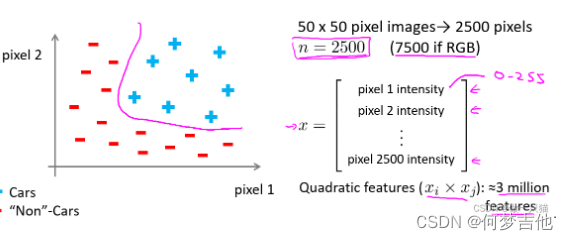而神经网络做法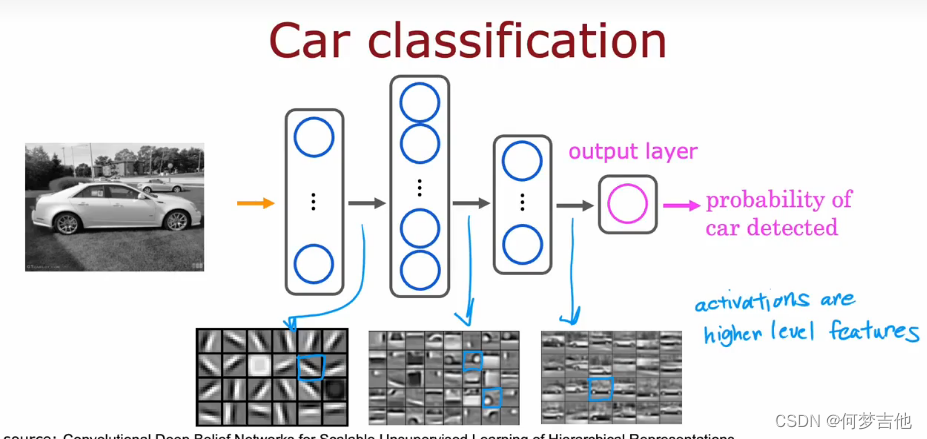

7.2 如何在神经网络上推理

7.2.1 神经网络的定义

定义一个神经网络如下：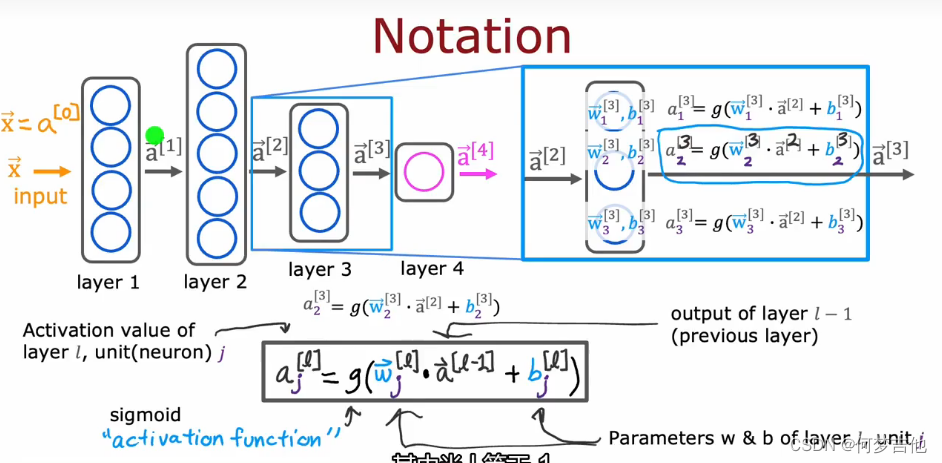
在这里插入图片描述

计算第l层第j个激活值的公式
在这里插入图片描述

注意符号的含义 w2_1 上标2代表layer 2 下标 1代表第一个神经元

7.2.2 构建：前向传播 forward propagation （使用TensorFlow实现）

https://blog.csdn.net/weixin_42301220/article/details/123915977

例子：手写识别01 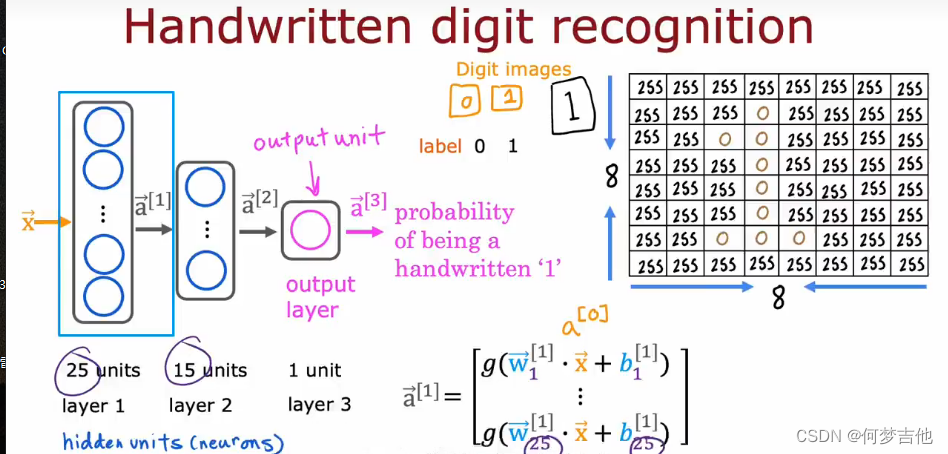每次层计算，从左往右计算，要传播神经元的激活值
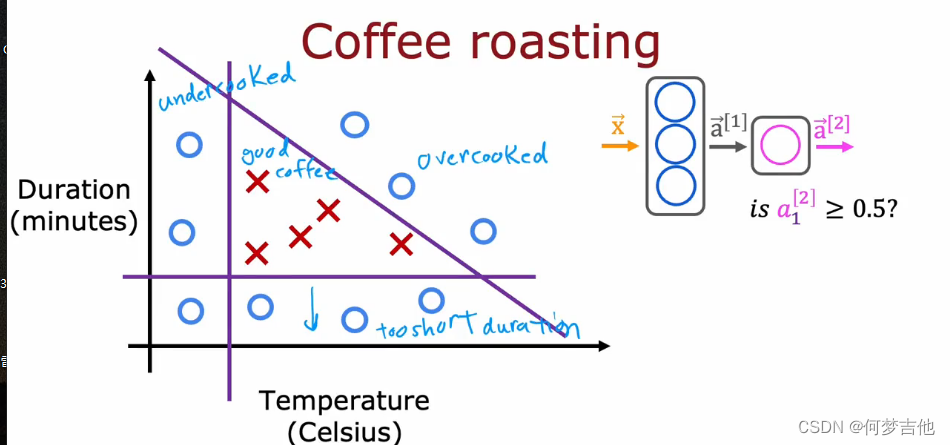
例子：烤咖啡的好坏
python实现前向传播理解

自定义dense密集函数：输入前一层的激活，给定当前层的参数，它会输出下一层激活值自定义sequential函数
其中：W大写在线性代数中代表矩阵

TensorFlow 实现前向传播
拓展： AGI 通用人工智能

7.2.3 矢量化（让神经网络运行更快）

上面python代码实现前向传播可以用更简洁的向量化

7.2.4 矩阵乘法

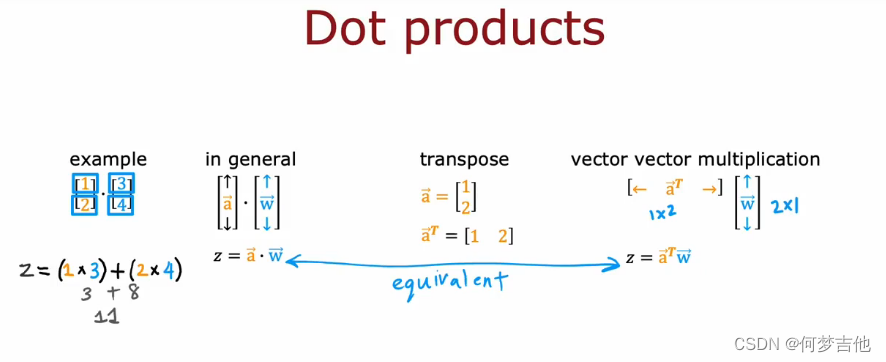
向量点积dot products
矩阵乘法矩阵就看做一个个列向量组成的

这也解释了为什么矩阵乘法形状要邻接相同 12 23 ，因为长度相同的向量才能dot product！！！

在这里插入图片描述

代码理解，为什么TensorFlow可以

在这里插入图片描述
TensorFlow 默认样本是行向量，而非列向量，因此不需要转置直接写作A，而非AT

输入的一个行向量包含所有特征，其中每一列是一个特征

7.2.5 C2_W1_Assignment 01识别

每一层参数矩阵形状的分析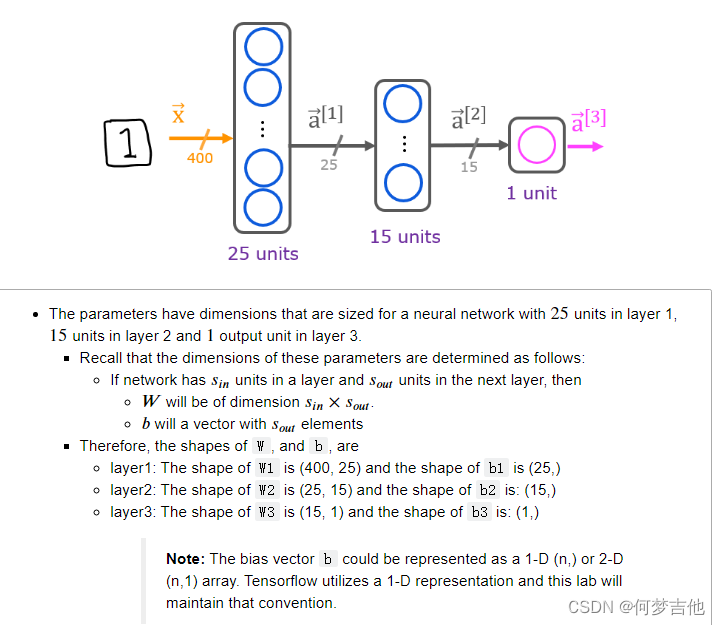
在这里插入图片描述
Tensorflow模型是逐层建立的。你指定一个层的输出尺寸，这决定了下一层的输入尺寸。
注意：也可以添加一个输入层，指定第一层的输入维度。例如。 tf.keras.Input(shape=(400,)), #指定输入形状

构建神经网络

# UNQ_C1# GRADED CELL: Sequential model

model = Sequential([               
        tf.keras.Input(shape=(400,)),#specify input size### START CODE HERE ### 
        Dense(25, activation='sigmoid'), 
        Dense(15, activation='sigmoid'), 
        Dense(1,  activation='sigmoid')### END CODE HERE ### ], name ="my_model")

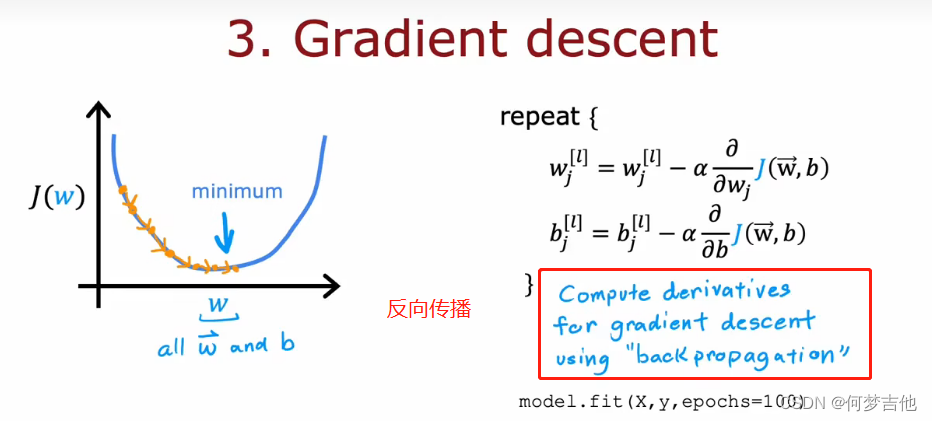
7.4 训练神经网络

7.4.1 模型训练细节

eg 对于01手写分类问题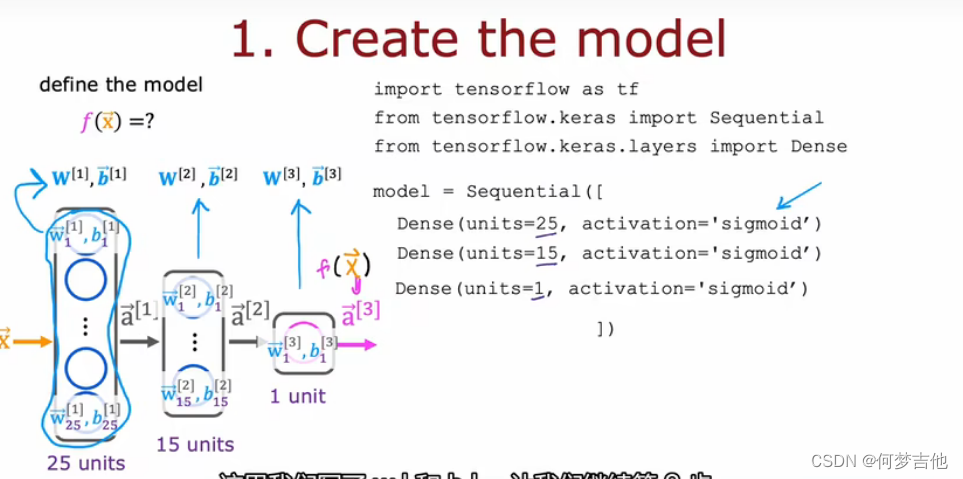
在这里插入图片描述
对于逻辑回归二分类问题用Binary Cross Entropy二元交叉熵损失函数

使用二元交叉熵作为损失函数时，我们通常使用以下公式来计算单个样本的损失：

      l 
     
    
      o 
     
    
      s 
     
    
      s 
     
    
      = 
     
    
      − 
     
    
      [ 
     
    
      y 
     
    
      l 
     
    
      o 
     
    
      g 
     
    
      ( 
     
    
      p 
     
    
      ) 
     
    
      + 
     
    
      ( 
     
    
      1 
     
    
      − 
     
    
      y 
     
    
      ) 
     
    
      l 
     
    
      o 
     
    
      g 
     
    
      ( 
     
    
      1 
     
    
      − 
     
    
      p 
     
    
      ) 
     
    
      ] 
     
    
   
     loss = -[ylog(p) + (1-y)log(1-p)] 
    
   
 loss=−[ylog(p)+(1−y)log(1−p)]

其中，

      y 
     
    
   
     y 
    
   
 y是真实标签（0或1）， 
  
   
    
    
      p 
     
    
   
     p 
    
   
 p是预测值（0到1之间的概率值）。这个公式表示，当真实标签为1时，我们希望预测值 
  
   
    
    
      p 
     
    
   
     p 
    
   
 p越接近1，此时损失越小，等于 
  
   
    
    
      − 
     
    
      l 
     
    
      o 
     
    
      g 
     
    
      ( 
     
    
      p 
     
    
      ) 
     
    
   
     -log(p) 
    
   
 −log(p)；

当真实标签为0时，我们希望预测值

      p 
     
    
   
     p 
    
   
 p越接近0，此时损失也越小，等于 
  
   
    
    
      − 
     
    
      l 
     
    
      o 
     
    
      g 
     
    
      ( 
     
    
      1 
     
    
      − 
     
    
      p 
     
    
      ) 
     
    
   
     -log(1-p) 
    
   
 −log(1−p)。

https://blog.csdn.net/Cy_coding/article/details/116427968

在这里插入图片描述

7.4.2 如何选择激活函数

ReLU激活函数
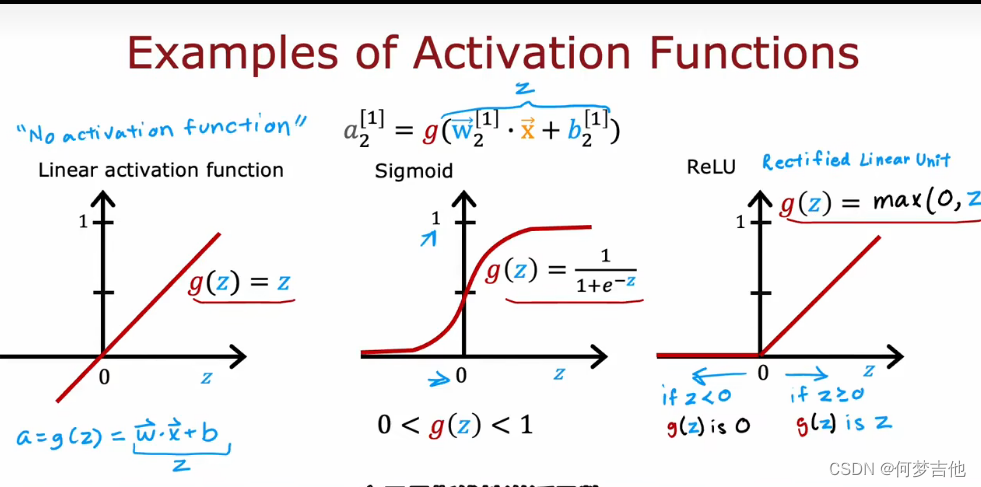
对于输出层激活函数的选择根据输出的y的取值范围
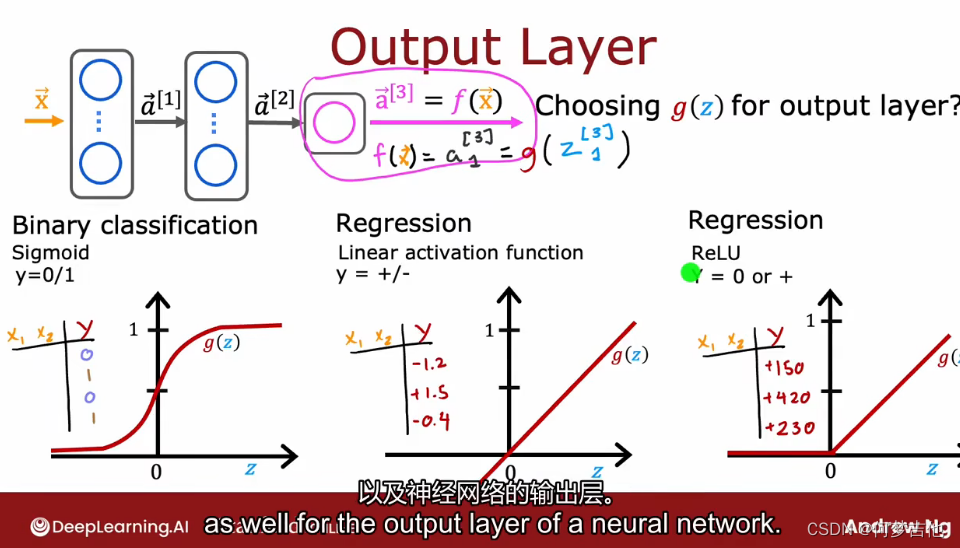
hidden layer 隐藏层除非是二分类问题用sigmoid，一般默认用relu，不能用线性激活函数，否则不能拟合，就相当于一个线性回归了因为 1. relu计算很快，2. 并且只有右边扁平flat，而sigmoid有两处flat，会影响gd的速度（因为激活函数是计算偏导的一部分）

当激活函数平的地方越多，在梯度下降的时候速度越慢，因为求导是求斜率，平的斜率就很小很小，因此sigmoid速度慢于RULu

7.5 多分类问题

7.5.1 softmax 回归算法

以下来自ChatGPT

Softmax 回归算法的基本思想是将输入数据映射到多个类别之一，并为每个类别分配一个概率。算法的输入是一个 **

      n 
     
    
   
     n 
    
   
 n 维特征向量  
  
   
    
    
      x 
     
    
   
     x 
    
   
 x**，输出是  
 
  
   
   
     K 
    
   
  
    K 
   
  
K 个类别的概率分布，其中 ** 
  
   
    
    
      K 
     
    
   
     K 
    
   
 K 是类别的数量**。

Softmax 回归算法的模型可以表示为：

      P 
     
    
      ( 
     
    
      y 
     
    
      = 
     
    
      k 
     
    
      ∣ 
     
    
      x 
     
    
      , 
     
    
      W 
     
    
      ) 
     
    
      = 
     
     
      
      
        exp 
       
      
        ⁡ 
       
      
        ( 
       
       
       
         w 
        
       
         k 
        
       
         T 
        
       
      
        x 
       
      
        ) 
       
      
      
       
       
         ∑ 
        
        
        
          j 
         
        
          = 
         
        
          1 
         
        
       
         K 
        
       
      
        exp 
       
      
        ⁡ 
       
      
        ( 
       
       
       
         w 
        
       
         j 
        
       
         T 
        
       
      
        x 
       
      
        ) 
       
      
     
    
   
     P(y=k|x,W) = \frac{\exp(w_k^Tx)}{\sum_{j=1}^K \exp(w_j^Tx)} 
    
   
 P(y=k∣x,W)=∑j=1Kexp(wjTx)exp(wkTx)

其中，

     P 
    
   
     ( 
    
   
     y 
    
   
     = 
    
   
     k 
    
   
     ∣ 
    
   
     x 
    
   
     , 
    
   
     W 
    
   
     ) 
    
   
  
    P(y=k|x,W) 
   
  
P(y=k∣x,W) 表示给定输入  
 
  
   
   
     x 
    
   
  
    x 
   
  
x 时，模型预测  
 
  
   
   
     y 
    
   
     = 
    
   
     k 
    
   
  
    y=k 
   
  
y=k 的概率；** 
  
   
    
     
     
       w 
      
     
       k 
      
     
    
   
     w_k 
    
   
 wk 是一个  
  
   
    
    
      n 
     
    
   
     n 
    
   
 n 维向量，表示第  
  
   
    
    
      k 
     
    
   
     k 
    
   
 k 个类别的参数**； 
 
  
   
   
     W 
    
   
  
    W 
   
  
W 是一个  
 
  
   
   
     n 
    
   
     × 
    
   
     K 
    
   
  
    n\times K 
   
  
n×K 的**参数矩阵，其中每一列对应一个类别的参数。**

损失函数（Loss Function）

对于一个**单独的样本

      ( 
     
    
      x 
     
    
      , 
     
    
      y 
     
    
      ) 
     
    
   
     (x, y) 
    
   
 (x,y)**，其中 ** 
  
   
    
    
      x 
     
    
   
     x 
    
   
 x 是输入特征， 
  
   
    
    
      y 
     
    
   
     y 
    
   
 y 是输出类别**，假设 Softmax 回归模型的输出为  
 
  
   
   
     P 
    
   
     ( 
    
   
     y 
    
   
     = 
    
   
     k 
    
   
     ∣ 
    
   
     x 
    
   
     , 
    
   
     W 
    
   
     ) 
    
   
  
    P(y=k|x,W) 
   
  
P(y=k∣x,W)，即输入  
 
  
   
   
     x 
    
   
  
    x 
   
  
x 在给定参数  
 
  
   
   
     W 
    
   
  
    W 
   
  
W 下属于类别  
 
  
   
   
     k 
    
   
  
    k 
   
  
k 的概率，则该样本的交叉熵损失函数可以表示为：


  
   
    
    
      L 
     
    
      ( 
     
    
      W 
     
    
      ; 
     
    
      x 
     
    
      , 
     
    
      y 
     
    
      ) 
     
    
      = 
     
    
      − 
     
     
     
       ∑ 
      
      
      
        k 
       
      
        = 
       
      
        1 
       
      
     
       K 
      
     
     
     
       y 
      
     
       k 
      
     
    
      log 
     
    
      ⁡ 
     
    
      P 
     
    
      ( 
     
    
      y 
     
    
      = 
     
    
      k 
     
    
      ∣ 
     
    
      x 
     
    
      , 
     
    
      W 
     
    
      ) 
     
    
   
     L(W; x, y) = - \sum_{k=1}^K y_k \log P(y=k|x,W) 
    
   
 L(W;x,y)=−k=1∑KyklogP(y=k∣x,W)

其中，**

       y 
      
     
       k 
      
     
    
   
     y_k 
    
   
 yk 表示真实标签的 one-hot 编码形式**， 
 
  
   
   
     K 
    
   
  
    K 
   
  
K 是类别总数。

损失函数的意义是表示模型对于该样本的预测值与真实值之间的差距，当模型对于每个样本的预测概率越接近真实标签时，损失函数越小，模型的分类准确度越高。（可以画图分析）

在 Softmax 回归算法中，通常使用交叉熵（Cross-entropy）作为代价函数（Cost Function）。

对于一个训练集

     D 
    
   
     = 
    
    
     
     
       ( 
      
      
      
        x 
       
      
        i 
       
      
     
       , 
      
      
      
        y 
       
      
        i 
       
      
     
       ) 
      
     
     
     
       i 
      
     
       = 
      
     
       1 
      
     
    
      m 
     
    
   
  
    D={(x_i,y_i)}_{i=1}^m 
   
  
D=(xi,yi)i=1m ，其中 ** 
  
   
    
     
     
       x 
      
     
       i 
      
     
    
   
     x_i 
    
   
 xi 是第  
  
   
    
    
      i 
     
    
   
     i 
    
   
 i 个样本的特征向量， 
  
   
    
     
     
       y 
      
     
       i 
      
     
    
   
     y_i 
    
   
 yi 是第  
  
   
    
    
      i 
     
    
   
     i 
    
   
 i 个样本的类别**，其取值为  
 
  
   
   
     1 
    
   
     , 
    
   
     2 
    
   
     , 
    
   
     … 
    
   
     , 
    
   
     K 
    
   
  
    1, 2, \ldots, K 
   
  
1,2,…,K 中的一个。模型的参数为  
 
  
   
   
     W 
    
   
  
    W 
   
  
W。则 **Softmax 回归模型的交叉熵代价函数**可以表示为：


  
   
    
    
      J 
     
    
      ( 
     
    
      W 
     
    
      ) 
     
    
      = 
     
    
      − 
     
     
     
       1 
      
     
       m 
      
     
     
     
       ∑ 
      
      
      
        i 
       
      
        = 
       
      
        1 
       
      
     
       m 
      
     
     
     
       ∑ 
      
      
      
        k 
       
      
        = 
       
      
        1 
       
      
     
       K 
      
     
     
     
       y 
      
      
      
        i 
       
      
        , 
       
      
        k 
       
      
     
    
      log 
     
    
      ⁡ 
     
     
      
      
        exp 
       
      
        ⁡ 
       
      
        ( 
       
       
       
         w 
        
       
         k 
        
       
         T 
        
       
       
       
         x 
        
       
         i 
        
       
      
        ) 
       
      
      
       
       
         ∑ 
        
        
        
          j 
         
        
          = 
         
        
          1 
         
        
       
         K 
        
       
      
        exp 
       
      
        ⁡ 
       
      
        ( 
       
       
       
         w 
        
       
         j 
        
       
         T 
        
       
       
       
         x 
        
       
         i 
        
       
      
        ) 
       
      
     
    
   
     J(W)=-\frac{1}{m}\sum_{i=1}^m \sum_{k=1}^K y_{i,k}\log\frac{\exp(w_k^Tx_i)}{\sum_{j=1}^K \exp(w_j^Tx_i)} 
    
   
 J(W)=−m1i=1∑mk=1∑Kyi,klog∑j=1Kexp(wjTxi)exp(wkTxi)

其中 **

       y 
      
      
      
        i 
       
      
        , 
       
      
        k 
       
      
     
    
   
     y_{i,k} 
    
   
 yi,k 是一个 K 维向量，表示第  
  
   
    
    
      i 
     
    
   
     i 
    
   
 i 个样本的实际输出**，对应于第  
 
  
   
   
     k 
    
   
  
    k 
   
  
k 个类别，只有一个元素为  
 
  
   
   
     1 
    
   
  
    1 
   
  
1，其余为  
 
  
   
   
     0 
    
   
  
    0 
   
  
0。

这个代价函数的含义是对于所有的样本，求预测值与真实值之间的差距，并对这个差距取平均。

训练 Softmax 回归模型通常使用最大似然估计方法。给定一个训练集

     D 
    
   
     = 
    
    
     
     
       ( 
      
      
      
        x 
       
      
        i 
       
      
     
       , 
      
      
      
        y 
       
      
        i 
       
      
     
       ) 
      
     
     
     
       i 
      
     
       = 
      
     
       1 
      
     
    
      m 
     
    
   
  
    D={(x_i,y_i)}_{i=1}^m 
   
  
D=(xi,yi)i=1m，其中  
 
  
   
    
    
      x 
     
    
      i 
     
    
   
  
    x_i 
   
  
xi 是第  
 
  
   
   
     i 
    
   
  
    i 
   
  
i 个样本的特征向量， 
 
  
   
    
    
      y 
     
    
      i 
     
    
   
  
    y_i 
   
  
yi 是第  
 
  
   
   
     i 
    
   
  
    i 
   
  
i 个样本的类别，**模型的参数可以通过最大化训练集的似然函数得到：**


  
   
    
    
      arg 
     
    
      ⁡ 
     
     
      
      
        max 
       
      
        ⁡ 
       
      
     
       W 
      
     
     
     
       ∏ 
      
      
      
        i 
       
      
        = 
       
      
        1 
       
      
     
       m 
      
     
    
      P 
     
    
      ( 
     
     
     
       y 
      
     
       i 
      
     
    
      ∣ 
     
     
     
       x 
      
     
       i 
      
     
    
      , 
     
    
      W 
     
    
      ) 
     
    
   
     \arg\max_W \prod_{i=1}^m P(y_i|x_i,W) 
    
   
 argWmaxi=1∏mP(yi∣xi,W)

这个最大化问题通常可以通过梯度下降等优化方法求解。

在 Softmax 回归算法中，我们需要通过训练数据来获得模型的参数，通常使用随机梯度下降（Stochastic Gradient Descent，SGD）等优化算法来最小化损失函数，从而获得模型的参数。

具体来说，我们需要先将训练集分成小批量数据，每个小批量数据包含

     n 
    
   
  
    n 
   
  
n 个样本。对于每个小批量数据，计算其平均损失，并计算损失函数对于模型参数的梯度。然后，根据计算出的梯度更新模型的参数，重复这个过程直到满足停止条件（例如达到指定的迭代次数或者损失函数已经收敛）。

对于 Softmax 回归算法，由于采用了交叉熵损失函数，所以可以直接通过梯度下降来最小化损失函数（凸函数，因此不存在局部最小值。这意味着梯度下降等优化算法可以在有限次迭代后找到全局最小值），从而获得模型的参数。具体来说，模型参数的更新公式可以表示为：

      W 
     
    
      ← 
     
    
      W 
     
    
      − 
     
    
      η 
     
     
      
      
        ∂ 
       
      
        L 
       
      
        ( 
       
      
        W 
       
      
        ; 
       
       
       
         x 
        
       
         i 
        
       
      
        , 
       
       
       
         y 
        
       
         i 
        
       
      
        ) 
       
      
      
      
        ∂ 
       
      
        W 
       
      
     
    
   
     W \leftarrow W - \eta \frac{\partial L(W;x_i, y_i)}{\partial W} 
    
   
 W←W−η∂W∂L(W;xi,yi)

其中

     W 
    
   
  
    W 
   
  
W 表示模型参数， 
 
  
   
   
     η 
    
   
  
    \eta 
   
  
η 是学习率， 
 
  
   
    
     
     
       ∂ 
      
     
       L 
      
     
       ( 
      
     
       W 
      
     
       ; 
      
      
      
        x 
       
      
        i 
       
      
     
       , 
      
      
      
        y 
       
      
        i 
       
      
     
       ) 
      
     
     
     
       ∂ 
      
     
       W 
      
     
    
   
  
    \frac{\partial L(W;x_i, y_i)}{\partial W} 
   
  
∂W∂L(W;xi,yi) 表示损失函数对于模型参数的梯度。

在实际应用中，通常需要对数据进行预处理，例如归一化、标准化等，以及添加正则化项来防止过拟合。此外，还可以使用其他优化算法如 Adam、Adagrad 等来替代随机梯度下降算法。

Softmax 回归算法的模型

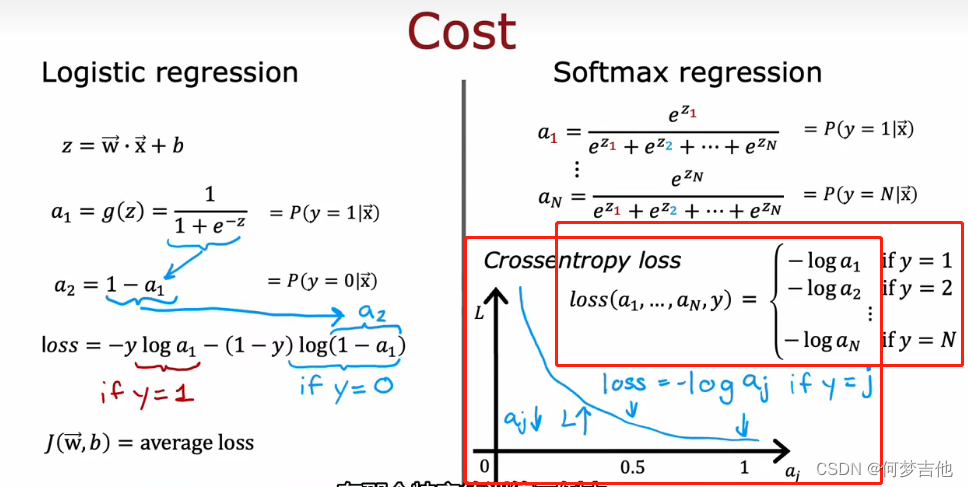
在这里插入图片描述

成本函数代价函数cost function loss function定义
输出层计算方式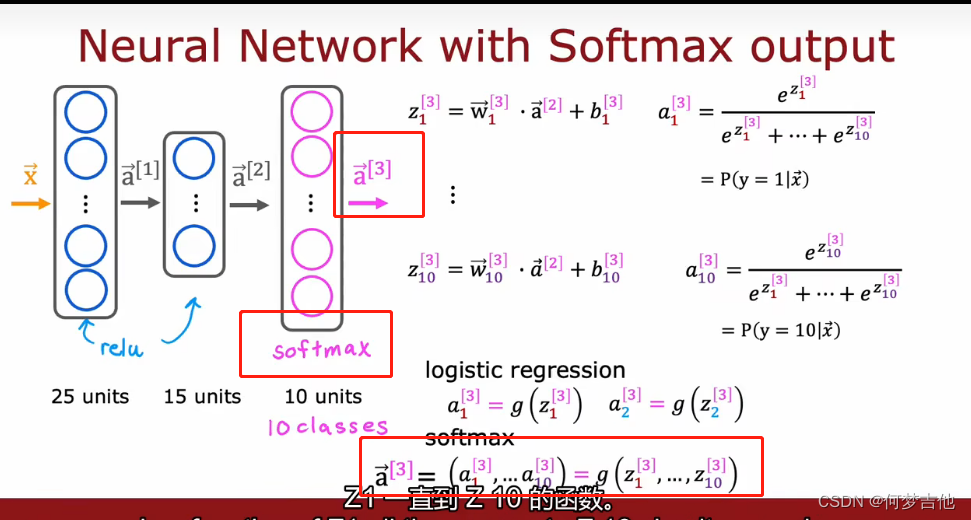输出层也叫作softmax层，输出的K维向量a，中的每一个分量都与z1-z10有关系，这个和之前学的不太一样

7.5.2 softmax 改进实现，更加精确

理解不同的计算方式的精度是不同的，有的会在计算机存储过程中伴随值精度的损失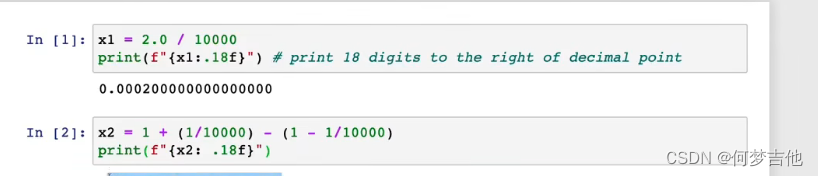
在这里插入图片描述
当output layer 层为sigmoid 函数，精确度不太影响，但当是softmax激活函数时，需要改进！

之所以是linear是因为下面设定为True之后，softmax不再单独计算，只在计算cost时嵌入内部一起算了。这样输出层只会输出Z的值，不再带入softmax计算了

可以避免在计算 softmax 操作时出现数值不稳定的情况，同时也可以简化代码实现。如果不将 from_logits 设置为 True，则在进行 softmax 转换时需要手动对 logits 进行指数运算和除法，这样的实现较为繁琐。

7.5.3 多标签分类问题

在这里插入图片描述
输出值y是一个向量，而不是一个数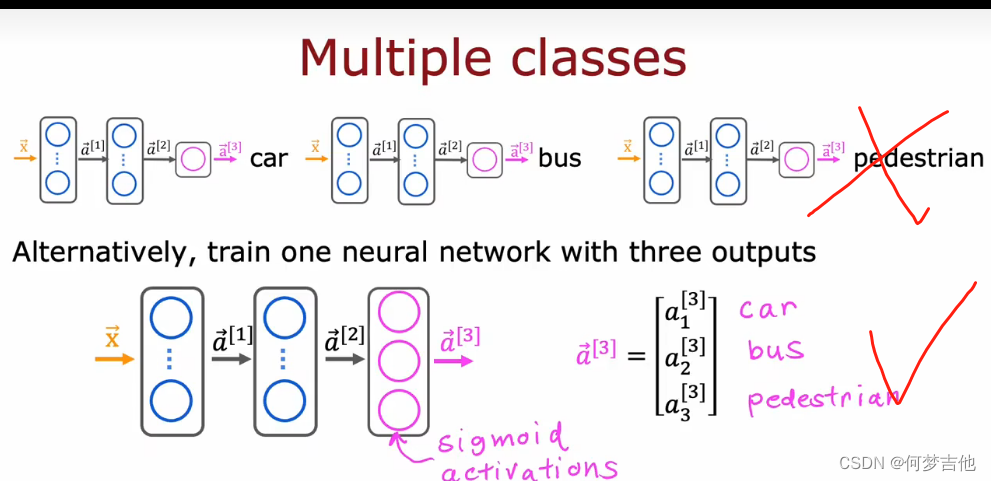

不能用softmax，因为比如既有人又有车无法处理，对每个分量用sigmoid

7.6 高级优化方法

7.6.1 Adam 算法自适应距估计 ——自动调节学习率大小

在这里插入图片描述
需要一个默认的学习率，建议可以选一个大点，一个小点的多试

7.7 其他网络层的类型

dense layer 密集层就是全连接层一种隐藏层，其中的每个节点均与下一个隐藏层中的每个节点相连。
convolutional layer 卷积层例子：心电图识别，判断是否有心脏病，二分类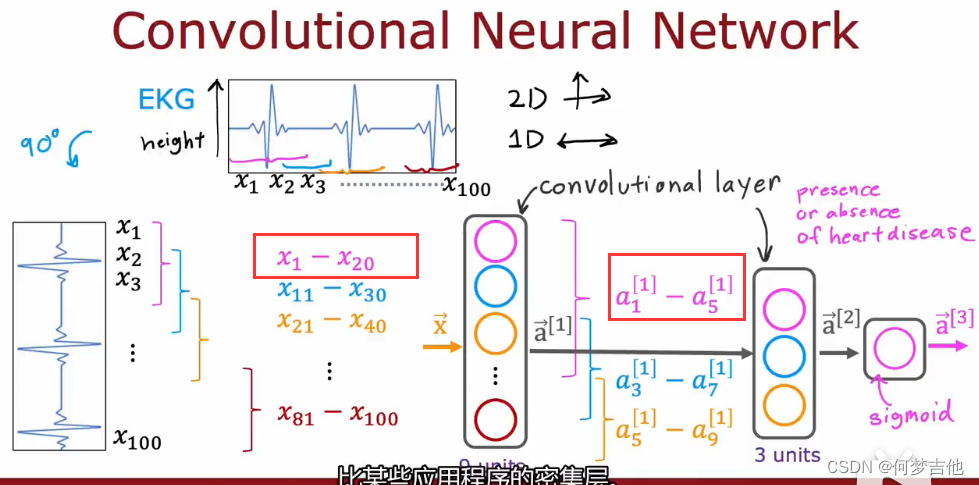需要考虑的参数：单个神经元应该观察的输入窗口有多大？一层应该有几个神经元？

八、细节

8.1 使用测试集评估模型性能

划分训练集和测试集 8 2 7/3
计算Jtest 、Jtrain 衡量模型在测试集合训练集上的、不包括正则化项

对于线性回归问题：

在这里插入图片描述
2. 分类问题

Jtest(W,b)是测试集中被错误分类的部分。
Jtrain(W,b)是训练集中被错误分类的部分。

8.2 模型选择 \ 交叉验证集

一旦参数w,b被拟合到训练集，训练误差Jtrain(W,b)就可能低于实际的泛化误差。
Jtest(W,b)比Jtrain(W,b)能更好地估计模型对新数据的概括程度。
在这里插入图片描述
1 训练集train用来训练参数w和b，而测试集test用来选择多项式模型（即参数d），训练集不能评估w和b的好坏，类似的测试集也不能用来评估参数d的好坏。w，b与d一样都是经过学习得到的，那么当然都会存在一些问题。
2. 根据测试集误差选择的参数d，所以可能是乐观估计。一个只考虑到训练集误差Jtrain，一个只考虑到测试集误差Jtest，都不全面，所以是乐观预测

交叉验证集、开发集、验证集 dev set 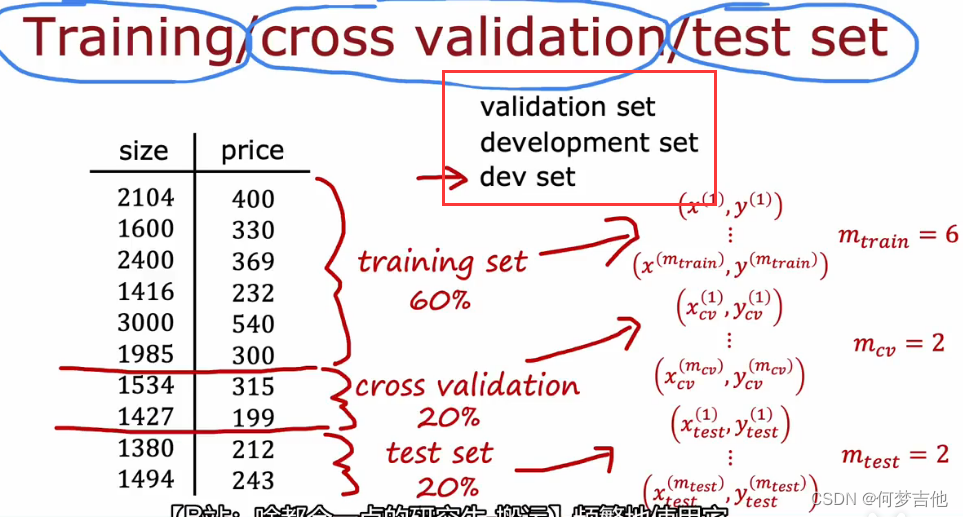validation error 交叉验证误差

理解：先通过训练集拟合w,b. 然后通过交叉集选择出最优的模型也即参数d，最后用选择出来的模型在测试集中估计泛化能力
就是一个训练参数wb，一个挑选最合适的一个模型，test用来算误差（敲定最终模型，才能在test集中评估）

8.3 偏差方差 bias variance

计算Jtrain Jcv 比较大小，来判断算法是否高偏差、高方差

在统计学和机器学习中，高方差（high variance）通常指模型对训练数据的过度拟合，从而导致在新的、未见过的数据上表现较差的情况。在机器学习中，一个常见的目标是在高偏差和高方差之间取得平衡，以达到最佳的泛化性能。（ChatGPT）

从Jtrain 和Jcv 大小来理解偏差和方差

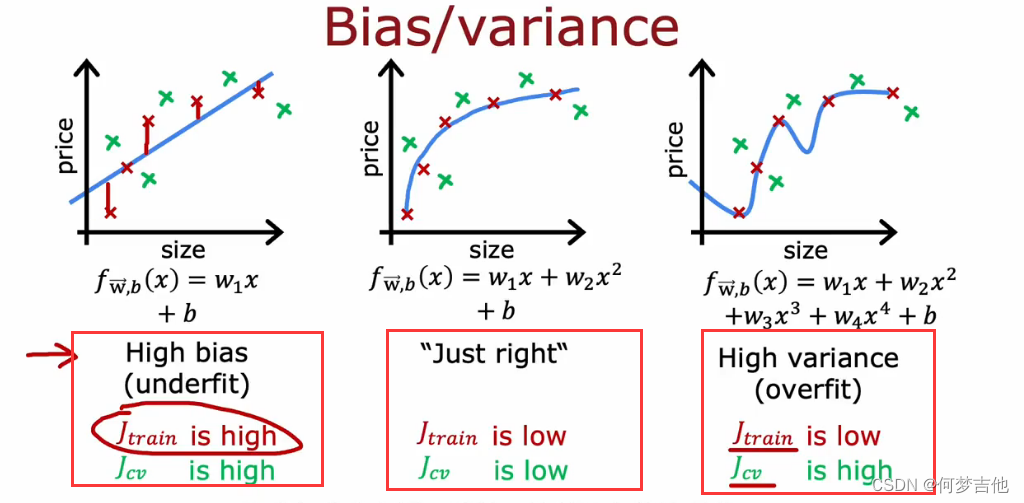
在这里插入图片描述

另一个角度高次项大小当高次项越来越大时候，Jtrain会下降；次项太小，欠拟合，jcv很大在交叉验证集上效果不好，当次项太大，过拟合，jcv也很大，在中间

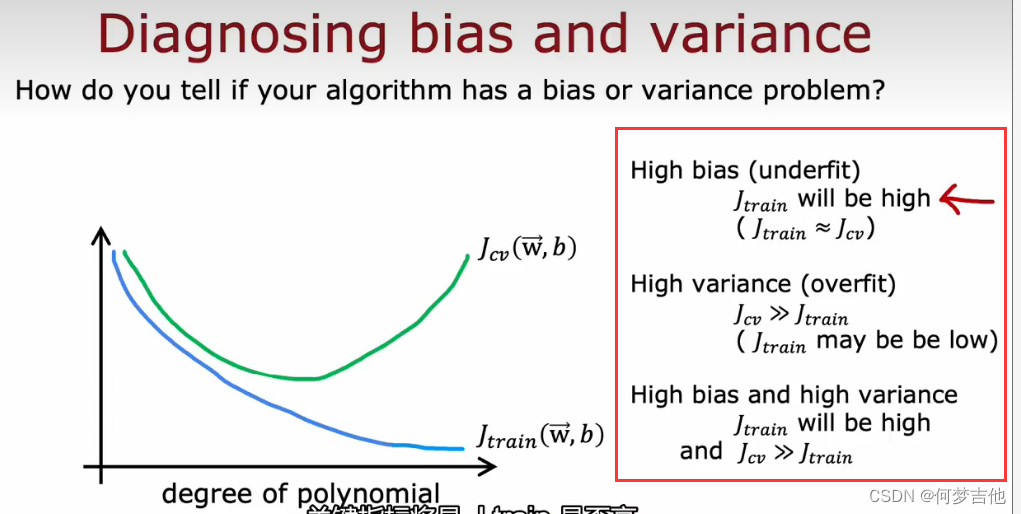
在神经网络拟合过程中，高方差和高偏差可能会同时存在

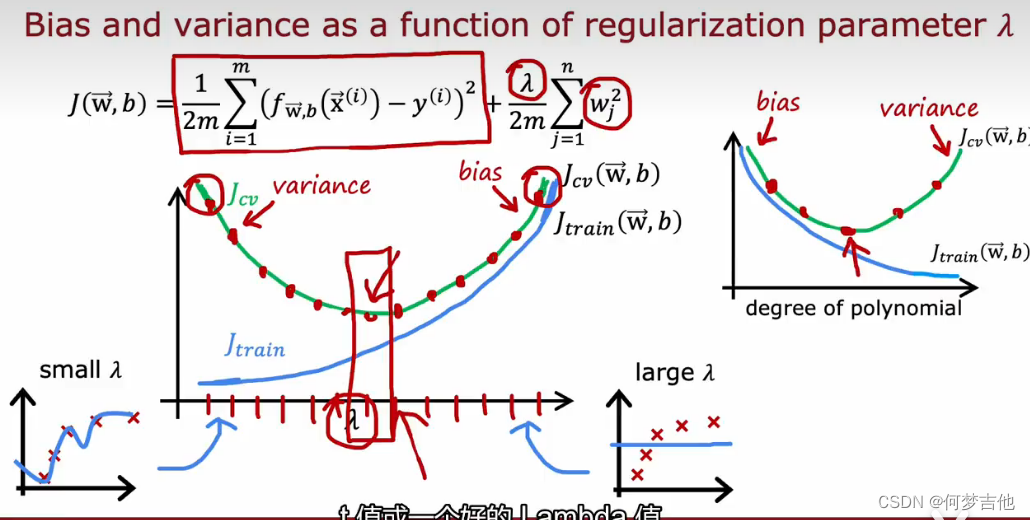
8.4 正则化参数

     l 
    
   
     a 
    
   
     m 
    
   
     d 
    
   
     a 
    
   
  
    lamda 
   
  
lamda对 偏差、方差影响 | 如何利用 交叉验证 选则正则化参数lamda

正则化如何影响算法的偏差和方差，什么时候应该使用正则化？

当lamda 很大，算法视图保持w2越小，导致参数很接近0，最后模型就会接近fx = b ，欠拟合
当lamda很小，极端点为0，就变成了没有正则化化的损失函数J，会过拟合
如何选择lamda ？，利用交叉验证

如何选择lamda，利用交叉验证集Jcv

在这里插入图片描述

类似模型选择，从lamda=0开始计算Jtrain拟合出wb参数，然后在交叉验证集cv上计算Jcv误差，每次把lamda变大2倍，选择最小的，最后在test测试集评估Jtest，达到泛化

从Jcv -Jtrain —— lamda 图像理解

在这里插入图片描述

8.5 指定一个用于性能评估的基准 baseline =》判断是否有高偏差、高方差的情况

例子语音识别

基准baseline performance 和Jtrain 之间的距离，可以判断是否有一个高偏差bias问题
Jtrain 和Jcv之间的距离可以判断是否有一个高方差variance

当Jtrain>>Jcv ,有高方差

8.6 通过学习曲线=》判断是否有高偏差、高方差

妈的，写了，忘记保存，全没了！！！！！！

8.7 误差分析

垃圾邮件分类例子人工分析错误分类的100封邮件（如果很大，就按比例抽取）找出影响大的类别，专注于添加更多典型的错误的例子！

8.8 添加更多数据的技巧

数据增强

对于图像数据，扭曲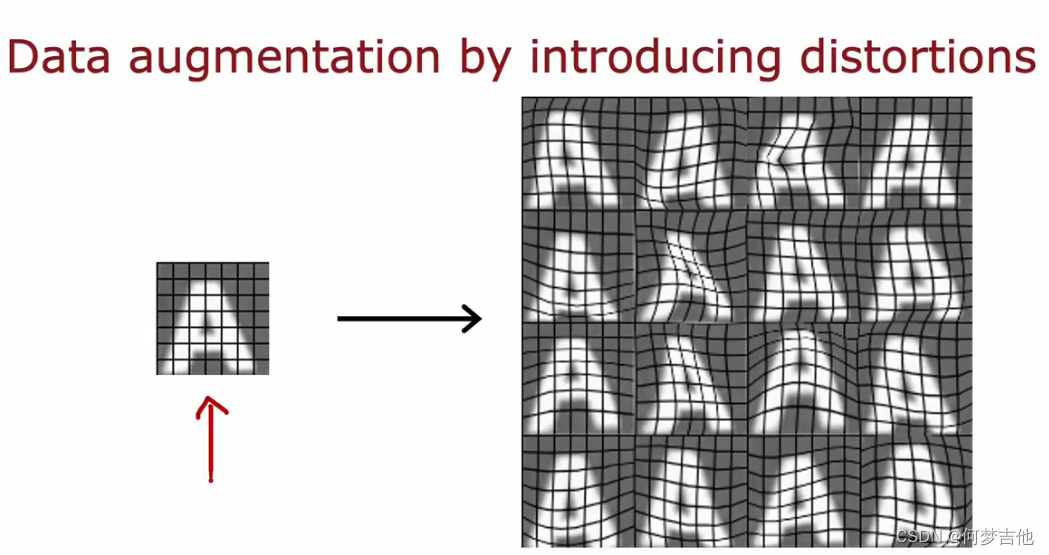
在这里插入图片描述
对于音频数据、添加噪声

数据合成

一般用于计算机视觉干扰
在这里插入图片描述

有一些时候，关注数据是帮助算法提高性能的有效方法！
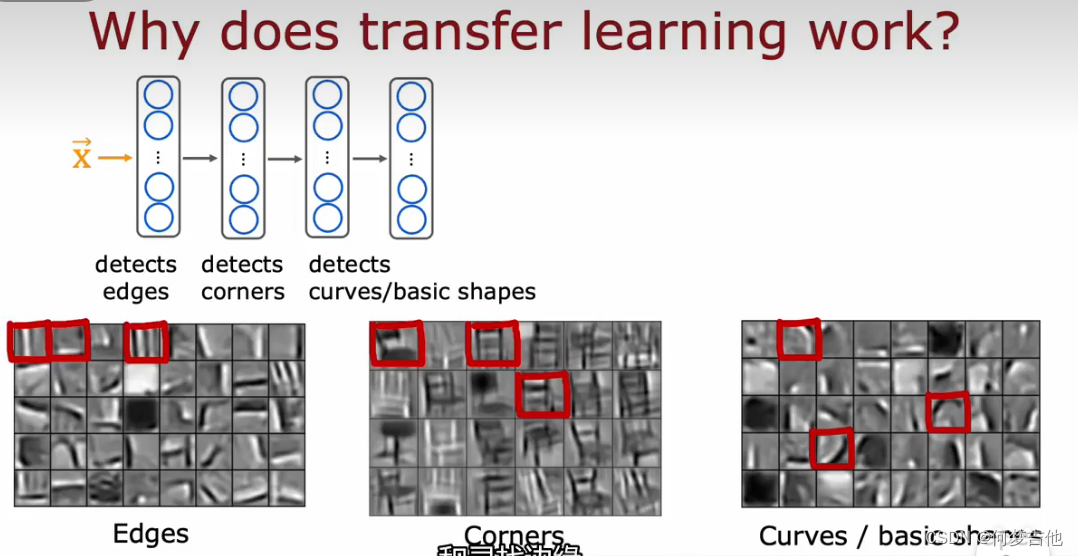
在这里插入图片描述

8.9 迁移学习 transfer learning（监督预训练）

作用：让你用来自不同任务的数据来解决当前的任务

例子：把动物识别迁移到0-9数字识别

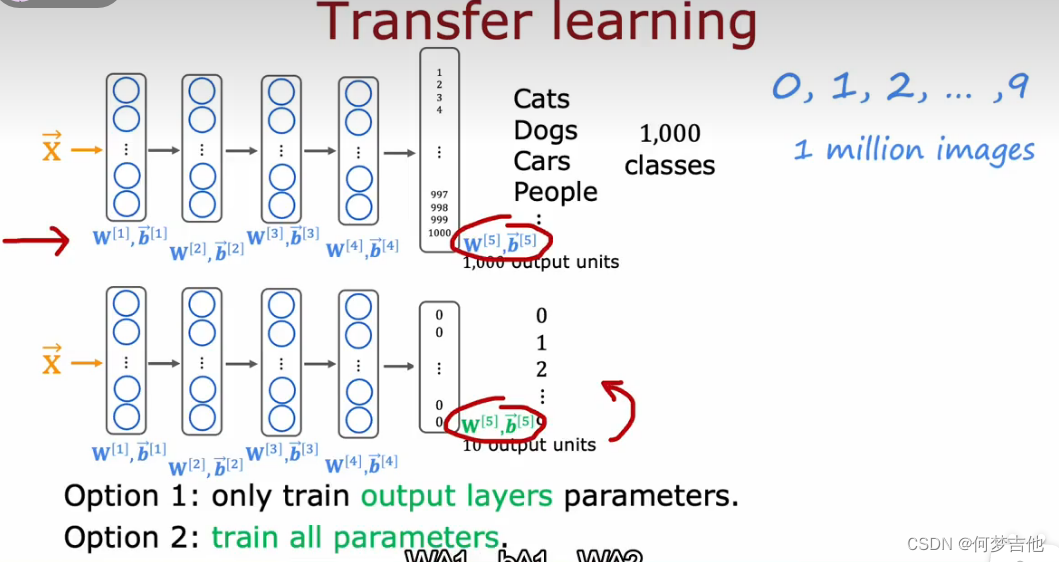
微调方法一（训练集很小）前4个参数仍然保留，只需要更新输出层的参数，利用gd 或者adam优化算法来最小化代价函数
微调方法二（训练集很大）重新训练所有参数，但前四层的参数还是用上面的值作为初始值！

1.因为两个网络的本质都是图像分类，所以在隐藏层的大部分工作都是相似甚至一样的
2.所以直接把第一个网络的隐藏层拿过来用，对输出层重新训练就能实现新的功能
3.相当于螺丝刀的刀柄都是一样的，但把十字刀刀头换成一字刀作用就不一样了
下面的图可以帮你理解迁移学习的原理：

神经网络每一层训练它学会检测边缘、拐角、曲线和基本形状

预训练监督预训练supervised pretraining：首先在大型数据集上进行训练，然后在较小的数据集上进行进行参数微调（fine tuning）利用已经初始化的或者从预训练模型获取的参数，运行gd，进一步进行微调权重，以适应手写数字识别任务

什么是微调？可以这样理解，你下载了别训练好的神经网络，自己使用更小的数据集50 100张等，来训练这个网络

8.10倾斜数据集的误差指标 Error metrics for skewed datasets

数据倾斜某个类别的样本数只有另一个类别的1/10，这个数据集就是倾斜的。这种情况也常常出现在诸如诈骗检测、医学诊断、罕见事件预测等领域中，因为这些问题中正例（positive）的数量通常比负例（negative）少得多。
例子：罕见症预测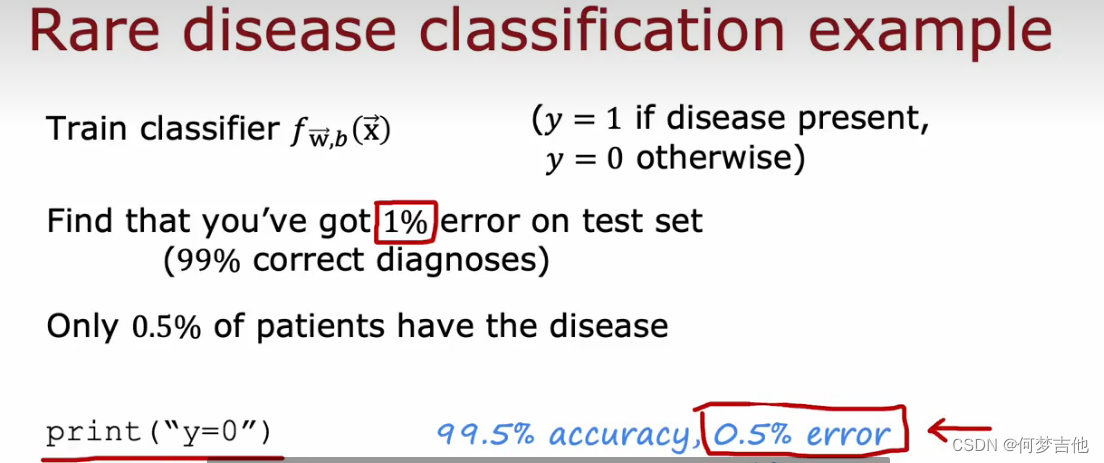使用不同的误差量度，而不仅仅是分类误差!

8.10.1 精确率和召回率 Precision/ recall 、混淆矩阵

对于这个罕见病识别的例子：
精确率：就是预测为阳性的病人中真正为阳性的人的比例（找的对 ）
召回率：在所有患有罕见病的人中，我们真正正确检测的比例（阳了的人，有多少被正确的检测出来了，找的全）
在这里插入图片描述

在医学诊断领域中，通常更关注召回率，因为漏诊罕见病患者可能会导致严重后果

混淆矩阵
Actual PositiveActual NegativePredicted PositiveTPFPPredicted NegativeFNTN
左上角是真正例（True Positive，TP），表示模型正确预测出了正例；
右上角是假正例（False Positive，FP），表示模型将负例错误预测为正例；
左下角是假反例（False Negative，FN），表示模型将正例错误预测为负例；
右下角是真反例（True Negative，TN），表示模型正确预测出了负例。
精确率（Precision）是指被分类器正确识别为正例的样本数占所有分类器判定为正例的样本数的比例，即： P r e c i s i o n = T P T P + F P Precision=\frac{TP}{TP+FP} Precision=TP+FPTP 其中，TP表示真正例（True Positive），即实际为正例且被分类器正确识别的样本数；FP表示假正例（False Positive），即实际为负例但被分类器错误识别为正例的样本数。
召回率（Recall）是指被分类器正确识别为正例的样本数占所有实际为正例的样本数的比例，即： R e c a l l = T P T P + F N Recall=\frac{TP}{TP+FN} Recall=TP+FNTP 其中，TP表示真正例（True Positive），即实际为正例且被分类器正确识别的样本数；FN表示假负例（False Negative），即实际为正例但被分类器错误识别为负例的样本数。

8.10.2 精确率（找的对）和召回率（找的全）的权衡、F1score

我们将患病的样本标记为正类，未患病的样本标记为负类。在这种情况下

1. 手动选择一个阈值来权衡精度和召回率

如果治病的代价很大，患病后果不难么严重，只在我们十分有把握的情况下去预测y=1，设置更高的阈值（如0.7），这样precision会增加（因为是十分有把握，找的对的概率大了）；recall会减少（假阴性FN的结果增多，即实际患病的样本被错误地判断为未患病），

如果我们将阈值设置得比较高，模型会更倾向于将未患病的样本判断为负类，这样会导致假阴性的结果增多，即实际患病的样本被错误地判断为未患病，从而导致召回率recall的下降。但是，由于正类被错误地预测为负类的情况减少了，所以精度precision会随之提高。

另一方面，如果我们不想漏掉罕见病病例，治疗风险不大，但不治疗的结果很坏，可以减低阈值，结果跟上面相反

在这里插入图片描述

总结：
我们需要根据具体情况来选择更注重精确率还是召回率。对于不同的应用场景，我们可能会有不同的需求。如果我们更关心查准率，那么就需要选择更高的精确率阈值，这样可以减少假阳性的情况，提高预测结果的准确性；如果我们更关心查全率，那么就需要选择更低的精确率阈值，这样可以减少假阴性的情况，提高预测结果的召回率

高精确率：判定为true的置信度高
高召回率：判定为false的置信度高
置信度是指一个统计推断中，对于一个参数或者假设所得到的推断结果的可信程度或者确定性程度。置信度通常使用置信区间来度量，表示参数或假设在一定置信水平下的可能取值范围。
置信度高表示推断所得的结果越可信，即在一定置信水平下，得到的置信区间越小，说明参数或假设的可能取值范围越小，结果越精确可靠。例如，如果某个样本的置信区间为[2, 6]，则在95%的置信水平下，该样本的真实值有95%的可能在区间[2, 6]内。如果置信度更高，比如99%的置信水平，则样本的真实值有99%的可能在更小的区间内，如[2.5, 5.5]。

阈值的选择会直接影响模型的预测结果，其中较高的阈值会使模型更倾向于将样本归类为负类，而较低的阈值则会使模型更倾向于将样本归类为正类。
举个例子，假设有1000个样本，其中只有10个是患病的正样本。如果我们将阈值设置得很高，比如说0.95，那么模型可能只会将其中一个正样本预测为正类，而将其余9个正样本都判断为负类。这样，精度会变得非常高，达到99%以上，但是召回率只有10%。相反，如果我们将阈值设置得很低，比如说0.1，那么模型可能会将大部分样本都预测为正类，从而召回率很高，但是精度会很低，因为大多数预测为正类的样本实际上是负样本。因此，在设置阈值时需要平衡召回率和精度，根据实际应用情况选择合适的阈值。

1. F1 score 自动权衡精度和召回率，

F1 score（F1值）是一种综合评价分类器性能的指标，结合了分类器的准确率和召回率。它是准确率和召回率的调和平均数（取平均值的方法，更强调较小的值），通常用于评估二元分类器的性能。

F1 score 的计算公式为：

      F 
     
    
      1 
     
    
      s 
     
    
      c 
     
    
      o 
     
    
      r 
     
    
      e 
     
    
      = 
     
    
      2 
     
     
      
      
        P 
       
      
        r 
       
      
        e 
       
      
        c 
       
      
        i 
       
      
        s 
       
      
        i 
       
      
        o 
       
      
        n 
       
      
        ∗ 
       
      
        R 
       
      
        e 
       
      
        c 
       
      
        a 
       
      
        l 
       
      
        l 
       
      
      
      
        P 
       
      
        r 
       
      
        e 
       
      
        c 
       
      
        i 
       
      
        s 
       
      
        i 
       
      
        o 
       
      
        n 
       
      
        + 
       
      
        R 
       
      
        e 
       
      
        c 
       
      
        a 
       
      
        l 
       
      
        l 
       
      
     
    
   
     F1 score=2\frac{Precision*Recall}{Precision+Recall} 
    
   
 F1score=2Precision+RecallPrecision∗Recall

在计算 F1 score 时，精确率和召回率对结果的贡献是一样的。因此，F1 score 强调了精确率和召回率同等重要。
当精确率和召回率差异较大时，F1 score 的值会受到最小值的影响。例如，当精确率很低但召回率很高时，F1 score 的值会受到精确率的影响而降低，因为 F1 score 考虑了两者的平均值。

8.11 机器学习项目完整的周期

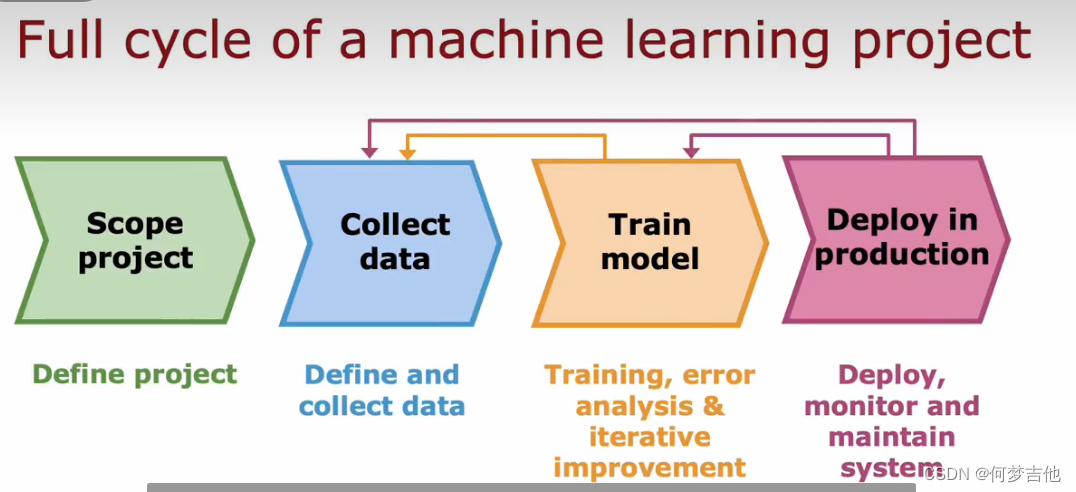
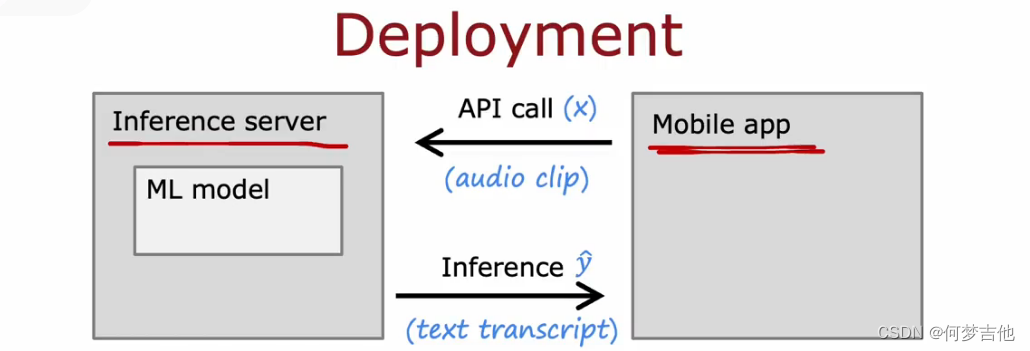
在这里插入图片描述

MLOps 机器学习操作
MLOps将机器学习项目管理的方法与软件工程方法相结合，以建立高效、可重复、可维护的机器学习系统。这种方法强调持续学习、持续优化和自动化，以确保机器学习模型能够在不断变化的环境中保持最佳状态。

九、决策树

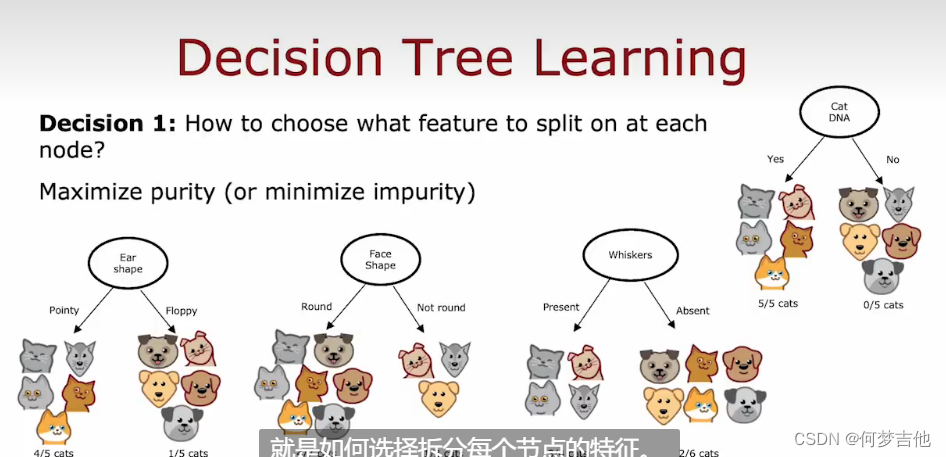
决策1：如何选择在每个节点上分割什么特征？****最大限度地提高纯度（或最小限度地减少不纯）。
决策2：什么时候停止拆分？1. 当一个节点是一个单一类时2. 当拆分一个节点会导致树超过最大的深度3. 当纯度分数的改进低于一个阈值（获得的信息增益很小小于阈值）4. 当一个节点中的例子数量低于一个阈值

在这里插入图片描述

9.1 衡量纯度、熵entropy、 Gini指数

在这里插入图片描述

熵（Entropy）通常用于衡量样本集合的不确定性和纯度，也可以理解为样本集合中随机选取一个样本，其所包含的信息量，混乱程度。

以二分类问题为例，假设样本集合

     D 
    
   
  
    D 
   
  
D中包含正例样本数为 
 
  
   
   
     ∣ 
    
    
    
      D 
     
    
      + 
     
    
   
     ∣ 
    
   
  
    |D_+| 
   
  
∣D+∣，反例样本数为 
 
  
   
   
     ∣ 
    
    
    
      D 
     
    
      − 
     
    
   
     ∣ 
    
   
  
    |D_-| 
   
  
∣D−∣，则**样本集合 
  
   
    
    
      D 
     
    
   
     D 
    
   
 D的熵可以表示为（类似逻辑回归 二分类问题用Binary Cross Entropy二元交叉熵损失函数）：**


  
   
    
    
      Ent 
     
    
      ⁡ 
     
    
      ( 
     
    
      D 
     
    
      ) 
     
    
      = 
     
    
      − 
     
     
     
       p 
      
     
       + 
      
     
     
      
      
        log 
       
      
        ⁡ 
       
      
     
       2 
      
     
     
     
       p 
      
     
       + 
      
     
    
      − 
     
     
     
       p 
      
     
       − 
      
     
     
      
      
        log 
       
      
        ⁡ 
       
      
     
       2 
      
     
     
     
       p 
      
     
       − 
      
     
    
   
     \operatorname{Ent}(D) = -p_+\log_2 p_+ - p_-\log_2 p_- 
    
   
 Ent(D)=−p+log2p+−p−log2p−

其中，

      p 
     
    
      + 
     
    
   
  
    p_+ 
   
  
p+和 
 
  
   
    
    
      p 
     
    
      − 
     
    
   
  
    p_- 
   
  
p−分别表示样本集合中正例和反例的比例，即：


  
   
    
     
     
       p 
      
     
       + 
      
     
    
      = 
     
     
      
      
        ∣ 
       
       
       
         D 
        
       
         + 
        
       
      
        ∣ 
       
      
      
      
        ∣ 
       
      
        D 
       
      
        ∣ 
       
      
     
    
      , 
     
     
     
     
       p 
      
     
       − 
      
     
    
      = 
     
     
      
      
        ∣ 
       
       
       
         D 
        
       
         − 
        
       
      
        ∣ 
       
      
      
      
        ∣ 
       
      
        D 
       
      
        ∣ 
       
      
     
    
   
     p_+ = \frac{|D_+|}{|D|},\quad p_- = \frac{|D_-|}{|D|} 
    
   
 p+=∣D∣∣D+∣,p−=∣D∣∣D−∣

可以发现，当正例和反例比例相等时，即

      p 
     
    
      + 
     
    
   
     = 
    
    
    
      p 
     
    
      − 
     
    
   
     = 
    
   
     0.5 
    
   
  
    p_+=p_-=0.5 
   
  
p+=p−=0.5时，此时的熵取最大值 
 
  
   
   
     1 
    
   
  
    1 
   
  
1，表明此时样本集合最不确定，**样本集合越不纯，熵值越**大；而当样本集合中只包含一类样本（即纯样本集合）时，**熵值为 
  
   
    
    
      0 
     
    
   
     0 
    
   
 0，表明此时样本集合已经完全确定，很纯**。

在决策树算法中，熵常常被用来选择最优划分点，即在样本的某个特征上根据熵的变化选取最优的划分点，使得划分后的样本子集中的熵最小。

Gini指数

Gini指数是一种用于衡量数据集纯度的指标，通常用于决策树算法中。在分类问题中，假设有K个类别，数据集D中第k类样本所占的比例为

      p 
     
    
      k 
     
    
   
  
    p_k 
   
  
pk，则Gini指数的计算公式如下：


  
   
    
    
      G 
     
    
      i 
     
    
      n 
     
    
      i 
     
    
      ( 
     
    
      D 
     
    
      ) 
     
    
      = 
     
     
     
       ∑ 
      
      
      
        k 
       
      
        = 
       
      
        1 
       
      
     
       K 
      
     
     
     
       p 
      
     
       k 
      
     
    
      ( 
     
    
      1 
     
    
      − 
     
     
     
       p 
      
     
       k 
      
     
    
      ) 
     
    
   
     Gini(D) = \sum_{k=1}^{K}p_k(1-p_k) 
    
   
 Gini(D)=k=1∑Kpk(1−pk)

Gini指数衡量的是从数据集D中随机选取两个样本，其类别不一致的概率，因此Gini指数越小，数据集的纯度越高，分类效果越好。与熵类似，Gini指数也是在0到1之间取值，取值越小表示数据集的纯度越高。

在决策树算法中，选择划分特征时，通常会计算每个特征的Gini指数或信息增益，以选取最佳的划分特征。

9.2 信息增益

在这里插入图片描述

p1表示样本集合中正例也即猫的比例，wleft指的是占样本的权重，p1 left 代表左枝正例的比例

在决策树算法中，我们希望通过选择最优特征来划分数据集，从而使划分后的数据集更加纯净，即熵减少。而这个熵减少的量就被称为信息增益

信息增益是一种用于衡量一个特征对分类任务的贡献程度的指标，通常用于决策树算法中。在决策树算法中，我们需要在每个节点上选择一个特征，使得选定特征后能够最大程度地提高数据的纯度（即分类的准确性）。信息增益的计算方法是：首先计算数据集的熵，然后计算选定特征后的条件熵，两者相减即为该特征的信息增益。信息增益越大，代表该特征对分类任务的贡献越大。

9.3 独热编码One-hot

前面的例子，每个特征只能取两个不同的值，如胡子有、无
，耳朵的尖、椭圆，对于有两个以上的离散值的特征，使用one hot编码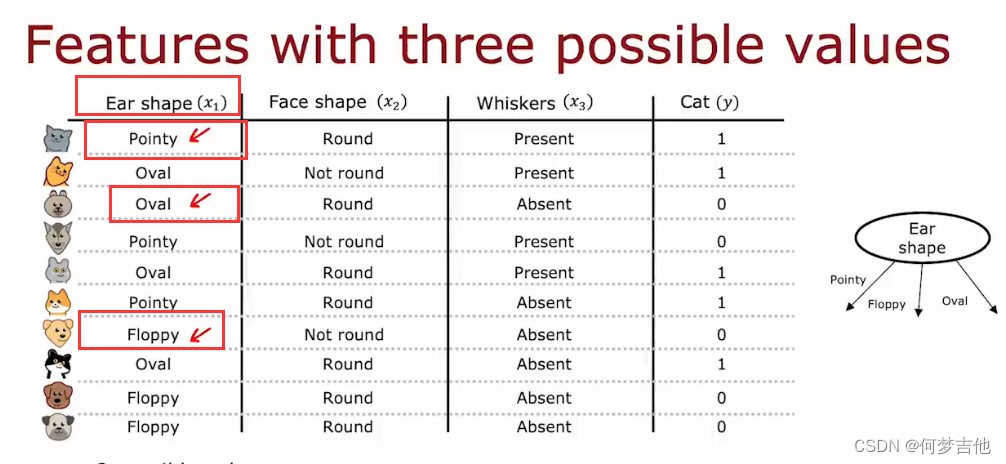
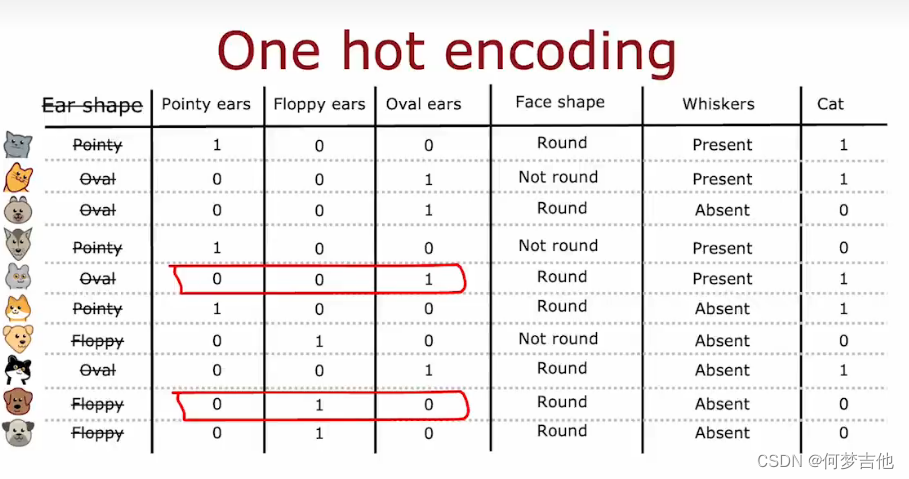
在这里插入图片描述

之所以叫one hot ，因为这些特征总有一个取1，

不仅仅适用于决策树，可以对分类特征进行编码，以便作为输入送入神经网络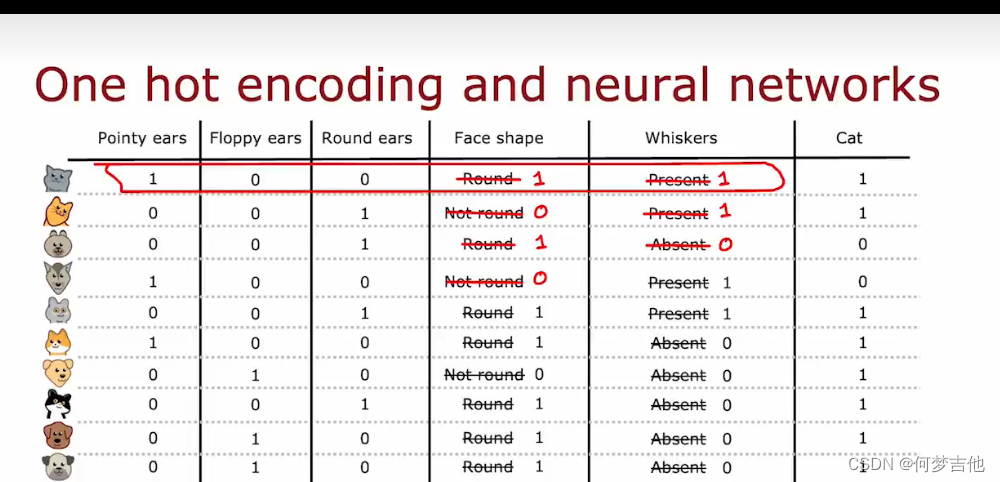
在这里插入图片描述

9.4 连续值特征

新增体重特征，是连续值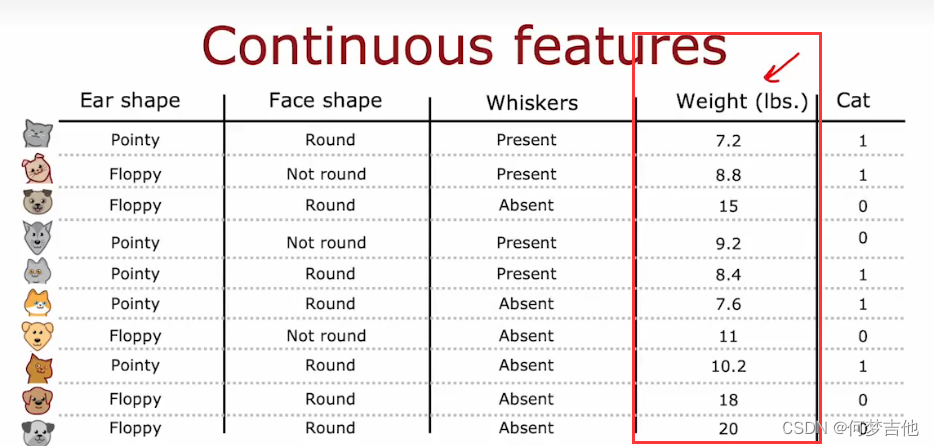
在这里插入图片描述
将特征划分，考虑不同的值，计算分隔后的信息增益，选择一个最好的，能获得最好信息增益的那个！

一般的做法：对所有的样本排序，根据体重大小排序，取中点值，作为这个阈值的候选值

9.5 回归树 regression tree

泛化到回归问题，预测一个数字，而不是分类问题
例子：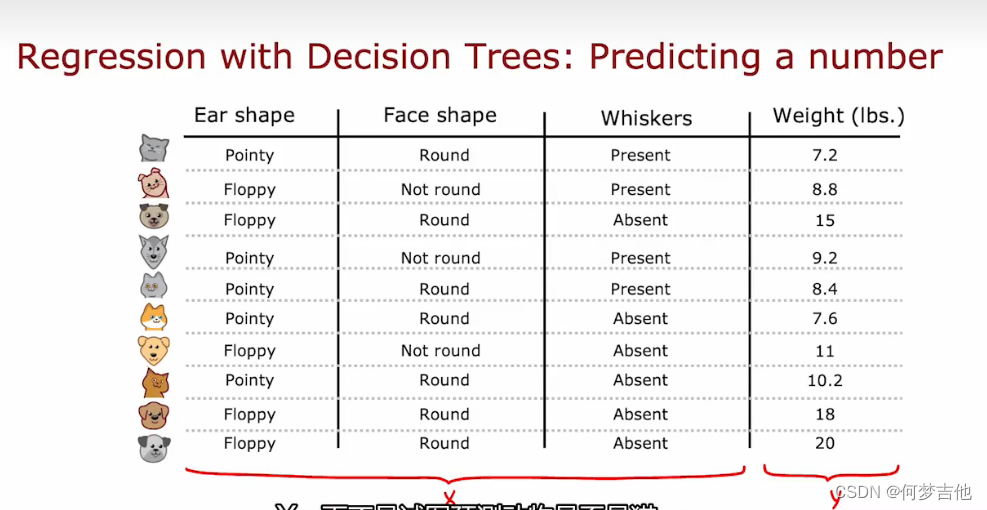
在这里插入图片描述
用一个决策树来回归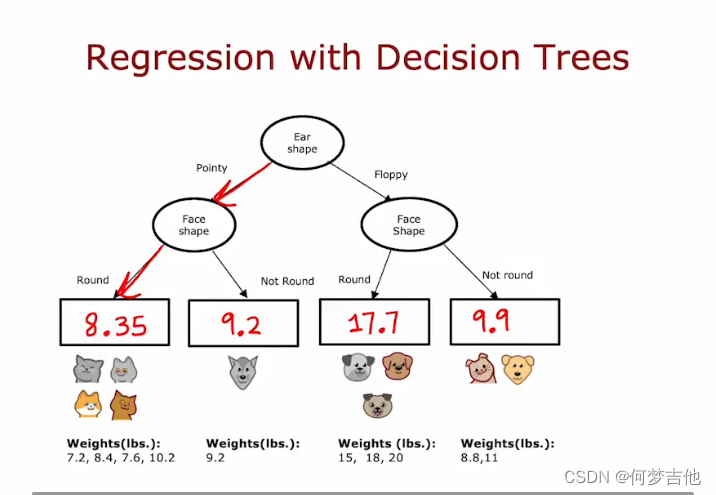

重新选择划分的标准，重新生成

在划分时，不去计算信息增益，不去衡量纯度，不如减少数据的方差，类似信息增益，我们测量的是方差的减小，选择方差减少最大的那个特征分类标准
在这里插入图片描述

9.6 树集合 Tree ensemble

单个决策树受到数据变化的影响很大，导致不同的划分，形成可能不同的树，让算法的鲁棒性变低；
使用树集合，让每一颗树投票。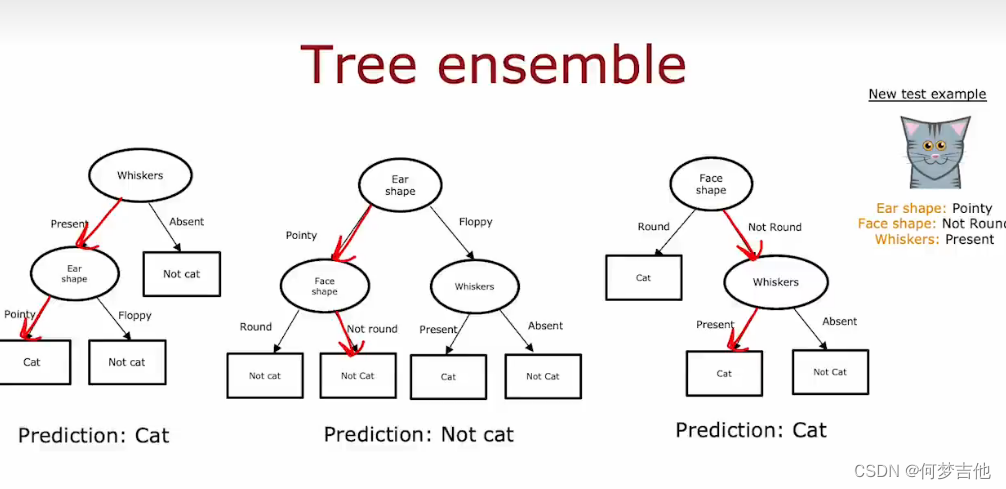
在这里插入图片描述

9.6.1 有放回抽样sampling with replacement （构造多个随机的训练集）

构建树集合的方式如下：构建多个随机的训练集，都与我们最初的训练集略有不同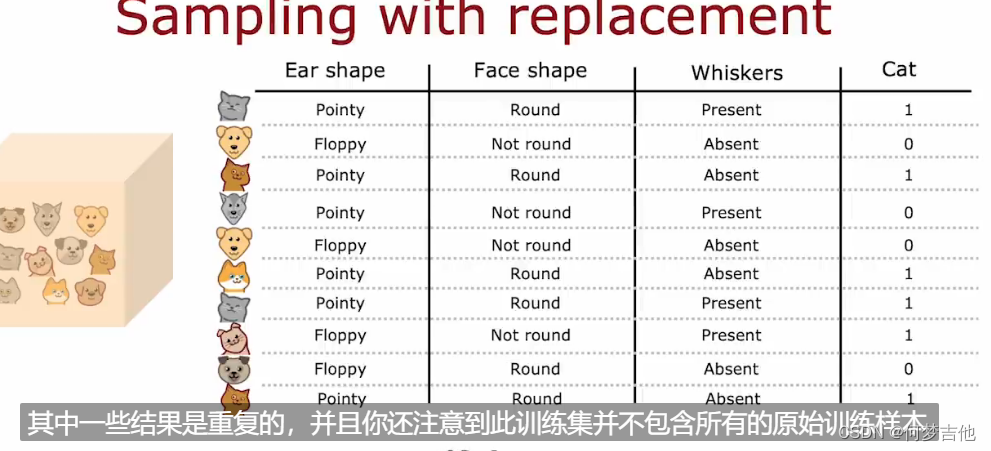
在这里插入图片描述

9.6.2随机森林算法

在这里插入图片描述
在这个基础上，随机选k个特征值进行决策树的构建

在每个节点上，当选择用于分割的特征时，如果有n个特征，则从特征中随机挑选一个子集，子集大小为k k<n，选择k个特征作为允许的特征；然后从这k个特征中选收获最大信息增益的特征作为分割特征

随机森林是一种集成学习算法，它由多个决策树组成，每个决策树之间相互独立。随机森林的构造方法如下：

随机选取n个样本作为训练集，对于每个样本，随机选取k个特征进行决策树的构建。通常情况下，n取样总数的70%到80%，k取特征总数的平方根。
对于每个节点，随机选取k个特征进行划分，并在选取的特征中找到最优划分特征。这里的最优划分是通过计算信息增益或Gini系数等指标得出的。
重复步骤1和步骤2，构建多棵决策树。
预测时，将新数据输入到每个决策树中，得到每棵树的预测结果，然后根据投票法或平均值等方法，得到随机森林的最终预测结果。

随机森林算法具有良好的泛化性能和抗噪性能，通常被用于分类和回归任务。

9.6.3 XGBoost

理解boost的思想我们关注的是我们还没做好的地方，在构建下一个决策树时，把更多的注意力放在做得不好的例子上，不是以相等的(1/m)概率从所有的例子中选取，而是更有可能选取以前训练的树所错误分类的例子。

boosting 刻意练习 deliberate practice

在这里插入图片描述

XGBoost extreme gradient boosting 极端梯度提升

在这里插入图片描述

XGBoost的训练过程是一个逐步迭代的过程。它通过不断训练多棵决策树，并使用梯度下降来对每棵树的权重进行优化，以最小化损失函数。
具体来说，XGBoost在构建每棵树时，会先构建一个根节点，然后逐步将数据集分配到子节点中。每次分配数据集时，XGBoost都会根据一个指定的评价函数来选择最佳的特征进行分裂，并计算每个子节点的权重。通过这种方式，XGBoost可以在不断迭代中构建多棵树，并综合它们的预测结果来提高模型的准确率。

9.7 何时使用决策树、神经网络

决策树

决策树可以很好处理表格数据（结构化数据）
训练很快
小型的决策树具有可解释性

神经网络

适用于所有类型的数据，表格和非结构化数据
可能比较慢
可以迁移学习、预训练

在这里插入图片描述

十、无监督学习

10.1 聚类 clustering

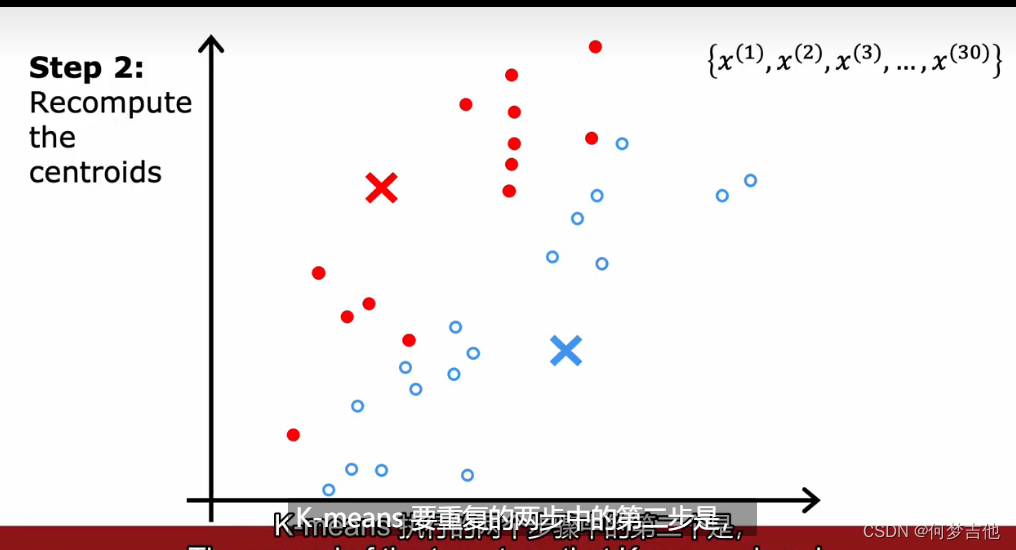
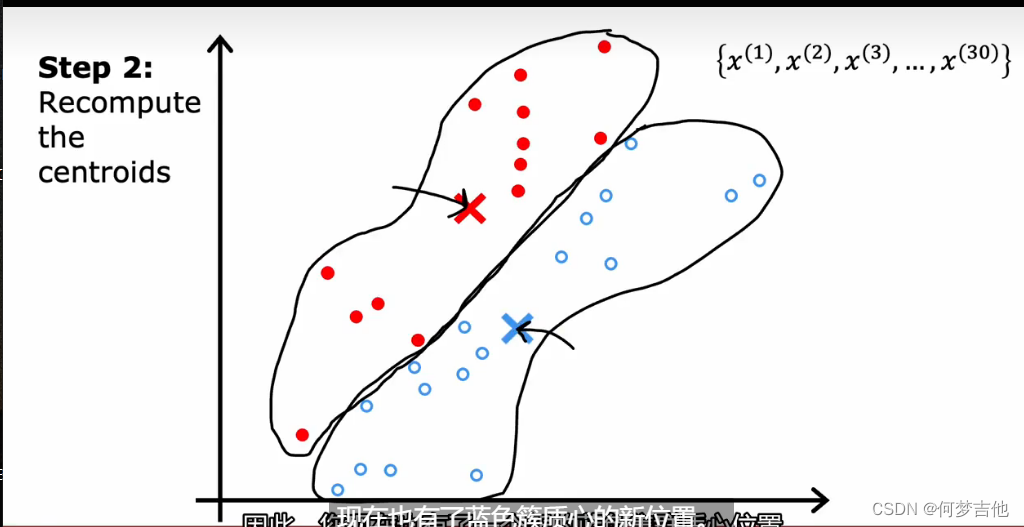
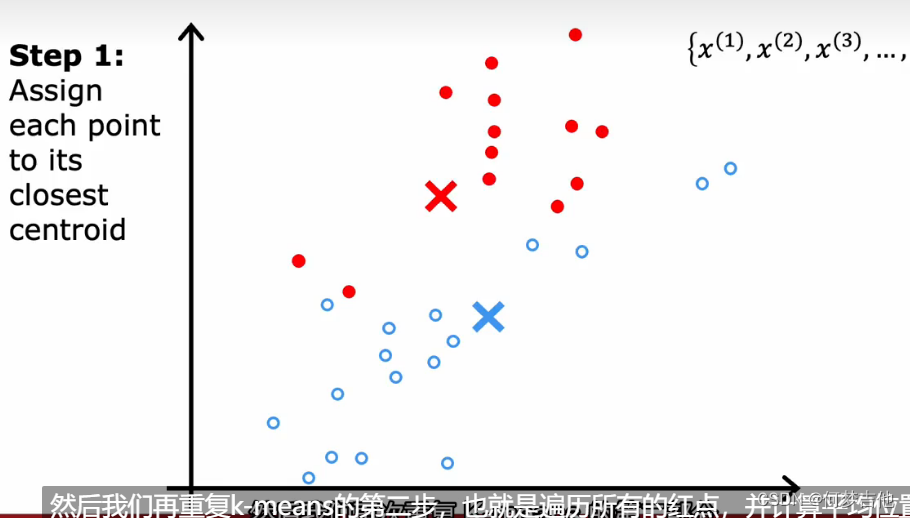
10.1.1 K-means算法原理

理解K-means如何工作关键两个步骤：第一步，把每个点分配给簇质量心，分配给离它最近的簇质心；第二步，把每个簇质心分配给它所有点的平均位置;直到簇质心没有变化
算法

计算距离采用L2范数也称为欧几里得范数，是指向量各元素的平方和再开方，它可以用来衡量向量的大小。在二维空间中，向量

      ( 
     
    
      x 
     
    
      , 
     
    
      y 
     
    
      ) 
     
    
   
     (x, y) 
    
   
 (x,y)的L2范数为 
  
   
    
     
      
       
       
         x 
        
       
         2 
        
       
      
        + 
       
       
       
         y 
        
       
         2 
        
       
      
     
    
   
     \sqrt{x^2 + y^2} 
    
   
 x2+y2。在机器学习中，L2范数常用于正则化技术中，可以限制模型的复杂度，防止过拟合。

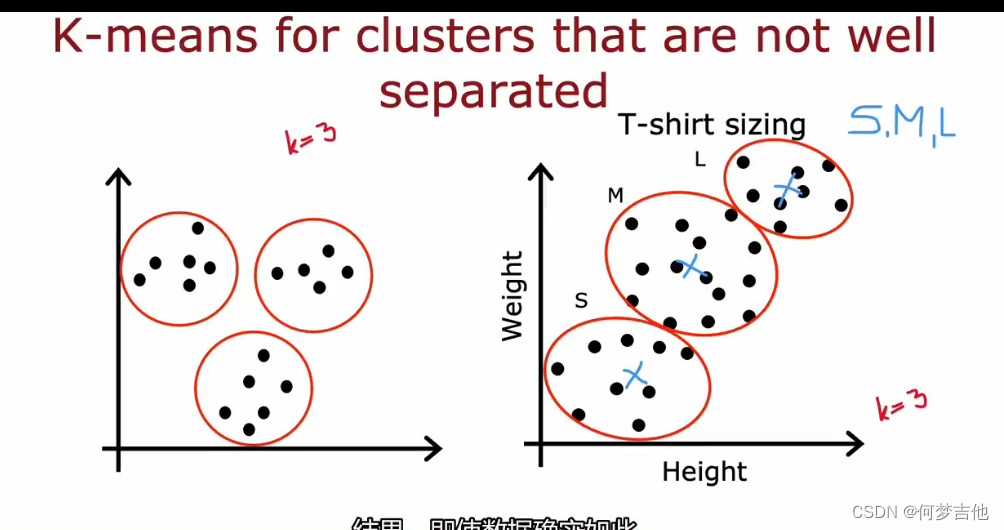
对于不那么好分离的簇，K-means也适用例子：设计师划分短袖的尺码标准SML

10.1.2 K-means的代价函数（失真函数distortion function）

一些符号

Ci，表示当前训练样本Xi所在的簇的索引1~k，是每个样本的分类标识
uk 是簇质心的位置
当k=Ci时，uci是样本Xi被分配到的簇，这个簇的簇质心的位置
m是所有样本个数
在这里插入图片描述
算法每一步会更新样本所属簇的类别即Ci的值、
或者移动簇质心的位置uk，以降低代价函数

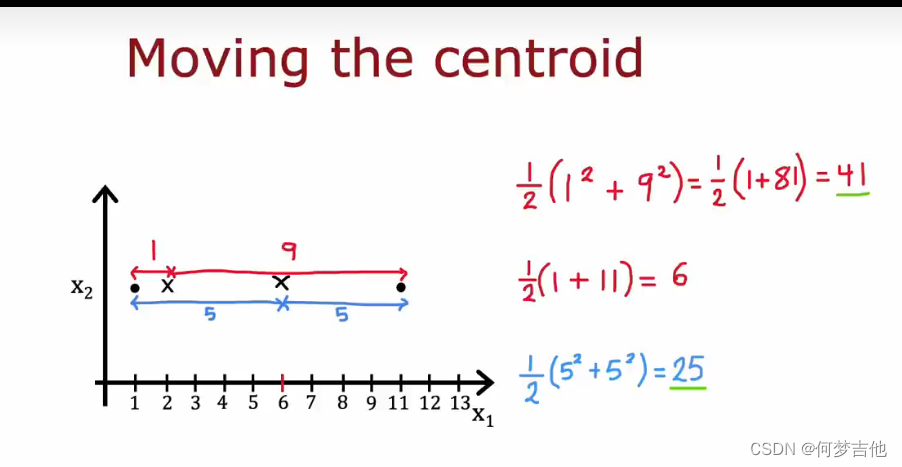
用多个不同的簇质心初始值初始化

10.1.3 初始化K-means

K-means 聚类算法第一步**是为簇质心

       μ 
      
     
       j 
      
     
    
   
     \mu_j 
    
   
 μj 
  
   
    
     
     
       μ 
      
     
       k 
      
     
    
   
     \mu_k 
    
   
 μk 选择随机位置作为初始值**

如果初始值选的不好，会陷入局部最小值，多次运行K-means，计算他们的J，选最小的那个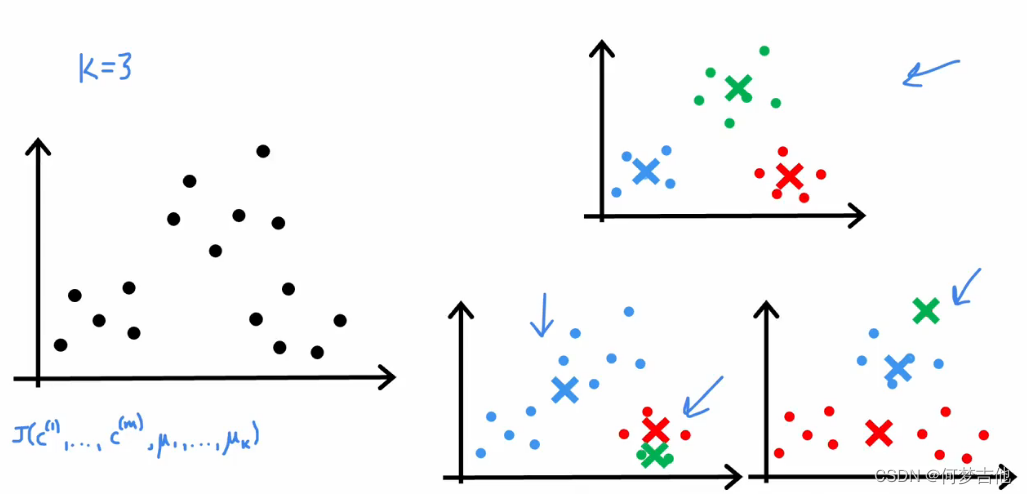
在这里插入图片描述

算法 多次随机初始化

在这里插入图片描述

10.1.3 如何选择聚类的簇的数量K

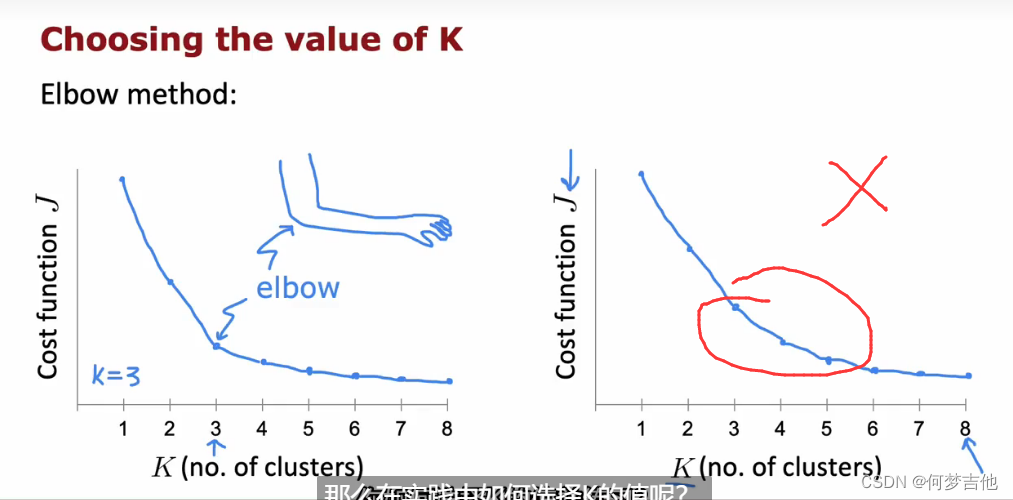
肘部法则 elbow method （一般不用）运行具有各种K值的k-means，绘制代价函数-K的函数，找到肘关节位置，但比较主观
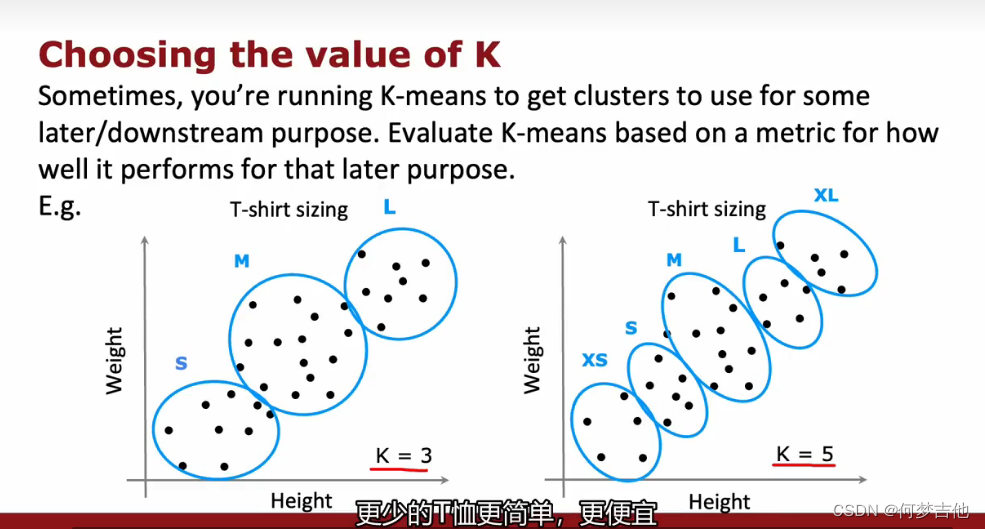
根据K-means在稍后或下游任务中的表现来评估具体的K值合不合适 例子：短袖尺码划分你的业务需求到底需要3个尺码，还是5个尺码？

10.2 异常检测

10.2.1 密度估计density estimation

在这里插入图片描述
异常检测中的密度估计是指根据已知数据集的分布情况，推测新的样本数据在该数据集中的概率分布，并利用这种概率分布来判断样本是否异常。

一种常见的密度估计方法是基于高斯混合模型（Gaussian Mixture Model, GMM）的方法。假设已知数据集由多个高斯分布组成，每个高斯分布对应数据集中的一个簇，那么可以通过最大化似然函数来估计这些高斯分布的参数，从而得到整个数据集的概率分布模型。具体来说，对于一个新的样本数据，可以计算它在该模型下的概率密度值，如果该值较小，则认为该样本是异常值。

10.2.2 高斯正态分布Gaussian （Normal） Distribution

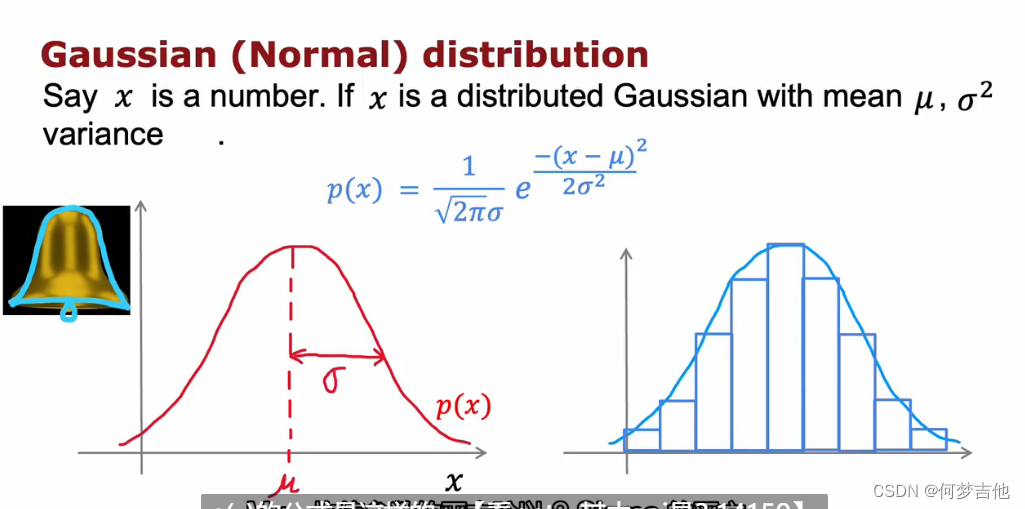
在这里插入图片描述
计算样本的mu 和sigma，得到高斯分布（这里除以m-1和除以m都是可以的！）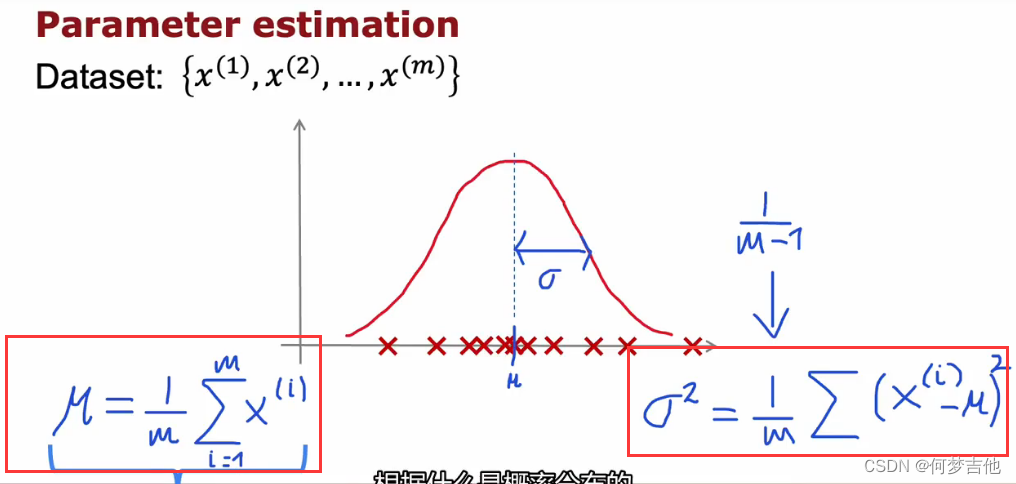

利用3sigma原则判断是否为异常值

在实际应用中，3 sigma原则通常用于质量控制和异常值检测。例如，对于某一批次的生产产品，如果其尺寸的标准差小于三倍，那么可以认为这批产品的尺寸基本上是符合要求的。而如果有个别产品尺寸偏离平均值超过三倍标准差，那么这个产品就可以被认为是异常值，需要进行进一步的检测和处理。

这里x是单个数字，单一特征，对应的异常检测只有一个特征，但实际会有很多特征

10.2.3 异常检测算法

公式符号

每一个样本xi都有n个特征，x是一个特征向量，在这里比如发动机的热量和振动，我们要做的是密度估计，估计p(x)。

这个 特征向量x的所有特征的概率p(x) 是p(x1)*p(x2)…p(xn)，为了给x1的概率建模，比如这个例子中的第一个特征热量，我们有两个参数mu1 、 sigma1（我们需要估计所有样本的所有特征x1的均值和方差）

X(i) 表示的是第几个样本，X（i)j 表示的是第i个样本的第j个特征

加粗样式

算法通过px分布来形象化理解异常检测

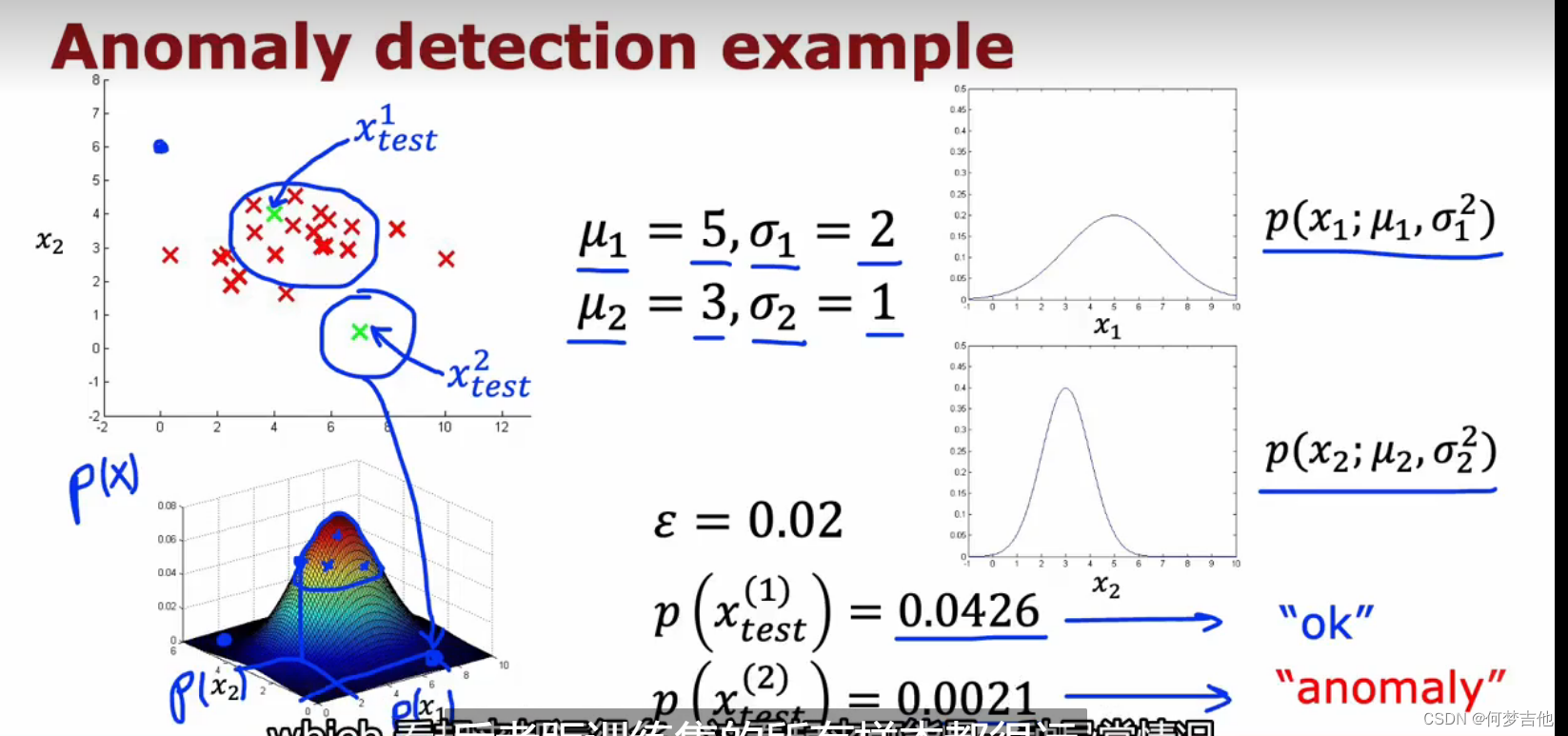
10.2.4 异常检测的一些技巧

强化学习 reinforcement learning

python中科学计数法E

在数学中，矩阵特征值和特征向量是很重要的概念，它们可以帮助我们理解和分析矩阵的性质和行为。其中，特征值是一个标量，表示矩阵沿着某个方向的缩放比例，而特征向量则是一个非零向量，表示在这个方向上的向量不变，只是被缩放了。

在机器学习中，我们通常会对数据进行特征提取和降维，其中一种常见的方法是使用主成分分析（Principal Component Analysis, PCA）。PCA通过对数据进行矩阵分解，将原始数据转化为一组线性无关的主成分，以实现数据降维的目的。

在PCA中，我们需要计算数据的协方差矩阵，并求解其特征值和特征向量。具体地，如果我们有一个

     m 
    
   
  
    m 
   
  
m维数据集 
 
  
   
   
     X 
    
   
  
    X 
   
  
X，其中每个样本都有 
 
  
   
   
     n 
    
   
  
    n 
   
  
n个特征，那么协方差矩阵 
 
  
   
   
     C 
    
   
  
    C 
   
  
C的维度就是 
 
  
   
   
     n 
    
   
     × 
    
   
     n 
    
   
  
    n \times n 
   
  
n×n，可以通过如下公式计算：


  
   
    
    
      C 
     
    
      = 
     
     
     
       1 
      
     
       m 
      
     
    
      ( 
     
    
      X 
     
    
      − 
     
     
     
       X 
      
     
       ˉ 
      
     
     
     
       ) 
      
     
       T 
      
     
    
      ( 
     
    
      X 
     
    
      − 
     
     
     
       X 
      
     
       ˉ 
      
     
    
      ) 
     
    
   
     C = \frac{1}{m}(X-\bar{X})^T(X-\bar{X}) 
    
   
 C=m1(X−Xˉ)T(X−Xˉ)

其中

      X 
     
    
      ˉ 
     
    
   
  
    \bar{X} 
   
  
Xˉ是数据的均值向量，表示每个特征的均值。然后，我们可以通过对协方差矩阵求解特征值和特征向量，将原始数据转化为一组新的主成分。

在实际计算中，我们通常使用特征值分解或奇异值分解（Singular Value Decomposition, SVD）来求解特征值和特征向量。特征向量编码就是将数据转化为特征向量的一种方式，具体来说，可以将数据投影到特征向量所表示的方向上，从而得到一组新的特征值表示。

例如，假设我们有一个

     2 
    
   
     × 
    
   
     2 
    
   
  
    2 \times 2 
   
  
2×2的矩阵 
 
  
   
   
     A 
    
   
  
    A 
   
  
A，其特征值为 
 
  
   
    
    
      λ 
     
    
      1 
     
    
   
     = 
    
   
     3 
    
   
     , 
    
    
    
      λ 
     
    
      2 
     
    
   
     = 
    
   
     1 
    
   
  
    \lambda_1=3,\lambda_2=1 
   
  
λ1=3,λ2=1，特征向量为 
 
  
   
    
    
      v 
     
    
      1 
     
    
   
     = 
    
   
     [ 
    
   
     1 
    
   
     , 
    
   
     2 
    
    
    
      ] 
     
    
      T 
     
    
   
     , 
    
    
    
      v 
     
    
      2 
     
    
   
     = 
    
   
     [ 
    
   
     2 
    
   
     , 
    
   
     − 
    
   
     1 
    
    
    
      ] 
     
    
      T 
     
    
   
  
    v_1=[1,2]^T,v_2=[2,-1]^T 
   
  
v1=[1,2]T,v2=[2,−1]T，那么我们可以将一个列向量 
 
  
   
   
     x 
    
   
     = 
    
   
     [ 
    
    
    
      x 
     
    
      1 
     
    
   
     , 
    
    
    
      x 
     
    
      2 
     
    
    
    
      ] 
     
    
      T 
     
    
   
  
    x=[x_1,x_2]^T 
   
  
x=[x1,x2]T投影到 
 
  
   
    
    
      v 
     
    
      1 
     
    
   
  
    v_1 
   
  
v1和 
 
  
   
    
    
      v 
     
    
      2 
     
    
   
  
    v_2 
   
  
v2所表示的方向上，得到一组新的特征值表示：


  
   
    
     
     
       y 
      
     
       1 
      
     
    
      = 
     
    
      x 
     
    
      ⋅ 
     
     
     
       v 
      
     
       1 
      
     
    
      = 
     
    
      [ 
     
     
     
       x 
      
     
       1 
      
     
    
      , 
     
     
     
       x 
      
     
       2 
      
     
     
     
       ] 
      
     
       T 
      
     
    
      ⋅ 
     
    
      [ 
     
    
      1 
     
    
      , 
     
    
      2 
     
     
     
       ] 
      
     
       T 
      
     
    
      = 
     
     
     
       x 
      
     
       1 
      
     
    
      + 
     
    
      2 
     
     
     
       x 
      
     
       2 
      
     
    
   
     y_1 = x \cdot v_1 = [x_1,x_2]^T \cdot [1,2]^T = x_1+2x_2 
    
   
 y1=x⋅v1=[x1,x2]T⋅[1,2]T=x1+2x2


  
   
    
     
     
       y 
      
     
       2 
      
     
    
      = 
     
    
      x 
     
    
      ⋅ 
     
     
     
       v 
      
     
       2 
      
     
    
      = 
     
    
      [ 
     
     
     
       x 
      
     
       1 
      
     
    
      , 
     
     
     
       x 
      
     
       2 
      
     
     
     
       ] 
      
     
       T 
      
     
    
      ⋅ 
     
    
      [ 
     
    
      2 
     
    
      , 
     
    
      − 
     
    
      1 
     
     
     
       ] 
      
     
       T 
      
     
    
      = 
     
    
      2 
     
     
     
       x 
      
     
       1 
      
     
    
      − 
     
     
     
       x 
      
     
       2 
      
     
    
   
     y_2 = x \cdot v_2 = [x_1,x_2]^T \cdot [2,-1]^T = 2x_1-x_2 
    
   
 y2=x⋅v2=[x1,x2]T⋅[2,−1]T=2x1−x2

其中，

      y 
     
    
      1 
     
    
   
  
    y_1 
   
  
y1和 
 
  
   
    
    
      y 
     
    
      2 
     
    
   
  
    y_2 
   
  
y2就是原始数据在特征向量 
 
  
   
    
    
      v 
     
    
      1 
     
    
   
  
    v_1 
   
  
v1和 
 
  
   
    
    
      v 
     
    
      2 
     
    
   
  
    v_2 
   
  
v2所表示

numpy语法

np.c_ [ , ]用于连接两个矩阵, 可以用来对比数据前后
reshape的用法

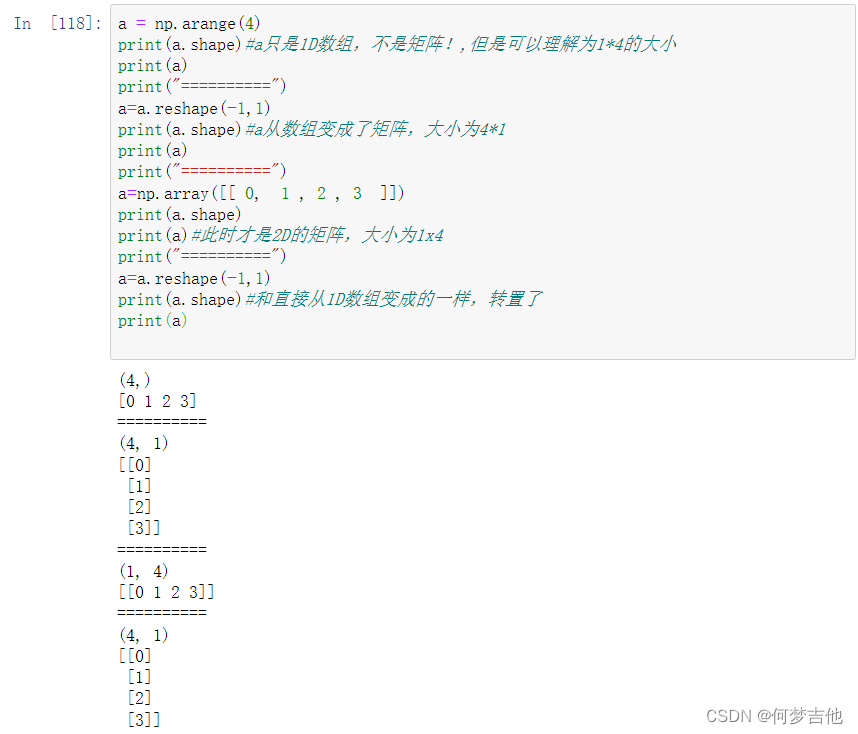
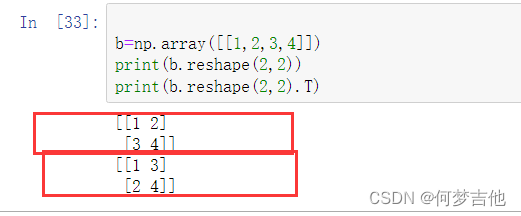
reshape 相当于截断硬凑，需要转置,T

np.exp() e底数
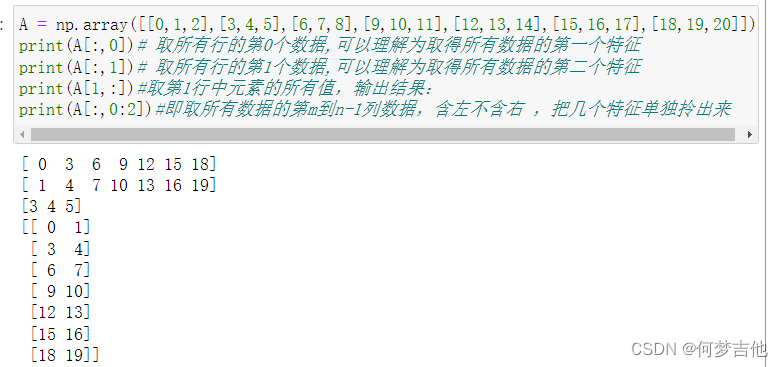
X[:,0]就是拉出矩阵的第1列，
np.zeros和np.zeros_like 设置一个由0组成的数组，后者可以传入一个矩阵
二维以上矩阵乘法np.matmul(A,W) 用 @也可以其中A=np.array([[200,17]]) 是2D数组也就是矩阵这边两个[[!!dot也是矩阵乘法，但只能是二维矩阵 dot其实是向量的点积叉乘运算
矩阵转置的三种方法 1. 二维数组.T2. 高维数组 transpose()、两轴对换swapaxes https://www.jb51.net/article/162035.htm

Scikit-Learn库

LogisticRegression().fit(X, y)  在训练数据上拟合这个模型
y_pred = lr_model.predict(X) 预测
lr_model.score(X, y)) 计算在训练集上的准确率

TensorFlow

数据表示

在TensorFlow内部中用矩阵表示数据 Tensor 张量可以看做表示矩阵的一种方式 [[200,17]] 是2D数组就是矩阵 [200,17] 是1D数组
把tensor 转换成numpy数组

Keras

Tensorflow中并发布了Tensorflow 2.0。Keras是一个由François Chollet独立开发的框架，为Tensorflow创建了一个简单的、以层为中心的接口。

对数据进行归一化 Normalization

print(f"Temperature Max, Min pre normalization: {np.max(X[:,0]):0.2f}, {np.min(X[:,0]):0.2f}")print(f"Duration    Max, Min pre normalization: {np.max(X[:,1]):0.2f}, {np.min(X[:,1]):0.2f}")
norm_l = tf.keras.layers.Normalization(axis=-1)# 
norm_l.adapt(X)# learns mean, variance
Xn = norm_l(X)print(f"Temperature Max, Min post normalization: {np.max(Xn[:,0]):0.2f}, {np.min(Xn[:,0]):0.2f}")print(f"Duration    Max, Min post normalization: {np.max(Xn[:,1]):0.2f}, {np.min(Xn[:,1]):0.2f}")

查看网络的描述 model.summary()
查看某一层的参数，查看参数形状

[layer1, layer2, layer3]= model.layers
W1,b1 = layer1.get_weights()

我们也可以直接以张量的形式访问权重。

model.layers[2].weights

model.compile语句定义了一个损失函数并指定了一个编译优化。

model.compile(
    loss=tf.keras.losses.BinaryCrossentropy(),
    optimizer=tf.keras.optimizers.Adam(0.001),)

model.fit语句运行梯度下降，并将权重与数据拟合。


model.fit(
    X,y,
    epochs=20)

预测model.predict 预测的输入是一个数组，所以单个例子被重塑为二维的。

Python常用技巧

格式打印 f字符串

print(f"Iteration {i:4}: Cost {float(J_history[-1]):8.2f}   ")#8.2f代表左对齐8格,保留小数点后两位 为float浮点型

加载数据集

load_data("data/ex2data1.txt")

利用bool 索引分别画图(把0 1情况的数据分离开 )

X_train = np.array([0.,1,2,3,4,5], dtype=np.float32).reshape(-1,1)# 2-D Matrix
Y_train = np.array([0,0,0,1,1,1], dtype=np.float32).reshape(-1,1)# 2-D Matrix

pos = Y_train ==1#positive->注意：本处采用的是bool索引
neg = Y_train ==0#negeative
X_train[pos]#array([3., 4., 5.], dtype=float32)

fig,ax = plt.subplots(1,1,figsize=(4,3))
ax.scatter(X_train[pos], Y_train[pos], marker='x', s=80, c ='red', label="y=1")
ax.scatter(X_train[neg], Y_train[neg], marker='o', s=100, label="y=0", facecolors='none', 
              edgecolors=dlc["dlblue"],lw=3)

ax.set_ylim(-0.08,1.1)
ax.set_ylabel('y', fontsize=12)
ax.set_xlabel('x', fontsize=12)
ax.set_title('one variable plot')
ax.legend(fontsize=12)
plt.show()

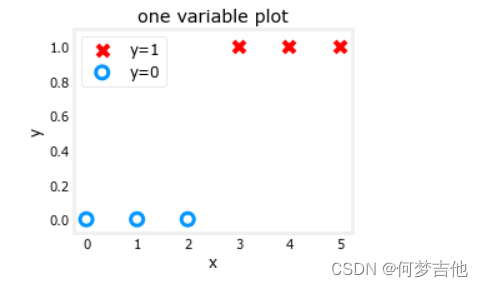
在这里插入图片描述

类型转换

.astype(int)

英文积累

with respect to 关于
omit 省略
make inroad 进军
illustrate 展示
Toggle 切换
one half 1/2
formidable-looking 看起来相当可怕的
property 特性
get stucked 被卡住
incorporates 包含住
summation 求和 cigema
mintage 年份
to recap 回顾一下
heuristic 启发式的
plateaus 高原
peek to peek 峰间值
Out of the box 开箱即用
penalize 惩罚
mapped against 映射
concatenate 连接
scenario 局面
training example 训练示例
derivative 导数 derivation 推导
1 over m m分之一
sum of i equals 1 through m i从1到m的总和
calculus 微积分
convergence 收敛 diverge. 发散
local minimum 局部最小值 global
convex function 凸函数，碗型，一个局部最小值
intuitive name 直观的名称
subset 子集
automate 使自动化
plotting routines 绘图例程、程序
Convention 惯例
embedded comments 嵌入的注释
quiver plot 箭头图查看两个参数的梯度的方法
magnitude 大小幅度规模
scaled 比例的 scale 尺度、缩放 scale well to 适用于可用于
primarily for 主要用于
A versus B A 与B的关系
measure of 衡量
in line with 符合一致
a contour plot 等高线图
steady (monotonic) progress 稳步（单调）前进
Zooming in, 放大
oscillates from positive to negative 在正数和符数之间摆动
delve into 研读
subscript sub 下标 superscript 上标
parentheses 括号
algebra 代数 linear algebra 线性代数
dot products 点积 the product of 积
numerical linear algebra library 数值线性代数库 numpy
vertorization 矢量化
square bracket 方括号 [ ]
period 句点 dot 点 comma 逗号
fairly seamlessly 相当完美无缝的
specify the shape 指定形状
a mainstay of 主要内容，中流砥柱 main stay
aligning 对齐
back-end 后端的
display precision 显示精度
notionally 在概念上
1-D 一维的
roughly 大致的
Going forward 往后
scatter plot 散点图
standard deviation 标准差 deviation 偏差
normal distribution 正态分布
as a rule of thumb 根据经验
aim for about -1 争取约为 -1
flatten out 拉平了变平了
trade-of 权衡
threefold 3 倍
overshooting 过头了
oscillating 摆动震荡
magnitude 大小
lot 地段一小块土地 loft 公寓
a quadratic function 二次函数 cubic function 三次函数
practitioner 从业者
all but 几乎差不多
interchangebly 互换的
normalize 归一化
intercept 截距
coefficient 系数
a close form 接近
semicolon 分号；
a neuron 一个神经元 dendrites 树突 axon 轴突
activation 激活 activations 激活项可数
caveat 警告告诫
vastly 巨大的
awareness 知名度
terminology 术语
corresponding to 分别对应
architecture of the neural network 神经网络的架构
multilayer perceptron 多层感知器（有多层的神经网络）
rewind the video 倒带视频
instantiated 实例化
Sequential 顺序的
the mean and variance of the data set 数据集的均值和方差
be accounted for 被计算、考虑在内
interpret 解释
replicate 复制
transpose 转置

标签：算法人工智能

本文转载自: https://blog.csdn.net/weixin_45837404/article/details/128709041
版权归原作者 师大阿林 所有，如有侵权，请联系我们删除。

【机器学习 吴恩达】2022课程笔记（持续更新）

一、机器学习

1.1 机器学习定义

1.2 监督学习 supervised learning

1.2.1 监督学习定义

1.3 无监督学习 unsupervised learning

1.3.1 无监督学习定义

1.3.2 聚类算法

二、单变量的线性回归 univariate linear regression——预测问题

2.1 单变量线性函数

2.2 梯度下降算法 Gradient Descent algorithm

2.3 用于线性回归的梯度下降 ——Batch梯度下降

三、numpy的向量Vectors、矩阵Matrices

四、多元线性回归 multiple linear regression

4.1多变量线性回归函数

4.2 多元梯度下降法 Gradient Descent With Multiple Variables

4.3 特征缩放 feature scaling (使具有相似的范围)

4.3.1 Mean normalization 均值归一化

4.3.2 Z-score normalization Z-score归一化

4.4 如何选择学习率

4.4.1 学习曲线 learning curve

4.4.2 学习率的选择

4.5 特征和多项式回归polynomial regression

4.5.1 特征工程 feature engineering

4.5.2 多项式回归

五、逻辑回归logistic regression——分类问题

5.1 线性回归对于分类问题的局限性

5.2 决策边界 decision boundary

5.3 代价函数 cost function

5.3.1 cost function的导出

5.3.2 逻辑回归的损失函数

5.3.3 简化代价函数 与 梯度下降

六、 过拟合问题

6.1 过拟合定义

6.2 过拟合的代价函数（正则化原理）

6.3 用于线性回归的正则方法 Regularized Linear Regression

6.4 用于线性回归的正则方法 Regularized Linear Regression

七、神经网络(深度学习算法)

7.1 认识神经网络

7.2 如何在神经网络上推理

7.2.1 神经网络的定义

7.2.2 构建：前向传播 forward propagation （使用TensorFlow实现）

7.2.3 矢量化（让神经网络运行更快）

7.2.4 矩阵乘法

7.2.5 C2_W1_Assignment 01识别

7.4 训练神经网络

7.4.1 模型训练细节

7.4.2 如何选择激活函数

7.5 多分类问题

7.5.1 softmax 回归算法

7.5.2 softmax 改进实现，更加精确

7.5.3 多标签分类问题

7.6 高级优化方法

7.6.1 Adam 算法 自适应距估计 ——自动调节学习率大小

7.7 其他网络层的类型

八、细节

8.1 使用测试集评估模型性能

8.2 模型选择 \ 交叉验证集

8.3 偏差 方差 bias variance

8.4 正则化参数

8.5 指定一个用于性能评估的基准 baseline =》判断是否有高偏差、高方差的情况

8.6 通过学习曲线=》判断是否有高偏差、高方差

8.7 误差分析

8.8 添加更多数据的技巧

数据增强

数据合成

8.9 迁移学习 transfer learning（监督预训练）

8.10倾斜数据集的误差指标 Error metrics for skewed datasets

8.10.1 精确率和召回率 Precision/ recall 、混淆矩阵

8.10.2 精确率（找的对）和召回率（找的全）的权衡、F1score

8.11 机器学习项目完整的周期

九、决策树

9.1 衡量纯度、熵entropy、 Gini指数

9.2 信息增益

9.3 独热编码One-hot

9.4 连续值特征

9.5 回归树 regression tree

9.6 树集合 Tree ensemble

9.6.1 有放回抽样sampling with replacement （构造多个随机的训练集）

9.6.2随机森林算法

【机器学习吴恩达】2022课程笔记（持续更新）

5.3.3 简化代价函数与梯度下降

六、过拟合问题

7.6.1 Adam 算法自适应距估计 ——自动调节学习率大小

8.3 偏差方差 bias variance

“【机器学习吴恩达】2022课程笔记（持续更新）”的评论: