决策树专题_以python为工具【Python机器学习系列（十一）】
文章目录
ʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞ
ʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞ
大家好，我是侯小啾！
今天分享的内容是，决策树的原理及其python实现。做决策树之前，往往需要首先选择特征选择的指标，常用的指标有信息增益、信息增益比、基尼系数等。常用的决策树算法有ID3、C4.5、CART算法等，其中，ID3算法使用 信息增益 缺陷是，倾向于分类较多的特征；C4.5算法使用信息增益率；CART算法使用基尼系数。下面先对这些指标进行说明，然后展示决策树代码。
1.关于信息熵的理解
在信息论中，使用 熵 (Entropy)来描述随机变量分布的不确定性。
假设对随机变量X，其可能的取值有
x
1
,
x
2
,
.
.
.
,
x
n
x_1,x_2,...,x_n
x1,x2,...,xn。即有n种可能发生的结果。其对应发生的概率依次为
p
1
,
p
2
,
.
.
.
,
p
n
p_1,p_2,...,p_n
p1,p2,...,pn，则事件
p
i
p_i
pi对应的信息熵为:
H
(
X
)
=
H
(
p
)
=
∑
i
=
1
n
p
i
log
1
p
i
=
−
p
i
log
p
i
H(X)=H(p)=\sum_{i=1}^np_i\log \frac{1}{p_i}=-p_i\log p_i
H(X)=H(p)=∑i=1npilogpi1=−pilogpi
信息熵中log的底数通常为2，理论上可以使用不同的底数。
如何理解信息熵呢，假设已知今天是周日，则对于“明天是周几”这件事，只有一种可能的结果：是周一，且p=1。则“明天是周几”的信息熵
H
(
X
)
H(X)
H(X)为
−
1
×
log
1
=
0
-1×\log 1=0
−1×log1=0，取信息熵的最小值0。表示“明天是周几”这个话题的不确定性很低，明天周几很确定。
再比如抛一枚硬币，则结果为正面和反面的概率都是0.5。则信息熵为
l
o
g
2
log2
log2，相比“明天周几”这件事的信息熵稍大些了。
假设某事情有100中可能的结果，每种结果发生的概率为0.01。则
H
(
X
)
=
l
o
g
100
H(X)=log100
H(X)=log100，对于等概率均匀分布的事件，不确定的结果种类越多，则熵越大。
2.信息增益
什么是信息增益？可以通过这个示例来理解。
假设给定某连续7天样本数据，在这七天内，张三在工作日（周一至周五）中有两天打了篮球，在周六周日两天中有一天打了篮球。则我们可以得出：张三在任意一天打篮球的概率为
3
7
\frac{3}{7}
73，张三在工作日打篮球的概率为
2
5
\frac{2}{5}
52，张三在周六、周日打篮球的概率为
1
2
\frac{1}{2}
21。
张三打篮球的信息熵为
H
(
X
)
=
−
3
7
log
3
7
−
4
7
log
4
7
H(X)=-\frac{3}{7}\log\frac{3}{7}-\frac{4}{7}\log\frac{4}{7}
H(X)=−73log73−74log74
张三在工作日打篮球的信息熵为
H
(
X
∣
A
1
)
=
−
2
5
log
2
5
−
3
5
log
3
5
H(X|A_1)=-\frac{2}{5}\log\frac{2}{5}-\frac{3}{5}\log\frac{3}{5}
H(X∣A1)=−52log52−53log53
张三在非工作日打篮球的信息熵为
H
(
X
∣
A
2
)
=
−
1
2
log
1
2
−
1
2
log
1
2
=
log
2
H(X|A_2)=-\frac{1}{2}\log\frac{1}{2}-\frac{1}{2}\log\frac{1}{2}=\log2
H(X∣A2)=−21log21−21log21=log2
则张三在工作日打篮球的信息增益为 张三打篮球的信息熵 减去 张三在工作日打篮球的信息熵，即
H
(
X
)
−
H
(
X
∣
A
1
)
H(X)-H(X|A_1)
H(X)−H(X∣A1)
张三在非工作日打篮球的信息增益为 张三打篮球的信息熵 减去 张三在非工作日打篮球的信息熵。
H
(
X
)
−
H
(
X
∣
A
2
)
H(X)-H(X|A_2)
H(X)−H(X∣A2)
信息增益的公式可以表述为：
H
(
X
)
−
H
(
X
∣
A
i
)
H(X)-H(X|A_i)
H(X)−H(X∣Ai)
看到这里，大概可以明白，信息增益，即在衡量某事件
A
i
A_i
Ai的发生对目标话题的不确定性的降低程度。
3.信息增益比
信息增益比是对不确定性降低程度的另一种衡量方式，即以比值的形式来呈现，其在计算出信息增益的基础上，再使用信息增益除以 在事件
A
i
A_i
Ai发生情况下的信息熵，即为信息增益比，公式表示为
H
(
X
)
−
H
(
X
∣
A
i
)
H
(
X
∣
A
i
)
\frac{H(X)-H(X|A_i)}{H(X|A_i)}
H(X∣Ai)H(X)−H(X∣Ai)
这里不再使用示例进行说明。
4.基尼指数
基尼指数的公式为：
G
i
n
i
(
X
)
=
1
−
∑
i
=
1
k
p
i
2
Gini(X)=1-\sum_{i=1}^kp_i^2
Gini(X)=1−∑i=1kpi2
基尼指数用来反应样本集合的纯度（或者说是“不纯度”），当所有样本都只属于一个类别时，基尼指数值为0，纯度最高（不纯度最小）。基尼指数越大，则纯度越低（不纯度越大）。
依然可以假设给定某连续7天样本数据，在这七天内，张三在工作日（周一至周五）中有两天打了篮球，在周六周日两天中有一天打了篮球。则事件“任意一天张三是否打篮球”的基尼系数为
1
−
(
3
7
)
2
−
(
4
7
)
2
1-(\frac{3}{7})^2-(\frac{4}{7})^2
1−(73)2−(74)2。
“张三在工作日是否打篮球”的基尼指数，为
g
i
n
i
1
=
1
−
(
2
5
)
2
−
(
3
5
)
2
gini_1=1-(\frac{2}{5})^2-(\frac{3}{5})^2
gini1=1−(52)2−(53)2
“张三在非工作日是否打篮球”的基尼指数，为
g
i
n
i
2
=
1
−
(
1
2
)
2
−
(
1
2
)
2
gini_2=1-(\frac{1}{2})^2-(\frac{1}{2})^2
gini2=1−(21)2−(21)2
则“张三今天是否打篮球”关于“今天是否是工作日”的基尼系数为
5
7
×
g
i
n
i
1
+
2
7
×
g
i
n
i
2
\frac{5}{7}×gini_1 + \frac{2}{7}×gini_2
75×gini1+72×gini2，这里的计算方式是将上边两个基尼指数加权求和。
相应的，基尼指数不能直接作为特征选择指标，可以使用基尼指数增益。公式类比信息增益与信息熵即可。
5.DecisionTreeClassifier()与DecisionTreeRegressor()
python的sklearn库创建决策树的方法为**DecisionTreeClassifier()和DecisionTreeRegressor()**。其中DecisionTreeClassifier()用于解决分类问题，而DecisionTreeRegressor()用于解决回归问题。
实例化这两个类以创建决策树模型时，默认为使用CART算法，即参数criterion默认为"gini"，特征选择为基尼系数。
当criterion为"entropy"时表示ID3算法，表示使用信息增益构建决策树。
目前只有这两种，python的sklearn库没有提供关于信息增益比的参数，即 C4.5算法。
6.决策树分类 - 葡萄酒分类_DecisionTreeClassifier
使用DecisionTreeClassifier()创建决策树分类模型，对标签为离散类别的数据进行分类，代码及效果如下：
from sklearn.datasets import load_wine
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
wine = load_wine()
x_data = wine.data
y_data = wine.target
x_train, x_test, y_train, y_test = train_test_split(x_data, y_data)# 特征选择指标为 信息增益
clf = DecisionTreeClassifier(criterion="entropy")# 训练模型
clf.fit(x_train, y_train)# 预测
predict_result = clf.predict(x_test)print(predict_result)
预测结果如下：
绘制决策树。
可以通过以下代码将决策树更直观地展示出来：
import graphviz
from sklearn import tree
dot_data = tree.export_graphviz(
clf,
filled=True,
rounded=True,
special_characters=True)# 将dot数据进行可视化
graph = graphviz.Source(dot_data)# 将决策树渲染到pdf文件中
graph.render("wine")
代码执行后生成了两个名为“wine”的文件如下图所示：
右边的pdf文件即为我们得到的决策树图像。如下图所示：
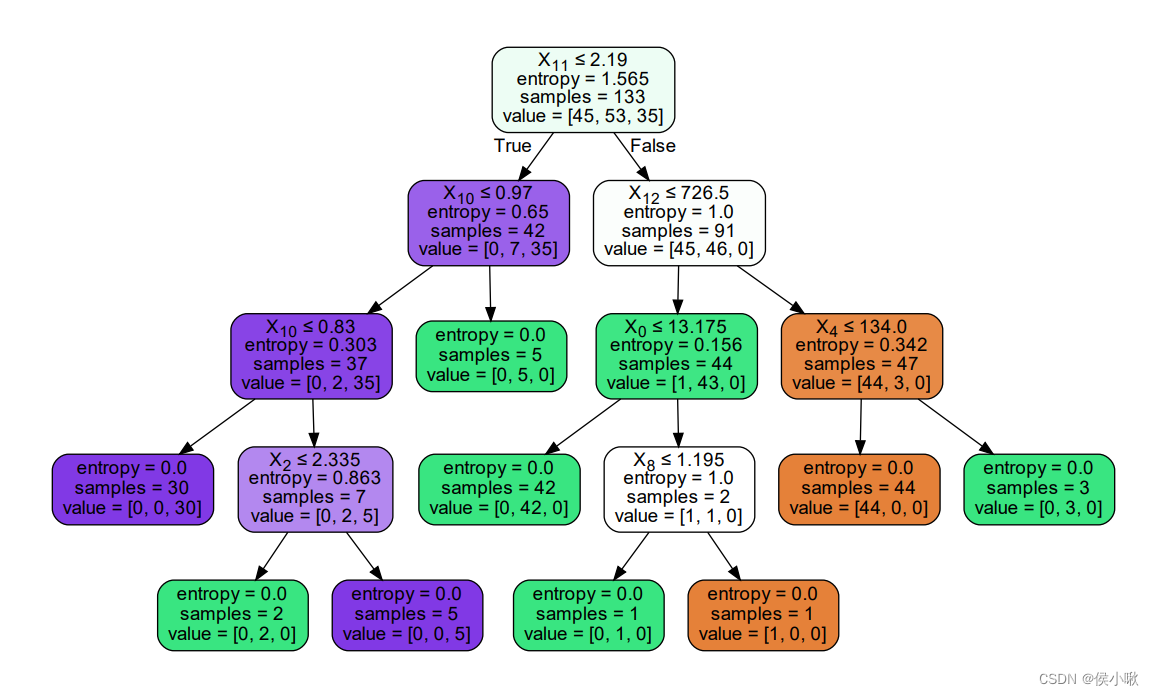
如何理解这张图呢？
葡萄酒分类数据集中，训练集数据共有133个，共有13个特征可供做决策（即
x
1
x_1
x1到
x
13
x_{13}
x13），标签共有三类（0,1，2）。从图形的顶端往下看，顶端第一个决策条件为
x
11
≤
2.19
x_{11}≤2.19
x11≤2.19，在这里将进行第一次判断，此处的信息熵值为13565，为该图形中最大的信息熵，即该处不确定性最大。从这里往下，可以看到，信息熵的值在不断减小。如果第一次判断为True，则下一次的判断标准为
x
10
x_{10}
x10是否小于等于0.97，是则继续向左分叉，否则向右分叉；如果第一次判断为False，则下一次判断的标准为
x
12
x_{12}
x12是否小于等于726.5。如此往复。
可以看到图像中的条件框共有五种颜色，而我们需要关注的是末端节点的颜色。末端节点的颜色共有三种，深紫色，绿色和橘黄色，对应标签的三种类别。而浅紫色和白色的出现只是视觉效果过程需要，而不再我们关注范围内。
当数据过于复杂导致决策树过于复杂庞大时，请谨慎绘制，pdf文件可能会难以输出。或者建议进行剪枝以降低决策树复杂度。
7.决策树回归 -加利福尼亚房价_DecisionTreeRegressor
以加利福尼亚房价数据集为例，该数据集的标签为连续的数据，而非上例中那种离散的类别。所以使用DecisionTreeRegressor()类创建决策树。使用默认的CART算法实现决策树（即选择基尼指数为特征选择指标），代码如下：
from sklearn.datasets import load_boston
from sklearn.tree import DecisionTreeRegressor
from sklearn.model_selection import train_test_split
from sklearn.datasets import fetch_california_housing
# 加载加利福尼亚房价数据
housing = fetch_california_housing()
features = housing.data
price = housing.target
# 进行数据分割
train_feature, test_feature, train_price, test_price = train_test_split(features, price, test_size=0.3)# 创建决策树 默认参数criterion='gini'，默认CART算法，特征选择指标为基尼指数。
dtr = DecisionTreeRegressor()# 训练
dtr.fit(train_feature, train_price)# 预测
predict_price = dtr.predict(test_feature)print(predict_price)
预测结果如下图所示：
本次分享就到这里，小啾感谢您的关注与支持！
🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ
本专栏更多好文欢迎点击下方连接：
1.初识机器学习前导内容_你需要知道的基本概念罗列_以PY为工具 【Python机器学习系列（一）】
2.sklearn库数据标准预处理合集_【Python机器学习系列（二）】
3.K_近邻算法_分类Ionosphere电离层数据【python机器学习系列（三）】
4.python机器学习 一元线性回归 梯度下降法的实现 【Python机器学习系列（四）】
5.sklearn实现一元线性回归 【Python机器学习系列（五）】
6.多元线性回归_梯度下降法实现【Python机器学习系列（六）】
7.sklearn实现多元线性回归 【Python机器学习系列（七）】
8.sklearn实现多项式线性回归_一元/多元 【Python机器学习系列（八）】
9.逻辑回归原理梳理_以python为工具 【Python机器学习系列（九）】
10.sklearn实现逻辑回归_以python为工具【Python机器学习系列（十）】
版权归原作者 侯小啾 所有， 如有侵权，请联系我们删除。