对于任何一门语言,单词在句子中的位置以及排列顺序是非常重要的,它们不仅是一个句子的语法结构的组成部分,更是表达语义的重要概念。一个单词在句子的位置或排列顺序不同,可能整个句子的意思就发生了偏差。举个例子来说:
I do not like the story of the movie, but I do like the cast.
I do like the story of the movie, but I do not like the cast.
上面这两句话所使用的的单词完全一样,但是所表达的句意却截然相反。那么,引入词序信息有助于区别这两句话的意思。
什么是位置编码
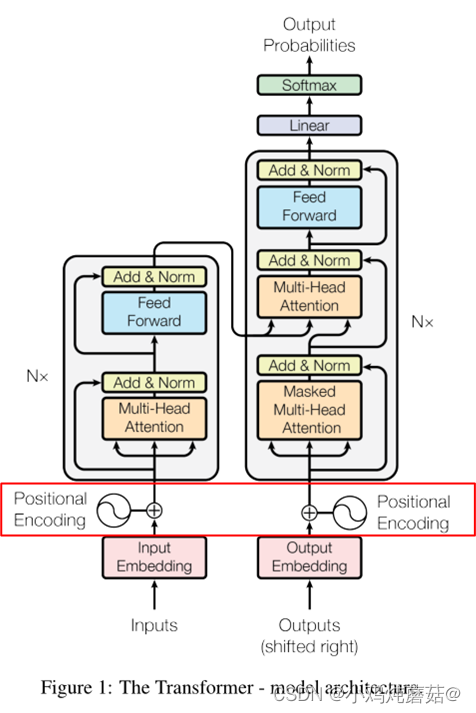
在transformer的encoder和decoder的输入层中,使用了Positional Encoding,使得最终的输入满足:
input = input_embedding + positional_embedding
在transformer模型中,输入的是一排排的句子,对于人类来说可以很容易的看出句子中每个单词的顺序,即位置信息,例如:
(1)绝对位置信息。a1是第一个token,a2是第二个token......
(2)相对位置信息。a2在a1的后面一位,a4在a2的后面两位......
(3)不同位置间的距离。a1和a3差两个位置,a1和a4差三个位置....
但是这对于机器来说却是一件很困难的事情,transformer中的self-attention能够学习到句子中每个单词之间的相关性,关注其中重要的信息,但是却无法学习到每个单词的位置信息,所以说我们需要在模型中另外添加token的位置信息。
Transformer模型抛弃了RNN、CNN作为序列学习的基本模型。我们知道,循环神经网络本身就是一种顺序结构,天生就包含了词在序列中的位置信息。当抛弃循环神经网络结构,完全采用Attention取而代之,这些词序信息就会丢失,模型就没有办法知道每个词在句子中的相对和绝对的位置信息。因此,有必要把词序信号加到词向量上帮助模型学习这些信息,位置编码(Positional Encoding)就是用来解决这种问题的方法。
位置编码(Positional Encoding)是一种用词的位置信息对序列中的每个词进行二次表示的方法,让输入数据携带位置信息,是模型能够找出位置特点。正如前文所述,Transformer模型本身不具备像RNN那样的学习词序信息的能力,需要主动将词序信息喂给模型。那么,模型原先的输入是不含词序信息的词向量,位置编码需要将词序信息和词向量结合起来形成一种新的表示输入给模型,这样模型就具备了学习词序信息的能力。
位置编码的计算
在transformer文章中,位置编码采用的是正余弦编码:

其中,PE表示位置编码,指当前字符在句子中的位置(如:“你好啊”,这句话里面“你”的
),
指的是word embedding的长度(比如说:查表得到“民主”这个词的word embedding为
,则
),
的取值范围是:
。当
的值为偶数是使用上面那条公式,当
的值为奇数时使用下面那条公式。
从图像的角度理解,可以认为pos代表图像的行,i代表当前行对应的列,这样就可以对图像中的每一个像素点进行编码了。
选用三角函数作为位置编码计算公示的原因
在说明为何选取三角函数的形式来计算Positional Encoding之前,不妨先来选取一个简单的Positional Encoding表达方法。给定一个长为的文本,最简单的位置编码就是计数,即使用
作为文本中每个字的位置编码(例如第2个字的Positional Encoding=[1,1,...,1])。但是这种编码有两个缺点:1. 如果一个句子的字数较多,则后面的字比第一个字的Positional Encoding大太多,和word embedding合并以后难免会出现特征在数值上的倾斜;2. 这种位置编码的数值比一般的word embedding的数值要大,对模型可能有一定的干扰。
为了解决上述问题,加入归一化操作,最简单的操作就是将所有值同时初以一个常数T,就像这样:(例如第2个字的Positional Encoding=[1/T,1/T,...,1/T])。这样固然使得所有位置编码都落入
区间,但是问题也是显著的:不同长度文本的位置编码步长是不同的,在较短的文本中紧紧相邻的两个字的位置编码差异,会和长文本中相邻数个字的两个字的位置编码差异一致,如下图所示。

从上图中可以看到第一句的第2个字pos=0.5,第二句中的第5个字pos=0.5,虽然两者的pos值是一样的,但是很明显两者之间位置差异是很大的。
由于上面两种方法都行不通,于是谷歌的科学家们就想到了另外一种方法——使用三角函数。
优点是:
1、可以使PE分布在区间。
2、不同语句相同位置的字符PE值一样(如:当pos=0时,PE=0)。
缺点是:
三角函数具有周期性,可能出现pos值不同但是PE值相同的情况。
于是我们可以在原始PE的基础上再增加一个维度:,虽然还是可能出现pos值不同但是PE值相同的情况,但是整个PE的周期是不是明显变长了。那如果我们把PE的长度加长到和word embedding一样长呢?就像
,PE的周期就可以看成是无限长的了,换句话说不论pos有多大都不会出现PE值相同的情况。然后谷歌的科学家们为了让PE值的周期更长,还交替使用sin/cos来计算PE的值,于是就得到了开头的那个计算公式:
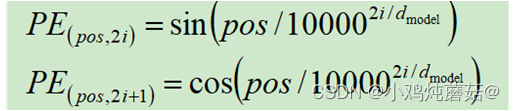
参考文献
Transformer学习笔记一:Positional Encoding(位置编码)
一文读懂Transformer模型的位置编码
Transformer论文解读一(Transformer)
版权归原作者 小鸡炖蘑菇@ 所有, 如有侵权,请联系我们删除。