平衡二叉树详解

一、平衡二叉树

平衡二叉搜索树又被称为AVL树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用实现方法有红黑树、AVL等。

二、作用

我们有时在编程过程中可能会需要用到链表（时间复杂度O(n)）来进行对数据的存储，但是当数据量变得十分庞大时我们对于指定数据的一些操作的时间消耗就会变得大，这时我们就需要借助将链表的结构变为二叉搜索树（时间复杂度O(logn)）来进行数据的存储。
但在某些情况下，例如：对[1,2,3,4,5,6,…]这种其中含有大量有序部分的数组构造二叉搜索树，这会使二叉搜索树类似于链表，这会使对于数据的一些操作的时间复杂度增大到O(n)。
所以一般的二叉搜索树在进行数据的存储时可能会使工作的时间复杂度并未降低太多，这时便需要我们将二叉树的高度尽可能的降低，使二叉树的高度降低为log(n)，这样我们就得到了一个高度平衡的二叉搜索树，使对于数据的一系列操作的时间复杂度稳定在O(logn)。

三、构造平衡二叉树

1、递归

我们可以将需要被构造的数组排序，然后不断从数组的中心递归来构造二叉树。
（参考 力扣1382.将二叉搜索树变平衡）

classSolution{public:
    vector<int> inorderSeq;//将二叉搜索树中的数据通过中序遍历变为有序数组voidgetInorder(TreeNode* o){if(o->left){getInorder(o->left);}
        inorderSeq.push_back(o->val);if(o->right){getInorder(o->right);}}//优先构建数组中心的结点
    TreeNode*build(int l,int r){int mid =(l + r)>>1;//中心位置
        TreeNode* o =newTreeNode(inorderSeq[mid]);if(l <= mid -1){
            o->left =build(l, mid -1);//构建中心结点的左子树}if(mid +1<= r){
            o->right =build(mid +1, r);//构建中心节点的右子树}return o;}

    TreeNode*balanceBST(TreeNode* root){getInorder(root);returnbuild(0, inorderSeq.size()-1);}};

以上方法逻辑简单，但作用于二叉搜索树，其数据本身具有有序性，若对于一组无序的数据，这种方法显然行不通的。
那么我们需要另一种方法来满足一边构造结点，一边检查树是否平衡，一边对数的结构进行优化。

2、旋转

右旋转：

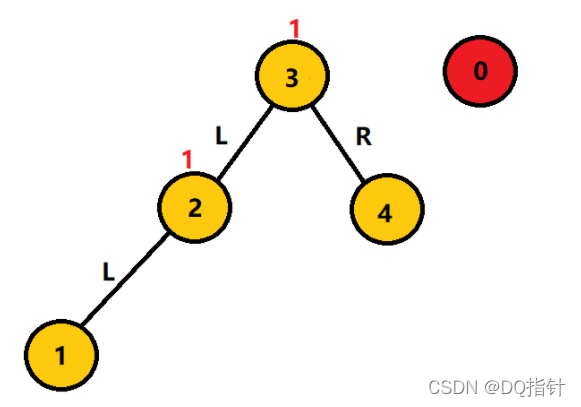
如图，对于一个二叉树的结点我们用其左子树的高度减去其右子树的高度并标记在结点之上，我们这里将其称为高度因子。例如3结点的左子树的高度为2，右子树的高度为1，所以我们将数字1标记在3结点上方。
我们要在此平衡二叉搜索树中插入结点0。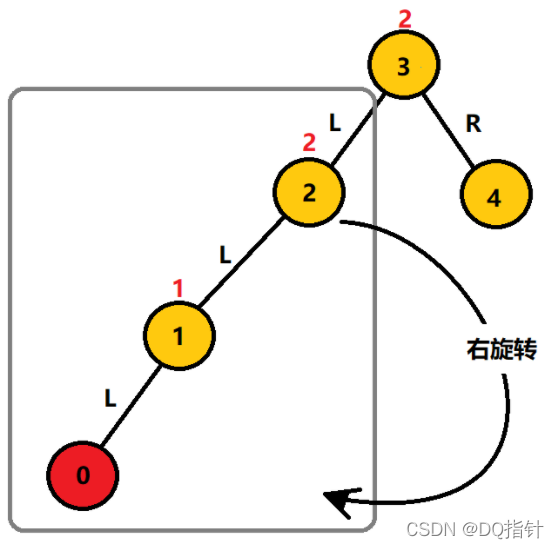

如图，插入0结点后二叉树的平衡被破坏，以结点3和以结点2为根节点的二叉树的高度因子都变为2，显然当高度因子的绝对值大于1时，以该结点为根节点的二叉树是不平衡的，对于这种情况我们只需要把二叉树中高度最小的不平衡子树进行旋转操作，使其高度减一，这样该结点的所有祖先结点的高度因子全部减一，使所有的结点的高度因子的绝对值都不超过1，使二叉树达到平衡。
对于图中的情况，我们只需要对以2结点为根节点的子树进行旋转即可。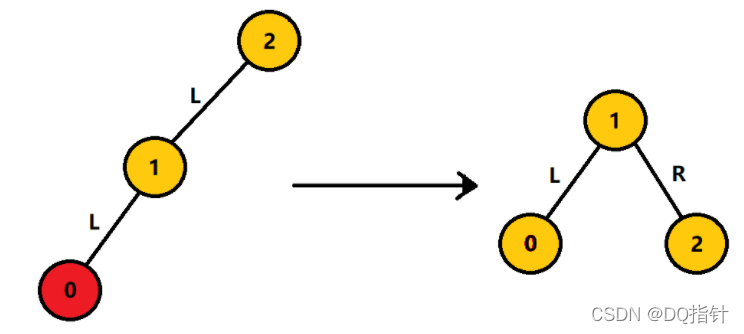

这种出现连续左子树的不平衡的二叉树我们成称LL型，在代码中可以通过高度因子的正负来判断不平衡最小二叉树的类型，需要将该二叉树像图中一样旋转，称为右旋转。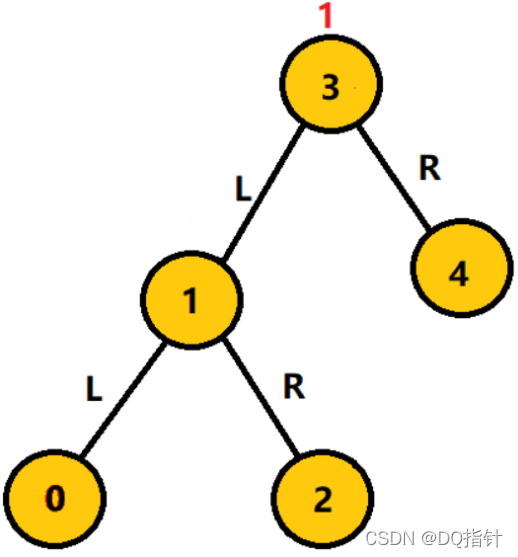

经过旋转之后二叉树的3结点的左子树变为1,1的右子树变为2。
二叉树恢复平衡。

LL旋转（右旋转）伪代码：

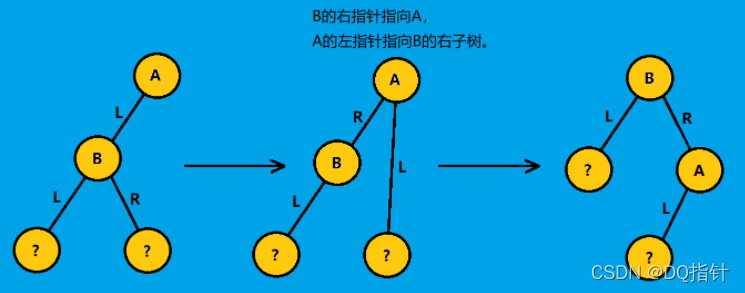
//A为最低不平衡结点，B为A的左节点
AVLTree*RightRotation(Node *A){/* 注意：A必须有一个左子结点B *//* 将A与B做右单旋，更新A与B的高度，返回新的根结点B */
    Node *B = A->Left;
    A->Left = B->Right;
    B->Right = A;
    A->Height =max(GetHeight(A->Left),GetHeight(A->Right))+1;//A更新高度
    B->Height =max(GetHeight(B->Left), A->Height)+1;//B更新高度return B;//返回新的子树根节点，与父亲结点连接}

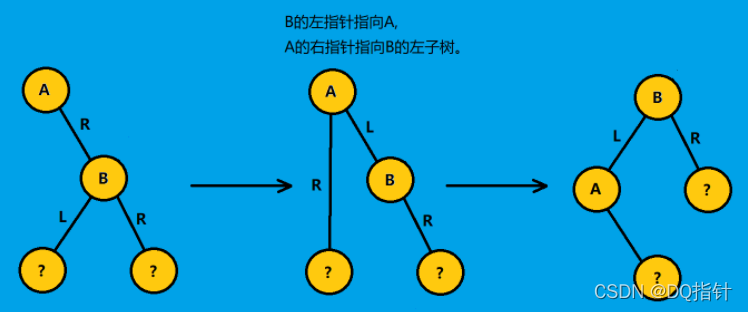
左旋转：

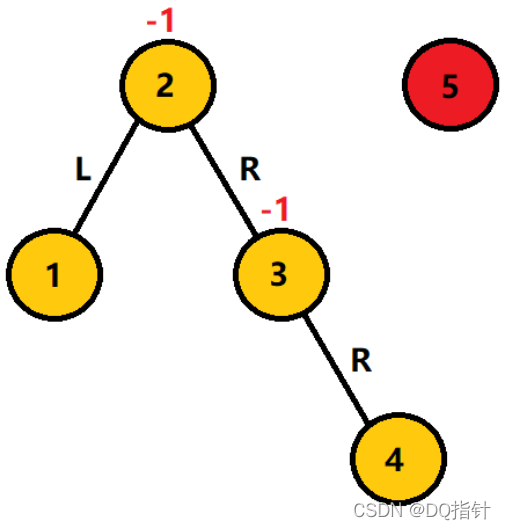
如图，在图中的平衡二叉搜索树中插入5结点。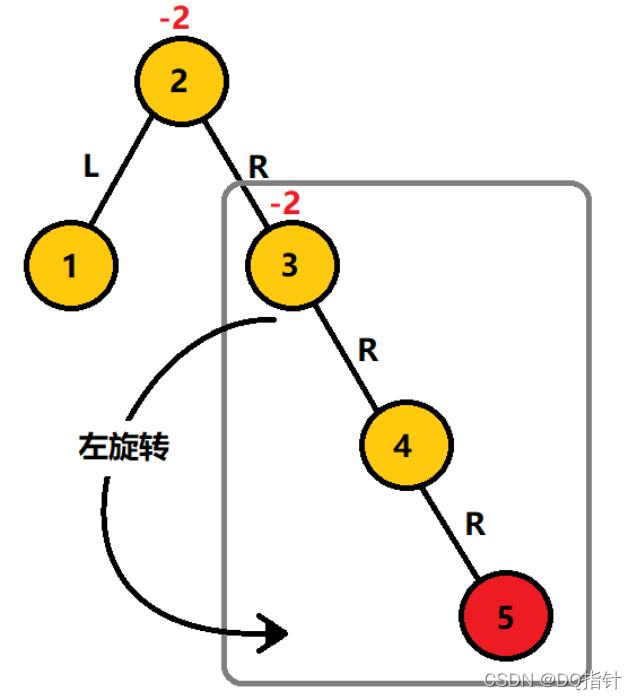

对于图中情况与右旋转正好相反，只需要对最小不平衡树（以3为根节点的二叉树）进行旋转，旋转后2结点的右子结点为4结点，3结点成为4结点的左子结点。旋转后如下。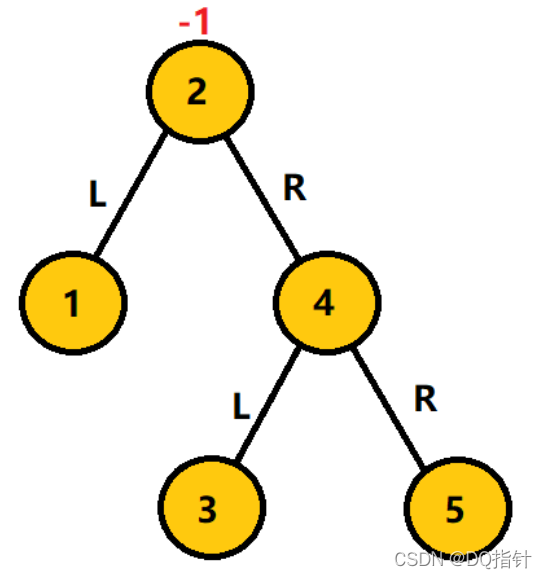

RR旋转（左旋转）伪代码：

//A为最低不平衡结点，B为A的右节点
AVLTree*LeftRotation(Node *A){/* 注意：A必须有一个右子结点B *//* 将A与B做左旋转，更新A与B的高度，返回新的根结点B */
    Node *B = A->Right;
    A->Right = B->Left;
    B->Left = A;/*GetHeight为获取高度的函数*/
    A->Height =max(GetHeight(A->Left),GetHeight(A->Right))+1;
    B->Height =max(GetHeight(B->Left),A->Height)+1;return B;//返回新的子树根节点，与父亲结点连接}

右左双旋转：

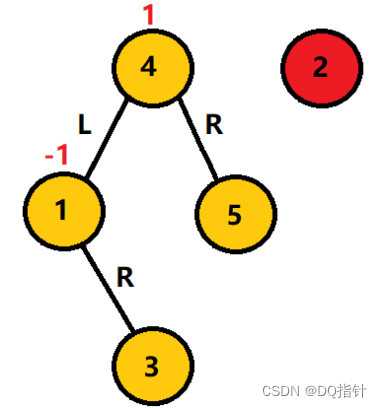
如图，我们要在图中的平衡二叉搜索树中插入结点2。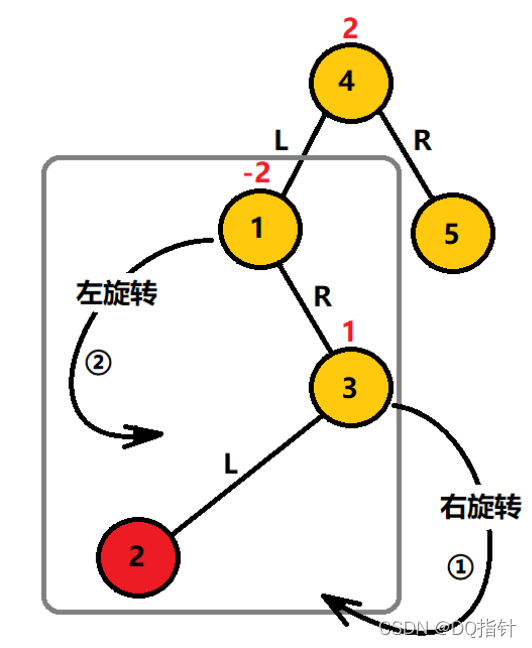

插入2结点后，灰色框中为最小不平衡二叉树，其不平衡是由子树根节点的右子树和右子树的左子树引起（在代码中由根节点和左子结点的高度因子判断），这种情况我们定义为RL型，因为是1的右子树的左子树引起的不平衡，需要先对这里的3结点进行右旋转使其变成RR型，再对1结点进行左旋转使其平衡。过程如下：

第一次3结点右旋转后，2结点成为1结点的右子结点，3结点成为2结点的右子结点，此时的二叉树为RR型，再将1结点左旋转1结点成为2结点的左子结点，最开始连结1结点的4结点此时连结2结点，这时二叉树平衡。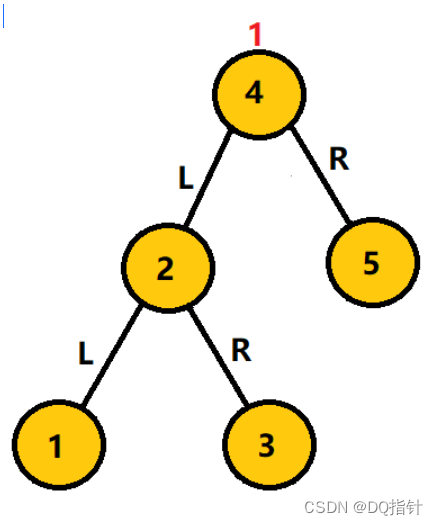

RL旋转（右左双旋转）伪代码：

AVLTree*RightLeftRotation(Node *A){ 
   Node* B = A->Left;
    A->Left =SingriRightRotation(B);//先对B结点右旋转，将A转化为RRreturnSingleLeftRotation(A);//先对A结点左旋转}

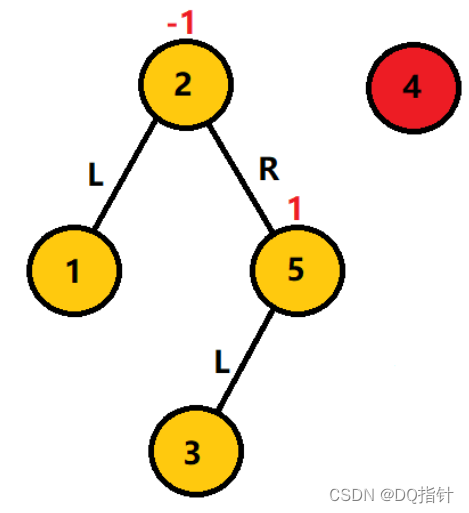
如图，我们要在图中的平衡二叉搜索树中插入结点4。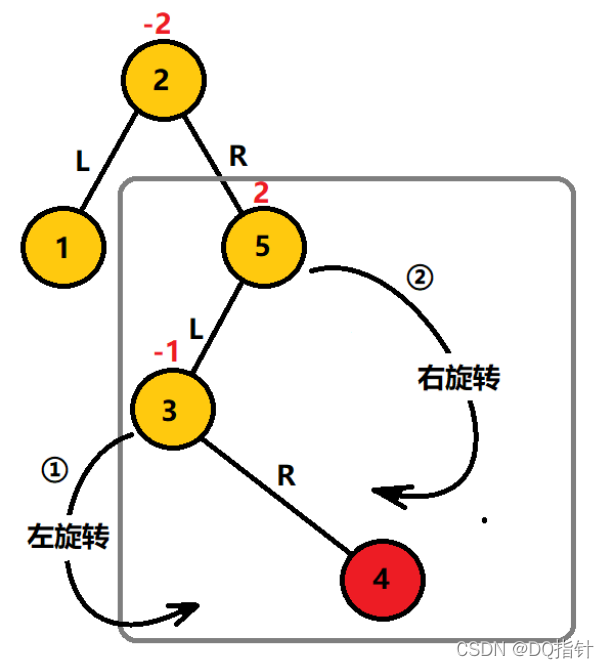

插入4结点后，灰色框中为最小不平衡二叉树，其不平衡是由5节点的左子树和左子树的右子树引起（在代码中由根节点和左子结点的高度因子判断），这种情况我们定义为LR型，需要先对这里的3结点进行左旋转使其变成LL型，再对5结点进行右旋转使其平衡。过程如下：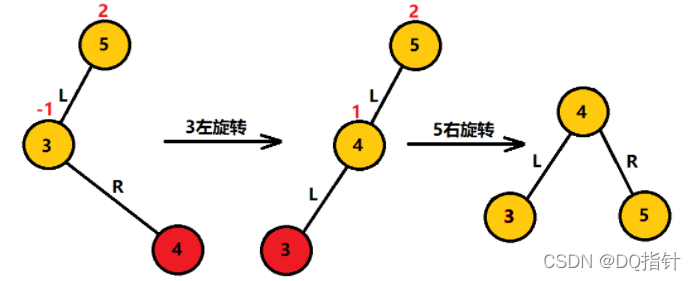
第一次3结点左旋转后，4结点成为5结点的左子结点，3结点成为4结点的左子结点，此时的二叉树为LL型，再将5结点右旋转5结点成为4结点的右子结点，最开始连结5结点的2结点此时连结4结点，这时二叉树平衡。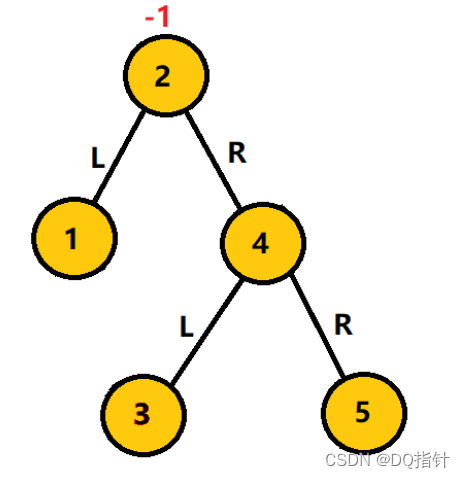

AVLTree*LeftRightRotation(Node *A){ 
    Node* B = A->Left;
    A->Left =SingriLeftRotation(B);//先对B结点左旋转，将A转化为LLreturnSingleRightRotation(A);//再对A结点右旋转}

添加新结点：

voidUpdateHeight(Node *rt){//更新高度      if(rt==NULL)return; 
    rt->height=max(GetHeight(rt->left),GetHeight(rt->right))+1;}boolInsertBST(Node *rt,int k){//插入 if(rt==NULL){
        rt=newNode(k);returntrue;}if(k==rt->val)returnfalse;bool res=true;//判断插入是否成功if(k<rt->val){
        res=InsertBST(rt->left,k);if(res&&GetHeight(rt->left)-GetHeight(rt->right)>1){if(k<rt->left->val)LeftRotation(rt);//左左elseLeftRightRotation(rt);//左右 }}else{
        res=InsertBST(rt->right,k);if(res&&GetHeight(rt->left)-GetHeight(rt->right)<-1){if(k>rt->right->val)RightRotation(rt);//右右 elseRightLeftRotation(rt);//右左 }}if(res)UpdateHeight(rt);//高度更新return res;}

删除结点：

voidDeleteBST_(Node *rt, Node *pt){//删除节点有左右子树时处理 if(rt->right==NULL){
        Node *p=rt;
        pt->val=rt->val;
        rt=rt->left;delete p;}else{DeleteBST_(rt->right,pt);if(GetHeight(rt->left)-GetHeight(rt->right)>1){LeftRotation(rt);//左左 }}UpdateHeight(rt);}boolDeleteBST(Node *rt,int k){//删除if(rt==NULL)returnfalse;bool res=true;if(rt->val==k){if(rt->left==NULL){
            rt=rt->right;}elseif(rt->right==NULL){
            rt=rt->left;}else{DeleteBST_(rt->left,rt);}}elseif(k<rt->val){
        res=DeleteBST(rt->left,k);//向目标值递归if(res&&GetHeight(rt->left)-GetHeight(rt->right)>1){//成功删除后调整二叉树if(k<rt->left->val)LeftRotation(rt);//左左elseLeftRightRotation(rt);//左右}elseif(res&&GetHeight(rt->left)-GetHeight(rt->right)<-1){if(k>rt->right->val)RightRotation(rt);//右右 elseRightLeftRotation(rt);//右左 }}else{
        res=DeleteBST(rt->right,k);//向目标值递归if(res&&GetHeight(rt->left)-GetHeight(rt->right)>1){//成功删除后调整二叉树if(k<rt->left->val)LeftRotation(rt);//左左elseLeftRightRotation(rt);//左右 }elseif(res&&GetHeight(rt->left)-GetHeight(rt->right)<-1){if(k>rt->right->val)RightRotation(rt);//右右 elseRightLeftRotation(rt);//右左 }}if(res)UpdateHeight(rt);return res;}

投稿来自 指针35期 - 东北石油大学 - 计科206 - 赵宇昊