FORD-FULKERSON算法

正文

本文主要讲解最大流问题的Ford-Fulkerson解法。可以说这是一种方法，而不是算法，因为它包含具有不同运行时间的几种实现。该方法依赖于三种重要思想：残留网络，增广路径和割。

在介绍着三种概念之前，我们先简单介绍下Ford-Fulkerson方法的基本思想。首先需要了解的是Ford-Fulkerson是一种迭代的方法。开始时，对所有的u,v属于V，f(u,v)=0(这里f(u,v)代表u到v的边当前流量)，即初始状态时流的值为0。在每次迭代中，可以通过寻找一个“增广路径”来增加流值。增广路径可以看做是从源点s到汇点t之间的一条路径，沿该路径可以压入更多的流，从而增加流的值。反复进行这一过程，直到增广路径都被找出为止，即得到最大的网络流。

举个例子来说明下，如图所示，每条线就代表了一条增广路径，当前s到t的流量为3。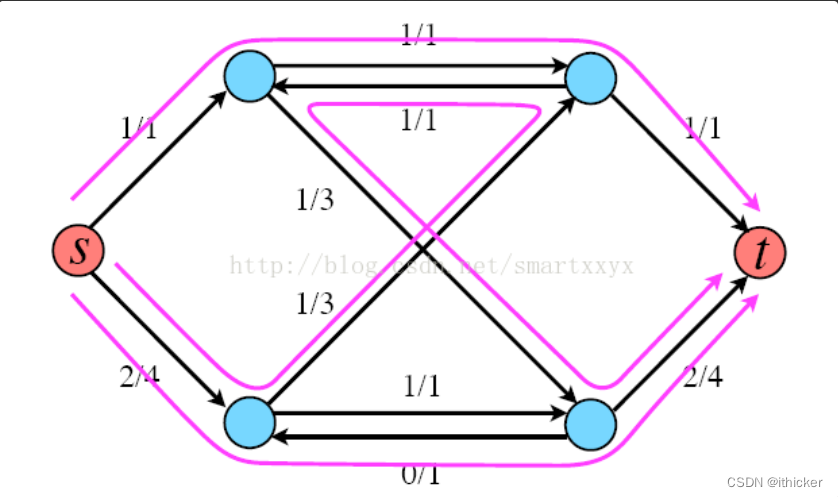
在这里插入图片描述
当然这并不是该网络的最大流，根据寻找增广路径的算法我们其实还可以继续寻找增广路径，最终的最大流网络如下图所示，最大流为4。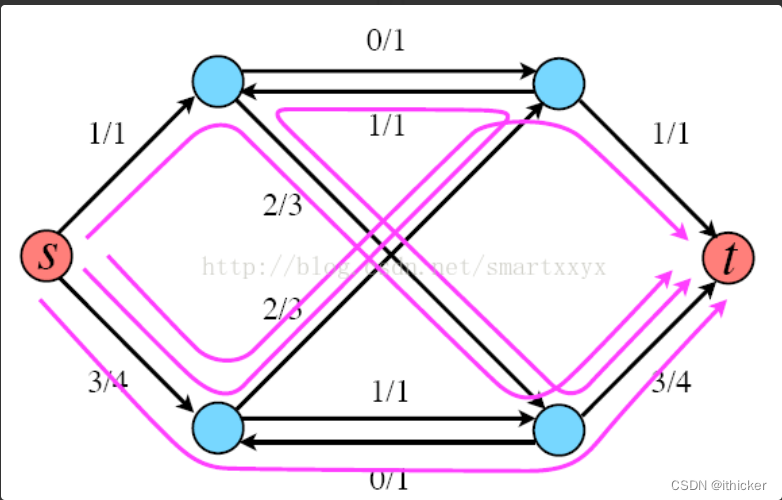

接下来我们就介绍如何寻找增广路径。在介绍增广路径之前，我们首先需要介绍残留网络的概念。

流网络

先来看流网络的定义。对于流网络，《算法导论》第26章是这样定义的：

流网络 G = (V, E)是一个有向图，图中每一条边(u, v) ∈ E有一个非负的容量值c(u, v) >=0。而且，如果边集合E包含一条边(u, v)，则图中不存在反方向的边(v, u)。如果(u, v) ∉ E，则为方便起见，定义c(u, v) = 0。并且在图中不允许自循环。在流网络的所有节点中，我们特别分辨出两个特殊节点：源节点s和汇点t。

下面我来用一个例子对这个定义进行解释。来看下面的这个有向图。图中的s为源节点(source)，t为汇点(sink)。 也就是说，对于顶点s，只能有以它为起点的边；而对于t，只能有以它为终点的边。 图中每个边上面的数字就是这条边的容量值c。例如，c(s, v) = 6。图中没有(s, z)这条边，因此c(s, z) = 0。图中不能有自循环边，也就是(s, s) 这样的边。我们用f(u, v)表示两个点之间的实际流量值。
在这里插入图片描述

残留网络

在这里插入图片描述

顾名思义，残留网络是指给定网络和一个流，其对应还可以容纳的流组成的网络。具体说来，就是假定一个网络G=（V，E），其源点s，汇点t。设f为G中的一个流，对应顶点u到顶点v的流。在不超过C（u，v）的条件下（C代表边容量），从u到v之间可以压入的额外网络流量，就是边（u，v）的残余容量（residual capacity），定义如下：

r（u，v）=c（u，v）-f（u，v）

举个例子，假设（u，v）当前流量为3/4，那么就是说c（u，v）=4，f（u，v）=3，那么r（u，v）=1。

我们知道，在网络流中还有这么一条规律。从u到v已经有了3个单位流量，那么从反方向上看，也就是从v到u就有了3个单位的残留网络，这时r（v，u）=3。可以这样理解，从u到v有3个单位流量，那么从v到u就有了将这3个单位流量的压回去的能力。

我们来具体看一个例子，如下图所示一个流网络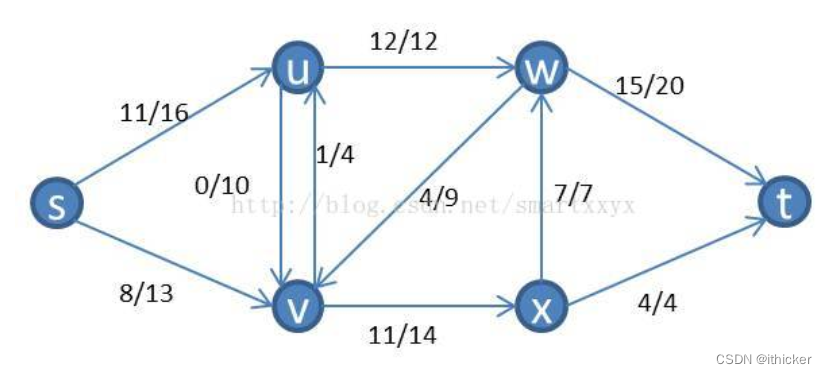
在这里插入图片描述
其对应的残留网络为：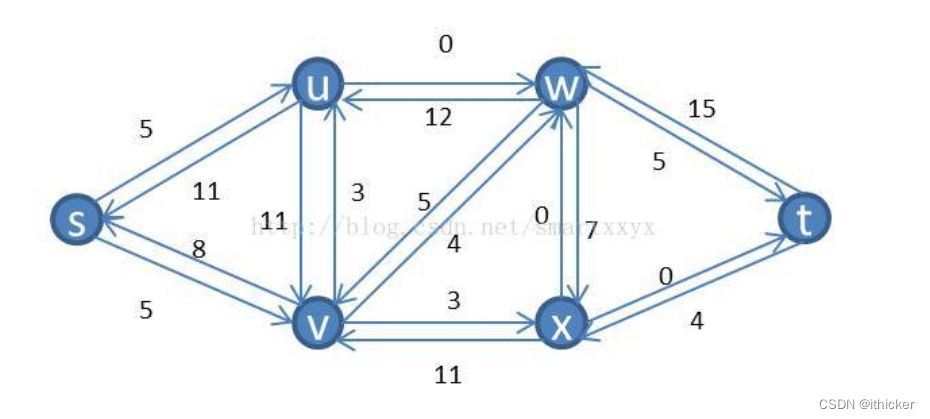

增广路径

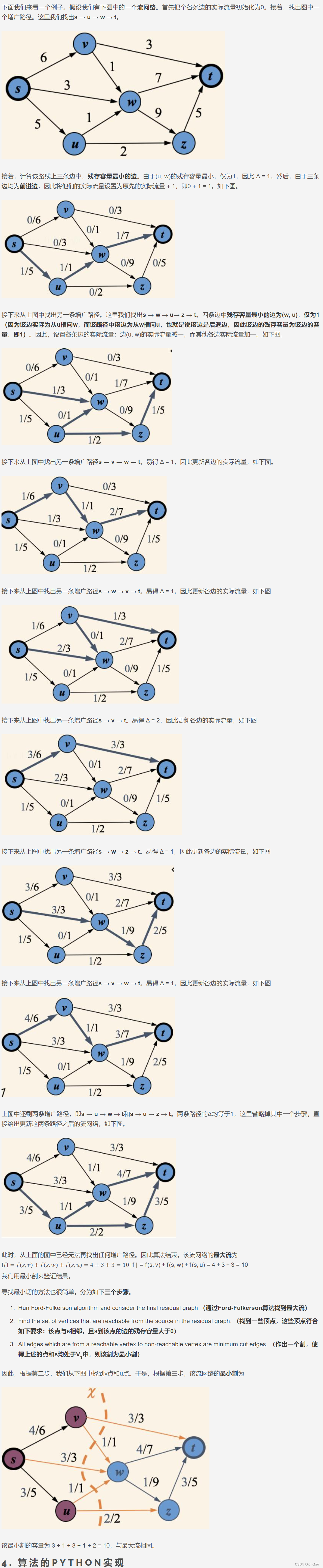
在了解了残留网络后，我们来介绍增广路径。已知一个流网络G和流f，增广路径p是其残留网络Gf中从s到t的一条简单路径。形象的理解为从s到t存在一条不违反边容量的路径，向这条路径压入流量，可以增加整个网络的流值。上面的残留网络中，存在这样一条增广路径：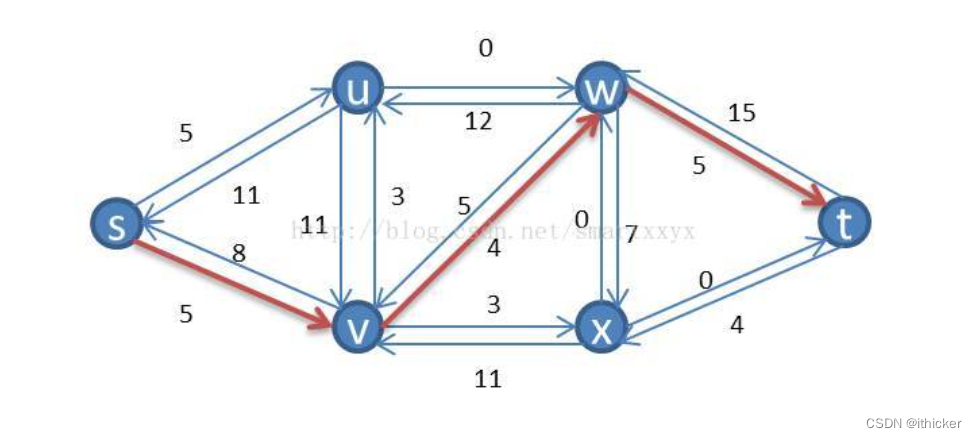
在这里插入图片描述
其可以压入4个单位的流量，压入后，我们得到一个新的流网络，其流量比原来的流网络要多4。这时我们继续在新的流网络上用同样的方法寻找增广路径，直到找不到为止。这时我们就得到了一个最大的网络流。

流网络的割

上面仅仅是介绍了方法，可是怎么证明当无法再寻找到增广路径时，就证明当前网络是最大流网络呢？这就需要用到最大流最小割定理。

首先介绍下，割的概念。流网络G（V，E）的割（S，T）将V划分为S和T=V-S两部分，使得s属于S，t属于T。割（S，T）的容量是指从集合S到集合T的所有边（有方向）的容量之和（不算反方向的，必须是S-àT）。如果f是一个流，则穿过割（S，T）的净流量被定义为f（S，T）（包括反向的，SàT的为正值，T—>S的负值）。将上面举的例子继续拿来，随便画一个割，如下图所示：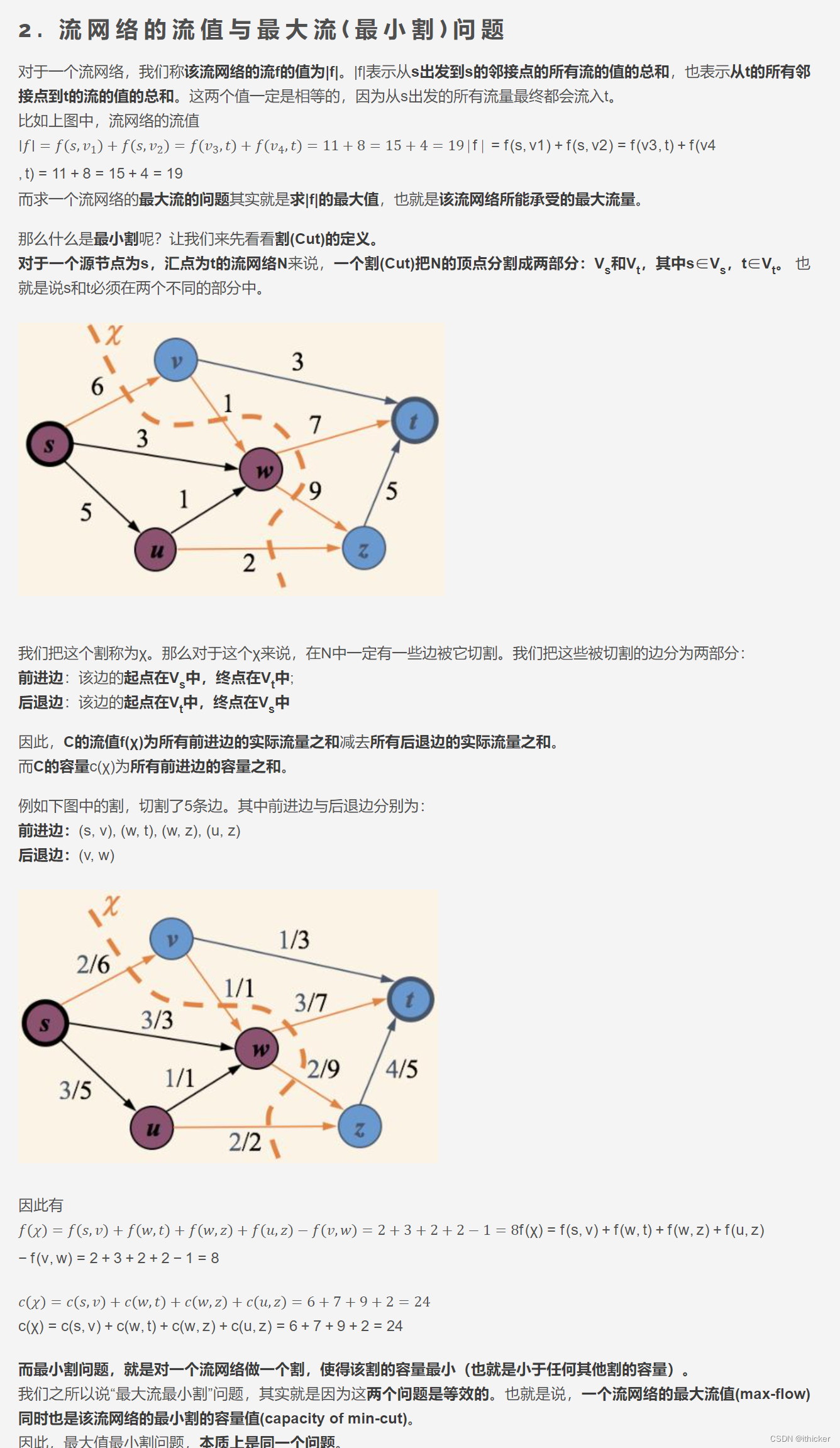
在这里插入图片描述

显然，我们有对任意一个割，穿过该割的净流量上界就是该割的容量，即不可能超过割的容量。所以网络的最大流必然无法超过网络的最小割。最小割是指割的容量最小，最大流是指网络当中最大的净流量，简单的例子s是水龙头源源不断往外排出水，这些边相当于管道，各管道的容量不容，在某一段的容量我们其实用割来表示，最小割就是在整体管道系统当中我们找到的最窄处也就是某一段管道流量最小处，而我们的水流流过某一阶段所有水流的总量用流量来表示，最大流就是我们通过该管道是某一阶段水的总量最多为多少，若超过了这个最大流量就会导致超过管道某一阶段的容量，就爆炸了，所以我们若想保证水流可以从s流到t，则必须保证水流流量也就是最大流要小于等于最小割，但是为了让水尽快流过去，所以我们要使最大流等于最小割，所以在求最优化的过程中，求最大流等效于求最小割，两者本质上是同一个问题。

可是，这跟残留网络上的增广路径有什么关系呢？

首先，我们必须了解一个特性，根据上一篇文章中讲到的最大流问题的线性规划表示时，提到，流网络的流量守恒的原则，根据这个原则我们可以知道，对网络的任意割，其净流量的都是相等的。具体证明是不难的，可以通过下图形象的理解下，
在这里插入图片描述
和上面的割相比，集合S中少了u和v，从源点s到集合T的净流量都流向了u和v，而在上一个割图中，集合S到集合T的流量是等于u和v到集合T的净流量的。其中w也有流流向了u和v，而这部分流无法流向源点s，因为没有路径，所以最后这部分流量加上s到u和v的流量，在u和v之间无论如何互相传递流，最终都要流向集合T，所以这个流量值是等于s流向u和v的值的。将s比喻成一个水龙头，u和v流向别处的水流，都是来自s的，其自身不可能创造水流。所以任意割的净流量都是相等的，割的净流量就是流量，求到最大时就是最大流且等于最小割，也就是流量守恒性质，各处流量相等