《Python 计算机视觉编程》学习笔记（一）

《Python计算机视觉编程》

文章目录

前言

计算机视觉是一门对图像中信息进行自动提取的学科。

计算机视觉有时试图模拟人类视觉，有时使用数据和统计方法，而有时几何是解决问题的关键。

第 1 章基本的图像操作和处理

引言

1.1 PIL： Python图像处理类库

PIL（ Python Imaging Library Python，图像处理类库）提供了通用的图像处理功能，以及大量有用的基本图像操作。

图像读取、显示、显示对应灰度图

from PIL import Image
from time import*defmain():# 读取一幅图像
    pil_im = Image.open('empire.jpg')# 读取一幅图像，并将其转换成灰度图像，
    pil_imL = Image.open('empire.jpg').convert('L')
    pil_im.show()
    pil_imL.show()returnif __name__ =='__main__':

    timeStart = time()
    main()
    timeOver = time()print("program running time is :",timeOver - timeStart)

原图如下：
在这里插入图片描述
程序运行后输出结果如下：

一张为正常彩色图片，一张为转换后的灰度图片。
我使用的Python版本为3.8所以书中的代码没法直接使用，需要调整一下。

更改图像格式（后缀）

defchangeFormat():""" 
        函数功能：修改图像格式
        参数说明：无
        函数返回：无
    """

    filelist = get_imlist(r"D:\python\exercise_data\ComputerVision\ch01\figure")# 遍历整个文件夹查找出路径中符合条件的图像文件for infile in filelist:# 对原图像文件的格式进行修改
        outfile = os.path.splitext(infile)[0]+'.png'# 判断是否修改成功，成功则进行save()方法if infile !=outfile:try:
                Image.open(infile).save(outfile)except IOError:print("cannot convert",infile)returndefmain():# readAndShow()
    changeFormat()returnif __name__ =='__main__':

    timeStart = time()
    main()
    timeOver = time()print("program running time is :",timeOver - timeStart)

在这里插入图片描述
程序实际上是将图片读取，然后修改名称后缀，之后保存。

创建缩略图

defthumbnail():""" 
        函数功能：生成缩略图
        参数说明：无
        函数返回：无
    """
    op_image = Image.open(r'./figure/empire.jpg')

    plt.subplot(121)
    plt.imshow(op_image)
    plt.title("original")# 输出原图
    op_image.thumbnail((128,128))#图像缩略处理，指定大小为128*128 
    plt.subplot(122)
    plt.imshow(op_image)
    plt.title("result")

    plt.show()return

输出如下：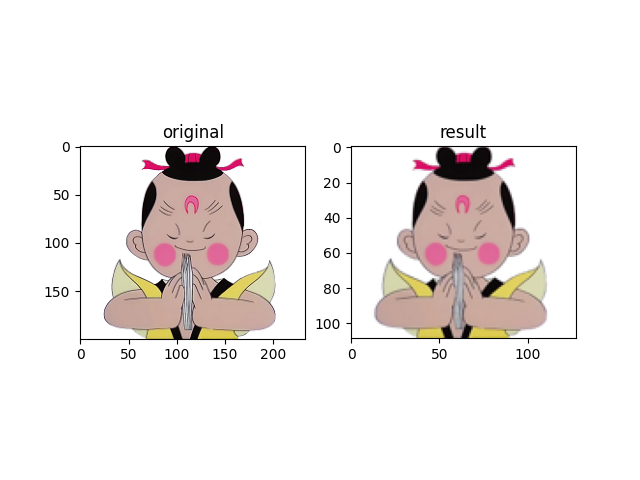
在这里插入图片描述

对比上图，不难发现缩略后的图片看起来比较模糊，而且坐标尺寸也小于原图。

复制和粘贴图像区域

defcopyAndPaste(op_image):""" 
        函数功能：复制粘贴一幅图片中的部分内容
        参数说明：op_image__已打开的图片
        函数返回：无
    """

    box =(50,50,200,200)# 元组给出裁剪区域
    re_img = op_image.crop(box)# 利用crop方法进行图片裁剪
    axes = subplot(121)
    imshow(op_image), title("original")
    
    subplot(122)
    imshow(re_img), title("result")
    show()returndefmain(): 
    op_image = Image.open(r'./figure/empire.jpg')# readAndShow()# changeFormat()# thumbnail()
    copyAndPaste(op_image)return

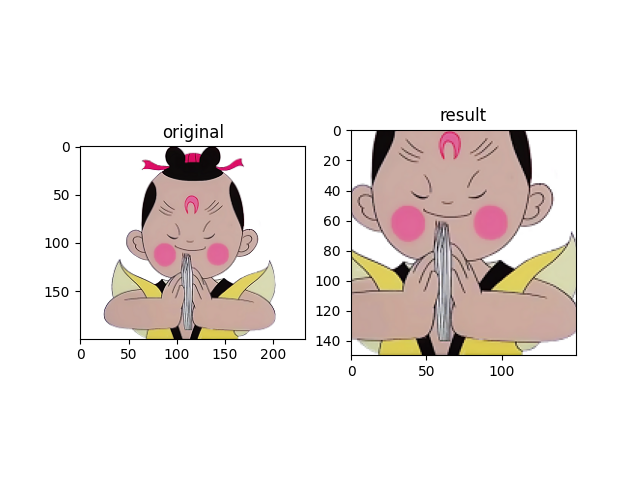
在这里插入图片描述

上图可以看到输出结果为原图的部分，对比坐标就是 (50, 50，200, 200) 四条线包围的部分。

调整尺寸和旋转

defadjustAndRotate(or_image):""" 
        函数功能：调整图片尺寸和旋转
        参数说明：or_image__已打开的图片
        函数返回：无
    """

    size =(128,128)# resize()用以调整图片的大小，参数为元组
    out_image1 = or_image.resize(size)# rotate()用以对图像进行旋转，参数为（0-360）
    out_image2 = or_image.rotate(180)
    
    subplot(131)
    imshow(or_image), title('original')
   
    subplot(132)
    imshow(out_image1), title('resize')
    
    subplot(133)
    imshow(out_image2), title('rotate')
    
    show()return

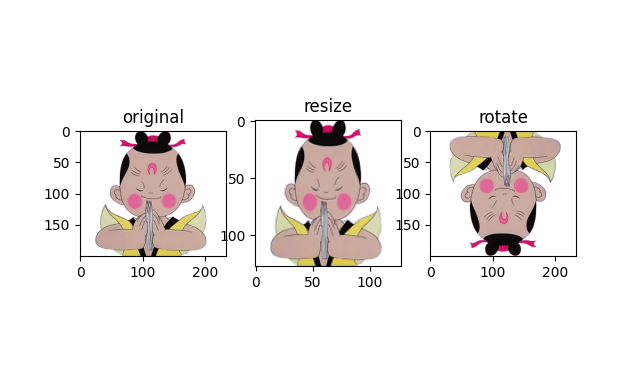
在这里插入图片描述
上图分别展示的是原图、调整了尺寸的图像，可以看到坐标有差异。最后是将图片旋转了90度后的图片。

1.2 Matplotlib

Matplotlib是个很好的类库，具有比 PIL 更强大的绘图功能。

绘制图像、点和线

defplotPointAndLine(or_image):""" 
    函数功能：在绘制的图片上绘制线
    参数说明：or_image__已打开的图片
    函数返回：无
    """# 将图像转换为数组
    img = array(or_image)
 
    imshow(img)
 
    x =[10,50,100,200]
    y =[20,50,150,180]# 根据给出的坐标绘制红色点
    plot(x, y,"r*")# 绘制连接4个点的线
    plot(x[:4], y[:4])
    title('plotting')
    show()return

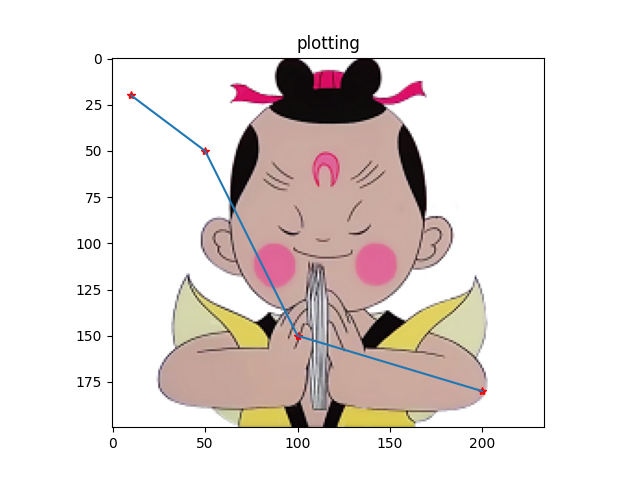
在这里插入图片描述
如上图所示，底图是“蛋生”，蛋生上的线条就是我们绘制的线条。
加了坐标轴看起来可能不舒服，我们就使用 axis(‘off’)来关闭坐标轴。

# 将图像转换为数组
 img = array(or_image)
 imshow(img)
 x =[10,50,100,200]
 y =[20,50,150,180]# 根据给出的坐标绘制红色点
 plot(x, y,"r*")# 绘制连接4个点的线
 plot(x[:4], y[:4])
 title('plotting')
 axis('off')
 show()

使用还是之前的代码，增加一行就可以。输出结果如下：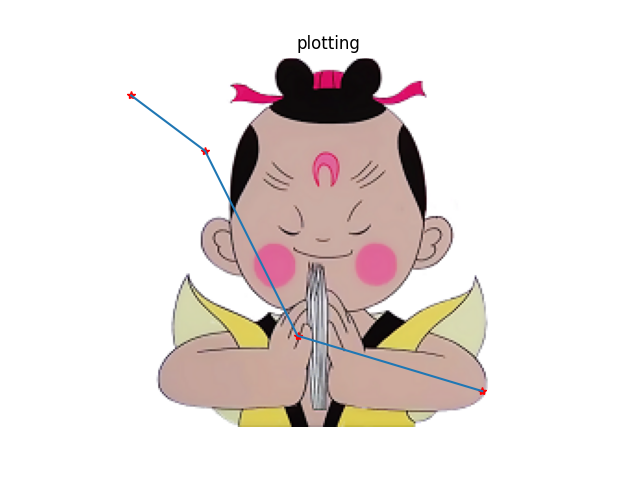
在这里插入图片描述
此时照片就不含有坐标轴。

图像轮廓和直方图

defoutlineAndHistogram(fileName):""" 
    函数功能：绘制图像轮廓和直方图
    参数说明：fileName__图像存储路径
    函数返回：无
    """# 读取图像至数组中,并将其转为灰度图像
    im = array(Image.open(fileName).convert('L'))
    re_im = Image.open(fileName)
    
    subplot(131)
    imshow(re_im), title('original')
    
    subplot(132)
    gray()# 不使用颜色信息
    contour(im, origin='image')# 在原点的左上角显示轮廓图像
    axis('off')
    axis('equal')

    subplot(133)# 直方图绘制# flatten() 方法将任意数组按照行优先准则转换成一维数组。
    hist(im.flatten(),128)
    show()return

输出如下：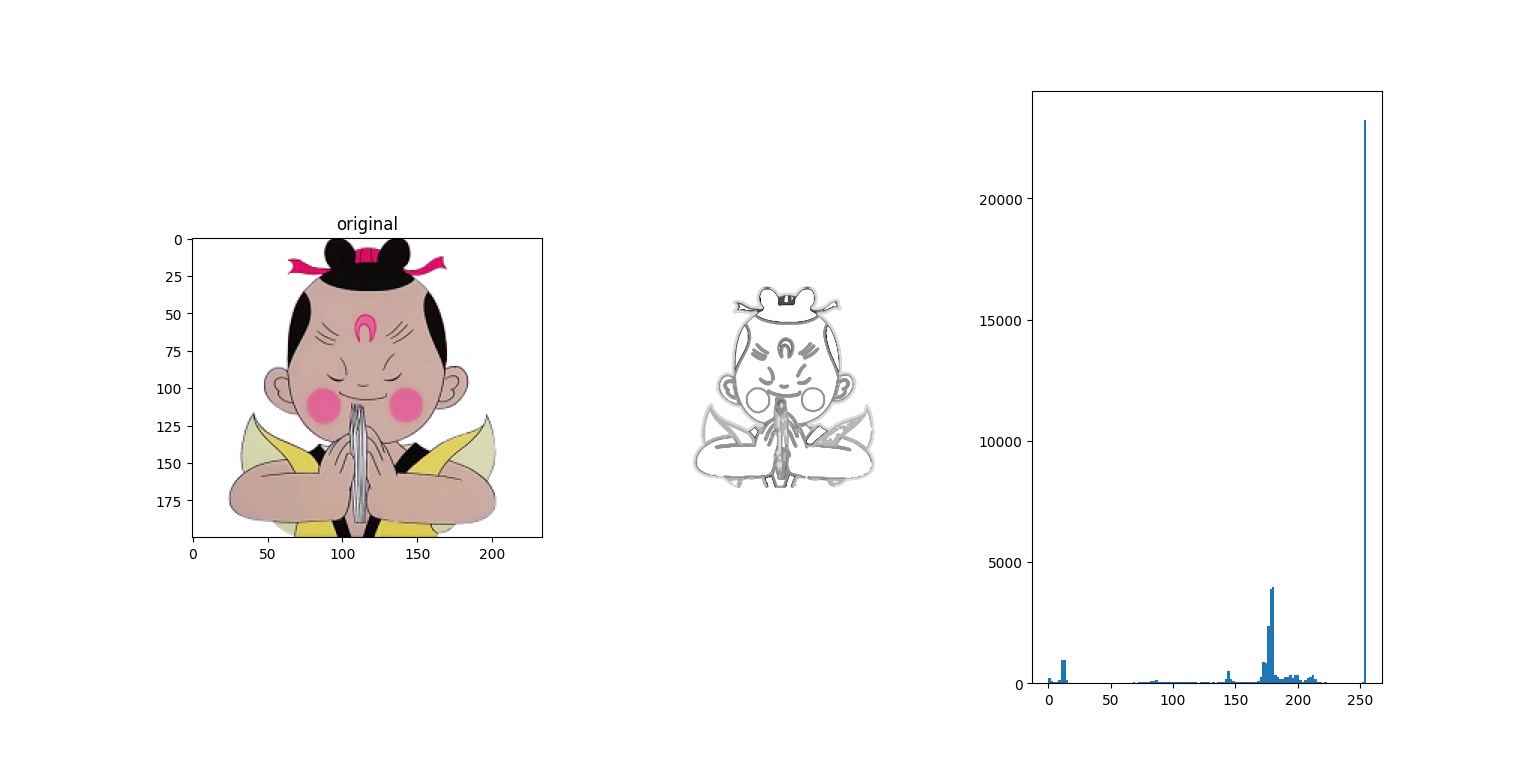
在这里插入图片描述
最左侧的是原图，中间的是原图对应的轮廓线，我们可以清晰的看到。最右侧的是图像对饮过得直方图的统计。可以大致得到图像灰度值的分部。

交互式标注

defmarkPoint(fileName):""" 
    函数功能：给出点击点的坐标
    参数说明：fileName__图像存储路径
    函数返回：无
    """
    im = array(Image.open(fileName))
    imshow(im)while(True):print("please click 3 points")
        x = ginput(3)print("you click:", x)
        matData = mat(x)# 这里取得是列所以要转
        axis_x = matData[:,0]
        axis_y = matData[:,1]# [item[i] for item in a]

        plot(axis_x.flatten(), axis_y.flatten(),"o")# 三个点的横坐标过近时，就退出
        pointDistance = axis_x[0][0]-axis_x[1][0]+axis_x[2][0]-axis_x[1][0]if pointDistance <100:print('quit :',pointDistance)break
    show()return

输出结果如下：
在这里插入图片描述
图像上三个桔绿蓝的点是我们点点击的位置，程序输出的位置为：

[(74.50865800865802,69.19696969696969),(142.04112554112555,95.17099567099567),(83.59956709956711,121.57792207792207)]

目测一下坐标是对的上的。

1.3 NumPy

Numpy是非常有名的 Python 科学计算工具包，其中包含了大量有用的思想，比如数组对象（用来表示向量、矩阵、图像等）以及线性代数函数。

图像数组表示

defimageArray(fileName):""" 
    函数功能：图像数组表示
    参数说明：fileName__图像存储路径
    函数返回：无
    """
    img0 = array(Image.open(fileName))print(img0.shape, img0.dtype)
    img = array(Image.open(fileName).convert('RGB'))# RGBprint(img.shape, img.dtype)
    img1 = array(Image.open(fileName).convert('1'))# 二值图像非0即1，故数据类型为bool型print(img1.shape, img1.dtype)
    img2 = array(Image.open(fileName).convert('L'))# 灰度图，灰度值在0-255之间，且为设定其数据类型，array自动判定为uint8型print(img2.shape, img2.dtype)
    img3 = array(Image.open(fileName).convert('L'),'f')# 灰度图，‘f’设定其数据类型为float类型，故显示为float32print(img3.shape, img3.dtype)return

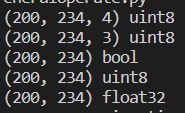
在这里插入图片描述
输出与注释一致。就是将图片信息按照我们的要求读取出来后，存储到一个数组中，彩色图像是三维数组，因为包含RGB三色。灰度图像就是二维数组。每一个点代表图像中的每一个像素点。所以我们访问图片数组就是在访问每一个像素点。

灰度变换

defgrayChange(fileName):""" 
    函数功能：图像灰度变换
    参数说明：fileName__图像存储路径
    函数返回：无
    """
    or_img = array(Image.open(fileName))# 灰度变换
    gr_img = array(Image.open(fileName).convert('L'))# 对灰度图进行反相处理
    gr_img1 =255- gr_img
    # 将图像的像素转变到100-200区间
    gr_img2 =(100.0/255)* gr_img +100# 将灰度图像的像素求平方
    gr_img3 =255.0*(gr_img/255.0)**2
    
    subplot(231)
    imshow(or_img), title('origin')
   
    subplot(232)
    gray()  
    imshow(gr_img), title('gray')
    
    subplot(233)
    gray()  
    imshow(gr_img1), title('gray_re')
    
    subplot(234)
    gray()  
    imshow(gr_img2), title('gray(100-200)')
    
    subplot(235)
    imshow(gr_img3), title('gray**2')
    show()return

输出如下：
在这里插入图片描述
如上图所示，展示的为从原图变换后得到的各种灰度图。按从左往右，从上往下的顺序，原图之后是灰度图，直接调用程序中的转换函数得到。接下来是反相，可以看到在灰度图中暗的部分现在变成了亮色，而原本亮的地方这里变成了黑色。接下来是对灰度值进行了一个归一化，变化到100-200范围内，可以发现图片的对比度有了提升，原本暗的地方更暗，亮的地方也更亮。最后一个是对灰度值进行了平方操作，整体图像更加偏暗了。

直方图均衡化

直方图均衡化是指将一幅图像的灰度直方图变平，使变换后的图像中每个灰度值的分布概率都相同。在对图像做进一步处理之前，直方图均衡化通常是对图像灰度值进行归一化的一个非常好的方法，并且可以增强图像的对比度。之前的灰度变换中将灰度值变到100-200就能看到。

直方图均衡化的变换函数是图像中像素值的累积分布函数（ cumulative distribution function，简写为 cdf，将像素值的范围映射到目标范围的归一化操作）。

defhistequal(fileName):""" 
    函数功能：直方图均衡化
    参数说明：fileName__图像存储路径
    函数返回：无
    """
    img = array(Image.open(fileName).convert('L'))
    img2, cdf = histeq(img)
   
    subplot(231)
    hist(img.flatten(),128)

    subplot(234)
    gray()
    imshow(img), title('gray')
    
    subplot(233)
    hist(img2.flatten(),128)
    
    subplot(232)
    gray()
    plot(cdf,'b-')

    subplot(236)
    gray()
    imshow(img2), title('gray_ch')
    show()return

输出如下：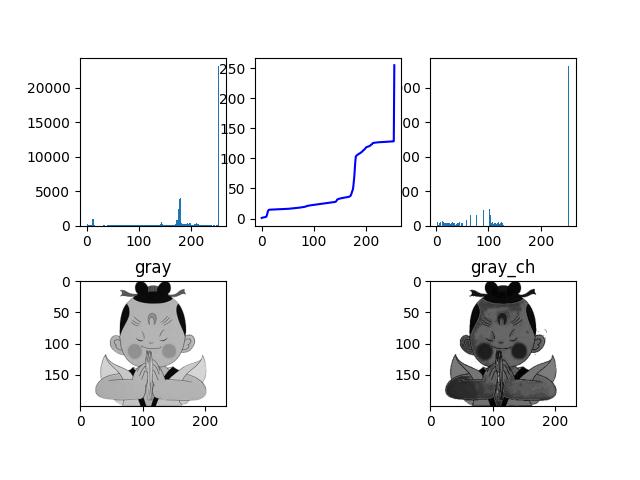
在这里插入图片描述

左侧为原始图像和直方图，中间图为灰度变换函数，右侧为直方图均衡化后的图像和相应直方图。明显差异就是均衡过后的图像对比度变大。

图像平均操作是减少图像噪声的一种简单方式，通常用于艺术特效。

图像的主成分分析（ PCA）

PCA（ Principal Component Analysis，主成分分析）是一个非常有用的降维技巧。它可以在使用尽可能少维数的前提下，尽量多地保持训练数据的信息
这部分可以参考《机器学习实战》利用PCA来简化数据这里面有PCA更详细的说明。区别在于我们现在在分析图片，而里面是对于矩阵的处理。

1.4 SciPy

SciPy是建立在 NumPy 基础上，用于数值运算的开源工具包。SciPy 提供很多高效的操作，可以实现数值积分、优化、统计、信号处理，以及对我们来说最重要的图像处理功能。

图像模糊

图像的高斯模糊是非常经典的图像卷积例子。本质上，图像模糊就是将（灰度）图像 I 和一个高斯核进行卷积操作：

其中 * 表示卷积操作； Gσ 是标准差为 σ 的二维高斯核，定义为 :

       I
      
      
       σ
      
     
     
      =
     
     
      I
     
     
      ∗
     
     
      
       G
      
      
       σ
      
     
    
    
     \boldsymbol{I}_{\sigma}=\boldsymbol{I} * G_{\sigma}
    
   
  Iσ=I∗Gσ

其中 * 表示卷积操作；

     G
    
    
     σ
    
   
  
  
   G_σ
  
 
Gσ 是标准差为 σ 的二维高斯核，定义为 :

  
   
    
     
      
       G
      
      
       σ
      
     
     
      =
     
     
      
       1
      
      
       
        2
       
       
        π
       
       
        σ
       
      
     
     
      
       e
      
      
       
        −
       
       
        
         (
        
        
         
          x
         
         
          2
         
        
        
         +
        
        
         
          y
         
         
          2
         
        
        
         )
        
       
       
        /
       
       
        2
       
       
        
         σ
        
        
         2
        
       
      
     
    
    
     G_{\sigma}=\frac{1}{2 \pi \sigma} \mathrm{e}^{-\left(x^{2}+y^{2}\right) / 2 \sigma^{2}}
    
   
  Gσ=2πσ1e−(x2+y2)/2σ2

defdimImage(fileName):""" 
    函数功能：直方图均衡化
    参数说明：fileName__图像存储路径
    函数返回：无
    """# 灰度图像的模糊处理
    img = array(Image.open(fileName).convert('L'))
    img_re0 = filters.gaussian_filter(img,2)
    img_re1 = filters.gaussian_filter(img,5)
    img_re2 = filters.gaussian_filter(img,10)# 彩色图像的模糊处理
    img_or = array(Image.open(fileName))

    img_or2 = zeros(img_or.shape)# guassian_filter() 函数的最后一个参数表示标准差
    img_or2= filters.gaussian_filter(img_or,1)
    
    img_or2 = uint8(img_or2)
    
    subplot(231)
    imshow(img_or), title('original')

    subplot(233)
    imshow(img_or2), title('rgb——1')

    subplot(234)
    gray()
    imshow(img_re1), title('gray——2')
    
    subplot(235)
    gray()
    imshow(img_re2), title('gray——5')
    
    subplot(236)
    gray()
    imshow(img_re2), title('gray——10')
    
    show()

输出如下：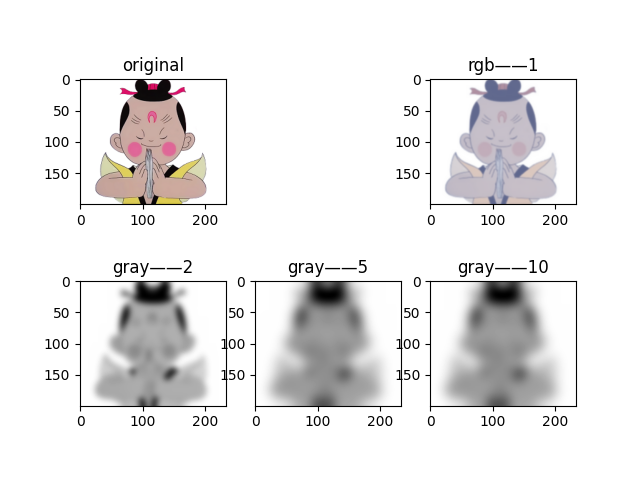
在这里插入图片描述
从上图可知随着 σ 的增加，一幅图像被模糊的程度越大。σ越大，处理后的图像细节丢失越多。

图像导数

在很多应用中图像强度的变化情况是非常重要的信息。强度的变化可以用灰度图像

    I
   
  
  
   I
  
 
I（对于彩色图像，通常对每个颜色通道分别计算导数）的x和y方向导数

 
  
   
    
     I
    
    
     x
    
   
  
  
   I_x
  
 
Ix和

 
  
   
    
     I
    
    
     y
    
   
  
  
   I_y
  
 
Iy进行描述。图像的梯度向量为
 
  
   
    
     ∇
    
    
     I
    
    
     =
    
    
     
      
       [
      
      
       
        I
       
       
        x
       
      
      
       ,
      
      
       
        I
       
       
        y
       
      
      
       ]
      
     
     
      T
     
    
   
   
    \nabla \boldsymbol{I}=\left[\boldsymbol{I}_{x}, \boldsymbol{I}_{y}\right]^{T}
   
  
 ∇I=[Ix,Iy]T。梯度有两个重要的属性，一是梯度的大小：
  
   
    
     
      ∣
     
     
      ∇
     
     
      I
     
     
      ∣
     
     
      =
     
     
      
       
        
         I
        
        
         x
        
        
         2
        
       
       
        +
       
       
        
         I
        
        
         y
        
        
         2
        
       
      
     
    
    
     |\nabla \boldsymbol{I}|=\sqrt{\boldsymbol{I}_{x}^{2}+\boldsymbol{I}_{y}^{2}}
    
   
  ∣∇I∣=Ix2+Iy2它描述了图像强度变化的强弱，一是梯度的角度：

  
   
    
     
      α
     
     
      =
     
     
      arctan
     
     
      ⁡
     
     
      2
     
     
      
       (
      
      
       
        I
       
       
        y
       
      
      
       ,
      
      
       
        I
       
       
        x
       
      
      
       )
      
     
    
    
     \alpha=\arctan 2\left(\boldsymbol{I}_{y}, \boldsymbol{I}_{x}\right)
    
   
  α=arctan2(Iy,Ix)

描述了图像中在每个点（像素）上强度变化最大的方向。

我们可以用离散近似的方式来计算图像的导数。图像导数大多数可以通过卷积简单地实现：

       I
      
      
       x
      
     
     
      =
     
     
      I
     
     
      ∗
     
     
      
       D
      
      
       x
      
     
     
       和 
     
     
      
       I
      
      
       y
      
     
     
      =
     
     
      I
     
     
      ∗
     
     
      
       D
      
      
       y
      
     
    
    
     \boldsymbol{I}_{x}=\boldsymbol{I} * D_{x} \text { 和 } \boldsymbol{I}_{y}=\boldsymbol{I} * D_{y}
    
   
  Ix=I∗Dx 和 Iy=I∗Dy

对于

     D
    
    
     x
    
   
  
  
   D_x
  
 
Dx和

 
  
   
    
     D
    
    
     y
    
   
  
  
   D_y
  
 
Dy ，通常选择 Prewitt 滤波器：

  
   
    
     
      
       D
      
      
       x
      
     
     
      =
     
     
      
       [
      
      
       
        
         
          
           
            −
           
           
            1
           
          
         
        
        
         
          
           0
          
         
        
        
         
          
           1
          
         
        
       
       
        
         
          
           
            −
           
           
            1
           
          
         
        
        
         
          
           0
          
         
        
        
         
          
           1
          
         
        
       
       
        
         
          
           
            −
           
           
            1
           
          
         
        
        
         
          
           0
          
         
        
        
         
          
           1
          
         
        
       
      
      
       ]
      
     
     
       和 
     
     
      
       D
      
      
       y
      
     
     
      =
     
     
      
       [
      
      
       
        
         
          
           
            −
           
           
            1
           
          
         
        
        
         
          
           
            −
           
           
            1
           
          
         
        
        
         
          
           
            −
           
           
            1
           
          
         
        
       
       
        
         
          
           0
          
         
        
        
         
          
           0
          
         
        
        
         
          
           0
          
         
        
       
       
        
         
          
           1
          
         
        
        
         
          
           1
          
         
        
        
         
          
           1
          
         
        
       
      
      
       ]
      
     
    
    
     D_{x}=\left[\begin{array}{lll} -1 & 0 & 1 \\ -1 & 0 & 1 \\ -1 & 0 & 1 \end{array}\right] \text { 和 } D_{y}=\left[\begin{array}{rrr} -1 & -1 & -1 \\ 0 & 0 & 0 \\ 1 & 1 & 1 \end{array}\right]
    
   
  Dx=⎣⎡−1−1−1000111⎦⎤ 和 Dy=⎣⎡−101−101−101⎦⎤

或者 Sobel 滤波器：

       D
      
      
       x
      
     
     
      =
     
     
      
       [
      
      
       
        
         
          
           
            −
           
           
            1
           
          
         
        
        
         
          
           0
          
         
        
        
         
          
           1
          
         
        
       
       
        
         
          
           
            −
           
           
            2
           
          
         
        
        
         
          
           0
          
         
        
        
         
          
           2
          
         
        
       
       
        
         
          
           
            −
           
           
            1
           
          
         
        
        
         
          
           0
          
         
        
        
         
          
           1
          
         
        
       
      
      
       ]
      
     
     
       和 
     
     
      
       D
      
      
       y
      
     
     
      =
     
     
      
       [
      
      
       
        
         
          
           
            −
           
           
            1
           
          
         
        
        
         
          
           
            −
           
           
            2
           
          
         
        
        
         
          
           
            −
           
           
            1
           
          
         
        
       
       
        
         
          
           0
          
         
        
        
         
          
           0
          
         
        
        
         
          
           0
          
         
        
       
       
        
         
          
           1
          
         
        
        
         
          
           2
          
         
        
        
         
          
           1
          
         
        
       
      
      
       ]
      
     
    
    
     D_{x}=\left[\begin{array}{lll} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{array}\right] \text { 和 } D_{y}=\left[\begin{array}{ccc} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end{array}\right]
    
   
  Dx=⎣⎡−1−2−1000121⎦⎤ 和 Dy=⎣⎡−101−202−101⎦⎤

defrepresentativeFilters(fileName):""" 
    函数功能：典型滤波
    参数说明：fileName__图像存储路径
    函数返回：无
    """

    img = array(Image.open(fileName).convert('L'))# Sobel滤波器
    img_x = zeros(img.shape)# sobel() 函数的第二个参数表示选择 x 或者 y 方向导数，第三个参数保存输出的变量。
    imgX = filters.sobel(img,1, img_x)
    img_y = zeros(img.shape)
    imgY = filters.sobel(img,0, img_y)# 梯度
    magnitude = sqrt(img_x**2+img_y**2)
    subplot(221)
    imshow(img, cmap='gray'), title('original')
    subplot(222)
    imshow(imgX, cmap='gray'), title('x')
    subplot(223)
    imshow(imgY, cmap='gray'), title('y')
    subplot(224)
    imshow(magnitude, cmap='gray'), title('magnitude')
    show()return

输出如下：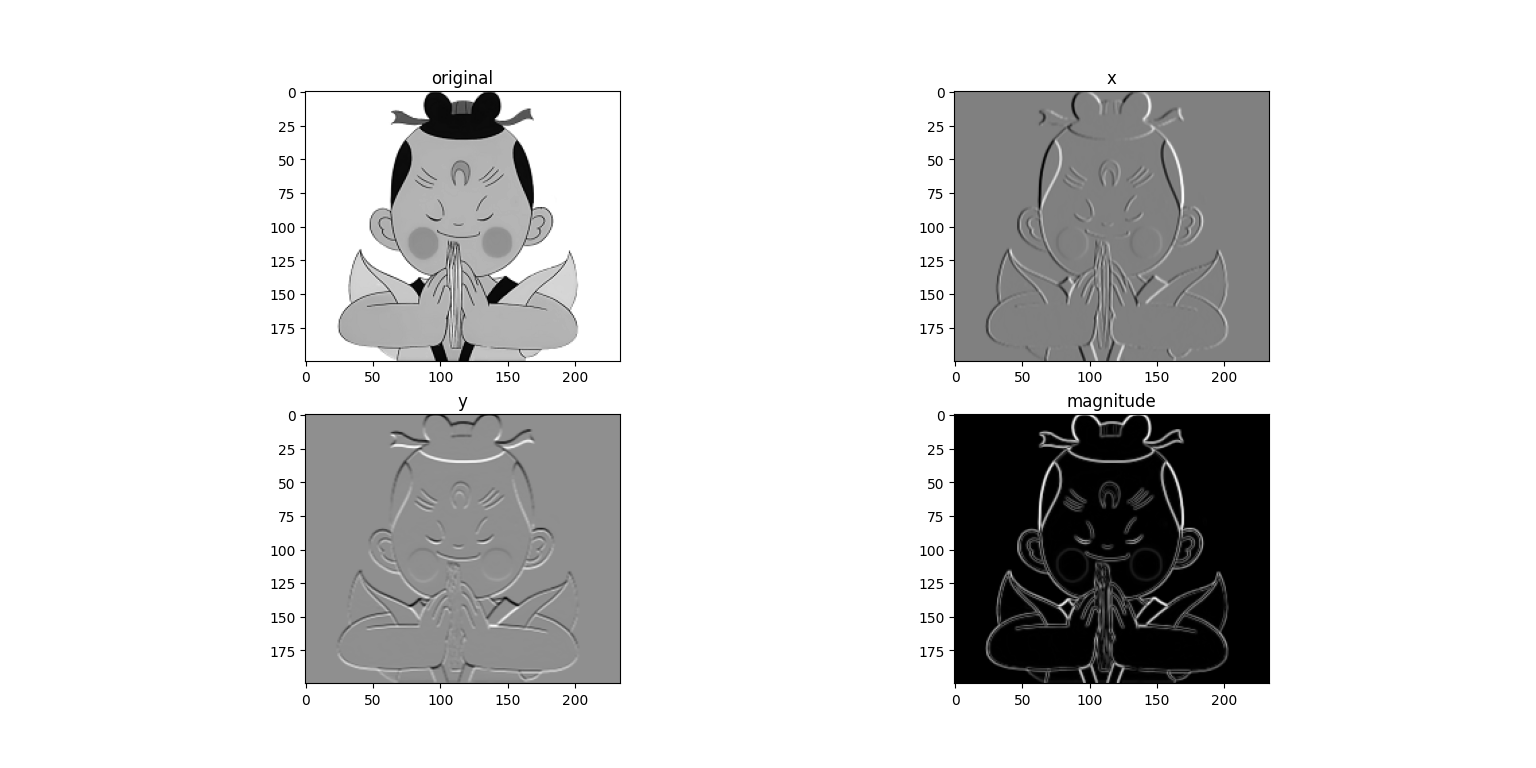
在这里插入图片描述

上图从左往右从上往下依次为原始灰度图像；x方向导数图像；y方向导数图像；梯度大小图像。在两个导数图像中，正导数显示为亮的像素，负导数显示为暗的像素。灰色区域表示导数的值接近于零。
可以看到亮的地方大多为有明显对比色差的地方。

为了在图像噪声方面更稳健，以及在任意尺度上计算导数，我们可以使用高斯导数滤波器：

       I
      
      
       x
      
     
     
      =
     
     
      
       I
      
      
       ∗
      
     
     
      
       G
      
      
       
        σ
       
       
        x
       
      
     
     
       和 
     
     
      
       I
      
      
       y
      
     
     
      =
     
     
      
       I
      
      
       ∗
      
     
     
      
       G
      
      
       
        σ
       
       
        y
       
      
     
    
    
     \boldsymbol{I}_{x}=\boldsymbol{I}^{*} G_{\sigma x} \text { 和 } \boldsymbol{I}_{y}=\boldsymbol{I}^{*} G_{\sigma y}
    
   
  Ix=I∗Gσx 和 Iy=I∗Gσy


 
  
   
    
     G
    
    
     σ
    
   
   
    x
   
  
  
   G_σx
  
 
Gσx 和

 
  
   
    
     G
    
    
     σ
    
   
   
    y
   
  
  
   G_σy
  
 
Gσy表示

 
  
   
    
     G
    
    
     σ
    
   
  
  
   G_σ
  
 
Gσ在 x 和 y 方向上的导数， 

 
  
   
    
     G
    
    
     σ
    
   
  
  
   G_σ
  
 
Gσ 为标准差为 σ 的高斯函数。

defgaussian(img, sigma):""" 
    函数功能：高斯滤波
    参数说明：img__图像
             sigma__高斯滤波参数
    函数返回：无
    """
    img_x = zeros(img.shape)
    imgx = filters.gaussian_filter(img,(sigma, sigma),(0,1), img_x)
    img_y = zeros(img.shape)
    imgy = filters.gaussian_filter(img,(sigma, sigma),(1,0), img_y)
    magnitude = sqrt(img_x **2+ img_y **2)return imgx, imgy, magnitude
 

defguassianFilter(fileName):""" 
    函数功能：高斯滤波对比
    参数说明：fileName__图像存储路径
    函数返回：无 
    """
    img_or = array(Image.open(fileName).convert('L'))
    gray()
    imgx1, imgy1, magnitude1 = gaussian(img_or,2)
    imgx2, imgy2, magnitude2 = gaussian(img_or,5)
    imgx3, imgy3, magnitude3 = gaussian(img_or,10)
    subplot(341)
    imshow(img_or), title('a'), axis('off')
    subplot(342)
    imshow(imgx1), title('b'), axis('off')
    subplot(343)
    imshow(imgx2), title('c'), axis('off')
    subplot(344)
    imshow(imgx3), title('d'), axis('off')
    subplot(345)
    imshow(img_or), title(''), axis('off')
    subplot(346)
    imshow(imgy1), title(''), axis('off')
    subplot(347)
    imshow(imgy2), title(''), axis('off')
    subplot(348)
    imshow(imgy3), title(''), axis('off')
    subplot(349)
    imshow(img_or), title(''), axis('off')
    subplot(3,4,10)
    imshow(magnitude1), title(''), axis('off')
    subplot(3,4,11)
    imshow(magnitude2), title(''), axis('off')
    subplot(3,4,12)
    imshow(magnitude3), title(''), axis('off')
    show()return

输出如下：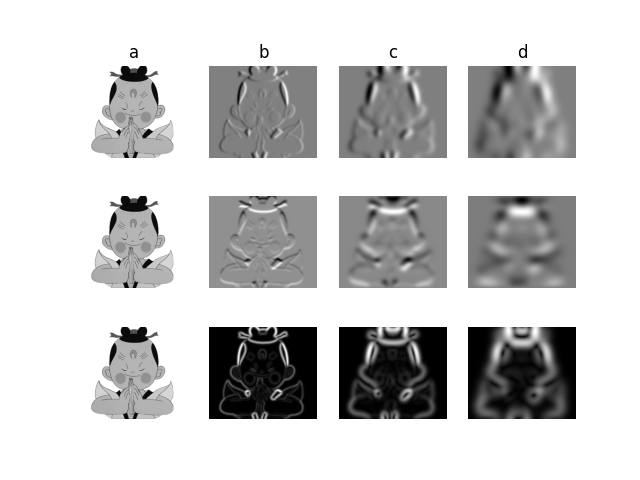
在这里插入图片描述
使用高斯导数计算图像导数： x 导数图像（上）， y 导数图像（中），以及梯度大小图像（下）；（ a）为原始灰度图像，（ b）为使用 σ=2 的高斯导数滤波器处理后的图像，（ c）为使用 σ=5 的高斯导数滤波器处理后的图像，（ d）为使用 σ=10 的高斯导数滤波器处理后的图像

形态学：对象计数

形态学（或数学形态学）是度量和分析基本形状的图像处理方法的基本框架与集合。形态学通常用于处理二值图像，但是也能够用于灰度图像。二值图像是指图像的每个像素只能取两个值，通常是 0 和 1。二值图像通常是，在计算物体的数目，或者度量其大小时，对一幅图像进行阈值化后的结果。

defbinaryImage(fileName):""" 
    函数功能：二值图像
    参数说明：fileName__图像存储路径
    函数返回：无 
    """
    img = array(Image.open(fileName).convert('L'))
    gray()
    
    subplot(221)
    imshow(img), title('original')
    img =1*(img <128)# ndimage.measurements.label(input, structure=None, output=None) # 输入一个数组，数组中非0值被认为是目标区域，0值是背景区域# 输出：label:一个被已经分好连通域的label图像：# num_feartures:统计一共有多少种连通分量的数量，例如数字5代表一共有5种，ID分别是1，2，3，4，5
    labels, nbr_objects = measurements.label(img)print("number of objects:", nbr_objects)
    
    subplot(222)
    imshow(labels), title('the picture after label')# binary_opening() 函数的第二个参数指定一个数组结构元素。该数组表示以一个像素为中心时，# 使用哪些相邻像素。在这种情况下，我们在 y 方向上使用 9 个像素（上面 4 个像素、像素本身、下面 4 个像素），# 在 x 方向上使用 5 个像素。# iterations 决定执行该操作的次数。
    img_open = morphology.binary_opening(img, ones((9,5)), iterations=2)
    
    subplot(223)
    imshow(img_open), title('open')
    labels_open, nbr_objects_open = measurements.label(img_open)print("number of objects:",nbr_objects_open)
    
    subplot(224)
    imshow(labels_open), title('result')
    show()return

输出结果如下：
在这里插入图片描述

程序识别出的连通区域有48个。

一些有用的SciPy模块

读写.mat文件

Matlab的 .mat 文件格式存储，那么可以使用 scipy.io 模块进行读取

data = scipy.io.loadmat('test.mat')

data 对象包含一个字典，字典中的键对应于保存在原始 .mat 文件中的变量名。由于这些变量是数组格式的，因此可以很方便地保存到 .mat 文件中。你仅需创建一个字典（其中要包含你想要保存的所有变量），然后使用savemat() 函数：

data ={}
data['x']= x
scipy.io.savemat('test.mat',data)

以图像形式保存数组

因为我们需要对图像进行操作，并且需要使用数组对象来做运算，所以将数组直接保存为图像文件非常有用。imsave() 函数可以从 scipy.misc 模块中载入。要将数组 im 保存到文件中，可以使用
下面的命令：

from scipy.misc import imsave
imsave('test.jpg',im)

#该脚本返回一个 512× 512 的灰度图像数组。
lena = scipy.misc.lena()

1.5　高级示例：图像去噪

图像去噪是在去除图像噪声的同时，尽可能地保留图像细节和结构的处理技术。我们这里使用 ROF（ Rudin-Osher-Fatemi）去噪模型。ROF 模型具有很好的性质：使处理后的图像更平滑，同时保持图像边缘和结构信息。

ROF模型

一幅（灰度）图像

    I
   
  
  
   I
  
 
I的全变差（Total Variation，TV）定义为梯度范数之和。在连续表示的情况下，全变差表示为：
  
   
    
     
      J
     
     
      (
     
     
      I
     
     
      )
     
     
      =
     
     
      ∫
     
     
      ∣
     
     
      ∇
     
     
      I
     
     
      ∣
     
     
      d
     
     
      x
     
    
    
     J(\boldsymbol{I})=\int|\nabla \boldsymbol{I}| \mathrm{d} \mathbf{x}
    
   
  J(I)=∫∣∇I∣dx

在离散表示的情况下，全变差表示为：

      J
     
     
      (
     
     
      I
     
     
      )
     
     
      =
     
     
      
       ∑
      
      
       x
      
     
     
      ∣
     
     
      ∇
     
     
      I
     
     
      ∣
     
    
    
     J(\boldsymbol{I})=\sum_{\mathbf{x}}|\nabla \boldsymbol{I}|
    
   
  J(I)=x∑∣∇I∣

其中，上面的式子是在所有图像坐标 x=[x, y] 上取和。

在 Chambolle 提出的 ROF 模型里，目标函数为寻找降噪后的图像 U，使下式最小：

        min
       
       
        ⁡
       
      
      
       U
      
     
     
      ∥
     
     
      I
     
     
      −
     
     
      U
     
     
      
       ∥
      
      
       2
      
     
     
      +
     
     
      2
     
     
      λ
     
     
      J
     
     
      (
     
     
      U
     
     
      )
     
    
    
     \min _{U}\|\boldsymbol{I}-\boldsymbol{U}\|^{2}+2 \lambda J(\boldsymbol{U})
    
   
  Umin∥I−U∥2+2λJ(U)

其中范数||

    I
   
   
    −
   
   
    U
   
  
  
   I-U
  
 
I−U || 是去噪后图像 U 和原始图像 

 
  
   
    I
   
  
  
   I
  
 
I差异的度量。也就是说，本质上该模型使去噪后的图像像素值“平坦”变化，但是在图像区域的边缘上，允许去噪后的图像像素值“跳跃”变化。

ROF模型去噪代码实现：

defimageFilter(fileName):""" 
    函数功能：图像去噪
    参数说明：fileName__图像存储路径
    函数返回：无 
    """   

    img = array(Image.open(fileName).convert('L'))
    gray()# 添加噪声# 括号里的参数要换成和图片一样大小的。
    img = img +30*standard_normal((200,234))
    
    U, T = denoise(img, img)

    G = filters.gaussian_filter(img,5)
    subplot(131)
    imshow(img), title('original'),axis('off')
    subplot(132)
    imshow(U), title('rof'),axis('off')
    subplot(133)
    imshow(G), title('gaussian'),axis('off')
    
    show()return

输出如下：
在这里插入图片描述
对比rof滤波和告诉滤波。rof整体图像虽然也是糊的，但是他的边缘信息保留的比较突出。对比高斯滤波整个图形都是模糊的。

1.6小结

本章内容很杂，介绍图像读取、显示、局部操作、保存、滤波等等基本操作。虽然繁多但是都是最基本的操作。是我们后续进行对图片进一步处理的基础。

本章用到的代码（我使用的Python是3.8的，有需要自取）：
链接：https://pan.baidu.com/s/1SjJn4a6P7GgpvKS0uXqRhQ?pwd=jbmf
提取码：jbmf

标签： python 计算机视觉学习

本文转载自: https://blog.csdn.net/qq_35021992/article/details/126921363
版权归原作者 书生丶丶 所有，如有侵权，请联系我们删除。

《Python 计算机视觉编程》学习笔记（一）

文章目录

前言

第 1 章基本的图像操作和处理

引言

1.1 PIL： Python图像处理类库

图像读取、显示、显示对应灰度图

更改图像格式（后缀）

创建缩略图

复制和粘贴图像区域

调整尺寸和旋转

1.2 Matplotlib

绘制图像、点和线

图像轮廓和直方图

交互式标注

1.3 NumPy

图像数组表示

灰度变换

直方图均衡化

图像的主成分分析（ PCA）

1.4 SciPy

图像模糊

图像导数

形态学：对象计数

一些有用的SciPy模块

读写.mat文件

以图像形式保存数组

1.5　高级示例：图像去噪

ROF模型

1.6小结

发表评论