139. 单词拆分

139. 单词拆分

给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict，判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。

示例 1：

输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以由 "leet" 和 "code" 拼接成。

示例 2：

输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true
解释: 返回 true 因为 "applepenapple" 可以由 "apple" "pen" "apple" 拼接成。
注意，你可以重复使用字典中的单词。

示例 3：

输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
输出: false

解题思路

其实刚开始我个人是想用双指针来做这道题的，但是考虑到需要来回逐一判断单词，维护起来很麻烦，所以就使用了 动态规划（dp），为什么会想到用 dp 呢，我们知道 dp 一般用来解决 组合、子序列问题，这题是不是就是变相的组合问题了，所以使用 dp。

这里使用 Carl 哥 的动规 五部曲

1、确定dp数组（dp table）以及下标的含义：dp 长度为n+1，n为字符串s的长度，dp[i] 表示 s 的前 i 位能否被拆分为字典中的单词。

2、确定递推公式：对于dp[i]，枚举 j 从 0 到 i-1，如果 dp[j] = true 且 s[j+1,i] 在字典中出现，那么dp[i] = true。

3、dp数组如何初始化=：dp[0] = ture ,表示空串，我们认为其可以被拆分，所以dp[0]=true。

4、确定遍历顺序：正序遍历即可，没有特殊需求

5、举例推导dp数组：
我们以示例 1 为例：
输入: s = “leetcode”, wordDict = [“leet”, “code”]
输出: true
解释: 返回 true 因为 “leetcode” 可以被拆分成 “leet code”。
我们定义 dp[i] 表示 s 的前 i 位能否被拆分为字典中的单词。
我们考虑填充 dp 数组，首先dp[0 ]= true，表示空串可以被拆分。
接下来我们枚举 i 从 1 到 n，对于每个 i，我们枚举 j 从 0 到 i-1，如果 dp[j] = true 且 s[j+1,i] 在字典中出现，那么 dp[i] =t rue。

我们可以画出如下的表格来帮助理解：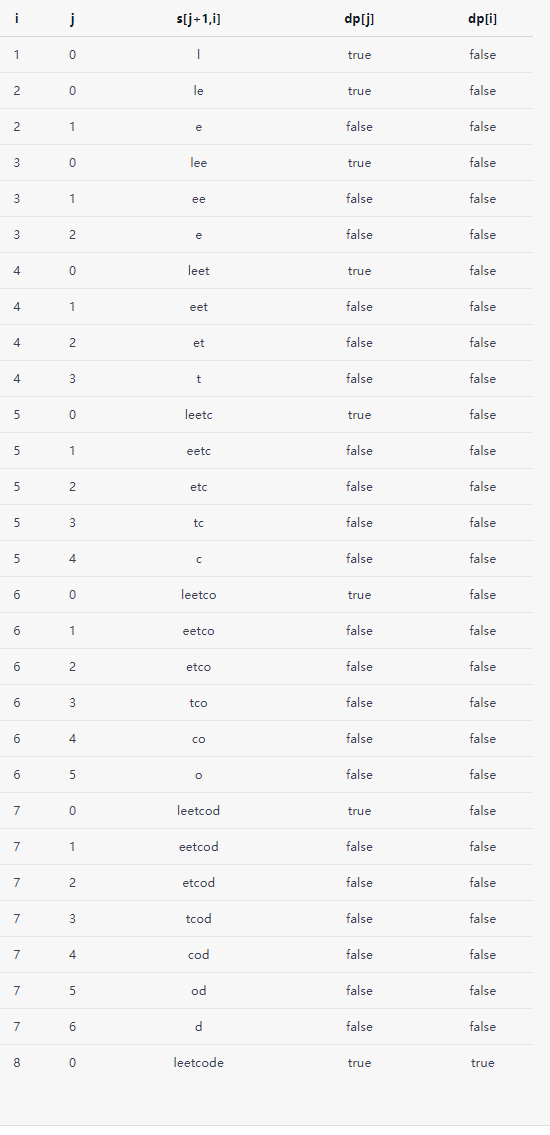

从表格中可以看出，最终dp[8]为true，所以字符串"leetcode"可以被拆分成"leet code"。

代码：

public static boolean wordBreak(String s, List<String> wordDict) {
        int n =s.length();
        boolean[] dp = new boolean[n+1]; //定义 dp 数组，长度为 n+1 ，初始化全部 false
        dp[0] = true; // 空串可以被拆分，所以dp[0]为true
        for (int i = 1; i <= n; i++) { // 枚举i从 1 到 n
            for (int j = 0; j < i; j++) { // 枚举j从0到i-1
                if (dp[j] && wordDict.contains(s.substring(j,i))){ // 如果dp[j]=true 且 s[j+1,i]在字典中出现，则说明存在
                    dp[i] = true;
                    break;
                }
            }
        }
        return dp[n];
    }