Python数据结构与算法（2.2）——顺序表

Python数据结构与算法（2.2）——顺序表

0. 学习目标

线性表在计算机中的表示可以采用多种方法，采用不同存储方法的线性表也有着不同的名称和特点。线性表有两种基本的存储结构：顺序存储结构和链式存储结构。本节将介绍顺序存储结构的特点以及各种基本运算的实现。
通过本节学习，应掌握以下内容：

• 线性表的顺序存储及实现方法
• 顺序表基本操作的实现
• 利用顺序表的基本操作实现复杂算法

1. 线性表的顺序存储结构

1.1 顺序表基本概念

线性表的顺序存储是把线性表的数据元素按逻辑次序依次存放在一组连续的存储单元中，即逻辑结构上相邻的两个数据元素存储在计算机内的物理存储位置也是相邻的，这种存储方法为整个线性表分配一整个内存块保存线性表的元素，借助数据元素在计算机内的物理位置表示线性表中数据元素之间的逻辑关系。采用顺序存储结构表示的线性表简称顺序表 (Sequential List)。
顺序表具有以下两个基本特点：

• 顺序表的所有元素所占的存储空间是连续的；
• 顺序表中各数据元素在存储空间中是按逻辑顺序依次存放的。

由于线性表的所有数据元素属于同一数据类型，所以每个元素占用的空间(字节数)相同。因此，要在此结构中查找某一个元素是很方便的，即只要知道顺序表首地址和每个数据元素在内存所占字节的大小，就可求出第

    i
   
  
  
   i
  
 
i 个数据元素的地址。通过使用特定元素的序号，可以在常数时间内访问数据元素，因此可以说顺序表具有按数据元素的序号随机存取的特点。

假设线性表中的第一个数据元素的存储地址(即顺序表第一个字节的地址，也称首地址)为

    i
   
   
    d
   
   
    (
   
   
    
     a
    
    
     1
    
   
   
    )
   
  
  
   id(a_1)
  
 
id(a1​)，每一个数据元素占 

 
  
   
    k
   
  
  
   k
  
 
k 个字节，则线性表中第 

 
  
   
    i
   
  
  
   i
  
 
i 个元素 

 
  
   
    
     a
    
    
     i
    
   
  
  
   a_i
  
 
ai​ 在计算机中的存储地址为：

 
  
   
    
     i
    
    
     d
    
    
     (
    
    
     
      a
     
     
      i
     
    
    
     )
    
    
     =
    
    
     i
    
    
     d
    
    
     (
    
    
     
      a
     
     
      1
     
    
    
     )
    
    
     +
    
    
     (
    
    
     i
    
    
     −
    
    
     1
    
    
     )
    
    
     ×
    
    
     k
    
    
        
    
    
     (
    
    
     1
    
    
     ≤
    
    
     i
    
    
     ≤
    
    
     n
    
    
     )
    
   
   
    id(a_i)= id(a_1) + (i-1) ×k\ \ \ (1≤i≤n)
   
  
 id(ai​)=id(a1​)+(i−1)×k   (1≤i≤n)

从上式可以看出，访问顺序表数据元素的过程只需要一次乘法和一次加法。由于这两个操作只需要常数时间，因此可以说顺序表访问可以在常数时间内进行。
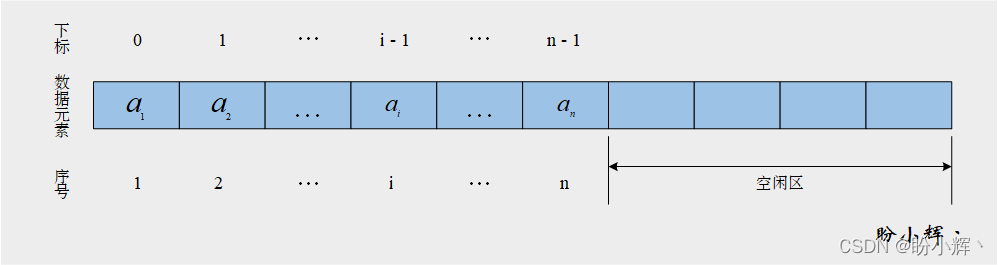
也就是说，顺序表中的每一个数据元素在计算机存储空间中的存储地址由该元素在线性表中的序号惟一确定。假设有一长度为

    n
   
  
  
   n
  
 
n 的线性表 

 
  
   
    (
   
   
    
     a
    
    
     1
    
   
   
    ，
   
   
    
     a
    
    
     2
    
   
   
    ，
   
   
    …
   
   
    ，
   
   
    
     a
    
    
     n
    
   
   
    )
   
  
  
   (a_1，a_2，…， a_n)
  
 
(a1​，a2​，…，an​)，那么其在计算机中的顺序存储结构可以用下图表示：

1.2 顺序表的优缺点

顺序表的优点：

• 简单易用
• 可以快速访问元素

顺序表的缺点：

• 固定大小：顺序表的大小是静态的(使用前需要指定顺序表大小)
• 基于位置插入元素较复杂：要在给定位置插入元素，可能需要移动现有元素来创建一个空位置，以便在所需位置插入新元素；如果要在开头添加元素，那么移位操作的开销就更大了

为了解决顺序表具有固定大小的缺陷，动态顺序表的概念被提出。

1.3 动态顺序表

动态顺序表(也称为可增长顺序表、可调整大小的顺序表、动态表)是一种随机访问、大小可变的顺序表数据结构，允许添加或删除元素，

Python

内置的

list

就是一种动态顺序表。
实现动态顺序表的一种简单方法是从一些固定大小的顺序表开始。一旦该顺序表变满，就创建高于原始顺序表大小的新顺序表；同样，如果顺序表中的元素过少，则将缩小顺序表大小。
接下来，为了更好的理解顺序表，我们将使用

Python

实现顺序表。

2. 顺序表的实现

在具体实现时，使用

Python

中的列表来对应连续的存储空间。设最多可存储

max_size

个元素，为保存线性表的长度需定义一个整型变量

num_items

。由于，

Python

列表中索引从 0 开始，因此，线性表的第

    i
   
   
    (
   
   
    1
   
   
    ≤
   
   
    i
   
   
    ≤
   
   
    n
   
   
    )
   
  
  
   i(1≤i≤n)
  
 
i(1≤i≤n) 个元素存放在列表索引为 

 
  
   
    i
   
   
    −
   
   
    1
   
  
  
   i-1
  
 
i−1 的列表元素中，为保持一致性，我们实现的顺序表的序号同样从 0 开始(也可以根据需要索引从 1 开始，只需要进行简单修改)。

2.1 顺序表的初始化

顺序表的初始化需要三部分信息：

items

列表用于存储数据元素，

max_size

用于存储

items

列表的最大长度，以及

num_items

用于记录

items

列表的当前使用的位置，即顺序表中的数据元素数量。

classSequentialList:def__init__(self, max_size=10):
        self.items =[None]* max_size
        self.num_items =0
        self.max_size = max_size

初始化代码通过创建一个包含 10 个

None

值的列表来构建一个

SequentialList

对象，内部

items

列表的初始大小

max_size

默认为 10，也可以传递更大的顺序表大小作为初始大小，该列表也可以在需要时会动态增长。创建

SequentialList

对象的时间复杂度为

    O
   
   
    (
   
   
    1
   
   
    )
   
  
  
   O(1)
  
 
O(1)。

如下图所示，是一个包含 5 个数据元素的

SequentialList

对象：

2.2 获取顺序表长度

这里所说的顺序表长度，指顺序表中数据元素的个数，由于我们在顺序表中使用

num_items

跟踪顺序表中的项数，求取顺序表长度只需要重载

__len__

从对象返回

num_items

的值，因此时间复杂度为

    O
   
   
    (
   
   
    1
   
   
    )
   
  
  
   O(1)
  
 
O(1)：

def__len__(self):return self.num_items

如果在

SequentialList

对象中没有跟踪列表的项数，那么计算顺序表长度的时间复杂度为

    O
   
   
    (
   
   
    n
   
   
    )
   
  
  
   O(n)
  
 
O(n)。

2.3 读取指定位置元素

为了实现读取顺序表指定位置元素的操作，我们将重载

__getitem__

操作，操作的复杂度为

    O
   
   
    (
   
   
    1
   
   
    )
   
  
  
   O(1)
  
 
O(1)。同时，我们希望确保索引在可接受的索引范围内，否则将像内置列表类一样引发 

IndexError

异常：

def__getitem__(self, index):if index >=0and index < self.num_items:return self.items[index]raise IndexError('SequentialList index out of range')

我们也可以实现修改指定位置元素的操作，只需要重载

__setitem__

操作，其复杂度同样为

    O
   
   
    (
   
   
    1
   
   
    )
   
  
  
   O(1)
  
 
O(1)：

def__setitem__(self, index, val):if index >=0and index < self.num_items:
            self.items[index]= val
            returnraise IndexError("SequentialList assignment index out of range")

2.4 查找指定元素

要确定值为 x 的元素在顺序表中的位置，需要依次比较各元素。当查询到第一个满足条件的数据元素时，返回其下标，否则像内置列表类一样引发

ValueError

异常，表示查找失败。

deflocate(self, item):for i inrange(self.num_items):if self.items[i]== item:return i
        raise ValueError("{} is not in sequential list".format(item))

在查找过程中，数据元素比较次数的平均值为

      n
     
     
      +
     
     
      1
     
    
    
     2
    
   
  
  
   \frac {n+1} 2
  
 
2n+1​，因此时间复杂度为 

 
  
   
    O
   
   
    (
   
   
    n
   
   
    )
   
  
  
   O(n)
  
 
O(n)。

2.5 在指定位置插入新元素

实现在指定位置插入新元素之前，我们首先看下如何在顺序表末尾追加元素。追加时，如果有空闲空间，只需要在

self.items

列表的末尾再添加一项，而当

self.items

列表填满时，我们必须增加

self.items

列表的大小，为需要追加的新元素创建空间，创建的新

self.items

大小与

self.items

的当前长度成正比。
为了使追加操作在

    O
   
   
    (
   
   
    1
   
   
    )
   
  
  
   O(1)
  
 
O(1) 时间内运行，我们不能在每次需要更多空间时仅增加一个空闲位置，事实证明，每次增加 

25%

的空间就足以保证

    O
   
   
    (
   
   
    1
   
   
    )
   
  
  
   O(1)
  
 
O(1) 复杂度。选择增加空间的百分比并不重要，每次增加 10% 或100%的空间，同样可以使时间复杂度为 

 
  
   
    O
   
   
    (
   
   
    1
   
   
    )
   
  
  
   O(1)
  
 
O(1)。这里选择 25% 的原因是可以在不占用太多计算机内存的情况下多次使用追加操作扩展列表。

def__alloc(self):
        new_size =(self.max_size //4)+ self.max_size +1
        new_items =[None]* new_size
        for i inrange(self.num_items):
            new_items[i]= self.items[i]
        
        self.items = new_items
        self.max_size = new_size

    defappend(self, item):if self.num_items == self.max_size:
            self.__alloc()
        
        self.items[self.num_items]= item
        self.num_items +=1

要插入新数据元素到顺序表中，必须为新元素腾出空间，下图表示顺序表中的列表在进行插入操作前后，其数据元素在列表中下标的变化情况：

完成如上的插入操作要经过如下步骤：

1. 线性表中指定位置及其之后的元素，依次向后移动一个位置，空出索引为 i i i 的位置
2. 数据元素 x 插入到第 i i i 个存储位置
3. 插入结束后使线性表的长度增加 1

需要注意的是，如果线性表空间已满，首先需要分配新的空间。如果提供的索引大于列表的大小，则将新项 x 附加到列表的末尾。插入时间元素操作的时间复杂度为

    O
   
   
    (
   
   
    n
   
   
    )
   
  
  
   O(n)
  
 
O(n)。

definsert(self, index, item):if self.num_items == self.max_size:
            self.__alloc()if index < self.num_items and index >=0:for j inrange(self.num_items-1, index-1,-1):
                self.items[j+1]= self.items[j]
            self.items[index]= item
            self.num_items +=1elif index >= self.num_items:
            self.append(item)else:raise IndexError("SequentialList assignment index out of range")

2.6 删除指定位置元素

当删除列表中特定索引处的数据元素时，我们必须将其之后的所有元素向下移动以保证内部列表中没有无效数据。下图表示一个顺序表在进行删除运算前后，其数据元素下标的变化：

在线性表上完成上述操作需要以下步骤：

1. 在线性表中删除下标为i的元素，从索引为 i + 1 i+1 i+1 到 n − 1 n-1 n−1 的元素依次向前移动依次向前移动一个位置，将所删除的索引为 i i i 的数据元素 a i + 1 a_{i+1} ai+1​ 覆盖掉，从而保证逻辑上相邻的元素物理位置也相邻
2. 修改顺序表长度，使其减 1

为了实现删除顺序表指定位置元素的操作，我们将重载

__getitem__

操作，在顺序表上删除数据元素时大约需要移动表中一半的元素，显然该算法的时间复杂度为

    Ｏ
   
   
    (
   
   
    n
   
   
    )
   
  
  
   Ｏ(n)
  
 
Ｏ(n)。

def__delitem__(self, index):for i inrange(index, self.num_items-1):
            self.items[i]= self.items[i+1]
        self.num_items -=1

2.7 其它一些有用的操作

为了更好的使用顺序表，接下来将介绍其它一些很有用的操作。
例如，将顺序表转换为字符串以便进行打印，使用

str

函数调用对象上的

__str__

方法可以创建适合打印的字符串表示，

__str__

的返回结果的可读性很强：

def__str__(self):
        s ='['for i inrange(self.num_items):
            s +=repr(self.items[i])if i < self.num_items -1:
                s +=', '
        s +=']'return s

我们也可以重载成员资格函数

__contain__

来检查一个数据元素是否是顺序表中的元素之一。这样做的唯一方法是按顺序检查顺序表中的每个数据元素。如果找到该项目，则返回

True

，否则返回

False

这种搜索方法称为线性搜索，之所以这样命名是因为它具有

    O
   
   
    (
   
   
    n
   
   
    )
   
  
  
   O(n)
  
 
O(n) 的时间复杂度：

def__contains__(self, item):for i inrange(self.num_items):if self.items[i]== item:returnTruereturnFalse

检查两个顺序表的相等性首先需要两个顺序表的类型相同以及两个顺序表必须具有相同的长度。在满足这两个先决条件的情况下，如果两个表中的所有元素都相等，则我们可以说两个顺序表相等，相等测试的时间复杂度为

    O
   
   
    (
   
   
    n
   
   
    )
   
  
  
   O(n)
  
 
O(n)，我们重载 

__eq__

方法实现此操作：

def__eq__(self, another):iftype(another)!=type(self)or self.num_items != another.num_items:returnFalsefor i inrange(self.num_items):if self.items[i]!= another.items[i]:returnFalsereturnTrue

3. 顺序表应用

接下来，我们首先对上述实现的顺序表进行测试，以验证操作的有效性，然后利用实现的基本操作来实现更复杂的算法。

3.1 顺序表应用示例

首先初始化一个顺序表 sample_sqlist，并在其中追加若干元素：

sample_sqlist = SequentialList()
sample_sqlist.append(11)
sample_sqlist.append(22)
sample_sqlist.append(33)

我们可以直接打印顺序表中的数据元素、顺序表长度等信息：

print('顺序表数据元素为：', sample_sqlist)print('顺序表长度：',len(sample_sqlist))print('顺序表中第0个数据元素：', sample_sqlist[0])# 修改数据元素
sample_sqlist[1]=2022print('顺序表数据元素为：', sample_sqlist)

以上代码输出如下：

顺序表数据元素为： [11, 22, 33]
顺序表长度： 3
顺序表中第0个数据元素： 11
顺序表数据元素为： [11, 2022, 33]

接下来，我们将演示在指定位置添加/删除元素、以及如何查找指定元素等：

print('在顺序表位置1处添加元素2021')
sample_sqlist.insert(1,2021)print('添加元素后，顺序表数据元素为：', sample_sqlist)print('删除顺序表位置2处元素')del(sample_sqlist[2])print('删除数据后，顺序表数据元素为：', sample_sqlist)print('元素11的索引为{}'.format(sample_sqlist.locate(11)))print('11在顺序表中?',11in sample_sqlist)print('22在顺序表中?',22in sample_sqlist)

以上代码输出如下：

在顺序表位置1处添加元素2021
添加元素后，顺序表数据元素为： [11, 2021, 2022, 33]
删除顺序表位置2处元素
删除数据后，顺序表数据元素为： [11, 2021, 33]
元素11的索引为0
11在顺序表中? True
22在顺序表中? False

3.2 利用顺序表基本操作实现复杂操作

[1] 利用顺序表的基本操作，合并两个顺序表：

defadd_sqlist(sqlist1, sqlist2):
    result = SequentialList(max_size=sqlist1.num_items+sqlist2.num_items)for i inrange(sqlist1.num_items):
        result.append(sqlist1[i])for i inrange(sqlist2.num_items):
        result.append(sqlist2[i])return result
# 算法测试
sqlist1 = SequentialList()
sqlist2 = SequentialList()for i inrange(10):
    sqlist1.append(i)
    sqlist2.append(i*5)print('顺序表1：', sqlist1,'顺序表2：', sqlist2)# 合并顺序表
result = add_sqlist(sqlist1, sqlist2)print('合并顺序表：', result)

可以看到合并两个顺序表的时间复杂度为

    O
   
   
    (
   
   
    n
   
   
    )
   
  
  
   O(n)
  
 
O(n)，程序输出结果如下：

顺序表1： [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] 顺序表2： [0, 5, 10, 15, 20, 25, 30, 35, 40, 45]
合并顺序表： [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 5, 10, 15, 20, 25, 30, 35, 40, 45]

[2] 利用顺序表 sqlist1 和 sqlist2 中公共数据元素生成新顺序表：

defcommelem(sqlist1, sqlist2):
    result = SequentialList()for i inrange(sqlist1.num_items):if sqlist1[i]in sqlist2 and sqlist1[i]notin result:
            result.append(sqlist1[i])return result
# 算法测试
sqlist1 = SequentialList()
sqlist2 = SequentialList()for i inrange(5):
    sqlist1.append(i*2)
    sqlist1.append(i)
    sqlist2.append(i*3)print('顺序表1：', sqlist1,'顺序表2：', sqlist2)# 合并顺序表
result = commelem(sqlist1, sqlist2)print('两顺序表中的公共元素：', result)

可以看到算法的时间复杂度为

    O
   
   
    (
   
   
    
     n
    
    
     2
    
   
   
    )
   
  
  
   O(n^2)
  
 
O(n2)，程序输出结果如下：

合并顺序表： [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 5, 10, 15, 20, 25, 30, 35, 40, 45]
顺序表1： [0, 0, 2, 1, 4, 2, 6, 3, 8, 4] 顺序表2： [0, 3, 6, 9, 12]
两顺序表中的公共元素： [0, 6, 3]

相关链接

线性表基本概念