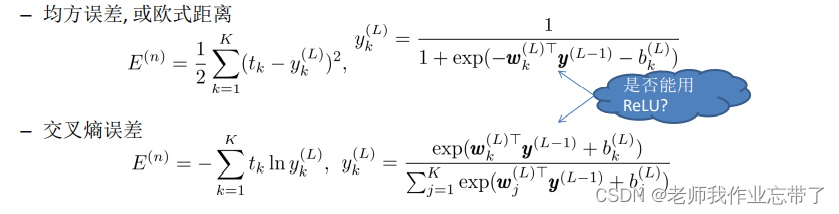AI遮天传 DL-多层感知机

本文介绍多层感知机，会先按照历史顺序介绍多层感知机诞生前的一些模型，后面介绍具体实现与其算法。

一、前戏

1.1 阈值逻辑单元(Threshold Logic Unit, TLU)

如上图是一个神经元，我们可以看到它的胞体、轴突、树突。

我们高中的时候学过一种东西叫做神经递质，分为抑制性神经递质和兴奋性神经递质，以及一些关于兴奋和抑制相关的知识；

我们把这些递质看作神经元的输入，则可模仿神经元建立以下模型(M-P unit)：

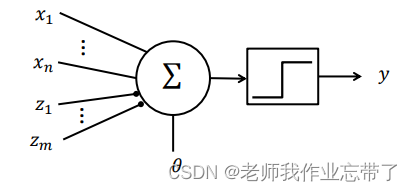
其中：

那个方块中的符号代表阶跃函数

$x_{i}$ 兴奋性输入

$z_{i}$ 抑制性输入

$y_{i}$ 二元化输出

输入与输出都是二进制的

$\theta$ 阈值

解释如下：

M-P单元可以被单个抑制性信号所抑制，就像真实的神经元一样。
如果 $z_{1}$ , $z_{2}$ , . . . , $z_{m}$ 至少有一个为 1, 则该单元被抑制且 𝑦 = 0
否则将计算总激活值 $T = \sum_{i=1}^{n}x_{i}$ 并与阈值 𝜃 相比较 (如果𝑛 = 0 则 𝑥 = 0) - 如果𝑇 ≥ 𝜃 则发放值为1，表示兴奋。- 如果𝑇 < 𝜃 结果为0，表示非兴奋。

我们还可以用该模型实现布尔函数：

比如一组数据 0 0 1 0，合取为0，析取为1，我们只需分别把阈值设置为4和1即可：

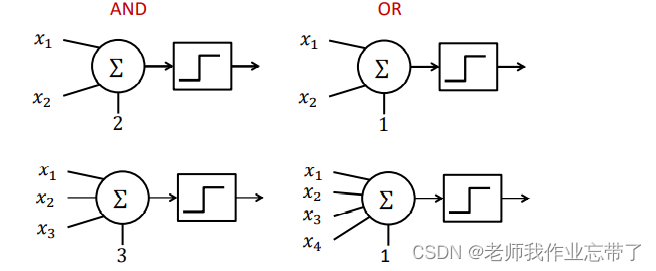
这样加和做非线性处理后与阈值进行比较即可得到想要的答案。

当然若是想实现取反操作，则可以加上抑制性输入或使用非门。

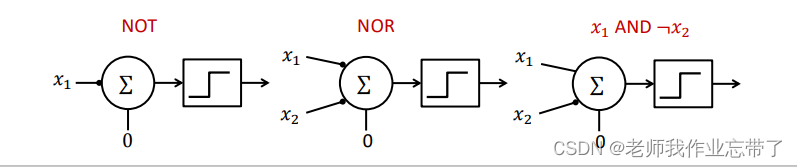
单调逻辑函数

单调逻辑函数： 𝑓 指的是对于给定的两组n元逻辑变量 𝒙 = (𝑥1, … , 𝑥𝑛) 和 𝒚 = (𝑦1, … , 𝑦𝑛), 当输入𝒚 中的1是输入 𝒙 的子集时，满足𝑓 𝒙 ≥ 𝑓(𝒚).

上面定义看不懂没关系，这里举个例子：x=(0,1,1,0), y=(0,0,1,0)；则x构成集合{ $1_{1}$ , $1_{2}$ }, y构成集合{ $1_{1}$ } 集合2里只有1个1，集合1里有两个，集合2是集合1的子集，那就是单调的。

命题1：不受限制的McCulloch–Pitts(M-P)单元只能实现单调逻辑函数。

即我们前面学的 and 和 or 都是单调逻辑函数，而 not nor等需要引入抑制，不是单调逻辑函数。

结构性综合(Constructive Synthesis)

每个具有n元变量的逻辑函数都可以被写成列表形式。

假设有K行的结果是1: - 用一个M-P单元来表示结果是1的n元变量- 用析取操作来连接K个M-P单元

例如, 当 𝑛 = 3 时：

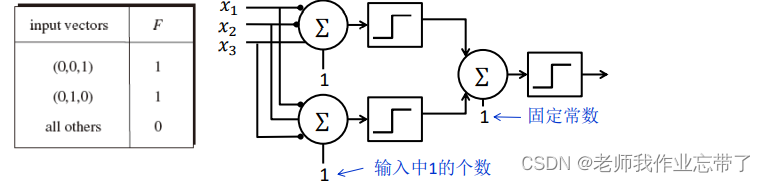
比如我们自己定义一个逻辑函数：只有输入为(0,0,1) (0,1,0) 时输出结果为1，其它都为0。

则对每一组数据的x1,x2,x3执行右侧操作:

第一行专门为(0,0,1)设置，第二行专门为(0,1,0)设置。
对于一组数据，如果是(0,0,1)或者(0,1,0)其中一个，即经过第一行和第二行计算输出结果为1和0，经过一二行析取(析取的阈值肯定是1，前面的阈值要看我们自己怎么定义)，得到结果为1。
如果输入不在这两种情况里面，则第一层的一二行返回都是0，析取为0。
如果x1为1，则该单元被抑制，直接输出y=0。

命题2：任何逻辑函数 𝐹 ∶ $\begin{Bmatrix} 0,1 \end{Bmatrix}^{n}$ → {0, 1} 都能由一个两层的M-P网络计算得到。

注：这里两层指的是左右两层，第一层上下可以是多行。

什么是构造所有逻辑函数的基本单元?

我们前面所学，抑制性连接可以被非门代替；

对于一个输入：(0,0,1)为1，其它为0：

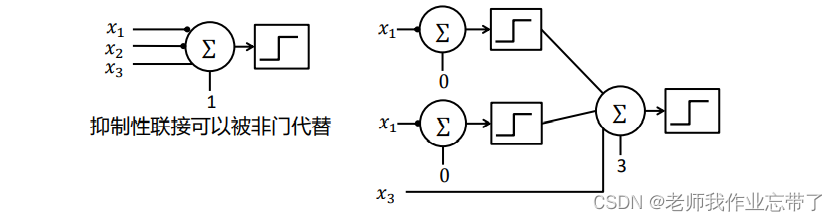
则此时x1，x2是抑制性连接，可以写成非的形式。

左侧x1，x2，x3求和为1，且此时抑制单元x1，x2都为0，输出1(析取)，否则0.
右侧如果x1为0输出1，x2为0输出1，与x3求和为3，与阈值3比较，输出1(合取)，否则0.

即右侧写法与左侧输出相同。

命题3：所有的逻辑函数都能被包含与、或、非功能的网络所实现。

命题1：不受限制的McCulloch–Pitts(M-P)单元只能实现单调逻辑函数。

命题2：任何逻辑函数 𝐹 ∶ $\begin{Bmatrix} 0,1 \end{Bmatrix}^{n}$ → {0, 1} 都能由一个两层的M-P网络计算得到。

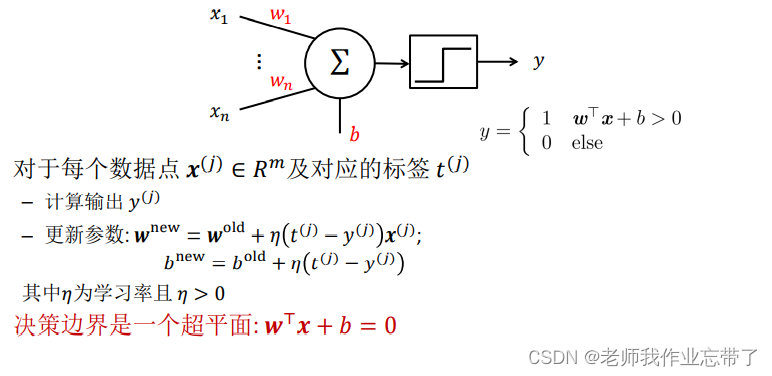
1.2 感知机 (Perceptron)

之前我们输入的都是逻辑单元01，这次x可以为实数，对x进行加权(w)，求和，与阈值(b)进行比较，同样大于的取1，不大于的取0或者-1。

这个比较操作通过移项可以写成公式 $\large w^{T}x+b > 0$ ，w和x为行或列数为1的矩阵，相乘结果为实数。

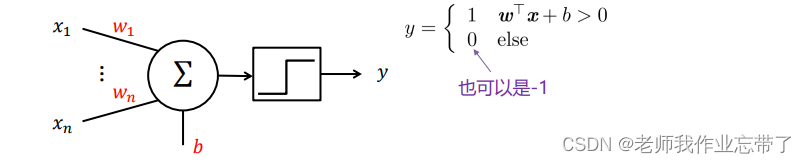
在M-P单元的输入连接上加上权重

提出监督学习:

对于每个数据点 $x^{(j)}\epsilon R^{m}$ 及对应的标签 $t^{(j)}$ , 计算输出 $y^{(j)}$

更新参数: $w^{new} = w^{old}+\eta (t^{(j)}-y^{(j)})x^{(j)}$ ; $b^{new} = b^{old}+\eta (t^{(j)}-y^{(j)})$

决策表边界是一个超平面 $w^{T}+b=0$

其中𝜂为学习率且 𝜂 > 0

注：该更新参数的过程类似于梯度下降，不过对于t和y它们是离散的，但在有限距离内依旧可以收敛但正确解上：

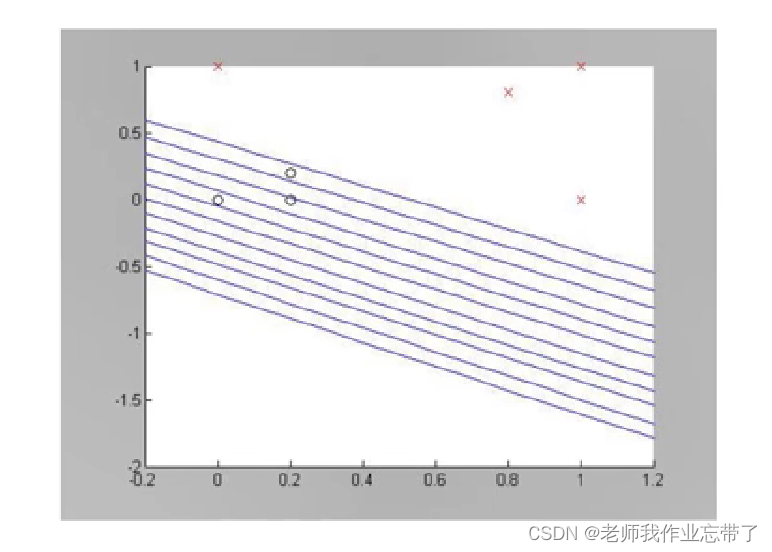
命题 4: 如果训练数据集线性可分，则感知机必定能收敛。并且训练中需要迭代的次数存在一个上限。证明参见 (Novikoff, 1962)

命题1：不受限制的McCulloch–Pitts(M-P)单元只能实现单调逻辑函数。

命题2：任何逻辑函数 𝐹 ∶ $\begin{Bmatrix} 0,1 \end{Bmatrix}^{n}$ → {0, 1} 都能由一个两层的M-P网络计算得到。

命题3：所有的逻辑函数都能被包含与、或、非功能的网络所实现。

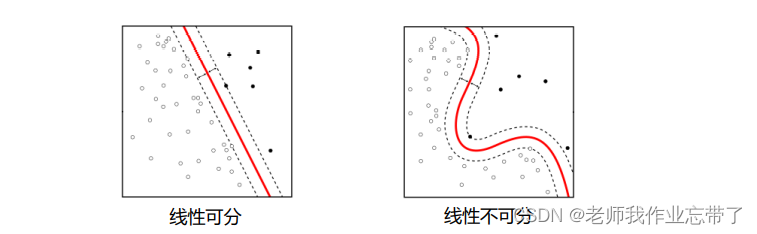
缺点: 决策边界通常与样本点距离很近, 因此对噪声敏感。

对于图右侧，无法寻找一个线性超平面将其分解，这也使得神经网络进入第一次低潮。

同一层内的多个感知机

当多个感知机被组合起来时, 输出神经元之间是互相独立的; 因此多个感知机的学习过程可以看成是相互独立的。

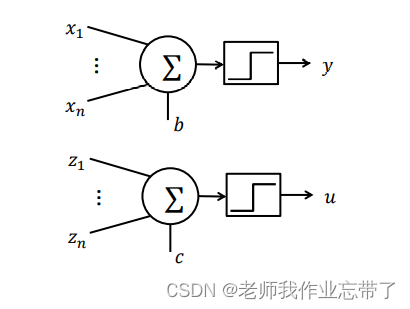
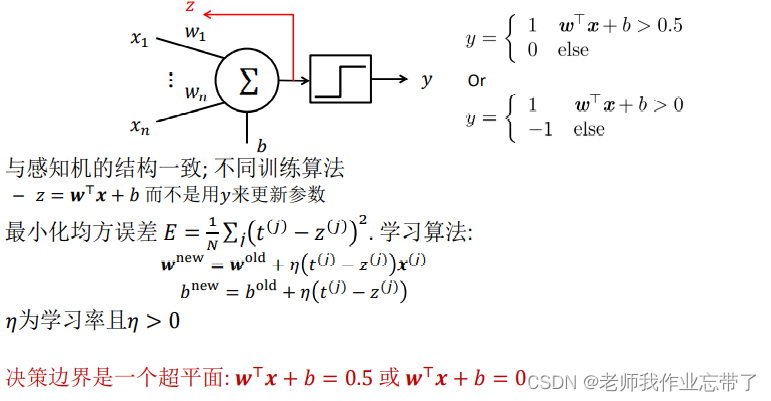
1.3 自适应线性神经网络(ADALINE)和MADALINE模型

结构与感知机一致，训练算法不同。

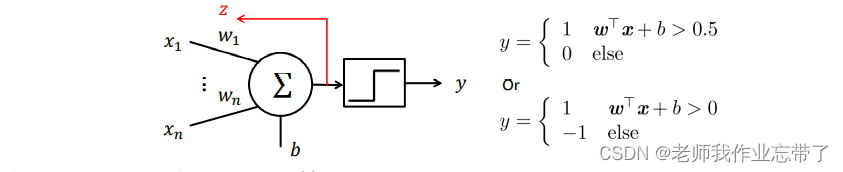
用 $z = w^{T}x+b$ 而不是用𝑦来更新参数

最小化均方误差 $E = \frac{1}{N}\sum_{j=1}^{n}(t^{(j)}-z^{(j)})^{2}$ .

学习算法: $w^{new} = w^{old}+\eta (t^{(j)}-z^{(j)})x^{(j)}$ , $b^{new} = b^{old}+\eta (t^{(j)}-z^{(j)})$

决策表边界是一个超平面 $w^{T}+b=0$ 或 $w^{T}+b=0.5$

𝜂为学习率且𝜂 > 0

别名: LMS规则，Delta规则，Widrow-Hoff 规则，实际上是SGD。

另一视角：

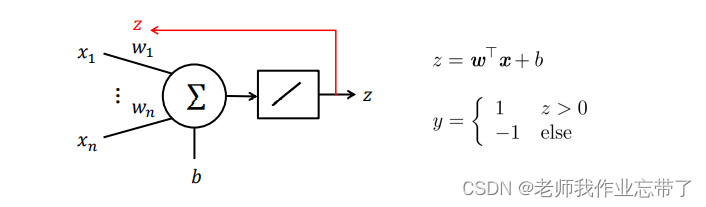
对变量 𝑧 的线性激活函数 (这也是名字中(Adaptive Linear Neuron)线性的由来)
阶跃函数只作用于输出𝑦 并且输出不参与学习过程

MADALINE模型

MADALINE: 多个ADALINE模型。
用于分类的三层(输入层, 隐含层, 输出层)全连接前馈网络，将 ADALINE作为其隐含层和输出层单元。
三种不同的MADALINE训练算法: - 最早追溯到1962年并且不能用于更新隐含层和输出层的连接权重。- 1988年提出了改进训练算法。- 第三个算法应用于改进后的网络，将阶跃函数替换成 sigmoid激活函数; 后来被证明与反向传播等价。

二、多层感知机

2.1 回顾：

感知机：

自适应线性神经网络(ADALINE)

用ADALINE解决异或(XOR)问题:

布尔函数：
$x_{1}$ $x_{2}$ t000011101110
误差函数: $E = \frac{1}{4}\sum_{j=1}^{4}(t^{(j)}-z^{(j)})^2$ 其中 $z^{(j)}=w^{T}x^{(j)}+b$

令 𝛻𝒘𝐸 = 0, 𝛻𝑏𝐸 = 0, 则

$2w_{1}+2w_{2}+4b=2$

$2w_{1}+w_{2}+2b=1$

$w_{1}+2w_{2}+2b=1$

则求得： $w = (0,0)^{T}\: \: b=0.5$

这样的话无论输入什么，输出都成了定值0.5，显然是错的。

在二维平面上显然无法有一条直线将0和1分开。

局限：

感知机和ADALINE都只能解决线性可分的分类问题
这个问题导致了神经网络领域的研究在1960-1970年代退潮 (第一次寒冬)
如果所研究的问题是线性不可分的，我们该怎么做?

这个问题主要是由于它是一个单层模型，这个时候我们就要用到多层感知机，对输入进行一个非线性的转换，转换到另外的一个空间，我们称作特征空间，经过多次转换有可能在一个特征空间就可以用一个超平面把这几个点给分开了。

此外在SVM领域核函数向量机(Kernel SVM)专门用来解决这种情况。

2.2 多层感知机(Multi-layer Perceptron, MLP)

以下是一个多层感知机的结构，每个计算单元我们用圆圈来表示。

对于输入来讲x就是问题的一种表示，对于图像来讲的话那么x就是一个像素点(一个实数来表示灰度、一个三维向量表示RGB值)，对于声音来讲的话x为每刻声音的强度，对于自然语言的话x表示每个单词...

其他层都要做计算，包括输出层，像之前所介绍的Softmax输出一个y值，与标签t进行比较。中间还有很多层，叫做隐藏层。

隐藏层的目的就是要对输入进行多次的非线性变换，期望经过多次的变换，输出能够用一个很简单的模型，比如线性回归的模型就能把类别分开。

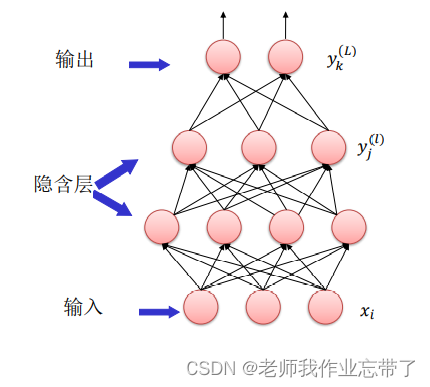
除了输入共 𝐿 层

连接类型:

相邻层之间的神经元两两连接(多层感知机又叫全连接模型)

相邻层之间没有反馈连接(单项箭头)

同一层内没有横向连接

每个神经元接收前一层神经元的输出，并根据激活函数作出响应。

前向传播

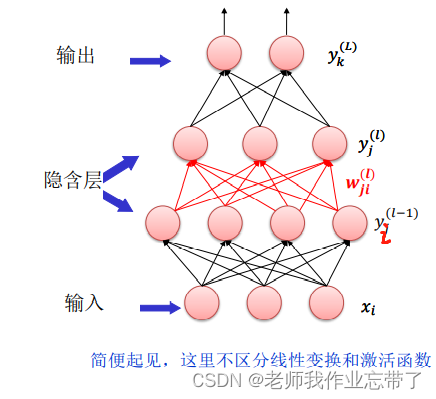
遍历 𝑙 = 1, … , 𝐿 − 1。
计算第 𝑙 层的神经元 𝑗 的输入 $z_{j}^{(l)} = \sum_{i}^{} w_{ji}^{(l)} y_{i}^{(l-1)} +b_{j}^{(l)}$ 及其输出 $y_{j}^{(l)}=f(z_{j}^{(l)})$ 。
$w_{ji}$ 表示l层单元 j 与l-1层单元 i 之间的权重， $b_{j}$ 表示整个l -1 层与 l 层单元 j 的偏置。
𝑓 是激活函数，注意 $y^{(0)}=x$ 即第一层输入。
𝑙 = 𝐿 即最后一层对应分类层，比如回归。

比如对于第l层每一个单元，它的数值yj由：

前l-1层全部数据的加权求和再加上一个偏置得到u。
对z进行y=f(z)激活得来。

对于偏置：也可以把偏置看作每一层多出来一个神经元，这样就可以把它吸收到w里面去进行公式化简。

向量形式的前向计算

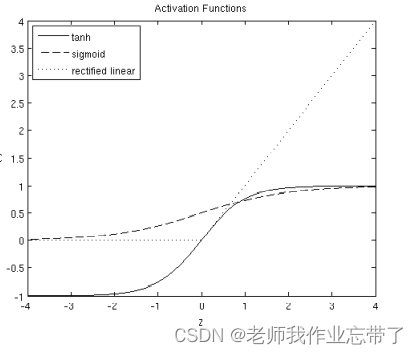
激活函数

Logistic函数及其梯度

$f(z) = \frac{1}{1+exp(-z)}$

$f(z)^{'} = f(z)(1-f(z))$

双曲正切函数及其梯度

$f(z)=tanh(z)=\frac{e^{z}-e^{-z}}{e^{z}+e^{-z}}$

$f(z)^{'}=1-f(z)^2$

整流线性激活函数(ReLU)及其梯度

$f(z) = max(0,z)$

$f(z)^{'} = \left\{\begin{matrix} 1 & z\geq 0\\ 0 & else \end{matrix}\right.$

再看异或(XOR)问题

布尔函数：
$x_{1}$ $x_{2}$ t000011101110
我们从多层感知机的角度考虑上述问题：

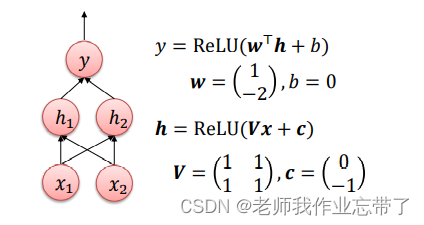
我们在输入层与输出层之间加入了一个隐藏层，权值为V，偏置为c。

则经过这一层，分别对于上表4种情况的h为： $(0,0)^{T},(1,0)^{T},(1,0)^{T},(2,1)^{T}$

ps: $(0,-1)^{T},(1,0)^{T},(1,0)^{T},(2,1)^{T}$ 取ReLU结果为： $(0,0)^{T},(1,0)^{T},(1,0)^{T},(2,1)^{T}$

此时就变得线性可分了。

继续计算得到y，分别为0，1，1，0与 t 一一对应，相同。

这样XOR问题就可以被正确求解，但该问题比较简单，我们可以通过试一试的办法把权值和偏置试出来，但对于一个实际问题，维数很高，我们就需要让机器去学习这些算法。

2.3 反向计算

我们在反向计算中就会使用BP算法来学习这些参数。

我们回顾多层感知机，其倒数第二层会把问题引入到如分类问题上去，

损失函数: $E = \frac{1}{N}\sum_{n=1}^{N}E^{(n)}$

其中 $E^{(n)}$ 是每个样本n的损失函数

以上y分别使用了 logistic/sigmoid 函数和 softmax 函数

如果是均方误差或欧氏距离，可以使用ReLU其它的如双曲正切。

而使用交叉熵函数作为损失函数，不能用ReLU。

输出层的激活函数和损失函数由任务类型决定，见下表。它们与隐藏层的激活函数的选择是独立的。

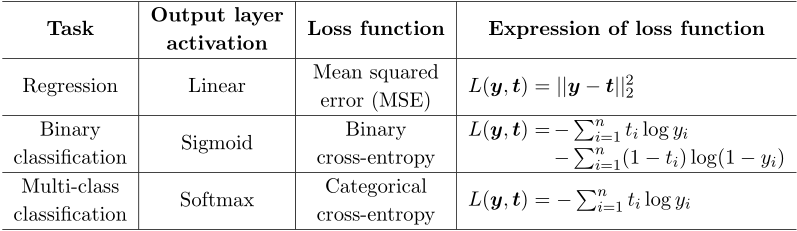
参数更新

参数更新(α为学习率)

$w_{ji}^{(l)} = w_{ji}^{(l)}-\alpha \frac{\partial E}{\partial w_{ji}^{(l)}}$ $b_{j}^{(l)} = b_{j}^{(l)}-\alpha \frac{\partial E}{\partial b_{j}^{(l)}}$

正则化(在损失函数加上额外的一项，叫做权重衰减，减轻过拟合。)

$J = E + \frac{\lambda }{2}\sum_{i,j,l}^{}(w_{ji}^{(l)})^{2}$

参数衰减通常作用于 $w_{ji}^{(l)}$ (对 $b_{j}^{(l)}$ 不必要，只有w与x相乘)

𝑤的参数更新变为:

$w_{ji}^{(l)} = w_{ji}^{(l)}-\alpha \frac{\partial J}{\partial w_{ji}^{(l)}} = w_{ji}^{(l)}-\alpha \frac{\partial E}{\partial w_{ji}^{(l)}}-\alpha \lambda w_{ji}^{(l)}$

梯度、局部敏感度

定义局部敏感度： $\delta _{i}^{(l)} = \frac{\partial E^{(n)}}{\partial u_{i}^{(l)}}$

对于 $1\leq l\leq L$ :

$\frac{\partial E^{(n)}}{\partial w_{ji}^{(l)}} = \delta _{j}^{(l)}\frac{\partial u_{j}^{(l)}}{\partial w_{ji}^{(l)}} = \delta _{j}^{(l)}f(u_{i}^{(l-1)})$

$\frac{\partial E^{(n)}}{\partial b_{j}^{(l)}} = \delta _{j}^{(l)}$

其中 $u_{j}^{(l)} = \sum_{i}^{}w_{ji}^{(l)}f(u_{i}^{(l-1)})+b_{j}^{(l)}$ f 是激活函数。

即我们求误差函数对所有参数的偏导，等价去于计算各层的局部敏感度。

局部敏感度求法

从最后一层出发，最后一层损失函数可能是 MSE 或者 Softmax交叉熵层。

均方误差(MSE)层的局部敏感度

Softmax交叉熵层的局部敏感度

其它层的局部敏感度

向量形式的反向传播

梯度消失(Gradient Vanishing)

对于隐含层 1 ≤ 𝑙 < 𝐿:

$\delta ^{(l)}=(W^{(l+1)})^{T}\delta ^{(l+1)}\odot f^{'}(u^{(l)})$

对于logistic函数

$f(z)=\frac{1}{1+exp(-z)}$

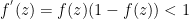
    则 ![f^{'}(z)=f(z)(1-f(z))<1](https://latex.codecogs.com/gif.latex?%5Cdpi%7B100%7D%20f%5E%7B%27%7D%28z%29%3Df%28z%29%281-f%28z%29%29%3C1)

对于tanh函数

$f(z)=tanh(z)=\frac{e^{z}-e^{-z}}{e^{z}+e^{-z}}$

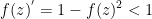
    则 ![f(z)^{'}=1-f(z)^2<1](https://latex.codecogs.com/gif.latex?%5Cdpi%7B100%7D%20f%28z%29%5E%7B%27%7D%3D1-f%28z%29%5E2%3C1)

对于这两个激活函数, 从第𝐿层到第一层, 𝜹 (𝑙) 变得越来越小。浅层的梯度会逐渐接近于零。

$\frac{\partial E^{(n)}}{\partial W^{(l)}} = \delta ^{(l)}(f(u^{(l-1)}))^{T},\, \frac{\partial E^{(n)}}{\partial b^{(l)}} = \delta ^{(l)}$

ReLU可以缓解这一问题

实现过程

前向计算 – 计算 $f(u^{(l)})$ 和 $f^{'}(u^{(l)})$ , 对所有的 𝑙 = 1,2, … , 𝐿

后向计算 – 计算 $\delta ^{(l)}$ 和 $\frac{\partial E}{\partial w^{(l)}},\frac{\partial E}{\partial b^{(l)}}$ 对所有的 𝑙 = 𝐿, 𝐿 − 1, … ,1

对所有 𝑙 = 1,2, … , 𝐿, 更新 $w^{(l)}$ 和 $b^{(l)}$

模块化编程

用类来实现层，并提供前向和后向计算函数。
不同类型的层拥有不同的前向和后向计算函数，例如输入层、隐含层、softmax输出层、sigmoid输出层等。
通过组合不同的模块来构造不同的多层感知机模型。

实验

实验1：对二维平面上的点进行分类

A Neural Network Playground (tensorflow.org)

实验2: 手写体数字识别

ConvNetJS MNIST demo (stanford.edu)

2.4 层分解

输入层或隐含层

$y_{j}^{(l)} = f(\sum_{i}^{} w_{ji}^{(l)} y_{i}^{(l-1)} +b_{j}^{(l)})$

可以被解构为两层

全连接层： $u_{j}^{(l)} = \sum_{i}^{} w_{ji}^{(l)} y_{i}^{(l-1)} +b_{j}^{(l)}$

激活层： $y_{j}^{(l)} = f(u_{j}^{(l)})$

平方损失函数层

$E^{(n)}=\frac{1}{2}\begin{Vmatrix} f(u^{(l)})-t \end{Vmatrix}^{2}$

可以被解构为两层

激活层： $y_{k}^{(l)}=f(u_{k}^{(l)})$ f 可以是任意函数

损失层： $E^{(n)}=\frac{1}{2}\begin{Vmatrix} y^{(l)}-t \end{Vmatrix}^{2}$

平方损失函数需要哪些层来实现?

FC layer + activation layer + Euclidean loss layer (全连接 + 激活 + 欧式距离损失)

交叉熵损失层

$E^{(n)} = -\sum_{k=1}^{k}t_{k}lnf(u_{k}^{(l)})$

可以被解构为两层

Softmax层： $y_{k}^{(L)} = f(u_{k}^{(L)})$ f 是Softmax函数

损失层： $E^{(n)} = -\sum_{k=1}^{k}t_{k}lny_{k}^{(L)}$ 不过并不必要

平方损失函数需要哪些层来实现?

FC layer + softmax cross-entropy layer (全连接 + softmax交叉熵损失)

例子1

带隐含层的多层感知机，使用平方误差损失。

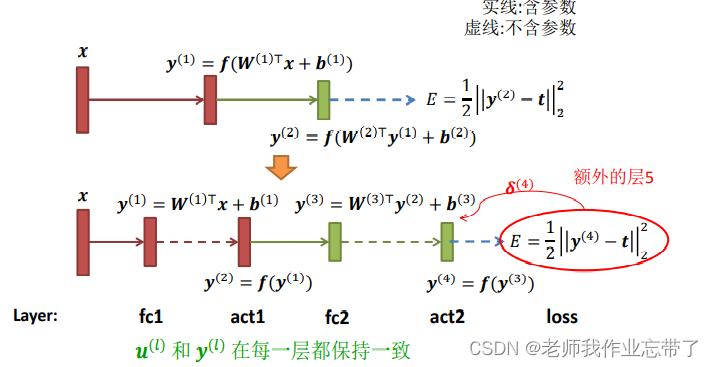
例子2

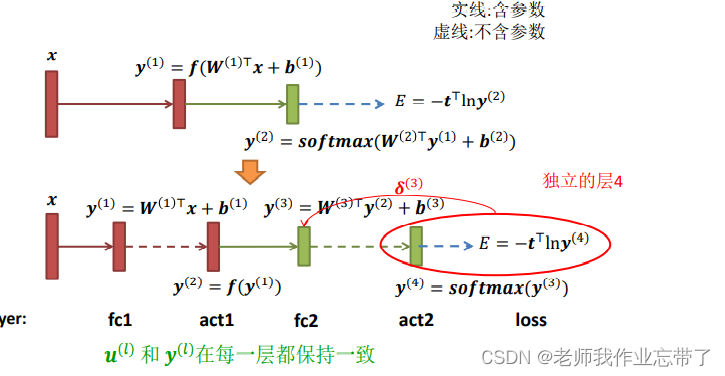
练习

**参考答案 **

向量形式的反向传播

2.5 训练技巧

初始化参数

𝑊 可以从某个分布中采样:

高斯分布(Gaussian) - 均值为零，标准差固定(例如0.01)的高斯分布
Xavier - 均值为零，标准差固定为 1/ 𝑛in 的一种分布, 其中 𝑛in 是当前神经元输入的个数- 通常使用高斯分布或均匀分布
MSRA - 均值为零，标准差固定为 2/ 𝑛in 的高斯分布

学习率

随机梯度下降中的学习率𝛼 通常远小于批量梯度下降中的，因为更新过程中存在更大的方差。

选择合适的策略

一个标准的做法是选择一个足够小的学习率使得网络开始稳定收敛，在收敛速度变慢后将学习率减半。
另一种更好的策略是每一轮训练后都在一组留出数据集(held out set) 上评估模型，如果相邻两轮训练中目标函数的改变量小于某个阈值，则减小学习率。
另一种常用策略是在第t次迭代(iteration)中将学习率修改为 𝑎/𝑏+𝑡 ，其中a是初始的学习率，b控制学习率何时开始衰减。

训练样本的顺序

如果样本的训练顺序固定，梯度的计算可能会有偏差，并导致收敛情况变差。

通常在每轮训练前都要随机打乱(random shuffle)数据集。

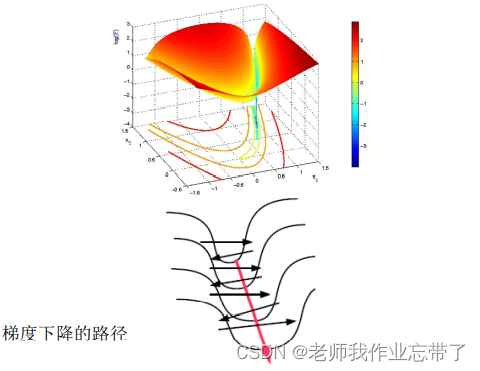
病态的曲率(Pathological Curvature)

目标函数的形式通常是狭长且浅的沟壑，就像 Rosenbrock 函数一样。

在深度网络中，目标函数的局部最优点经常以这种形式呈现，所以标准的随机梯度下降算法。通常会在“沟壑”两侧反复震荡。

$f(x,y)=(1-x)^{2}+100(y-x^{2})^{2}$

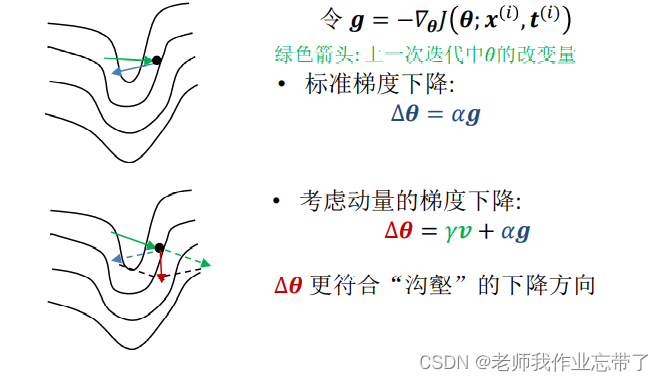
动量(Momentum)

动量(Momentum)是一种迫使目标函数沿着“沟壑”快速下降的方法。

动量的更新过程: $v=\gamma v-\alpha \triangledown _{\theta }J(\theta;x^{(i)},t^{(i)}), \: \: \: \theta =\theta +v$

𝒗 是当前的速度向量。
𝛾 ∈ (0,1] 决定了之前迭代的梯度以多大程度参与到当前的更新中。
一种策略: 𝛾 设为 0.5 直到收敛开始稳定，然后增大到0.9或更大。

例如：

三、总结

多层感知机 - 前向计算- 后向计算: 反向传播
层分解 - 全连接层, sigmoid层, ReLU层, 损失函数层
训练技巧-1 - 参数初始化, 学习率, 训练样本顺序, 动量

标签：人工智能深度学习

本文转载自: https://blog.csdn.net/suic009/article/details/125954458
版权归原作者 老师我作业忘带了 所有，如有侵权，请联系我们删除。